Inverse Trigonometric Functions 4 7 The Inverse Sine


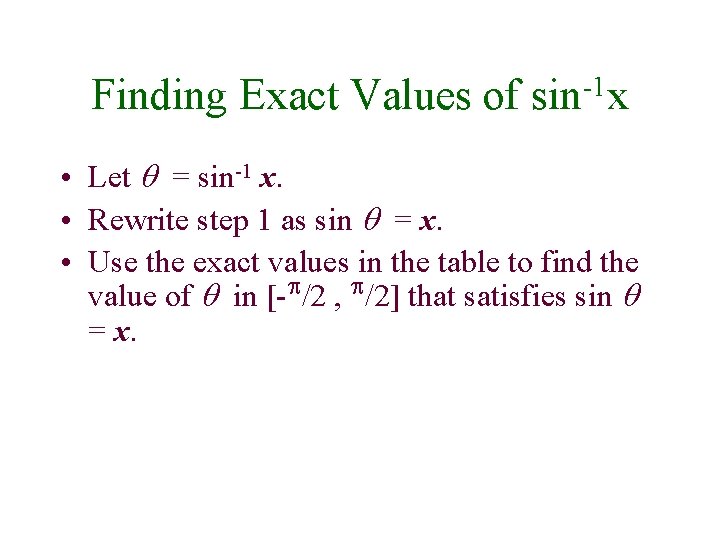
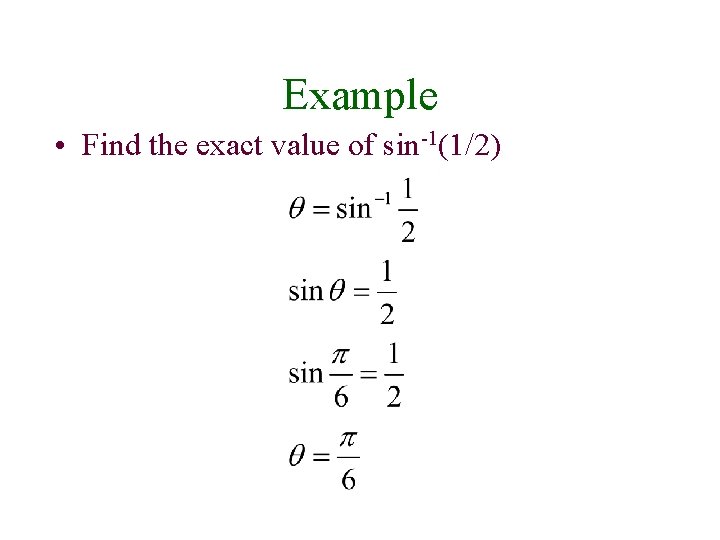














- Slides: 20

Inverse Trigonometric Functions 4. 7

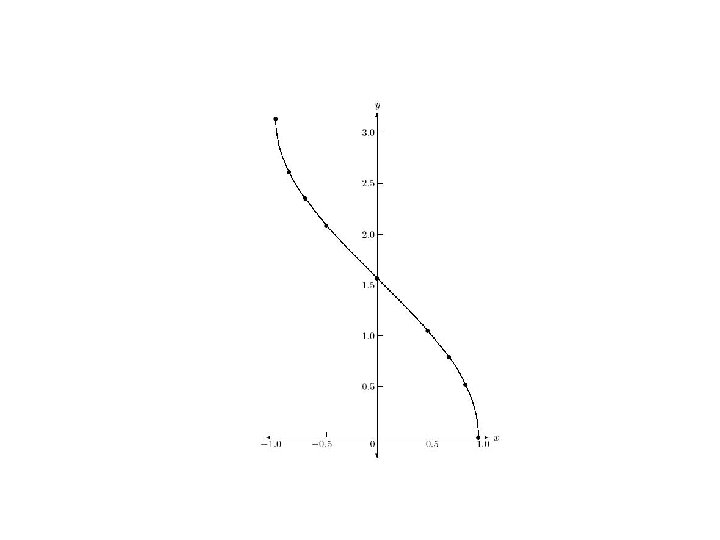
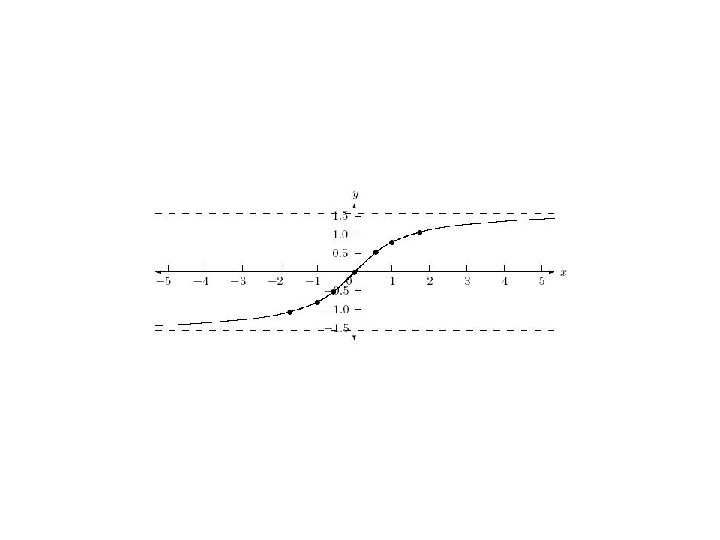
The Inverse Sine Function The inverse sine function, denoted by sin-1, is the inverse of the restricted sine function y = sin x, - /2 < x < / 2. Thus, y = sin-1 x means sin y = x, where - /2 < y < /2 and – 1 < x < 1. We read y = sin-1 x as “ y equals the inverse sine at x. ” y y = sin x - /2 < x < /2 1 - /2 -1 x Domain: [- /2, /2] Range: [-1, 1]
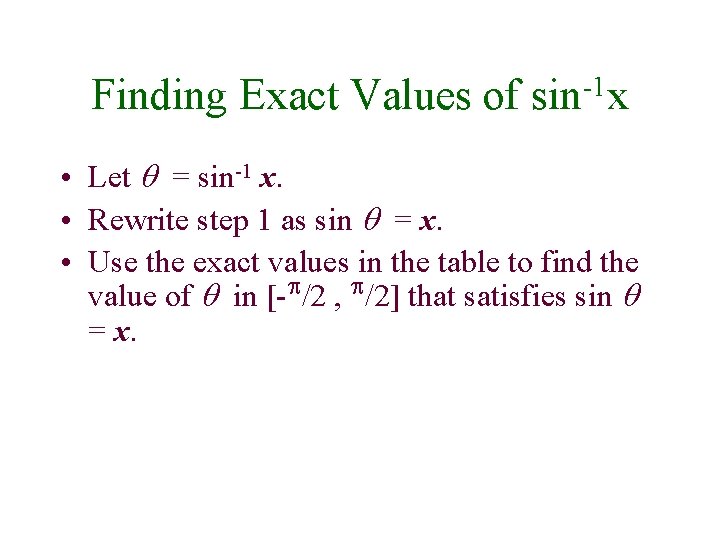
Finding Exact Values of -1 sin x • Let = sin-1 x. • Rewrite step 1 as sin = x. • Use the exact values in the table to find the value of in [- /2 , /2] that satisfies sin = x.
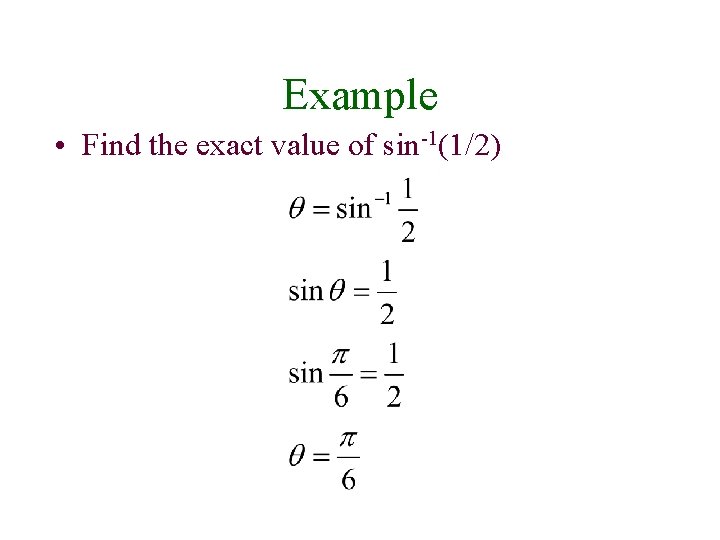
Example • Find the exact value of sin-1(1/2)

Example • Find the exact value of sin-1(-1/2)

The Inverse Cosine Function The inverse cosine function, denoted by cos-1, is the inverse of the restricted cosine function y = cos x, 0 < x < . Thus, y = cos-1 x means cos y = x, where 0 < y < and – 1 < x < 1.


Text Example Find the exact value of cos-1 (- 3 /2)

Text Example Find the exact value of cos-1 ( 2 /2)

The Inverse Tangent Function The inverse tangent function, denoted by tan -1, is the inverse of the restricted tangent function y = tan x, - /2 < x < /2. Thus, y = tan-1 x means tan y = x, where - /2 < y < /2 and – < x < .


Text Example Find the exact value of tan-1 (-1)

Text Example Find the exact value of tan-1 ( 3)

Inverse Properties The Sine Function and Its Inverse sin (sin-1 x) = x for every x in the interval [-1, 1]. sin-1(sin x) = x for every x in the interval [- /2, /2]. The Cosine Function and Its Inverse cos (cos-1 x) = x for every x in the interval [-1, 1]. cos-1(cos x) = x for every x in the interval [0, ]. The Tangent Function and Its Inverse tan (tan-1 x) = x for every real number x tan-1(tan x) = x for every x in the interval (- /2, /2).

Example

Example

Example

Example

Using you Calculator Find the angle in radians to the nearest thousandth. Then find the angle in degree.

Example • The following formula gives the viewing angle θ, in radians, for a camera whose lens is x millimeters wide. Find the viewing angle in radians and degrees for a 28 millimeter lens.
 Inverse circular functions and trigonometric equations
Inverse circular functions and trigonometric equations Summary of inverse trigonometric functions
Summary of inverse trigonometric functions 4-6 practice inverse trigonometric functions
4-6 practice inverse trigonometric functions Exponential rule integral
Exponential rule integral Inverse trigonometry range and domain
Inverse trigonometry range and domain Trig differentiation
Trig differentiation Properties of inverse trig functions
Properties of inverse trig functions Integration of inverse trigonometric functions
Integration of inverse trigonometric functions Laplace transform
Laplace transform Cot trig ratio
Cot trig ratio Lex stricta
Lex stricta Nulla poena sine lege
Nulla poena sine lege Injuria sine damno and damnum sine injuria difference
Injuria sine damno and damnum sine injuria difference What quadrants can inverse cosine be in
What quadrants can inverse cosine be in Hyperbolic functions derivatives
Hyperbolic functions derivatives Sin^-1(4/7)
Sin^-1(4/7) Range of inverse sine function
Range of inverse sine function Make cos c the subject of the formula
Make cos c the subject of the formula Trig ratios
Trig ratios 4-5 practice graphing other trigonometric functions
4-5 practice graphing other trigonometric functions Six trigonometric functions of special angles
Six trigonometric functions of special angles