6 Inverse Circular Functions and Trigonometric Equations Copyright

6 Inverse Circular Functions and Trigonometric Equations Copyright © 2013, 2009, 2005 Pearson Education, Inc. 1

Inverse Circular Functions 6 and Trigonometric Equations 6. 1 Inverse Circular Functions 6. 2 Trigonometric Equations I 6. 3 Trigonometric Equations II 6. 4 Equations Involving Inverse Trigonometric Functions Copyright © 2013, 2009, 2005 Pearson Education, Inc. 2

6. 4 Equations Involving Inverse Trigonometric Functions Solving for x in Terms of y Using Inverse Functions ▪ Solving Inverse Trigonometric Equations Copyright © 2013, 2009, 2005 Pearson Education, Inc. 3

Example 1 SOLVING AN EQUATION FOR A SPECIFIED VARIABLE Solve y = 3 cos 2 x for x, where x is restricted to the interval Divide by 3. Definition of arccosine Multiply by Because y = 3 cos 2 x for x has period π, the restriction ensures that this function is one-to-one and has a one-to-one relationship. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 4

Example 2 SOLVING AN EQUATION INVOLVING AN INVERSE TRIGONOMETRIC FUNCTION Divide by 2. Definition of arcsine CHECK Solution set: {1} Copyright © 2013, 2009, 2005 Pearson Education, Inc. 5

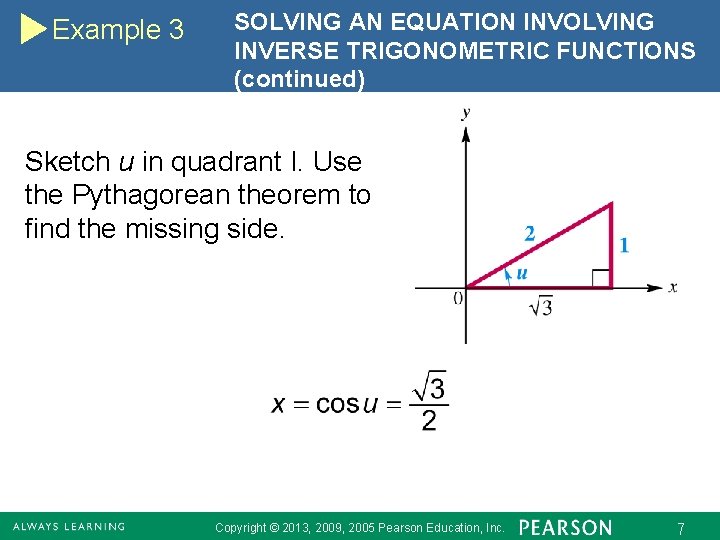
Example 3 SOLVING AN EQUATION INVOLVING INVERSE TRIGONOMETRIC FUNCTIONS and for u in quadrant I, Substitute. Definition of arccosine Copyright © 2013, 2009, 2005 Pearson Education, Inc. 6

Example 3 SOLVING AN EQUATION INVOLVING INVERSE TRIGONOMETRIC FUNCTIONS (continued) Sketch u in quadrant I. Use the Pythagorean theorem to find the missing side. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 7

Example 4 SOLVING AN INVERSE TRIGONOMETRIC EQUATION USING AN IDENTITY Isolate one inverse function on one side of the equation: Definition of arcsine The arccosine function yields angles in quadrants I and II, so, by definition, Copyright © 2013, 2009, 2005 Pearson Education, Inc. 8

Example 4 SOLVING AN INVERSE TRIGONOMETRIC EQUATION USING AN IDENTITY (cont. ) Sine sum identity From equation (1) and by the definition of the arcsine function, and u lies in quadrant I. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 9

Example 4 SOLVING AN INVERSE TRIGONOMETRIC EQUATION USING AN IDENTITY (cont. ) From the triangle, we have Substitute. Multiply by 2. Subtract x. Square each side. Distribute, then add 3 x 2. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 10

Example 4 SOLVING AN INVERSE TRIGONOMETRIC EQUATION USING AN IDENTITY (cont. ) Divide by 4. Take the square root of each side. Choose the positive root because x > 0. Now check the solution in the original equation. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 11