Inverse Functions and Inverse Trigonometric Functions Extension Content










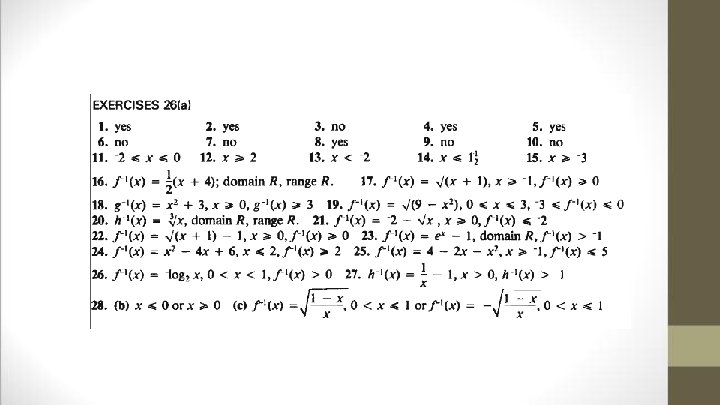


















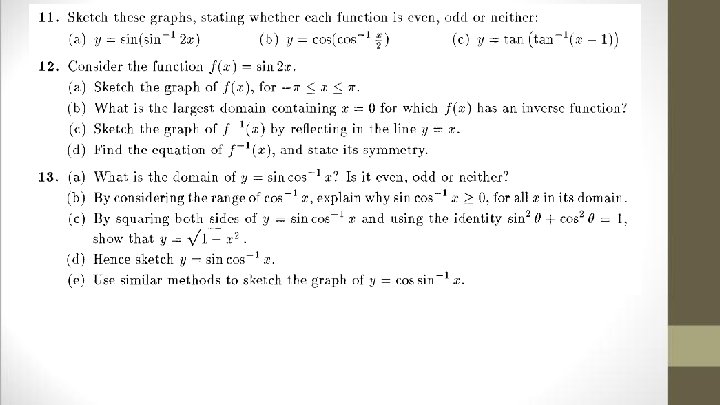





















- Slides: 59

Inverse Functions and Inverse Trigonometric Functions Extension Content

By the end of this unit: ● Have an understanding of inverse functions, how to find and manipulate them ● Be able to differentiate and integrate inverse functions, in particular recognise and use the standard integrals correctly. Make sure you complete some of the more challenging Fitzpatrick/Cambridge questions ● Make your summary including graphs ● attempt HSC questions on this topic under timed conditions

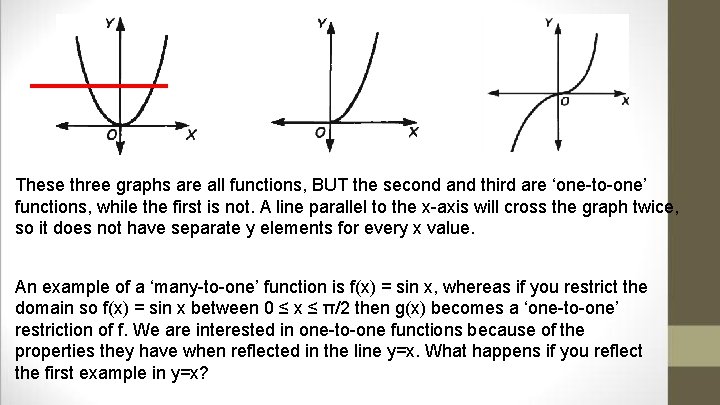
These three graphs are all functions, BUT the second and third are ‘one-to-one’ functions, while the first is not. A line parallel to the x-axis will cross the graph twice, so it does not have separate y elements for every x value. An example of a ‘many-to-one’ function is f(x) = sin x, whereas if you restrict the domain so f(x) = sin x between 0 ≤ x ≤ π/2 then g(x) becomes a ‘one-to-one’ restriction of f. We are interested in one-to-one functions because of the properties they have when reflected in the line y=x. What happens if you reflect the first example in y=x?

The necessary and sufficient condition for the reflection of f in y=x to be the graph of a function is that f is one-to-one. Inverse functions are formed by taking the ‘inverse operation’ or ‘undoing’ the operation of the function. however, the inverse is not always a function.






Groves

Fitzpatrick

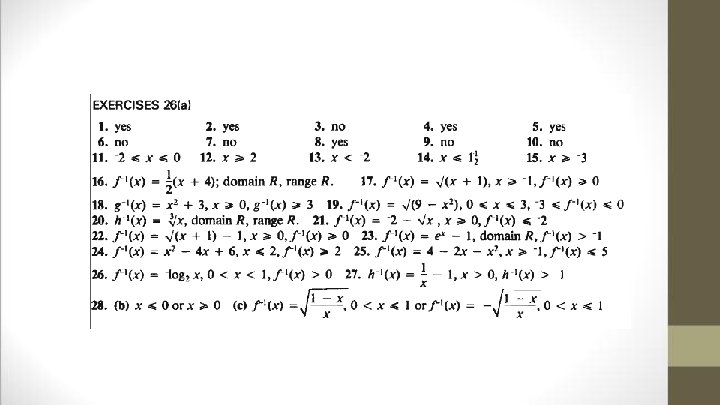

Notation: Given a function y = f(x), the inverse function is written as y = f-1(x). Sometimes it is also written as simply f-1.



Groves


Mutually Inverse Functions A function and its inverse are mutually inverse functions. That is:

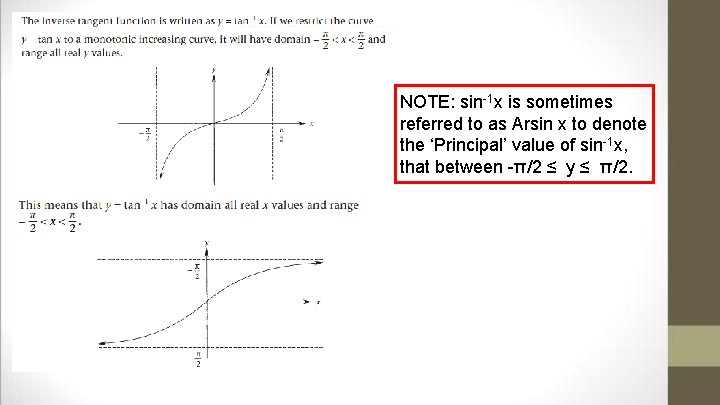
Inverse Trigonometric Functions In order for a trigonometric function to have an inverse, the function MUST have a restricted domain. For example: the inverse sine function is written as y = sin-1 x. If we restrict the curve y = sin x to a monotonic increasing curve, it will have domain -π/2 ≤ x ≤ π/2 and domain -1 ≤ y ≤ 1. This means that y = sin-1 x has domain -1 ≤ x ≤ 1 and range -π/2 ≤ y ≤ π/2. On the left is the restricted cosine curve, and y = cos-1 x on the right. What are the domain and range for each?

NOTE: sin-1 x is sometimes referred to as Arsin x to denote the ‘Principal’ value of sin-1 x, that between -π/2 ≤ y ≤ π/2.


Properties of Inverse Trig Functions


General Solution of Trigonometric Equations

Groves




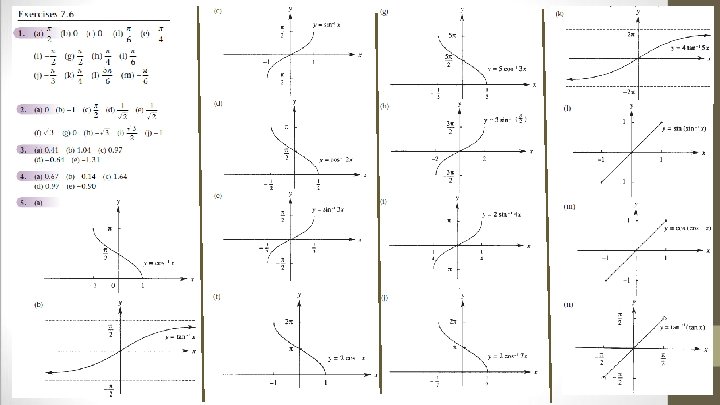
Fitzpatrick



Cambridge

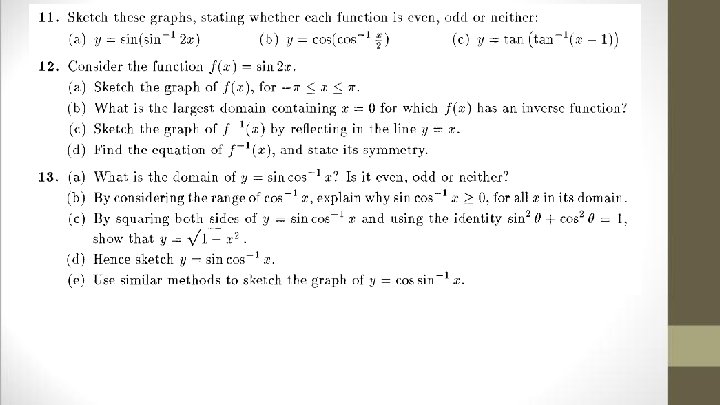




Differentiating Inverse Trigonometric Functions


2


Groves



Fitzpatrick



Cambridge



Integrating Trigonometric Functions Considering the fact that integration and differentiation are opposite processes:


Groves



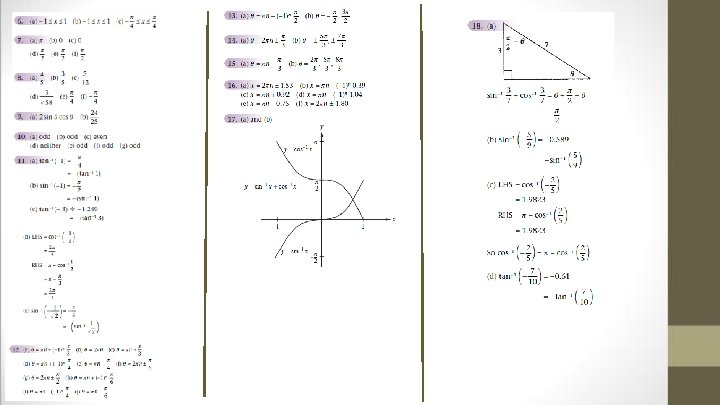
Fitzpatrick


 Inverse circular functions and trigonometric equations
Inverse circular functions and trigonometric equations Trig function
Trig function 4-6 practice inverse trigonometric functions
4-6 practice inverse trigonometric functions Derivatives of sin inverse x
Derivatives of sin inverse x Integration of inverse trigonometric functions
Integration of inverse trigonometric functions Basic integral rules
Basic integral rules Domain of the inverse cosine function
Domain of the inverse cosine function Convolution laplace transform
Convolution laplace transform Summary of inverse trigonometric functions
Summary of inverse trigonometric functions Brand leveraging strategies
Brand leveraging strategies Carrier content and real content in esp
Carrier content and real content in esp Inverse trig function calculator
Inverse trig function calculator Dynamic content vs static content
Dynamic content vs static content Domain and range of trigonometric function
Domain and range of trigonometric function Trigonometry range and domain
Trigonometry range and domain Unit circle radians
Unit circle radians Cos90
Cos90 Three basic trigonometric functions
Three basic trigonometric functions Trig function transformations
Trig function transformations Graph sine and cosine functions
Graph sine and cosine functions 12-7 graphing trigonometric functions answers
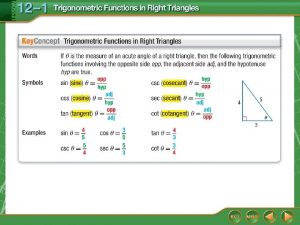
12-7 graphing trigonometric functions answers 12-1 trigonometric functions in right triangles
12-1 trigonometric functions in right triangles Differentiate trigonometric functions
Differentiate trigonometric functions Graphing sine and cosine quiz
Graphing sine and cosine quiz Limits of trigonometric functions
Limits of trigonometric functions Csc a
Csc a Parts of trigonometric functions
Parts of trigonometric functions Tan function period
Tan function period Trigonometric equations solver
Trigonometric equations solver Limit of trigonometric functions examples
Limit of trigonometric functions examples Algebra 2b unit 4
Algebra 2b unit 4 Evaluating trigonometric functions
Evaluating trigonometric functions Damped trigonometric functions
Damped trigonometric functions The six trig functions
The six trig functions General angles
General angles 12-1 trigonometric functions in right triangles
12-1 trigonometric functions in right triangles Trigonometry ratios in right triangles
Trigonometry ratios in right triangles Trigonometric functions in real life
Trigonometric functions in real life Trigonometric function transformations
Trigonometric function transformations Maximum value of trigonometric functions
Maximum value of trigonometric functions Graphing systems of linear inequalities maze answer key
Graphing systems of linear inequalities maze answer key Csc a
Csc a Six trigonometric functions of special angles
Six trigonometric functions of special angles Evaluating the six trigonometric functionsassignment
Evaluating the six trigonometric functionsassignment Chapter 4 trigonometric functions
Chapter 4 trigonometric functions Trigonometric functions
Trigonometric functions Trigonometric definitions
Trigonometric definitions Trigonometr
Trigonometr Symmetry of trigonometric functions
Symmetry of trigonometric functions Composite trigonometric functions
Composite trigonometric functions Terminal point on unit circle
Terminal point on unit circle Trigonometric functions
Trigonometric functions Chapter 5 trigonometric functions
Chapter 5 trigonometric functions Chapter 4 trigonometric functions
Chapter 4 trigonometric functions Fourier series linear algebra
Fourier series linear algebra Example of six trigonometric ratios
Example of six trigonometric ratios Trigonometric functions calculator
Trigonometric functions calculator Chapter 13 trigonometric functions answers
Chapter 13 trigonometric functions answers Differentiation of algebraic functions
Differentiation of algebraic functions Trigonometric equations formulas
Trigonometric equations formulas