Contents The inverse trigonometric functions The reciprocal trigonometric

Contents The inverse trigonometric functions The reciprocal trigonometric functions Trigonometric identities Examination-style question 1 of 35 © Boardworks Ltd 2006

The inverse of the sine function Suppose we wish to find θ such that sin θ = x In other words, we want to find the angle whose sine is x. This is written as θ = sin– 1 x or θ = arcsin x In this context, sin– 1 x means the inverse of sin x. This is not the same as (sin x)– 1 which is the reciprocal of sin x, . Is y = sin– 1 x a function?

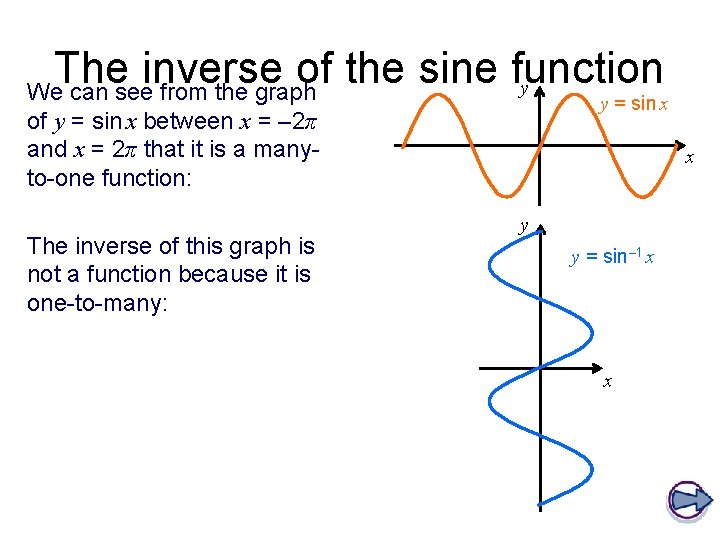
The inverse of the sine function y We can see from the graph y = sin x of y = sin x between x = – 2π and x = 2π that it is a manyto-one function: The inverse of this graph is not a function because it is one-to-many: x y y = sin– 1 x x

The inverse of the sine function However, remember that if we use a calculator to find sin x – 1 (or arcsin x) the calculator will give a value between – 90° and 90° (or between – ≤ x ≤ if working in radians). There is only one value of sin– 1 x in this range, called the principal value. So, if we restrict the domain of f(x) = sin x to – ≤ x ≤ we have a one-to-one function: y 1 y = sin x x – 1

– 1 x The graph of y = sin Therefore the inverse of f(x) = sin x, – ≤ x ≤ , is also a one-to-one function: f – 1(x) = sin– 1 x y y = sin– 1 x The graph of y = 1 is the reflection of y = sin x in the line y = x: x (Remember the scale – 1 1 – 1 used on the x- and y-axes must be the same. ) The domain of sin– 1 x is the same as the range of sin x : – 1 ≤ x ≤ 1 The range of sin– 1 x is the same as the restricted domain of sin x : – ≤ sin– 1 x ≤

The inverse of cosine and We can restrict the domains of cos x and tan x in the same way tangent as we did for sin x so that if f(x) = cos x then f – 1(x) = cos– 1 x And if f(x) = tan x then f – 1(x) = tan– 1 x for for 0≤x≤π – 1 ≤ x ≤ 1. – <x< x The graphs cos– 1 x and tan– 1 x can be obtained by reflecting the graphs of cos x and tan x in the line y = x.

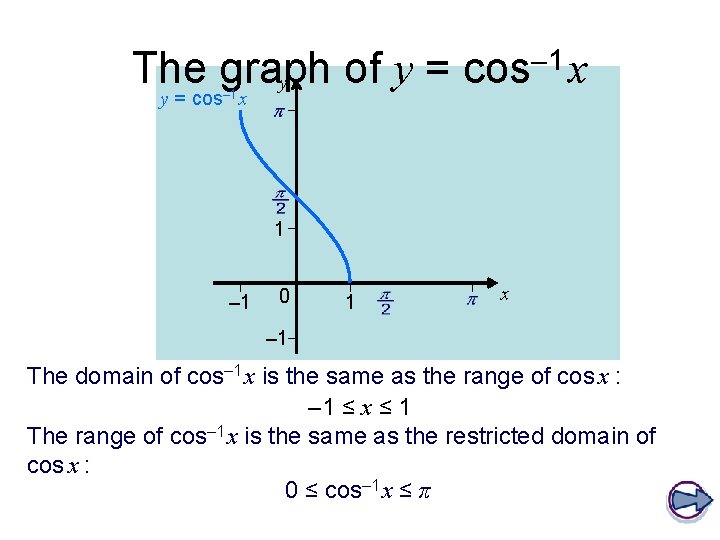
– 1 x The graph of y = cos y y = cos– 1 x 1 – 1 0 – 1 1 x y = cosx The domain of cos– 1 x is the same as the range of cos x : – 1 ≤ x ≤ 1 The range of cos– 1 x is the same as the restricted domain of cos x : 0 ≤ cos– 1 x ≤ π

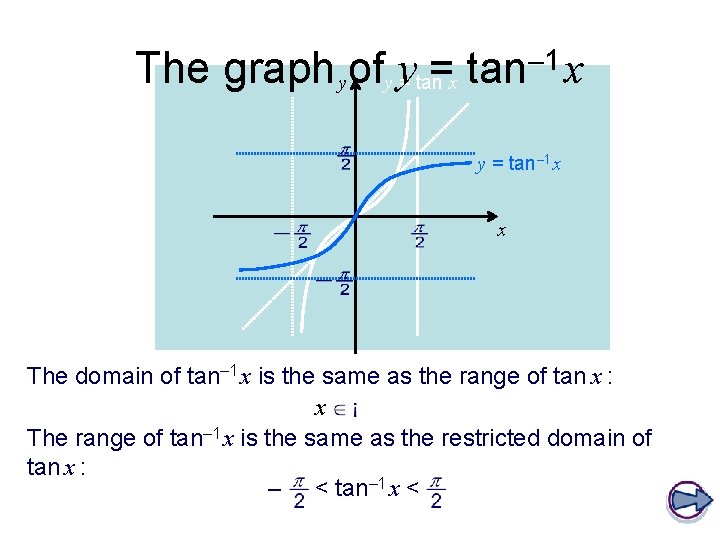
– 1 x The graph yofy y= tanx = tan x y = tan– 1 x x The domain of tan– 1 x is the same as the range of tan x : x The range of tan– 1 x is the same as the restricted domain of tan x : – < tan– 1 x <

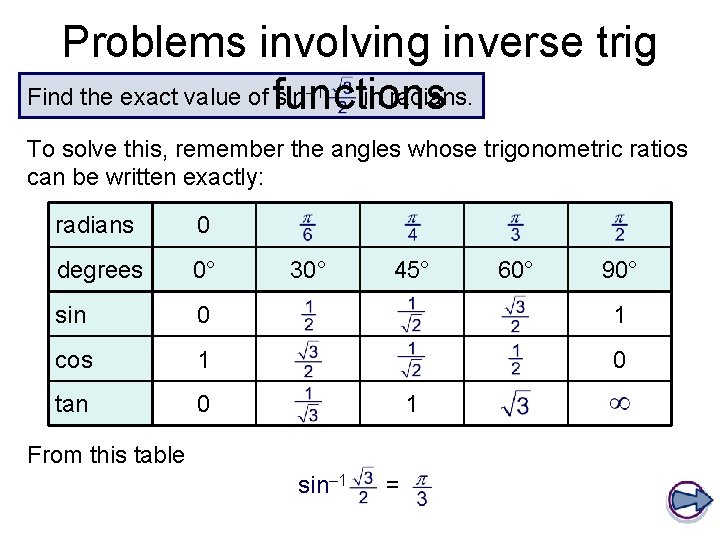
Problems involving inverse trig Find the exact value of functions sin in radians. – 1 To solve this, remember the angles whose trigonometric ratios can be written exactly: radians 0 degrees 0° sin 0 1 cos 1 0 tan 0 30° 45° 1 From this table sin– 1 = 60° 90°

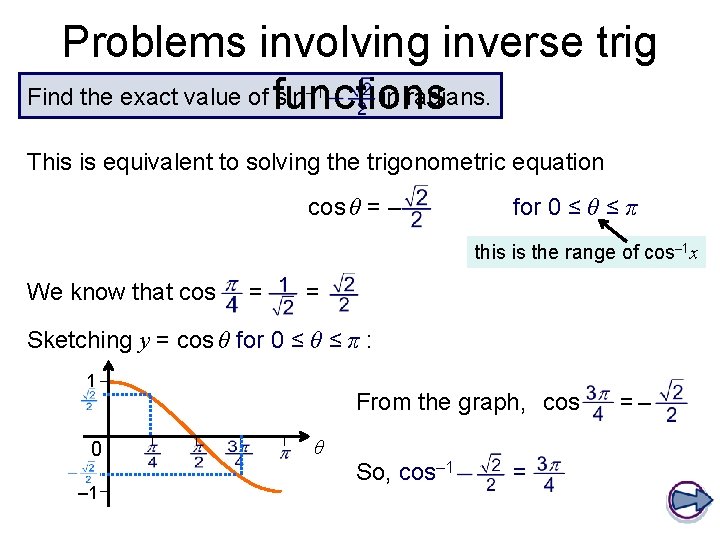
Problems involving inverse trig Find the exact value of functions sin in radians. – 1 This is equivalent to solving the trigonometric equation cos θ = – for 0 ≤ θ ≤ π this is the range of cos– 1 x We know that cos = = Sketching y = cos θ for 0 ≤ θ ≤ π : 1 0 – 1 From the graph, cos θ So, cos– 1 = =–

Problems involving inverse trig Find the exact value of functions cos (sin ) in radians. – 1 Let sin– 1 =θ so sin θ = Using the following right-angled triangle: 7 + a 2 = 16 a=3 4 θ 3 The length of the third side is 3 so cos θ = But sin– 1 = θ so cos (sin– 1 )=