4 5 Graphs of Sine and Cosine Functions










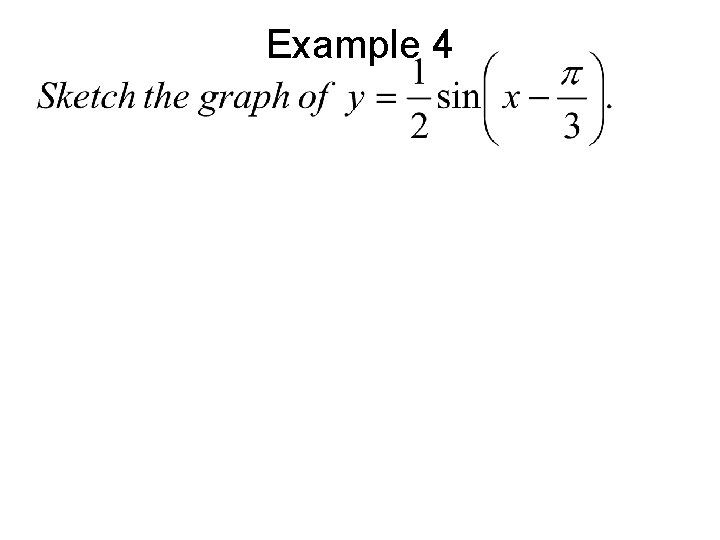




- Slides: 22

4. 5 Graphs of Sine and Cosine Functions

In this lesson you will learn to graph functions of the form y = a sin bx and y = a cos bx where a and b are positive constants and x is in radian measure. The graphs of all sine and cosine functions are related to the graphs of y = sin x and y = cos x which are shown below. y = sin x y = cos x

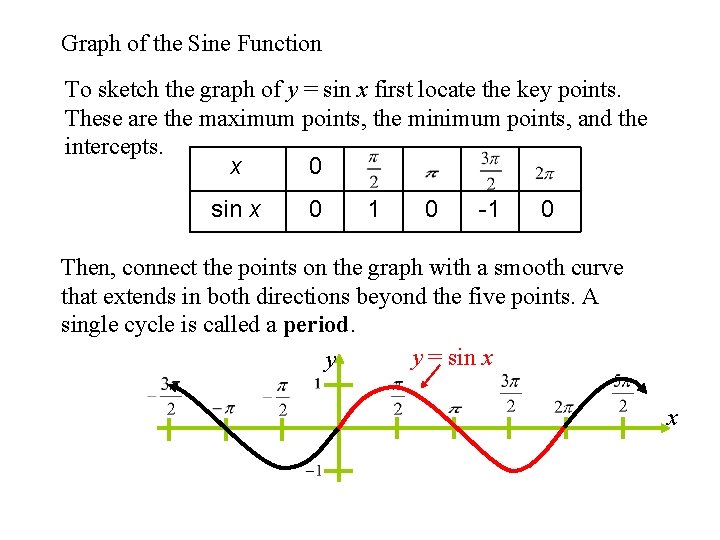
Fill in the chart. x Sin x Cos x These will be key points on the graphs of y = sin x and y = cos x.

Properties of Sine and Cosine Functions The graphs of y = sin x and y = cos x have similar properties: 1. The domain is the set of real numbers. 2. The range is the set of y values such that . 3. The maximum value is 1 and the minimum value is – 1. 4. The graph is a smooth curve. 5. Each function cycles through all the values of the range over an x-interval of. 6. The cycle repeats itself indefinitely in both directions of the x-axis.

Graph of the Sine Function To sketch the graph of y = sin x first locate the key points. These are the maximum points, the minimum points, and the intercepts. x 0 sin x 0 1 0 -1 0 Then, connect the points on the graph with a smooth curve that extends in both directions beyond the five points. A single cycle is called a period. y = sin x y x

Graph of the Cosine Function To sketch the graph of y = cos x first locate the key points. These are the maximum points, the minimum points, and the intercepts. x 0 cos x 1 0 -1 0 1 Then, connect the points on the graph with a smooth curve that extends in both directions beyond the five points. A single cycle is called a period. y = cos x y x

Before sketching a graph, you need to know: • Amplitude – Constant that gives vertical stretch or shrink. • Period – • Interval – Divide period by 4 • Critical points – You need 5. (max. , min. , intercepts. )

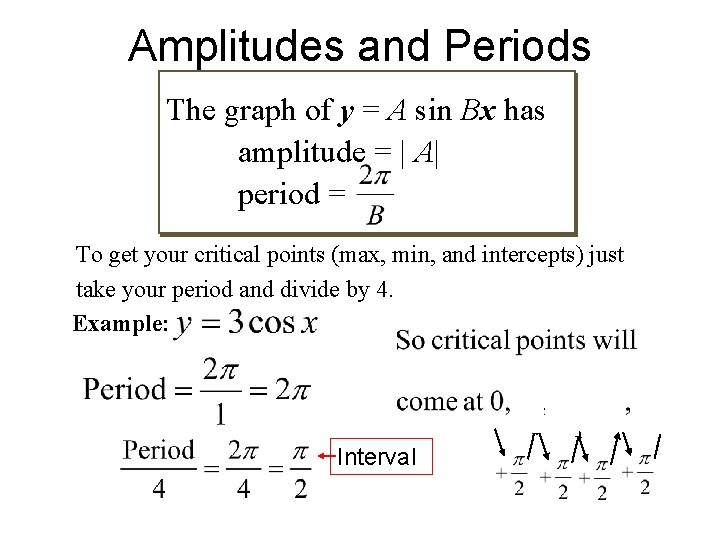
Amplitudes and Periods The graph of y = A sin Bx has amplitude = | A| period = To get your critical points (max, min, and intercepts) just take your period and divide by 4. Example: Interval

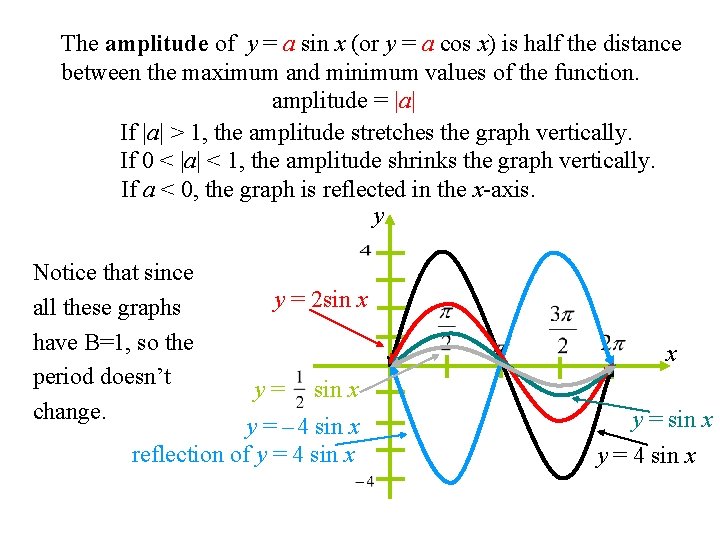
The amplitude of y = a sin x (or y = a cos x) is half the distance between the maximum and minimum values of the function. amplitude = |a| If |a| > 1, the amplitude stretches the graph vertically. If 0 < |a| < 1, the amplitude shrinks the graph vertically. If a < 0, the graph is reflected in the x-axis. y Notice that since all these graphs have B=1, so the period doesn’t change. y = 2 sin x x y= sin x y = – 4 sin x reflection of y = 4 sin x

The period of a function is the x interval needed for the function to complete one cycle. For b 0, the period of y = a sin bx is . For b 0, the period of y = a cos bx is also . If b > 1, the graph of theyfunction is shrunk horizontally. period: 2 x If 0 < b < 1, the graph of y the function is stretched horizontally. period: 4 period: 2 x

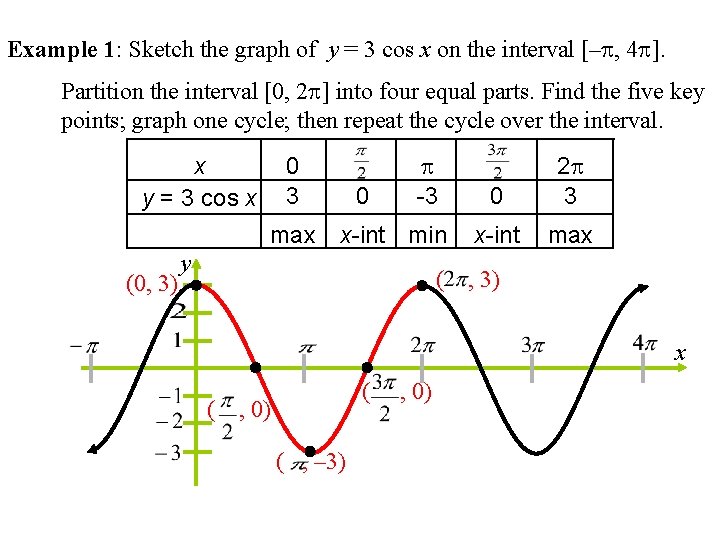
Example 1: Sketch the graph of y = 3 cos x on the interval [– , 4 ]. Partition the interval [0, 2 ] into four equal parts. Find the five key points; graph one cycle; then repeat the cycle over the interval. x y = 3 cos x 0 3 max (0, 3) 0 -3 x-int min y ( 0 2 3 x-int max , 3) x ( ( , 0) ( , – 3) , 0)

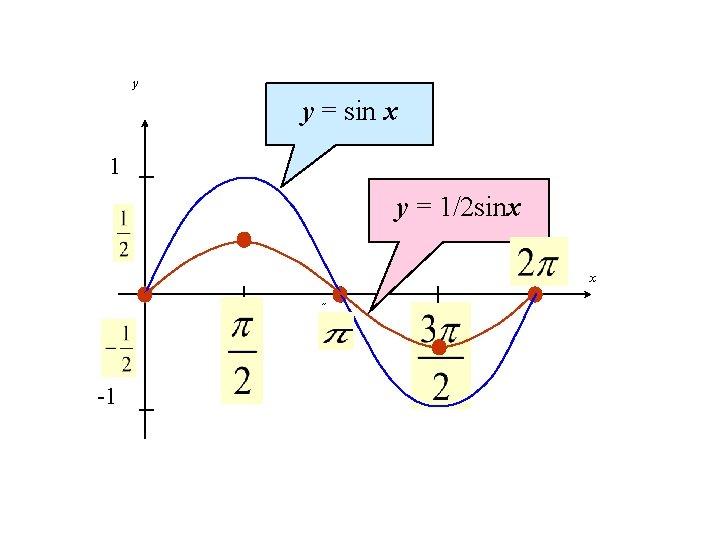
Example 2 Determine the amplitude of y = 1/2 sin x. Then graph y = sin x and y = 1/2 sin x for 0 < x < 2.

y y = sin x 1 y = 1/2 sinx 2˝ x ˝ -1

Example 3

Example 3

For the equations y = a sin(bx-c)+d and y = a cos(bx-c)+d • a represents the amplitude. This constant acts as a scaling factor – a vertical stretch or shrink of the original function. • Amplitude = • The period is the sin/cos curve making one complete cycle. • Period = • c makes a horizontal shift. • d makes a vertical shift. • The left and right endpoints of a one-cycle interval can be determined by solving the equations bx-c=0 and bx -c=
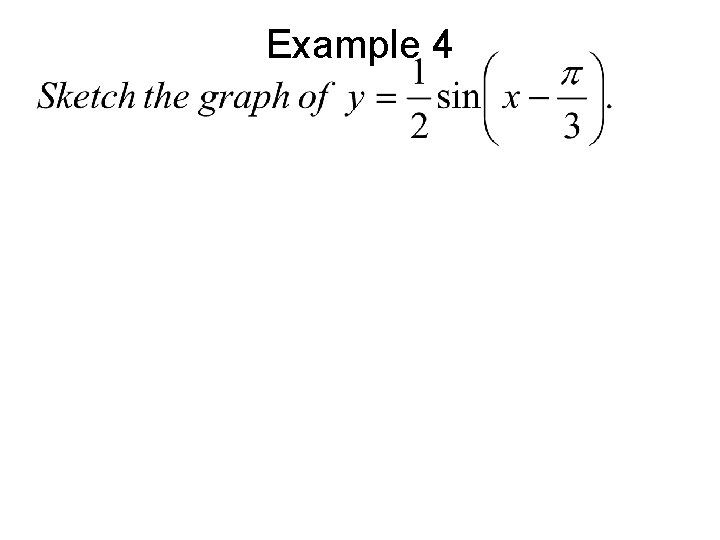
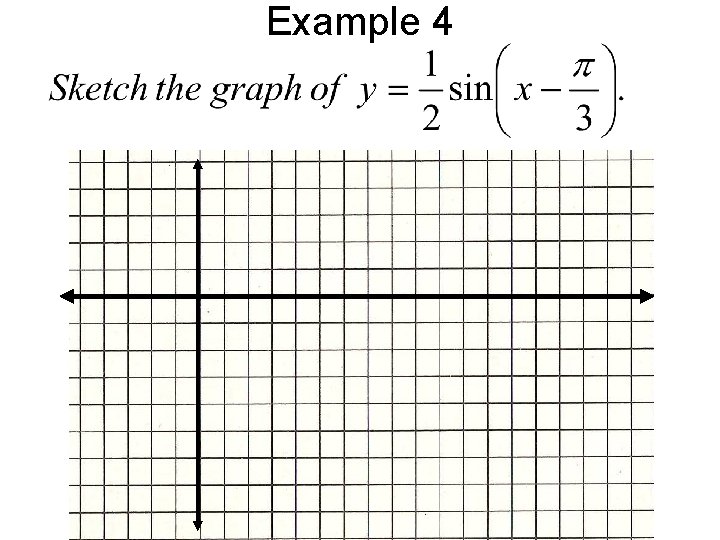
Example 4

Example 4

Example 6

Example 6

Tides • Throughout the day, the depth of the water at the end of a dock in Bangor, Washington varies with the tides. The tables shows the depths (in feet) at various times during the morning. (a) Use a trig function to model the data. (b) A boat needs at least 10 feet of water to moor at the dock. During what times in the evening can it safely dock? Time Midnight 2 a. m. 4 a. m 6 a. m. 8 a. m. 10 a. m. Noon Depth, y 3. 1 7. 8 11. 3 10. 9 6. 6 1. 7 0. 9

Homework • Page 304 -305 • 3 -13 odd, 15 -21 odd, 31 – 34 all, 47 -57 odd, 65, 67
 Graph transformations
Graph transformations Period on a sine graph
Period on a sine graph 9-5 practice graphing trigonometric functions
9-5 practice graphing trigonometric functions Lesson 4-4 graphing sine and cosine functions
Lesson 4-4 graphing sine and cosine functions Graph of sine and cosine functions
Graph of sine and cosine functions Horizontal phase shift
Horizontal phase shift Transformations of sine and cosine functions
Transformations of sine and cosine functions Graph of sine and cosine functions
Graph of sine and cosine functions Graph of sine and cosine functions
Graph of sine and cosine functions Graph of sine and cosine functions
Graph of sine and cosine functions Transformations of sine and cosine functions
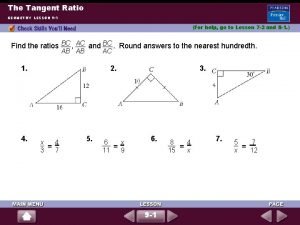
Transformations of sine and cosine functions Practice 9-2 sine and cosine ratios
Practice 9-2 sine and cosine ratios Rearrangement of cosine rule
Rearrangement of cosine rule Sine maze
Sine maze Sohcahtoa rule
Sohcahtoa rule What is the sine and cosine rule
What is the sine and cosine rule Value of tan inverse
Value of tan inverse Sine cosine rule
Sine cosine rule Sine cosine tangent word problems
Sine cosine tangent word problems Practice 8-4 sine and cosine ratios geometry
Practice 8-4 sine and cosine ratios geometry Burj khalifa trigonometry
Burj khalifa trigonometry Series de fourier
Series de fourier What is amplitude in trigonometry
What is amplitude in trigonometry