2 1 Graphs of Sine and Cosine Functions


































- Slides: 53

2. 1 Graphs of Sine and Cosine Functions Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 1

Learning Objectives • Understand the graph of y = sin x. • Graph variations of y = sin x. • Understand the graph of y = cos x. • Graph variations of y = cos x. • Use vertical shifts of sine and cosine curves. • Model periodic behavior. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 2

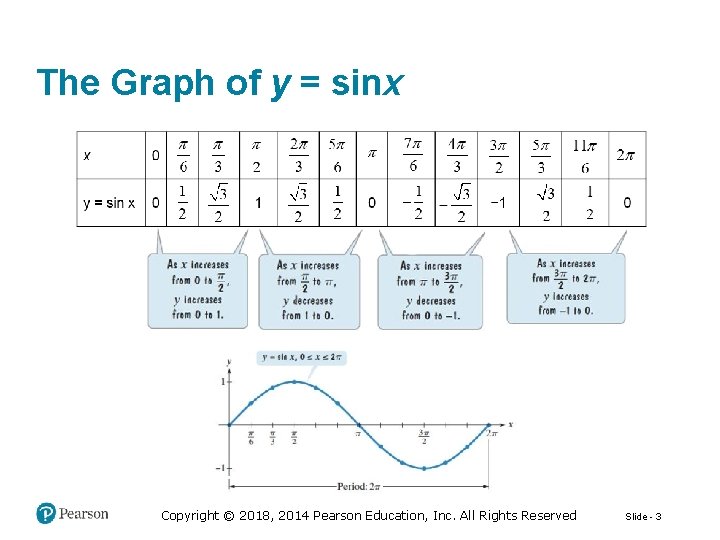
The Graph of y = sinx Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 3

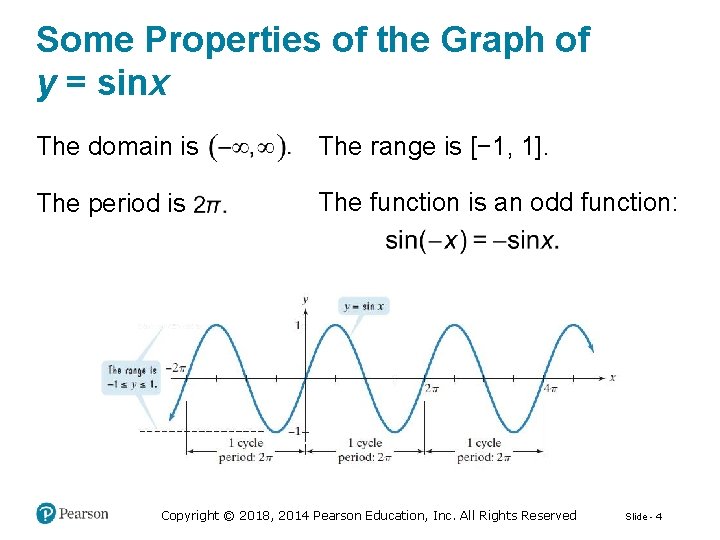
Some Properties of the Graph of y = sinx The domain is The range is [− 1, 1]. The period is The function is an odd function: Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 4

Graphing Variations of y = sinx 1. Identify the amplitude and the period. 2. Find the values of x for the five key points—the three x-intercepts, the maximum point, and the minimum point. Start with the value of x where the cycle begins and add quarter-periods—that is, —to find successive values of x. 3. Find the values of y for the five key points by evaluating the function at each value of x from step 2. 4. Connect the five key points with a smooth curve and graph one complete cycle of the given function. 5. Extend the graph in step 4 to the left or right as desired. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 5

Example 1: Graphing a Variation of y = sinx (1 of 4) Then graph Determine the amplitude of Step 1: Identify the amplitude and the period. The equation is of the form Thus, the amplitude is This means that the Maximum value of y is 3 and the minimum value of y is − 3. The period is Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 6

Example 1: Graphing a Variation of y = sinx (2 of 4) Determine the amplitude of Then graph Step 2: Find the values of x for the five key points. To generate x-values for each of the five key points, we begin by dividing the period, by 4. The cycle begins at x 1 = 0. We add quarter periods to generate x-values for each of the key points. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 7

Example 1: Graphing a Variation of y = sinx (3 of 4) Step 3: Find the values of y for the five key points. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 8

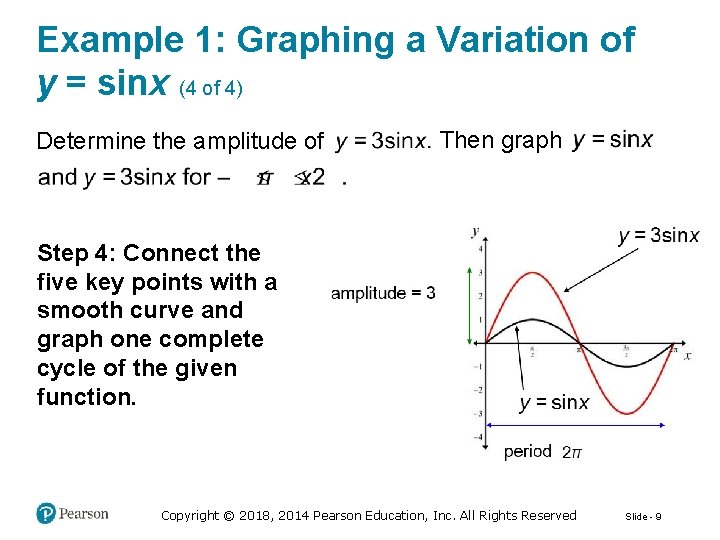
Example 1: Graphing a Variation of y = sinx (4 of 4) Determine the amplitude of Then graph Step 4: Connect the five key points with a smooth curve and graph one complete cycle of the given function. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 9

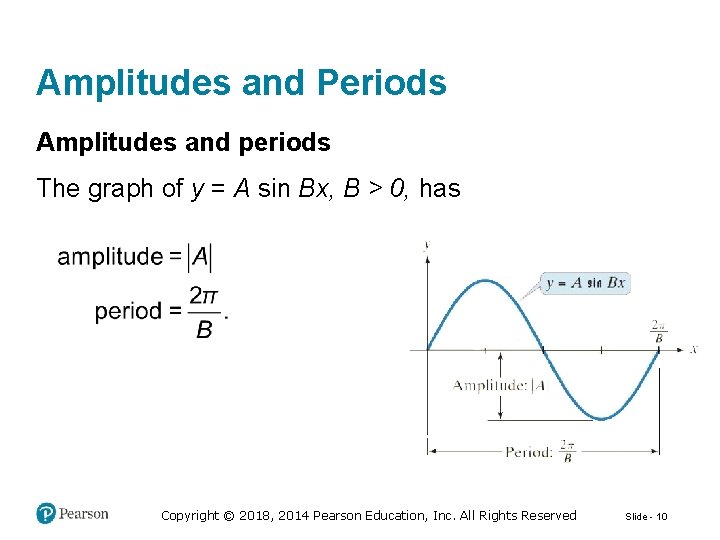
Amplitudes and Periods Amplitudes and periods The graph of y = A sin Bx, B > 0, has Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 10

Example 2: Graphing a Function of the Form y = Asin. Bx (1 of 5) Determine the amplitude and period of Then graph the function for Step 1: Identify the amplitude and the period. The equation is of the form y = A sin. Bx with A = 2 and The maximum value of y is 2, the minimum value of y is − 2. the period of tells us that the graph completes one cycle from 0 to Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 11

Example 2: Graphing a Function of the Form y = Asin. Bx (2 of 5) Step 2: Find the values of x for the five key points. To generate x-values for each of the five key points, we begin by dividing the period, by 4. The cycle begins at x 1 = 0. We add quarter periods to generate x-values for each of the key points. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 12

Example 2: Graphing a Function of the Form y = Asin. Bx (3 of 5) Step 3: Find the values of y for the five key points. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 13

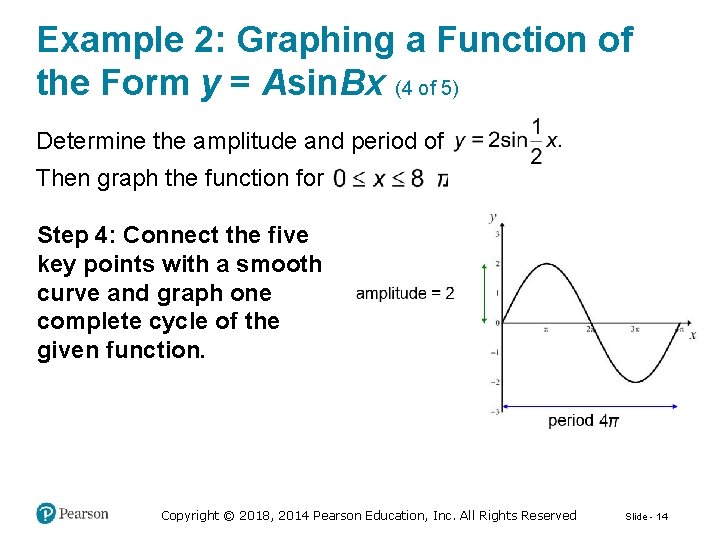
Example 2: Graphing a Function of the Form y = Asin. Bx (4 of 5) Determine the amplitude and period of Then graph the function for Step 4: Connect the five key points with a smooth curve and graph one complete cycle of the given function. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 14

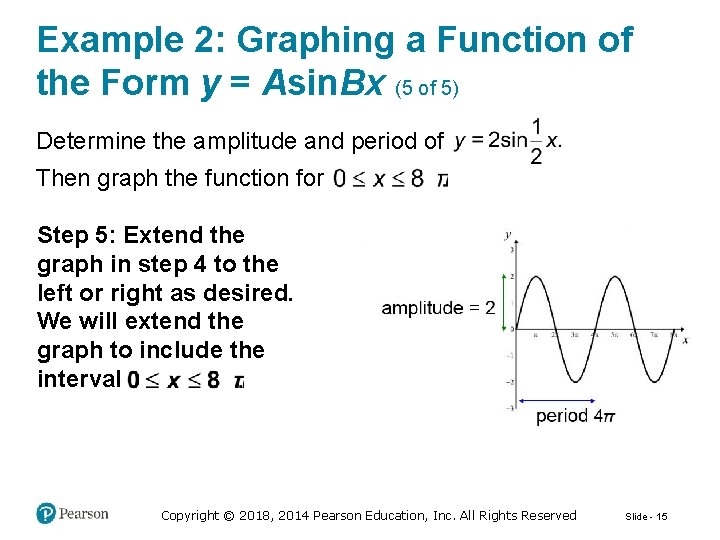
Example 2: Graphing a Function of the Form y = Asin. Bx (5 of 5) Determine the amplitude and period of Then graph the function for Step 5: Extend the graph in step 4 to the left or right as desired. We will extend the graph to include the interval Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 15

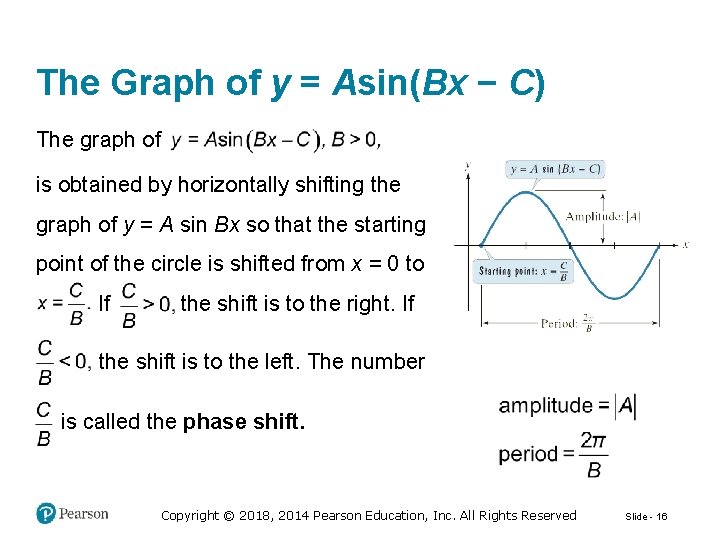
The Graph of y = Asin(Bx − C) The graph of is obtained by horizontally shifting the graph of y = A sin Bx so that the starting point of the circle is shifted from x = 0 to If the shift is to the right. If the shift is to the left. The number is called the phase shift. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 16

Example 3: Graphing a Function of the Form y = Asin(Bx − C) (1 of 5) Determine the amplitude, period, and phase shift of Then graph one period of the function. Step 1: Identify the amplitude, the period, and the phase shift. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 17

Example 3: Graphing a Function of the Form y = Asin(Bx − C) (2 of 5) Step 2: Find the values of x for the five key points. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 18

Example 3: Graphing a Function of the Form y = Asin(Bx − C) (3 of 5) Step 3: Find the values of y for the five key points. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 19

Example 3: Graphing a Function of the Form y = Asin(Bx − C) (4 of 5) Step 3: Find the values of y for the five key points. [continued] Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 20

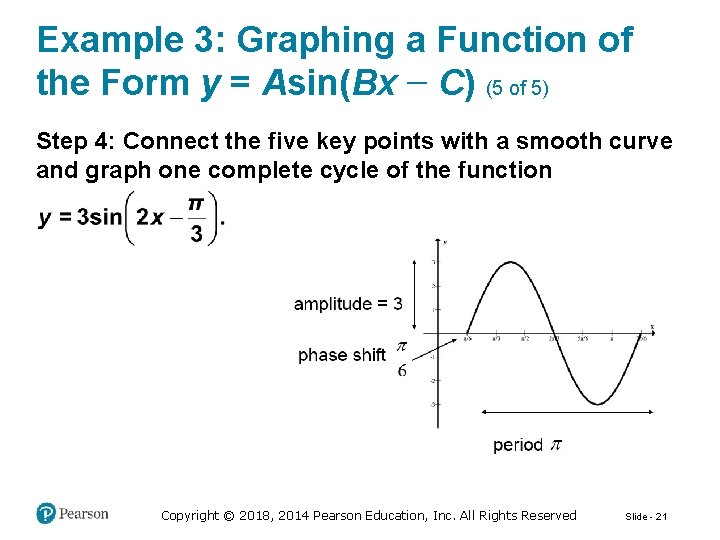
Example 3: Graphing a Function of the Form y = Asin(Bx − C) (5 of 5) Step 4: Connect the five key points with a smooth curve and graph one complete cycle of the function Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 21

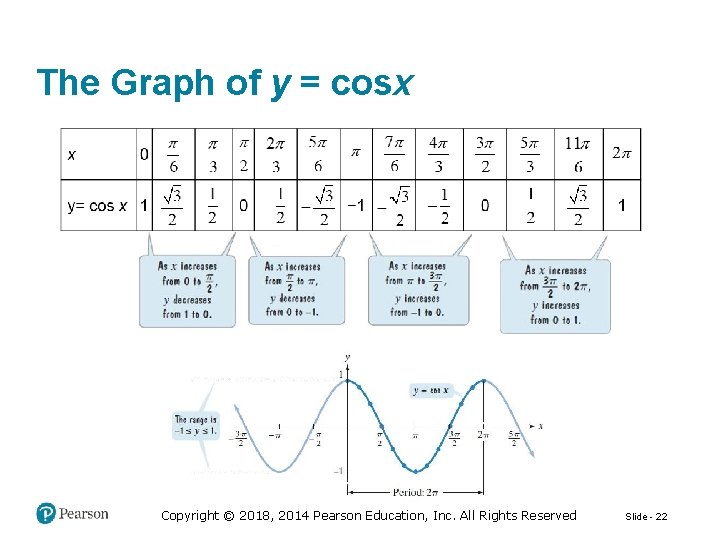
The Graph of y = cosx Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 22

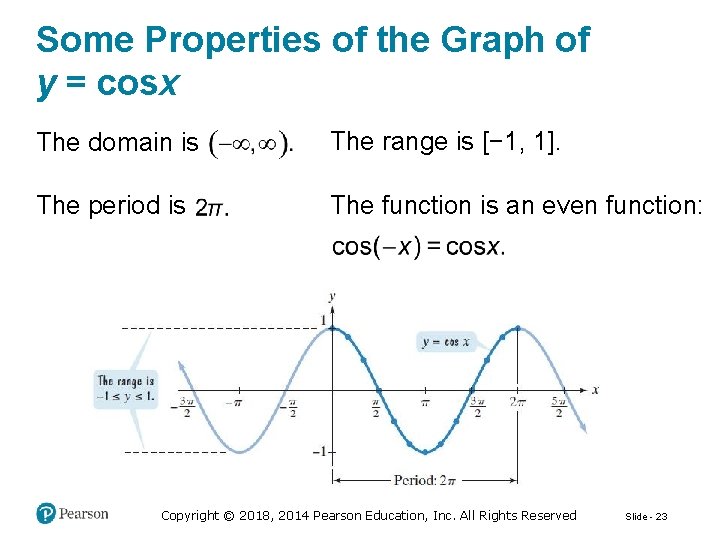
Some Properties of the Graph of y = cosx The domain is The range is [− 1, 1]. The period is The function is an even function: Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 23

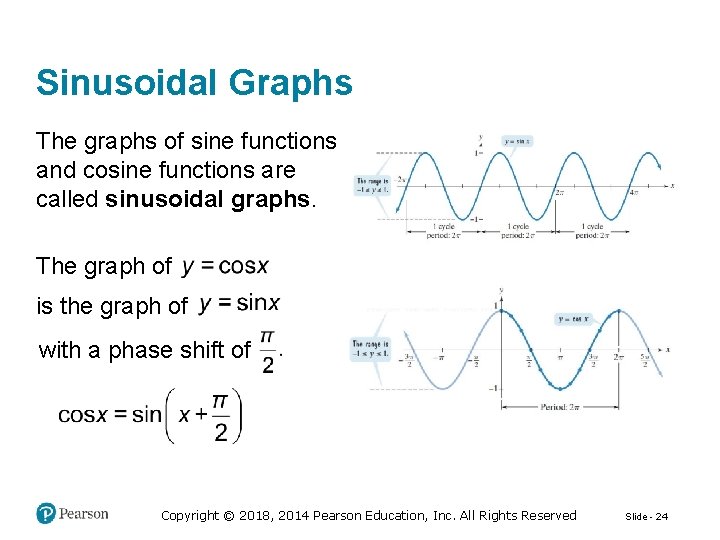
Sinusoidal Graphs The graphs of sine functions and cosine functions are called sinusoidal graphs. The graph of is the graph of with a phase shift of Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 24

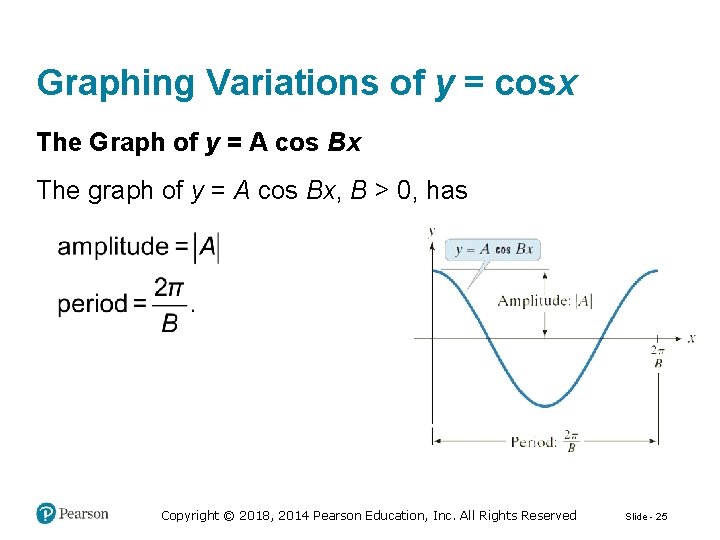
Graphing Variations of y = cosx The Graph of y = A cos Bx The graph of y = A cos Bx, B > 0, has Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 25

Example 4: Graphing a Function of the Form y = Acos. Bx (1 of 6) Determine the amplitude and period of Then graph the function for Step 1: Identify the amplitude and the period. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 26

Example 4: Graphing a Function of the Form y = Acos. Bx (2 of 6) Determine the amplitude and period of Then graph the function for Step 2: Find the values of x for the five key points. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 27

Example 4: Graphing a Function of the Form y = Acos. Bx (3 of 6) Step 3: Find the values of y for the five key points. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 28

Example 4: Graphing a Function of the Form y = Acos. Bx (4 of 6) Step 3: Find the values of y for the five key points. [continued] Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 29

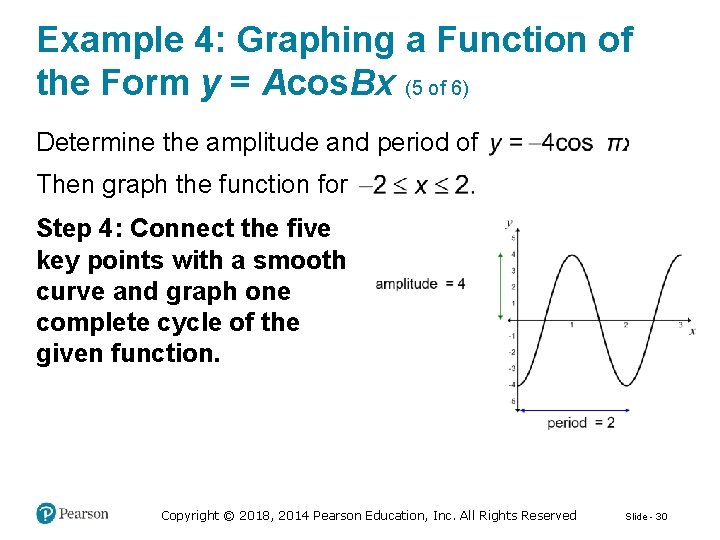
Example 4: Graphing a Function of the Form y = Acos. Bx (5 of 6) Determine the amplitude and period of Then graph the function for Step 4: Connect the five key points with a smooth curve and graph one complete cycle of the given function. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 30

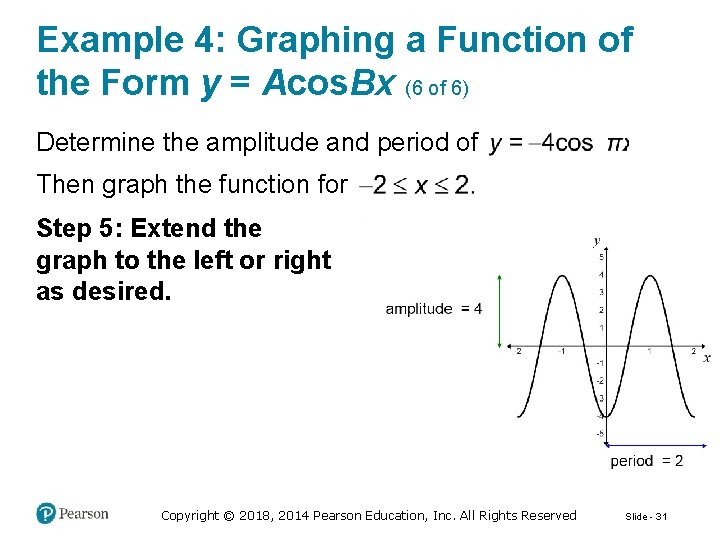
Example 4: Graphing a Function of the Form y = Acos. Bx (6 of 6) Determine the amplitude and period of Then graph the function for Step 5: Extend the graph to the left or right as desired. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 31

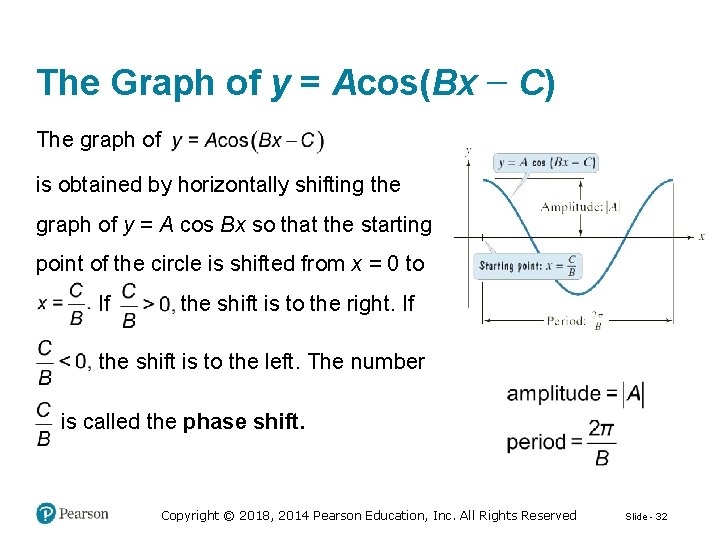
The Graph of y = Acos(Bx − C) The graph of is obtained by horizontally shifting the graph of y = A cos Bx so that the starting point of the circle is shifted from x = 0 to If the shift is to the right. If the shift is to the left. The number is called the phase shift. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 32

Example 5: Graphing a Function of the Form y = Acos(Bx − C) (1 of 6) Determine the amplitude, period, and phase shift of Then graph one period of the function. Step 1: Identify the amplitude, the period, and the phase shift. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 33

Example 5: Graphing a Function of the Form y = Acos(Bx − C) (2 of 6) Determine the amplitude, period, and phase shift of Then graph one period of the function. Step 2: Find the x-values for the five key points. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 34

Example 5: Graphing a Function of the Form y = Acos(Bx − C) (3 of 6) Step 3: Find the values of y for the five key points. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 35

Example 5: Graphing a Function of the Form y = Acos(Bx − C) (4 of 6) Step 3: Find the values of y for the five key points. [continued] Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 36

Example 5: Graphing a Function of the Form y = Acos(Bx − C) (5 of 6) Step 3: Find the values of y for the five key points. [continued] Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 37

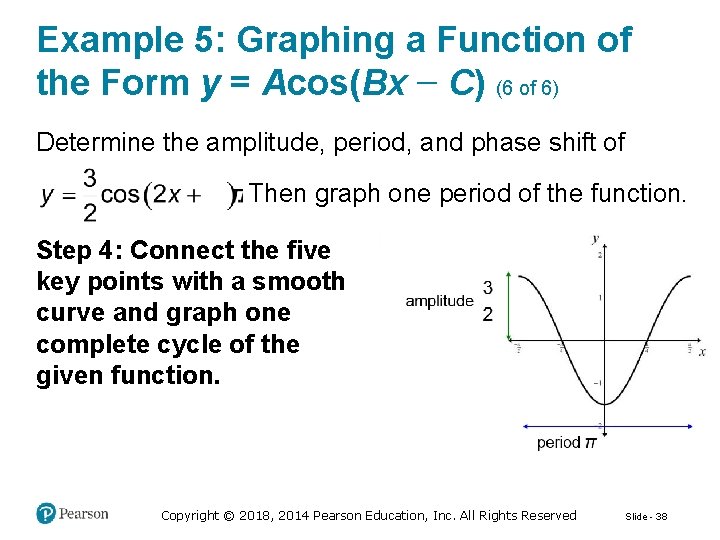
Example 5: Graphing a Function of the Form y = Acos(Bx − C) (6 of 6) Determine the amplitude, period, and phase shift of Then graph one period of the function. Step 4: Connect the five key points with a smooth curve and graph one complete cycle of the given function. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 38

Vertical Shifts of Sinusoidal Graphs For sinusoidal graphs of the form the constant D causes a vertical shift in the graph. These vertical shifts result in sinusoidal graphs oscillating about the horizontal line y = D rather than about the x-axis. The maximum value of y is The minimum value of y is Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 39

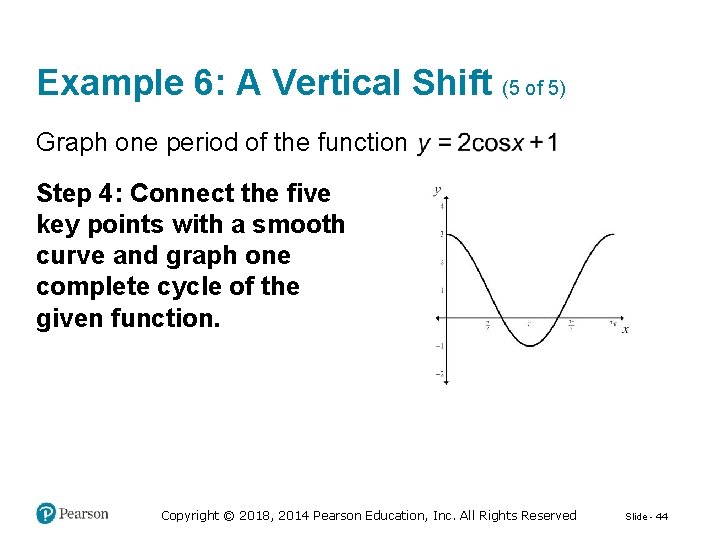
Example 6: A Vertical Shift (1 of 5) Graph one period of the function Step 1: Identify the amplitude, period, phase shift, and vertical shift. phase shift: 0 vertical shift: one unit upward Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 40

Example 6: A Vertical Shift (2 of 5) Graph one period of the function Step 2: Find the values of x for the five key points. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 41

Example 6: A Vertical Shift (3 of 5) Step 3: Find the values of y for the five key points. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 42

Example 6: A Vertical Shift (4 of 5) Step 3: Find the values of y for the five key points. [continued] Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 43

Example 6: A Vertical Shift (5 of 5) Graph one period of the function Step 4: Connect the five key points with a smooth curve and graph one complete cycle of the given function. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 44

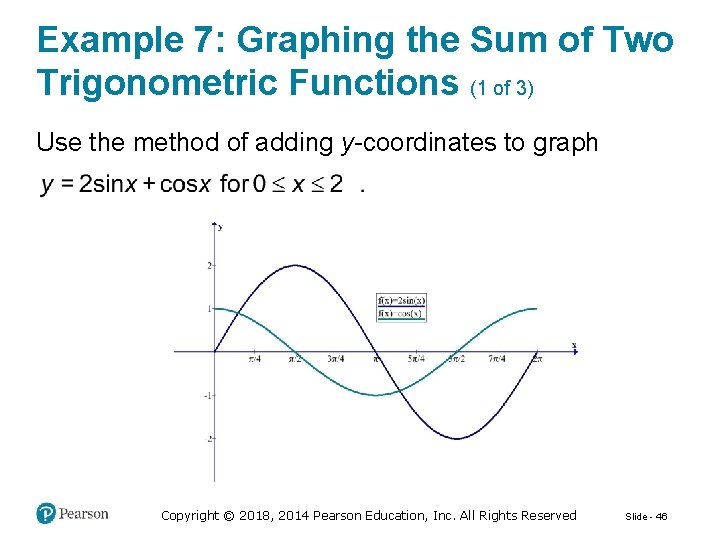
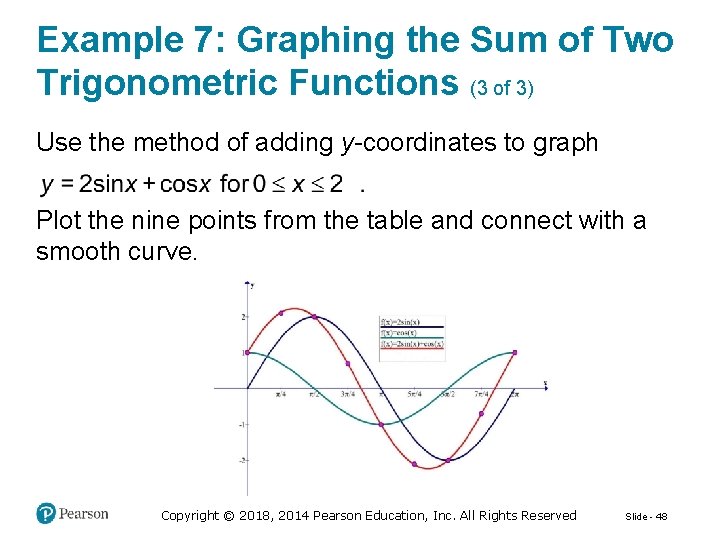
Graphing the Sum of Two Trigonometric Functions We can graph the sum of two (or more) trigonometric functions using a method that involves adding y-coordinates. For example, to graph y = sin x + cos x, we begin by graphing in the same rectangular coordinate system. Then we select several values of x at which we add the y-coordinates of sin x and cos x. Plotting the points (x, sin x + cos x) and joining them with a smooth curve gives the graph of the desired function. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 45

Example 7: Graphing the Sum of Two Trigonometric Functions (1 of 3) Use the method of adding y-coordinates to graph Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 46

Example 7: Graphing the Sum of Two Trigonometric Functions (2 of 3) Use the method of adding y-coordinates to graph Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 47

Example 7: Graphing the Sum of Two Trigonometric Functions (3 of 3) Use the method of adding y-coordinates to graph Plot the nine points from the table and connect with a smooth curve. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 48

Example 8: Modeling Periodic Behavior (1 of 5) A region that is 30° north of the Equator averages a minimum of 10 hours of daylight in December. Hours of daylight are at a maximum of 14 hours in June. Let x represent the month of the year, with 1 for January, 2 for February, 3 for March, and 12 for December. If y represents the number of hours of daylight in month x, use a sine to model the hours function of the form of daylight. Because the hours of daylight range from a minimum of 10 to a maximum of 14, the curve oscillates about the middle value, 12 hours. Thus, D = 12. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 49

Example 8: Modeling Periodic Behavior (2 of 5) A region that is 30° north of the Equator averages a minimum of 10 hours of daylight in December. Hours of daylight are at a maximum of 14 hours in June. Let x represent the month of the year, with 1 for January, 2 for February, 3 for March, and 12 for December. If y represents the number of hours of daylight in month x, use a sine to model the hours function of the form of daylight. The maximum number of hours of daylight is 14, which is 2 hours more than 12 hours. Thus, A, the amplitude, is 2; A = 2. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 50

Example 8: Modeling Periodic Behavior (3 of 5) A region that is 30° north of the Equator averages a minimum of 10 hours of daylight in December. Hours of daylight are at a maximum of 14 hours in June. Let x represent the month of the year, with 1 for January, 2 for February, 3 for March, and 12 for December. If y represents the number of hours of daylight in month x, use a sine to model the hours function of the form of daylight. One complete cycle occurs over a period of 12 months. Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 51

Example 8: Modeling Periodic Behavior (4 of 5) The starting point of the cycle is March, x = 3. The phase shift is Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 52

Example 8: Modeling Periodic Behavior (5 of 5) A region that is 30° north of the Equator averages a minimum of 10 hours of daylight in December. Hours of daylight are at a maximum of 14 hours in June. Let x represent the month of the year, with 1 for January, 2 for February, 3 for March, and 12 for December. If y represents the number of hours of daylight in month x, use a sine function of the form to model the hours of daylight. The equation that models the hours of daylight is Copyright © 2018, 2014 Pearson Education, Inc. All Rights Reserved Slide - 53
 Sin graph points
Sin graph points Sine function transformations
Sine function transformations 9-5 practice graphing trigonometric functions
9-5 practice graphing trigonometric functions 4-4 graphing sine and cosine functions worksheet answers
4-4 graphing sine and cosine functions worksheet answers Sine rule graph
Sine rule graph Horizontal phase shift
Horizontal phase shift Trig function transformations
Trig function transformations Graph of sine and cosine functions
Graph of sine and cosine functions Reflection of sine graph
Reflection of sine graph Sinusoidal graphs
Sinusoidal graphs Transformations of sine and cosine functions
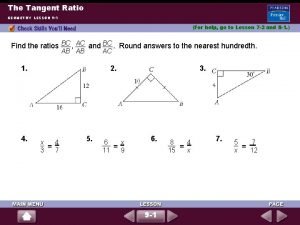
Transformations of sine and cosine functions Practice 9-1 the tangent ratio
Practice 9-1 the tangent ratio Cosine rule to find side
Cosine rule to find side Sine and cosine law maze
Sine and cosine law maze Sohcahtoa rule
Sohcahtoa rule Sine and cosine rule
Sine and cosine rule Inverse of sin
Inverse of sin When to use sine and cosine rule
When to use sine and cosine rule Sine and cosine word problems
Sine and cosine word problems 8-3 practice trigonometry
8-3 practice trigonometry Burj khalifa trigonometry
Burj khalifa trigonometry Fourier series half range
Fourier series half range How to find amplitude of sine function
How to find amplitude of sine function Trig graph
Trig graph Dr frost sine rule
Dr frost sine rule The sine and cosine curves intersect infinitely
The sine and cosine curves intersect infinitely Year 9 trigonometry
Year 9 trigonometry Lesson 8-4 sine and cosine ratios answers
Lesson 8-4 sine and cosine ratios answers Ratio for tangent
Ratio for tangent Fourier series half range
Fourier series half range Degree and leading coefficient
Degree and leading coefficient Trig magic triangles
Trig magic triangles Sine cosine tangent circle
Sine cosine tangent circle Cosine quadrants
Cosine quadrants Hypotenuse adjacent opposite
Hypotenuse adjacent opposite Injuria sine damno and damnum sine injuria difference
Injuria sine damno and damnum sine injuria difference Nullum crimen nulla poena sine lege
Nullum crimen nulla poena sine lege Nullum crimen sine lege nulla poena sine lege
Nullum crimen sine lege nulla poena sine lege State bugs in software testing
State bugs in software testing Graphs that enlighten and graphs that deceive
Graphs that enlighten and graphs that deceive Speed and velocity
Speed and velocity Horizontal asymptote rules
Horizontal asymptote rules Quadratic functions and their graphs
Quadratic functions and their graphs Lesson 1-2 analyzing graphs of functions and relations
Lesson 1-2 analyzing graphs of functions and relations Removable and nonremovable discontinuity
Removable and nonremovable discontinuity Algebra graphs and functions
Algebra graphs and functions 2-5 graphs of expense and revenue functions
2-5 graphs of expense and revenue functions 1-2 analyzing graphs of functions and relations
1-2 analyzing graphs of functions and relations Chapter 1 functions and their graphs
Chapter 1 functions and their graphs Analyzing graphs of functions and relations
Analyzing graphs of functions and relations 2-7 absolute value functions and graphs
2-7 absolute value functions and graphs Rational functions and their graphs
Rational functions and their graphs Common functions and their graphs
Common functions and their graphs Rational function characteristics
Rational function characteristics