GRAPHING SINE AND COSINE FUNCTIONS In previous chapters

GRAPHING SINE AND COSINE FUNCTIONS In previous chapters you learned that the graph of y = a • f (x – h) + k is related to the graph of y = | a | • f (x) by horizontal and vertical translations and by a reflection when a is negative. This also applies to sine, cosine, and tangent functions.

GRAPHING SINE AND COSINE FUNCTIONS TRANSFORMATIONS OF SINE AND COSINE GRAPHS To obtain the graph of y = a sin b (x – h) + k or y = a cos b (x – h) + k Transform the graph of y = | a | sin bx or y = | a | cos bx as follows.

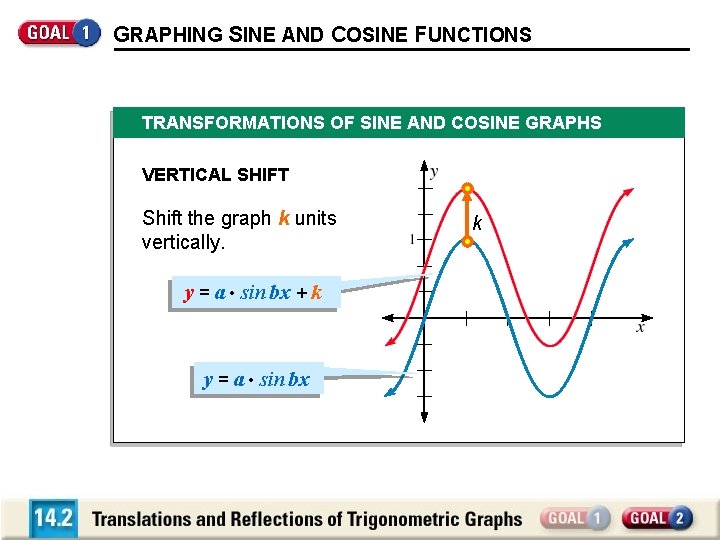
GRAPHING SINE AND COSINE FUNCTIONS TRANSFORMATIONS OF SINE AND COSINE GRAPHS VERTICAL SHIFT Shift the graph k units vertically. y = a • sin bx + k y = a • sin bx k

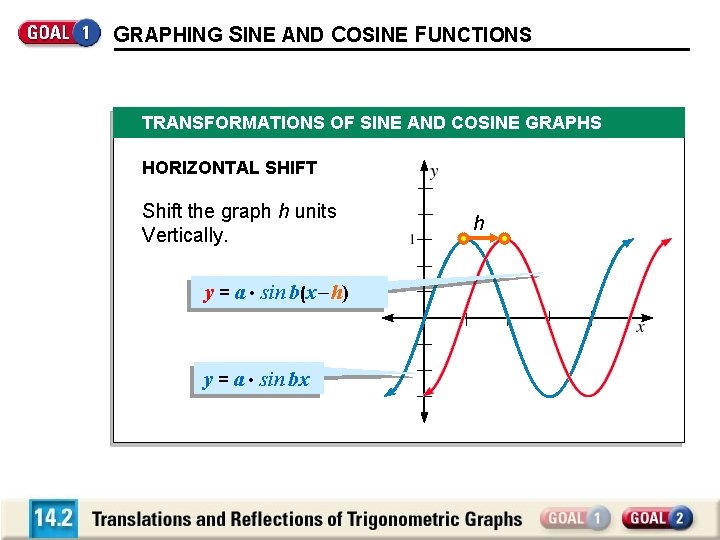
GRAPHING SINE AND COSINE FUNCTIONS TRANSFORMATIONS OF SINE AND COSINE GRAPHS HORIZONTAL SHIFT Shift the graph h units Vertically. y = a • sin b(x – h) y = a • sin bx h

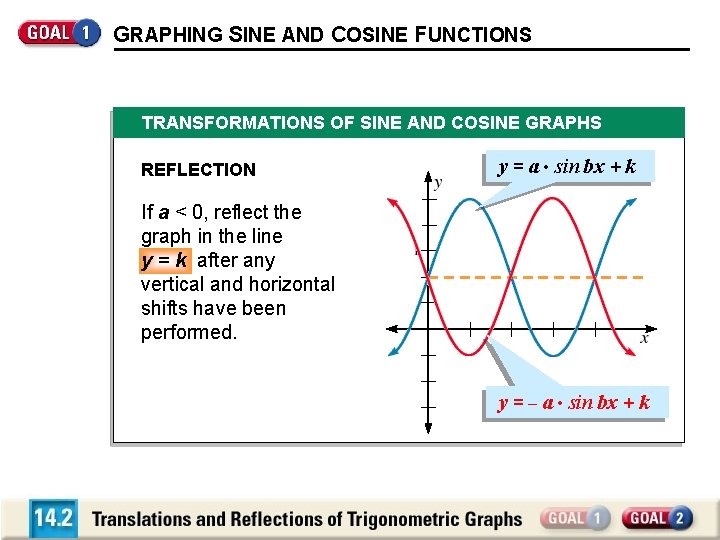
GRAPHING SINE AND COSINE FUNCTIONS TRANSFORMATIONS OF SINE AND COSINE GRAPHS REFLECTION y = a • sin bx + k If a < 0, reflect the graph in the line y = k after any vertical and horizontal shifts have been performed. y = – a • sin bx + k

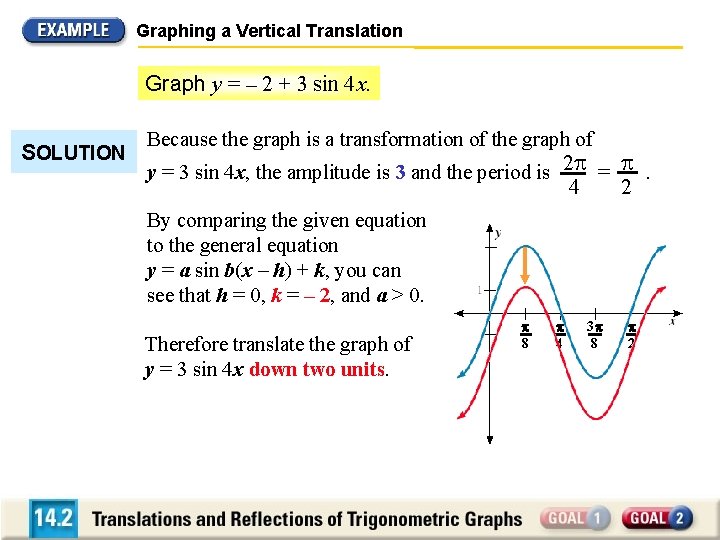
Graphing a Vertical Translation Graph y = – 2 + 3 sin 4 x. SOLUTION Because the graph is a transformation of the graph of y = 3 sin 4 x, the amplitude is 3 and the period is 2 = . 2 4 By comparing the given equation to the general equation y = a sin b(x – h) + k, you can see that h = 0, k = – 2, and a > 0. Therefore translate the graph of y = 3 sin 4 x down two units. 8 4 3 8 2

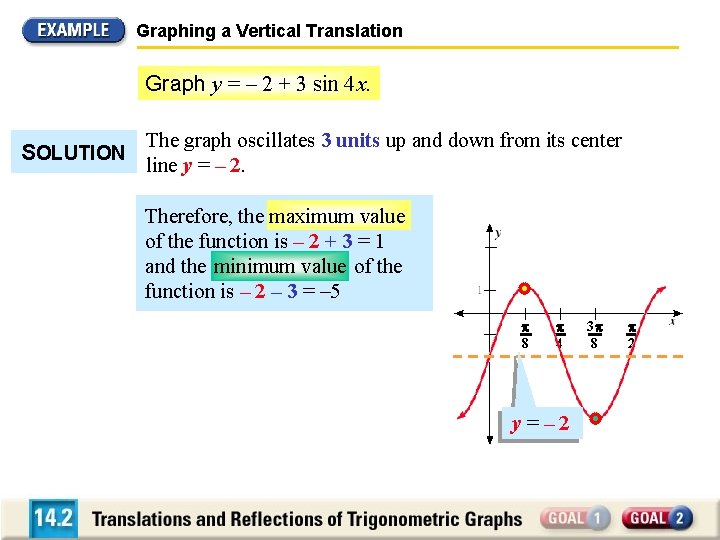
Graphing a Vertical Translation Graph y = – 2 + 3 sin 4 x. SOLUTION The graph oscillates 3 units up and down from its center line y = – 2. Therefore, the maximum value of the function is – 2 + 3 = 1 and the minimum value of the function is – 2 – 3 = – 5 8 4 y=– 2 3 8 2

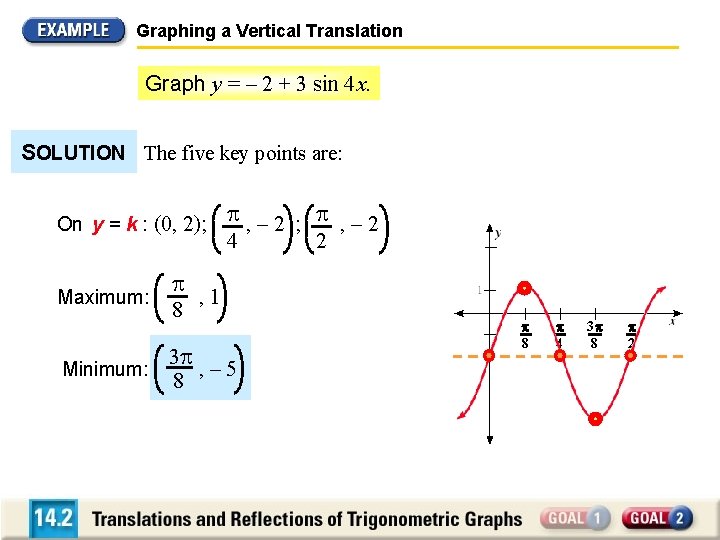
Graphing a Vertical Translation Graph y = – 2 + 3 sin 4 x. SOLUTION The five key points are: On y = k : (0, 2); Maximum: Minimum: , – 2 ; , – 2 4 2 , 1 8 3 , – 5 8 8 4 3 8 2

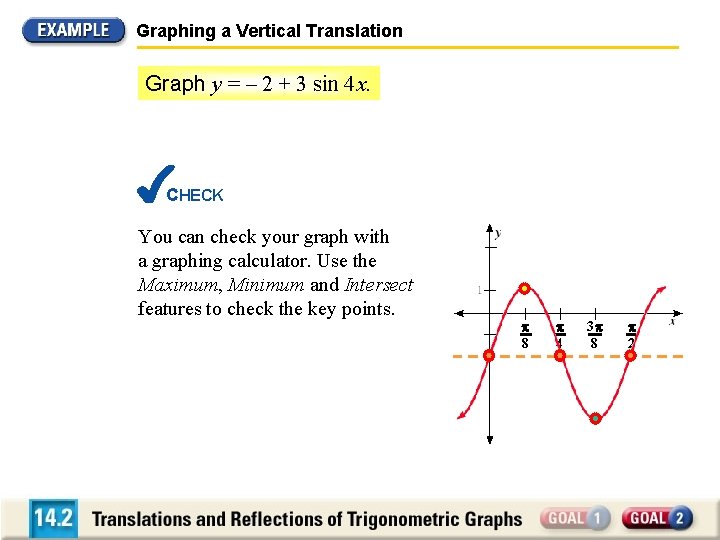
Graphing a Vertical Translation Graph y = – 2 + 3 sin 4 x. CHECK You can check your graph with a graphing calculator. Use the Maximum, Minimum and Intersect features to check the key points. 8 4 3 8 2

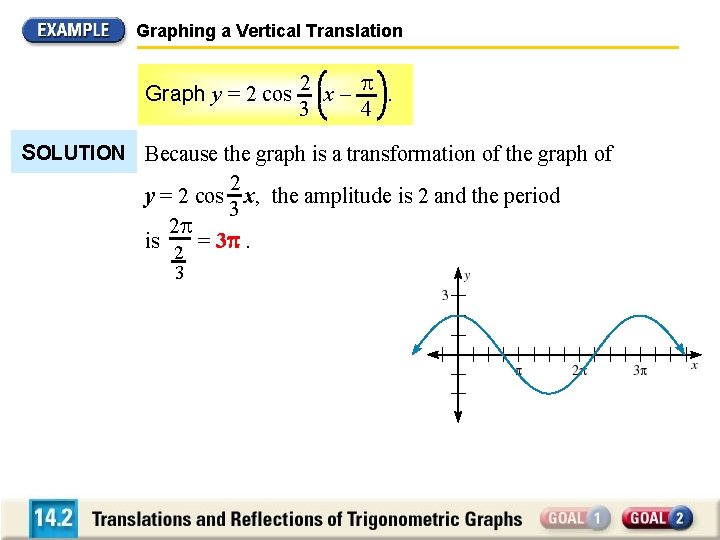
Graphing a Vertical Translation Graph y = 2 cos 2 x – . 3 4 SOLUTION Because the graph is a transformation of the graph of 2 y = 2 cos x, the amplitude is 2 and the period 3 2 is = 3 . 2 3

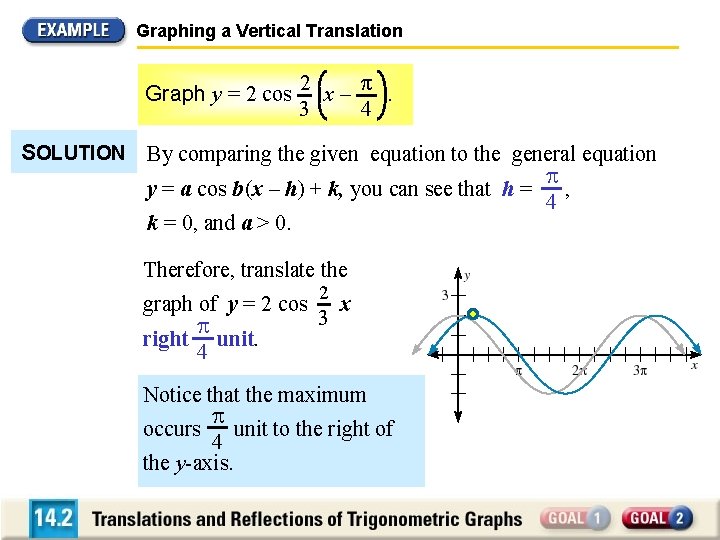
Graphing a Vertical Translation Graph y = 2 cos 2 x – π. 3 4 SOLUTION By comparing the given equation to the general equation y = a cos b (x – h) + k, you can see that h = , 4 k = 0, and a > 0. Therefore, translate the 2 graph of y = 2 cos x 3 right unit. 4 Notice that the maximum occurs unit to the right of 4 the y-axis.

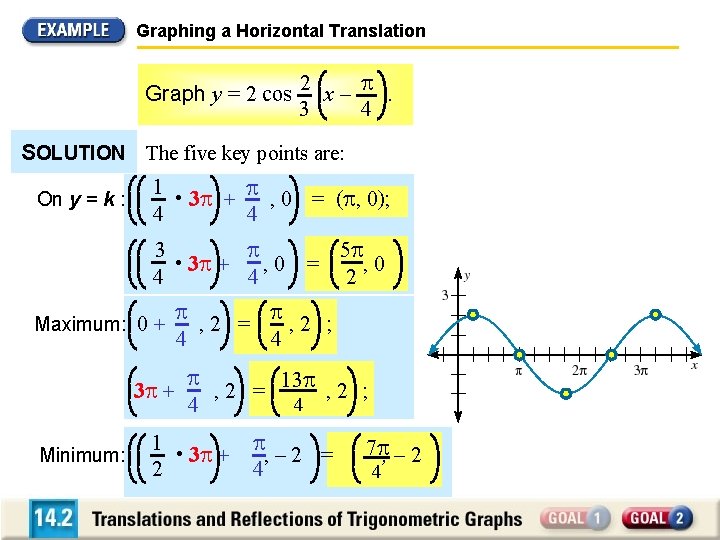
Graphing a Horizontal Translation Graph y = 2 cos 2 x – . 3 4 SOLUTION The five key points are: On y = k : 1 • 3 + , 0 = ( , 0); 4 4 3 • 3 + , 0 4 4 Maximum: 0 + 5 , 0 2 , 2 = , 2 ; 4 4 3 + Minimum: = , 2 = 13 , 2 ; 4 4 1 • 3 + 2 , – 2 = 4 7 , – 2 4

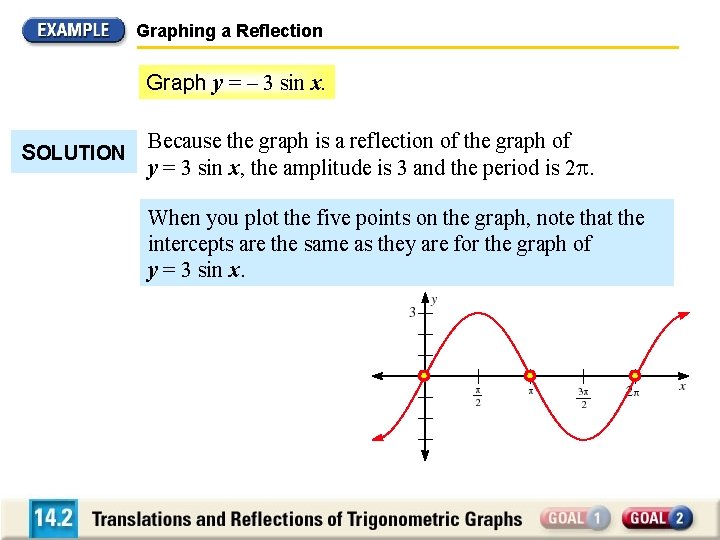
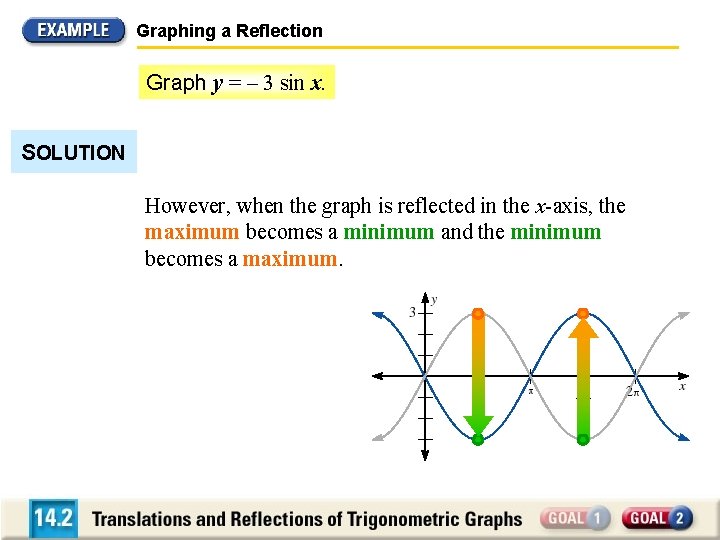
Graphing a Reflection Graph y = – 3 sin x. SOLUTION Because the graph is a reflection of the graph of y = 3 sin x, the amplitude is 3 and the period is 2. When you plot the five points on the graph, note that the intercepts are the same as they are for the graph of y = 3 sin x.

Graphing a Reflection Graph y = – 3 sin x. SOLUTION However, when the graph is reflected in the x-axis, the maximum becomes a minimum and the minimum becomes a maximum.

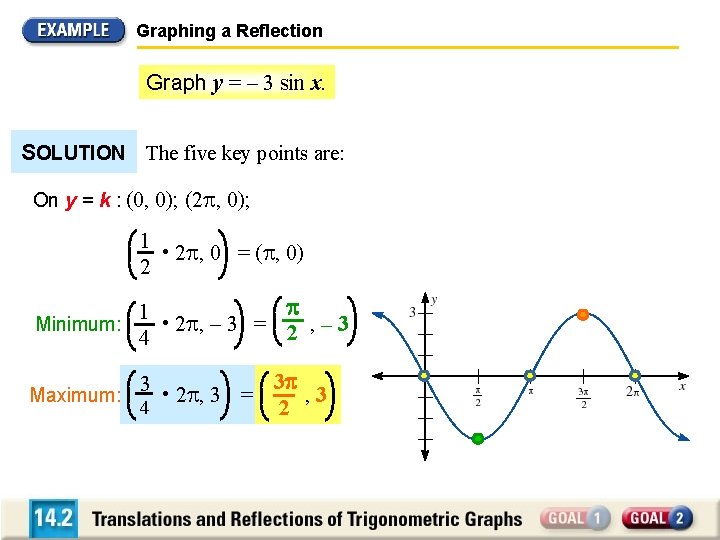
Graphing a Reflection Graph y = – 3 sin x. SOLUTION The five key points are: On y = k : (0, 0); (2 , 0); 1 • 2 , 0 = ( , 0) 2 1 Minimum: • 2 , – 3 = 2 , – 3 4 Maximum: 3 • 2 , 3 = 3 , 3 4 2

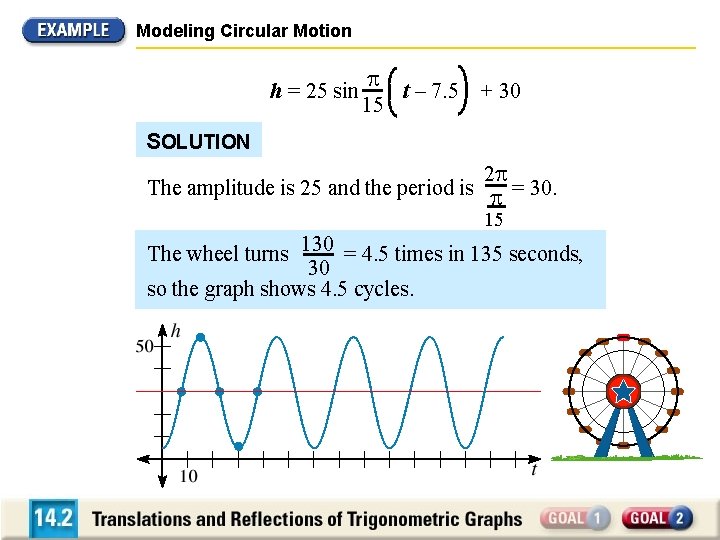
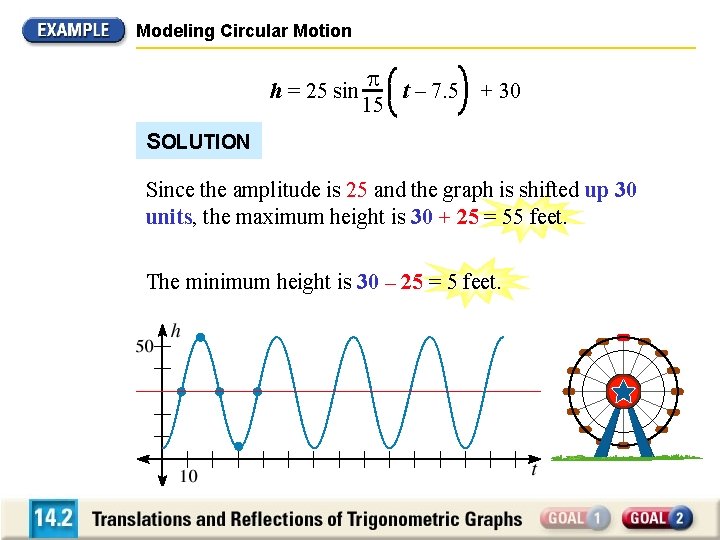
Modeling Circular Motion FERRIS WHEEL You are riding a Ferris wheel. Your height h (in feet) above the ground at any time t (in seconds) can be modeled by the following equation: h = 25 sin t – 7. 5 + 30 15 The Ferris wheel turns for 135 seconds before it stops to let the first passengers off. Graph your height above the ground as a function of time. What are your minimum and maximum heights above the ground?

Modeling Circular Motion h = 25 sin t – 7. 5 + 30 15 SOLUTION 2 The amplitude is 25 and the period is = 30. 15 The wheel turns 130 = 4. 5 times in 135 seconds, 30 so the graph shows 4. 5 cycles.

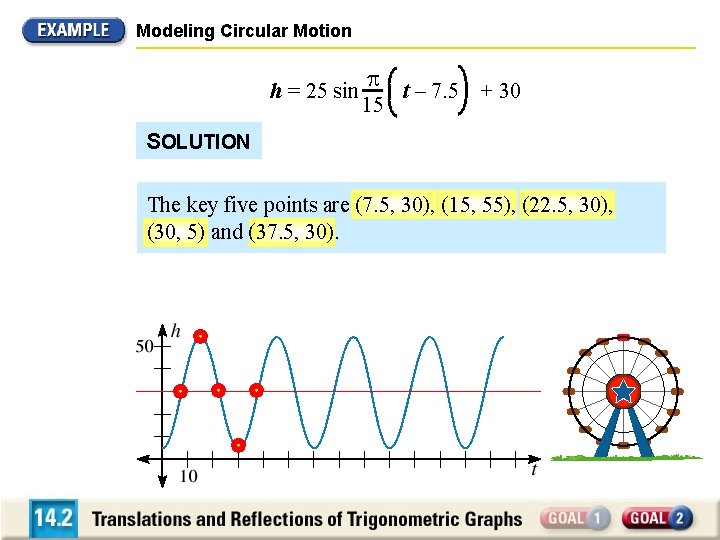
Modeling Circular Motion h = 25 sin t – 7. 5 + 30 15 SOLUTION The key five points are (7. 5, 30), (15, 55), (22. 5, 30), (30, 5) and (37. 5, 30).

Modeling Circular Motion h = 25 sin t – 7. 5 + 30 15 SOLUTION Since the amplitude is 25 and the graph is shifted up 30 units, the maximum height is 30 + 25 = 55 feet. The minimum height is 30 – 25 = 5 feet.

GRAPHING TANGENT FUNCTIONS TRANSFORMATIONS OF TANGENT GRAPHS To obtain the graph of y = a tan b (x – h) + k transform the graph of y = | a | tan bx as follows. • Shift the graph k units vertically and h units horizontally. • Then, if a < 0, reflect the graph in the line y = k.

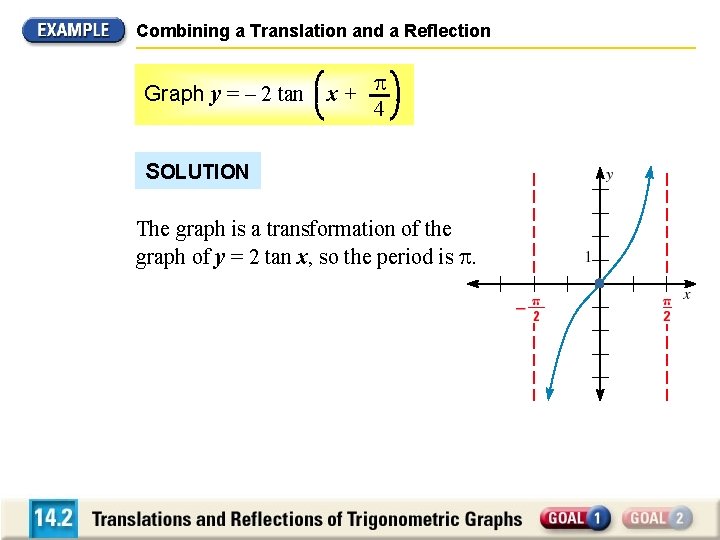
Combining a Translation and a Reflection Graph y = – 2 tan x+ . 4 SOLUTION The graph is a transformation of the graph of y = 2 tan x, so the period is .

Combining a Translation and a Reflection Graph y = – 2 tan x+ . 4 SOLUTION By comparing the given equation to y = a tan b (x – h) + k, you can see that h = – , k = 0, and a < 0. 4 Therefore translate the graph of y = 2 tan x left unit and then 4 reflect it in the x-axis.

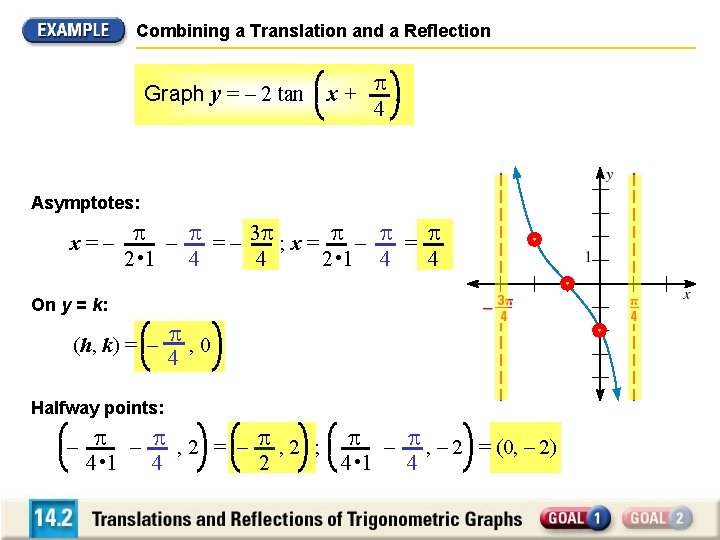
Combining a Translation and a Reflection Graph y = – 2 tan x+ . 4 Asymptotes: x = – – = – 3 ; x = – = 2 • 1 4 4 On y = k: (h, k) = – , 0 4 Halfway points: – – , 2 = – , 2 ; – , – 2 = (0, – 2) 4 • 1 4 2 4 • 1 4