1 5 Graphs of Sine and Cosine Functions

1. 5 Graphs of Sine and Cosine Functions Part 4

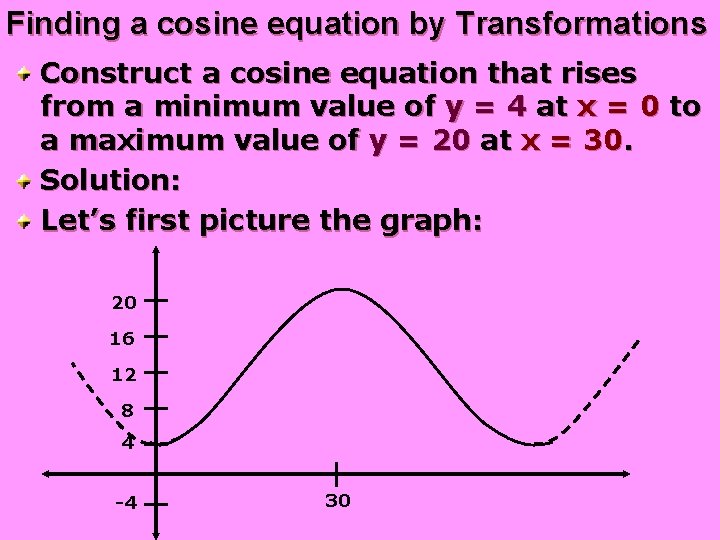
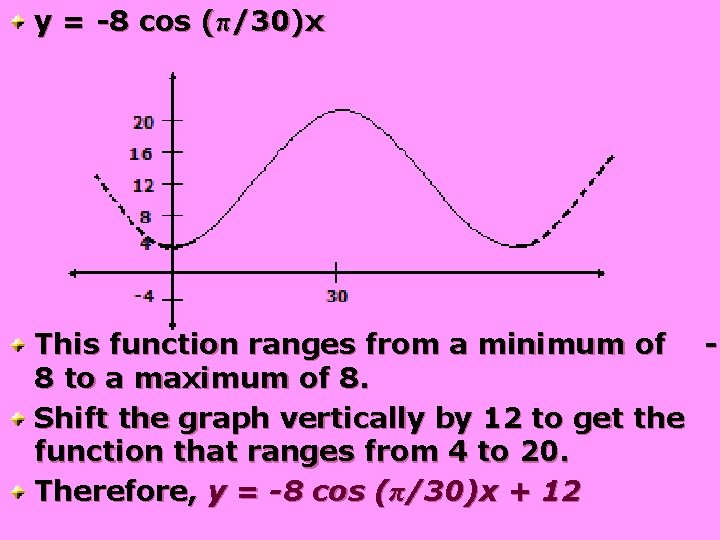
Finding a cosine equation by Transformations Construct a cosine equation that rises from a minimum value of y = 4 at x = 0 to a maximum value of y = 20 at x = 30. Solution: Let’s first picture the graph: 20 16 12 8 4 -4 30

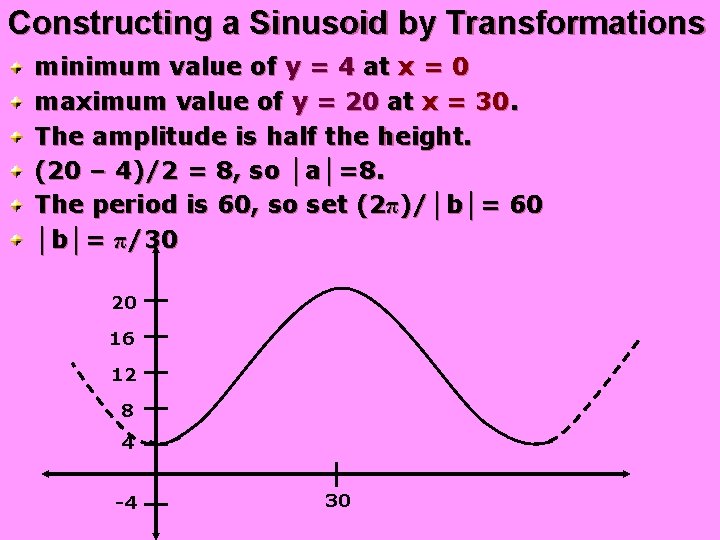
Constructing a Sinusoid by Transformations minimum value of y = 4 at x = 0 maximum value of y = 20 at x = 30. The amplitude is half the height. (20 – 4)/2 = 8, so │a│=8. The period is 60, so set (2π)/│b│= 60 │b│= π/30 20 16 12 8 4 -4 30

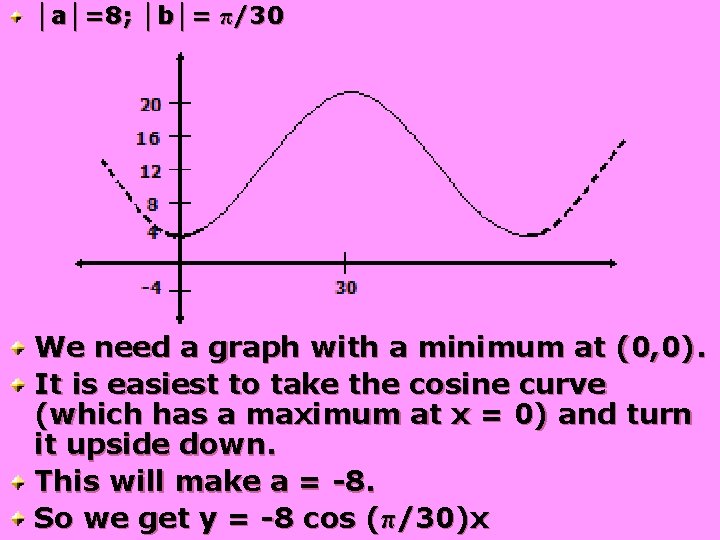
│a│=8; │b│= π/30 We need a graph with a minimum at (0, 0). It is easiest to take the cosine curve (which has a maximum at x = 0) and turn it upside down. This will make a = -8. So we get y = -8 cos (π/30)x

y = -8 cos (π/30)x This function ranges from a minimum of 8 to a maximum of 8. Shift the graph vertically by 12 to get the function that ranges from 4 to 20. Therefore, y = -8 cos (π/30)x + 12

Sine and cosine functions can be used to model many real-life situations We will do an example using the cyclic motion of a ferris wheel.

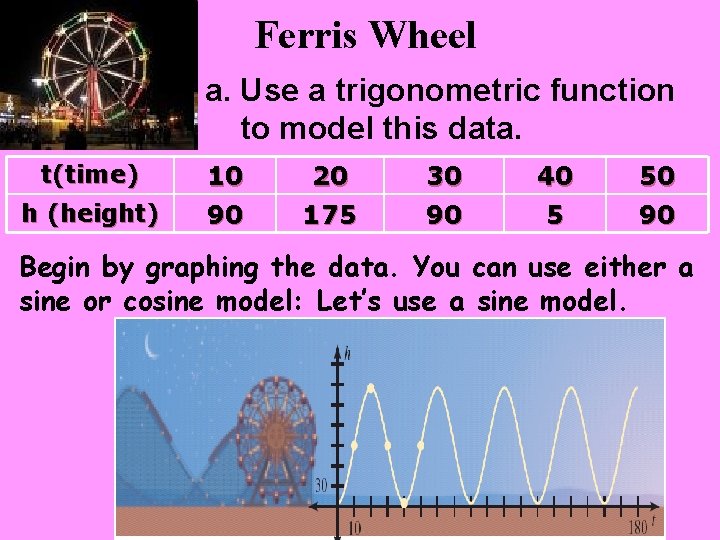
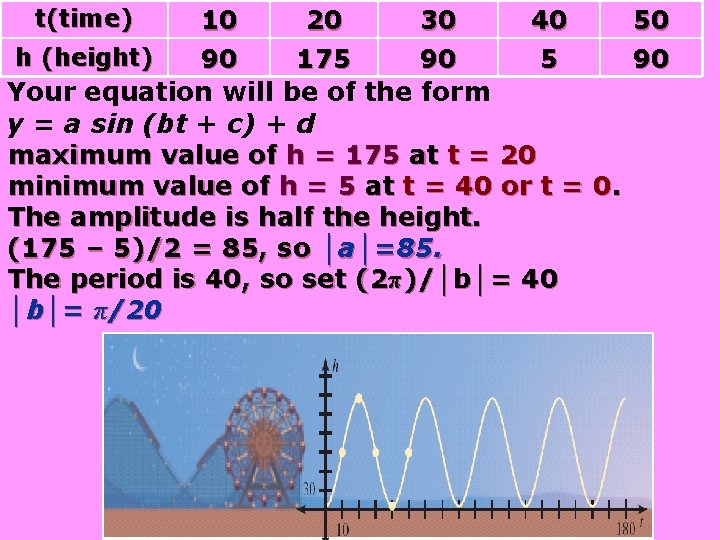
Ferris Wheel Suppose you are riding a Ferris wheel. As it turns, your height h (in ft) varies with the time t (in sec): The table shows your height during various times: t(time) 10 20 30 40 50 h (height) 90 175 90 a. Use a trigonometric function to model this data. b. Find the height at 35 sec and 60 sec.

Ferris Wheel EXAMPLE 3 a. Use a trigonometric function to model this data. t(time) h (height) 10 90 20 175 30 90 40 5 50 90 Begin by graphing the data. You can use either a sine or cosine model: Let’s use a sine model.

10 20 30 40 50 h (height) 90 175 90 Your equation will be of the form y = a sin (bt + c) + d maximum value of h = 175 at t = 20 minimum value of h = 5 at t = 40 or t = 0. The amplitude is half the height. (175 – 5)/2 = 85, so │a│=85. The period is 40, so set (2π)/│b│= 40 │b│= π/20 t(time)

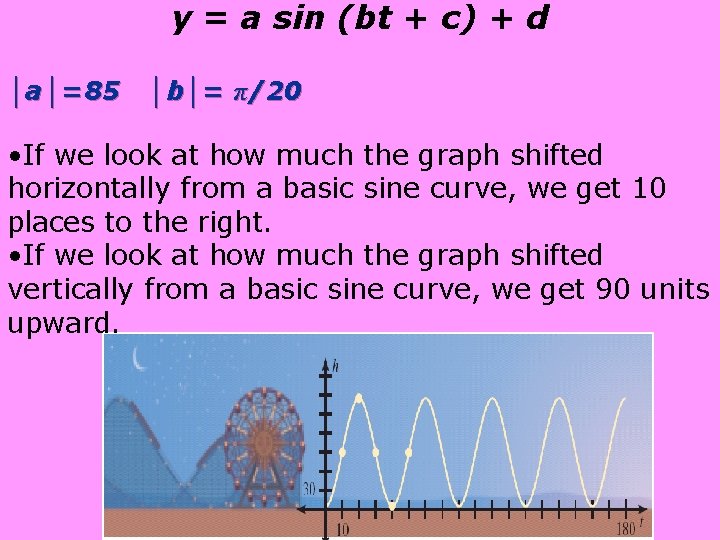
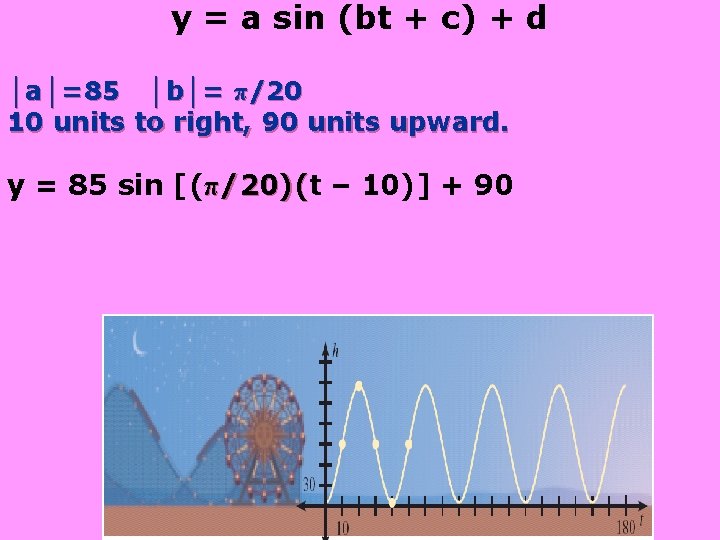
y = a sin (bt + c) + d │a│=85 │b│= π/20 • If we look at how much the graph shifted horizontally from a basic sine curve, we get 10 places to the right. • If we look at how much the graph shifted vertically from a basic sine curve, we get 90 units upward.

y = a sin (bt + c) + d │a│=85 │b│= π/20 10 units to right, 90 units upward. y = 85 sin [(π/20)(t /20)( – 10)] + 90

y = 85 sin [(π/20)(t /20)( – 10)] + 90 b. Find the height at 35 sec and 60 sec. Plug in 35 and 60 for t. Π h = 85 sin (20 (35 – 10)) + 90 =29. 896 ft Π h = 85 sin (20(60 – 10)) + 90 = 175 ft

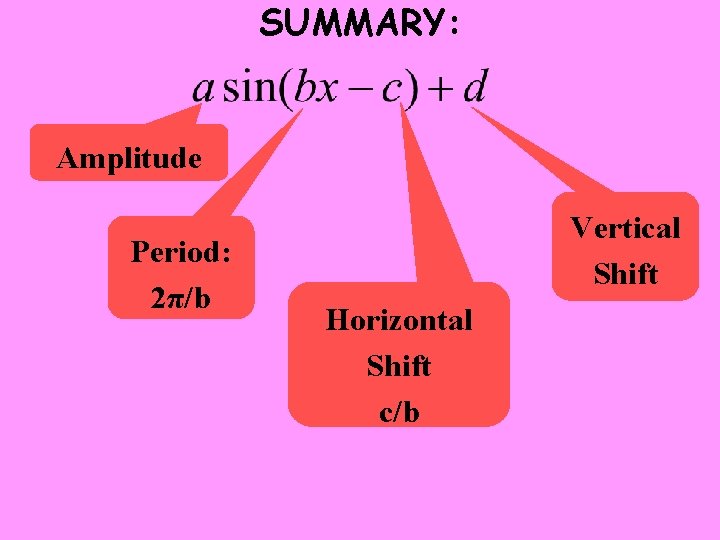
SUMMARY: Amplitude Period: 2π/b Vertical Shift Horizontal Shift c/b

Classwork Section 1. 5 Worksheet – Applications of Trigonometry Models 1. 1 – 1. 5 Test Monday

Homework Pg 168 – 170 69 – 76, 83 – 86, 93