Author Kyle Heffelbower Trigonometric Functions Definitions Trigonometric functions

Author: Kyle Heffelbower Trigonometric Functions

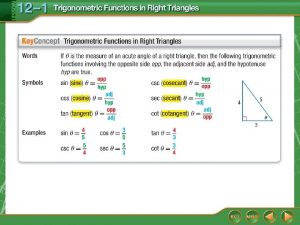
Definitions �Trigonometric functions- sine, cosine, and tangent �Sine is abbreviated sin �Cosine is abbreviated cos �Tangent is abbreviated tan �The Greek letter theta (Θ) is used as a variable for angles. �Hypotenuse is the side opposite the right angle in a right triangle. The longest side of a right triangle.

Review of Trigonometric Ratios �For any RIGHT triangle the trigonometric ratios allow us to find out information about the side lengths and angle measures when given some basic information
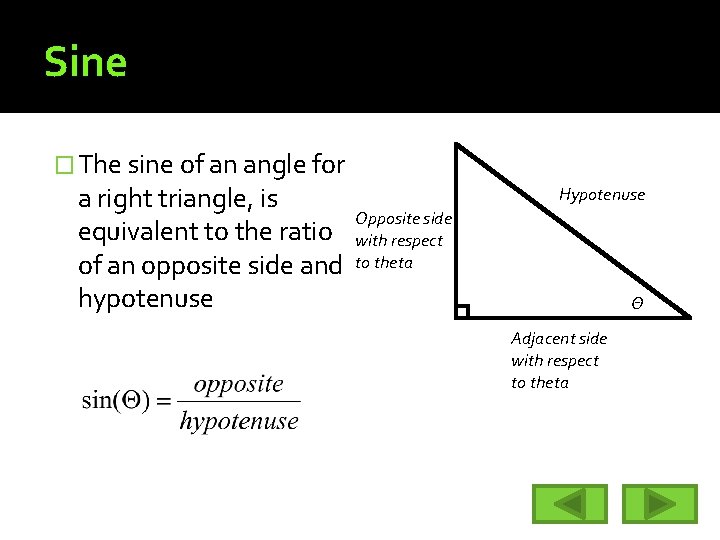
Sine � The sine of an angle for a right triangle, is equivalent to the ratio of an opposite side and hypotenuse Hypotenuse Opposite side with respect to theta Θ Adjacent side with respect to theta

Cosine � The cosine of an angle for a right triangle, is equivalent to the ratio of an adjacent side and hypotenuse Hypotenuse Opposite side with respect to theta Θ Adjacent side with respect to theta
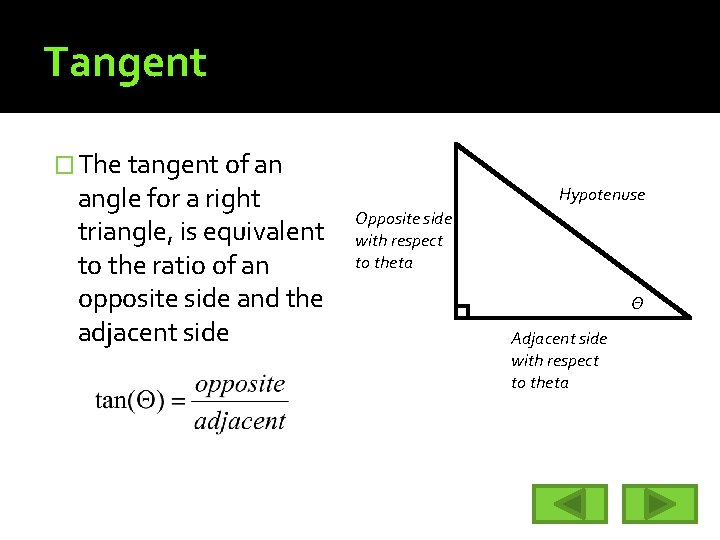
Tangent � The tangent of an angle for a right triangle, is equivalent to the ratio of an opposite side and the adjacent side Hypotenuse Opposite side with respect to theta Θ Adjacent side with respect to theta

Trigonometric Ratios �All of these relationships can easily be remembered with the acronym S O H C A H i n e p p o s i t e y p o t e n u s e o s i n e d j a c e n t y p o t e n u s e T a n g e n t O A p d p j o a s c i e t n e t
Alright… �Now that we have done a bit of review, let’s get some practice in before we get to the new stuff.

Practice!! �Choose the best answer for the length of the h given the right triangle below. 13 meters a. 9. 959 meters correct b. 8. 356 meters cos c. -3. 411 meters rad d. 16. 970 meters divide 50° h

Right Plan But Watch Out!! �While your idea is flawless and you did correctly solve this, you did it for radians and not degrees. �There are two popular ways to measure angles- degrees is one, radians is the other �Whenever you are working with trigonometric functions- sine, cosine, tangent - you need to make sure your calculator is in the right MODE Help with switching you calculator Try again

Calculator Help �For the TI-81 through TI-84 the radian/degree shift is in the “mode” menu. The button is next to the 2 nd key. �For the TI-n. Spire the radian/degree shift is in the general settings menu �Many scientific calculators have a units shift button. On the screen it will say either “deg” or “rad” in little letters.

Arithmetic Issue �Nice job recognizing that it is a right triangle and you need to use sine to complete it, but it is the opposite side divided by the hypotenuse- not the other way around. Let’s take another look

Not Quite �Let’s take another look at the trigonometric ratios and try this out again. �Make sure you are identifying the sides accurately. Let’s try this again!
Amazing!!! �Way to go champion!! �Keep up the good work.

Practice!! �Choose the best answer for the length of the h given the right triangle below. 38° a. 10. 152 meters divide b. 6. 304 meters correct c. 4. 925 meters sin d. 7. 641 meters rad 8 meters x

Right Plan But Watch Out!! �While your idea is flawless and you did correctly solve this, you did it for radians and not degrees. �There are two popular ways to measure angles- degrees is one, radians is the other �Whenever you are working with trigonometric functions- sine, cosine, tangent - you need to make sure your calculator is in the right MODE Help with switching you calculator Try again

Calculator Help �For the TI-81 through TI-84 the radian/degree shift is in the “mode” menu. The button is next to the 2 nd key. �For the TI-n. Spire the radian/degree shift is in the general settings menu �Many scientific calculators have a units shift button. On the screen it will say either “deg” or “rad” in little letters.

Arithmetic Issue �Nice job recognizing that it is a right triangle and you need to use cosine to complete it, but it is the adjacent side divided by the hypotenuse- not the other way around. Let’s take another look

Not Quite �Let’s take another look at the trigonometric ratios and try this out again. �Make sure you are identifying the sides accurately. Let’s try this again!

Amazing!!! �Way to go champion!! �Keep up the good work.
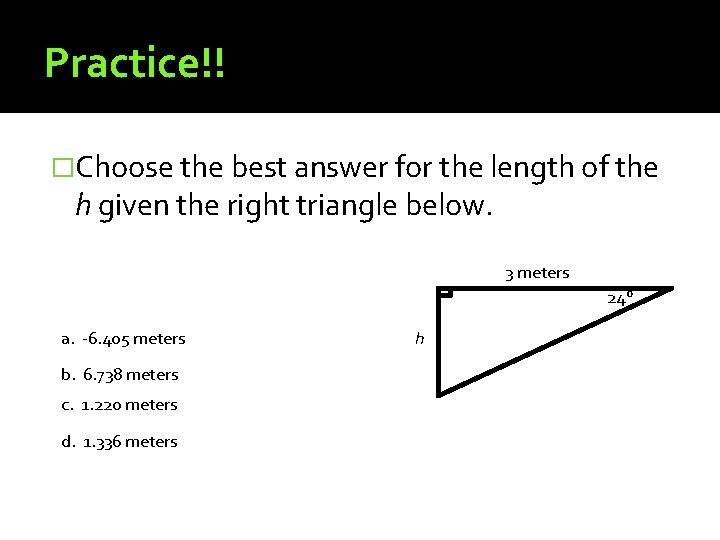
Practice!! �Choose the best answer for the length of the h given the right triangle below. 3 meters 24° a. -6. 405 meters b. 6. 738 meters c. 1. 220 meters d. 1. 336 meters h

Right Plan But Watch Out!! �While your idea is flawless and you did correctly solve this, you did it for radians and not degrees. �There are two popular ways to measure angles- degrees is one, radians is the other �Whenever you are working with trigonometric functions- sine, cosine, tangent - you need to make sure your calculator is in the right MODE Help with switching you calculator Try again

Calculator Help �For the TI-81 through TI-84 the radian/degree shift is in the “mode” menu. The button is next to the 2 nd key. �For the TI-n. Spire the radian/degree shift is in the general settings menu �Many scientific calculators have a units shift button. On the screen it will say either “deg” or “rad” in little letters.

Arithmetic Issue �Nice job recognizing that it is a right triangle and you need to use tangent to complete it, but it is the opposite side divided by the adjacent- not the other way around. Let’s take another look

Not Quite �Let’s take another look at the trigonometric ratios and try this out again. �Make sure you are identifying the sides accurately. Let’s try this again!
Amazing!!! �Way to go champion!! �Keep up the good work.

Nice Job!! �Now that we are caught up to speed in the review of the solving trigonometric ratios, it is time to get to the graphing.

Megaloop � A ride maker decides to crank up the intensity of the “Megaloop. ” She wants to place half of it underground. Always conscious of safety and evacuation necessities she has called on you to discover the distance from the ground at any point on this loop. See if you can help her out. Job one: Let’s get a picture of the scenario.
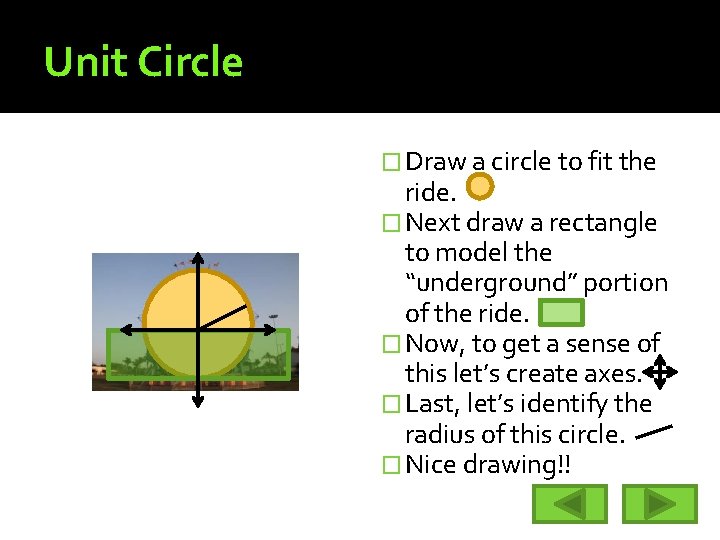
Unit Circle � Draw a circle to fit the ride. � Next draw a rectangle to model the “underground” portion of the ride. � Now, to get a sense of this let’s create axes. � Last, let’s identify the radius of this circle. � Nice drawing!!
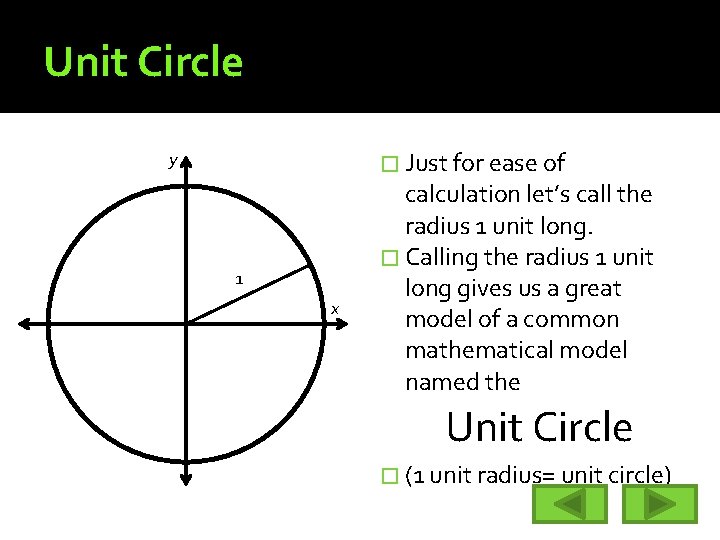
Unit Circle � Just for ease of y 1 x calculation let’s call the radius 1 unit long. � Calling the radius 1 unit long gives us a great model of a common mathematical model named the Unit Circle � (1 unit radius= unit circle)

Let’s Use it!! � As with our evacuation route for the half underground Megaloop, the goal is to find the distance from the ground. In the picture this is the vertical distance from the x-axis. y 1 y x
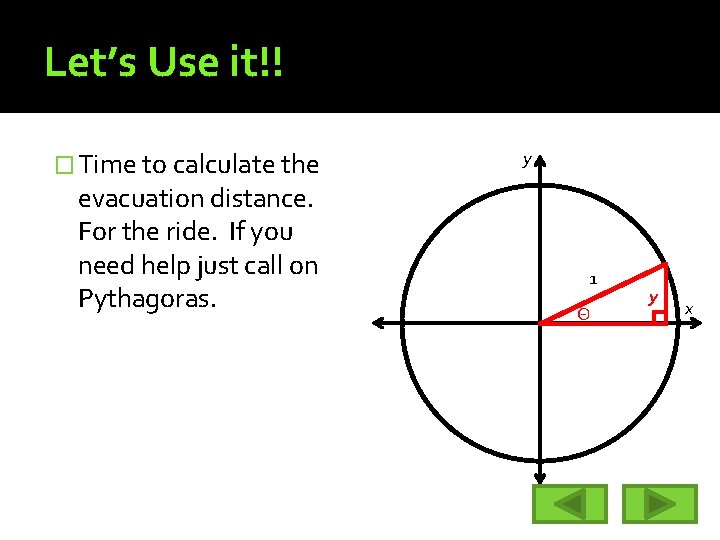
Let’s Use it!! � Time to calculate the evacuation distance. For the ride. If you need help just call on Pythagoras. y 1 Θ y x

Evacuation Distance �For the next activity you will need a scientific calculator in degree mode. �We will take a look at several different right triangles developed from various angles and build a table of values. �Let’s get cracking!!
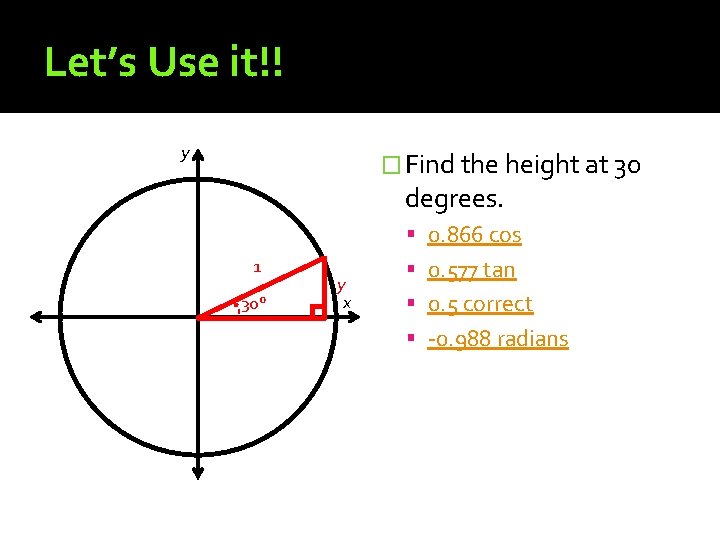
Let’s Use it!! y � Find the height at 30 degrees. 0. 866 cos 1 30° y x 0. 577 tan 0. 5 correct -0. 988 radians

Right On!!! �Great work calculating that distance. �Let’s put that on the table and continue!! Bring on the next one!!

Easy Now… �Remember our Trigonometric ratios and think about what we were given. T S O H C A H i n e p p o s i t e y p o t e n u s e o s i n e d j a c e n t y p o t e n u s e a n g e n t O A p d p j o a s c i e t n e t

Right Plan But Watch Out!! �While your idea is flawless and you did correctly solve this, you did it for radians and not degrees. �There are two popular ways to measure angles- degrees is one, radians is the other �Whenever you are working with trigonometric functions- sine, cosine, tangent - you need to make sure your calculator is in the right MODE Help with switching you calculator Try again

Calculator Help �For the TI-81 through TI-84 the radian/degree shift is in the “mode” menu. The button is next to the 2 nd key. �For the TI-n. Spire the radian/degree shift is in the general settings menu �Many scientific calculators have a units shift button. On the screen it will say either “deg” or “rad” in little letters.

Let’s Use it!! Angle 30 Height 0. 5 45 60 90 y 120 150 180 210 240 270 300 330 � Find the height at 45 1 45° degrees. y x 0. 851 radi 0. 707 correc 1 tan 0. 707 cos 360

Awesome!!! �Nice job putting that together. �Let’s put that on the table and continue!! Bring on the next one!!

Easy Now… �Remember our Trigonometric ratios and think about what we were given. T S O H C A H i n e p p o s i t e y p o t e n u s e o s i n e d j a c e n t y p o t e n u s e a n g e n t O A p d p j o a s c i e t n e t

Right Plan But Watch Out!! �While your idea is flawless and you did correctly solve this, you did it for radians and not degrees. �There are two popular ways to measure angles- degrees is one, radians is the other �Whenever you are working with trigonometric functions- sine, cosine, tangent - you need to make sure your calculator is in the right MODE Help with switching you calculator Try again

Calculator Help �For the TI-81 through TI-84 the radian/degree shift is in the “mode” menu. The button is next to the 2 nd key. �For the TI-n. Spire the radian/degree shift is in the general settings menu �Many scientific calculators have a units shift button. On the screen it will say either “deg” or “rad” in little letters.
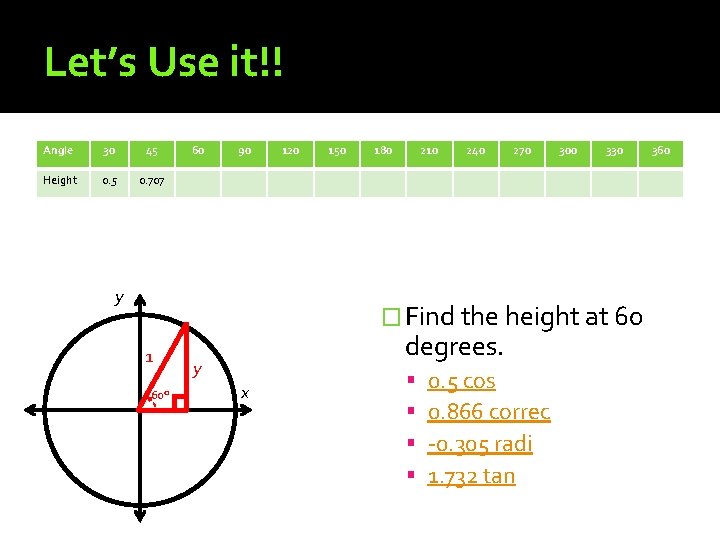
Let’s Use it!! Angle 30 45 Height 0. 5 0. 707 60 90 y 120 150 180 210 240 270 300 330 � Find the height at 60 1 60° degrees. y x 0. 5 cos 0. 866 correc -0. 305 radi 1. 732 tan 360

Perfect!!! �Distance is just right. �Let’s put that on the table and continue!! Bring on the next one!!

Easy Now… �Remember our Trigonometric ratios and think about what we were given. T S O H C A H i n e p p o s i t e y p o t e n u s e o s i n e d j a c e n t y p o t e n u s e a n g e n t O A p d p j o a s c i e t n e t

Right Plan But Watch Out!! �While your idea is flawless and you did correctly solve this, you did it for radians and not degrees. �There are two popular ways to measure angles- degrees is one, radians is the other �Whenever you are working with trigonometric functions- sine, cosine, tangent - you need to make sure your calculator is in the right MODE Help with switching you calculator Try again

Calculator Help �For the TI-81 through TI-84 the radian/degree shift is in the “mode” menu. The button is next to the 2 nd key. �For the TI-n. Spire the radian/degree shift is in the general settings menu �Many scientific calculators have a units shift button. On the screen it will say either “deg” or “rad” in little letters.
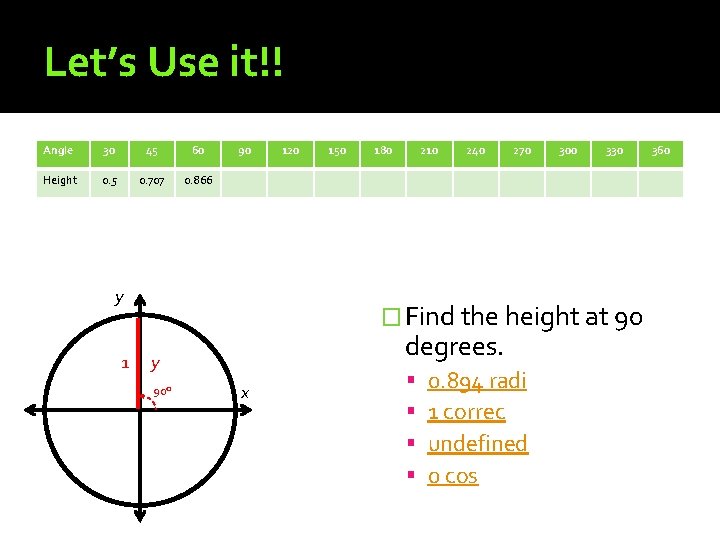
Let’s Use it!! Angle 30 45 60 Height 0. 5 0. 707 0. 866 90 y 1 120 150 180 210 240 270 300 330 � Find the height at 90 degrees. y 90° x 0. 894 radi 1 correc undefined 0 cos 360

Superb!!! �Let’s put that on the table and continue!! Bring on the next one!!

Easy Now… �Remember our Trigonometric ratios and think about what we were given. T S O H C A H i n e p p o s i t e y p o t e n u s e o s i n e d j a c e n t y p o t e n u s e a n g e n t O A p d p j o a s c i e t n e t

Right Plan But Watch Out!! �While your idea is flawless and you did correctly solve this, you did it for radians and not degrees. �There are two popular ways to measure angles- degrees is one, radians is the other �Whenever you are working with trigonometric functions- sine, cosine, tangent - you need to make sure your calculator is in the right MODE Help with switching you calculator Try again

Calculator Help �For the TI-81 through TI-84 the radian/degree shift is in the “mode” menu. The button is next to the 2 nd key. �For the TI-n. Spire the radian/degree shift is in the general settings menu �Many scientific calculators have a units shift button. On the screen it will say either “deg” or “rad” in little letters.

Let’s Use it!! Angle 30 45 60 90 Height 0. 5 0. 707 0. 866 1 y y 120 150 180 210 240 270 300 330 360 � Find the height at 120 degrees. 1 120° x 0. 581 radi -0. 5 cos -1. 732 tan 0. 866 correct

Just Right!!! �Let’s put that on the table and continue!! Bring on the next one!!

Easy Now… �Remember our Trigonometric ratios and think about what we were given. T S O H C A H i n e p p o s i t e y p o t e n u s e o s i n e d j a c e n t y p o t e n u s e a n g e n t O A p d p j o a s c i e t n e t

Right Plan But Watch Out!! �While your idea is flawless and you did correctly solve this, you did it for radians and not degrees. �There are two popular ways to measure angles- degrees is one, radians is the other �Whenever you are working with trigonometric functions- sine, cosine, tangent - you need to make sure your calculator is in the right MODE Help with switching you calculator Try again

Calculator Help �For the TI-81 through TI-84 the radian/degree shift is in the “mode” menu. The button is next to the 2 nd key. �For the TI-n. Spire the radian/degree shift is in the general settings menu �Many scientific calculators have a units shift button. On the screen it will say either “deg” or “rad” in little letters.
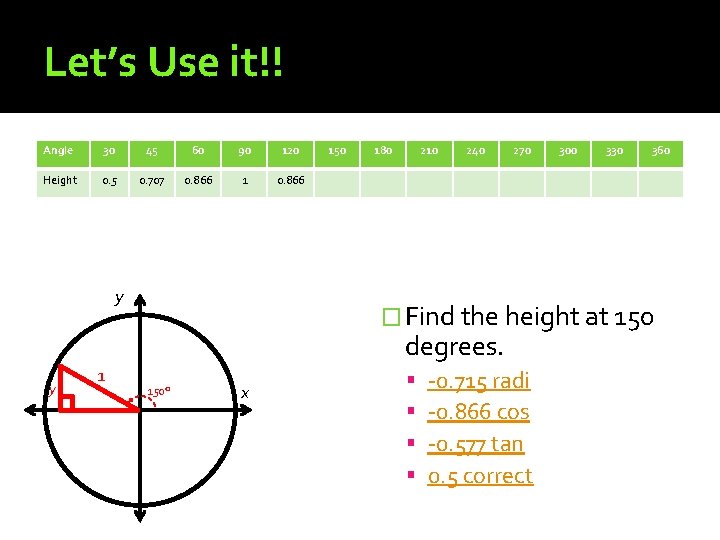
Let’s Use it!! Angle 30 45 60 90 120 Height 0. 5 0. 707 0. 866 1 0. 866 y 150 180 210 240 270 1 330 360 � Find the height at 150 degrees. y 300 150° x -0. 715 radi -0. 866 cos -0. 577 tan 0. 5 correct

Nice Work!!! �Are you beginning to sense a bit of a pattern? �Let’s put that on the table and continue!! Bring on the next one!!

Easy Now… �Remember our Trigonometric ratios and think about what we were given. T S O H C A H i n e p p o s i t e y p o t e n u s e o s i n e d j a c e n t y p o t e n u s e a n g e n t O A p d p j o a s c i e t n e t

Right Plan But Watch Out!! �While your idea is flawless and you did correctly solve this, you did it for radians and not degrees. �There are two popular ways to measure angles- degrees is one, radians is the other �Whenever you are working with trigonometric functions- sine, cosine, tangent - you need to make sure your calculator is in the right MODE Help with switching you calculator Try again

Calculator Help �For the TI-81 through TI-84 the radian/degree shift is in the “mode” menu. The button is next to the 2 nd key. �For the TI-n. Spire the radian/degree shift is in the general settings menu �Many scientific calculators have a units shift button. On the screen it will say either “deg” or “rad” in little letters.
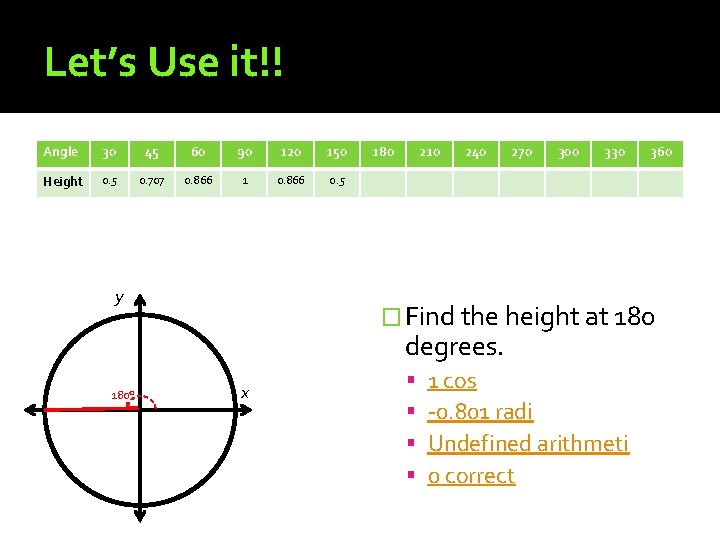
Let’s Use it!! Angle 30 45 60 90 120 150 Height 0. 5 0. 707 0. 866 1 0. 866 0. 5 y 180 210 240 270 300 330 � Find the height at 180 degrees. 180° 360 x 1 cos -0. 801 radi Undefined arithmeti 0 correct
Yea, you got this!!! �Keep on trucking!! �Finish this up. Bring on the next one!!

Easy Now… �Remember our Trigonometric ratios and think about what we were given. T S O H C A H i n e p p o s i t e y p o t e n u s e o s i n e d j a c e n t y p o t e n u s e a n g e n t O A p d p j o a s c i e t n e t

Right Plan But Watch Out!! �While your idea is flawless and you did correctly solve this, you did it for radians and not degrees. �There are two popular ways to measure angles- degrees is one, radians is the other �Whenever you are working with trigonometric functions- sine, cosine, tangent - you need to make sure your calculator is in the right MODE Help with switching you calculator Try again

Calculator Help �For the TI-81 through TI-84 the radian/degree shift is in the “mode” menu. The button is next to the 2 nd key. �For the TI-n. Spire the radian/degree shift is in the general settings menu �Many scientific calculators have a units shift button. On the screen it will say either “deg” or “rad” in little letters.
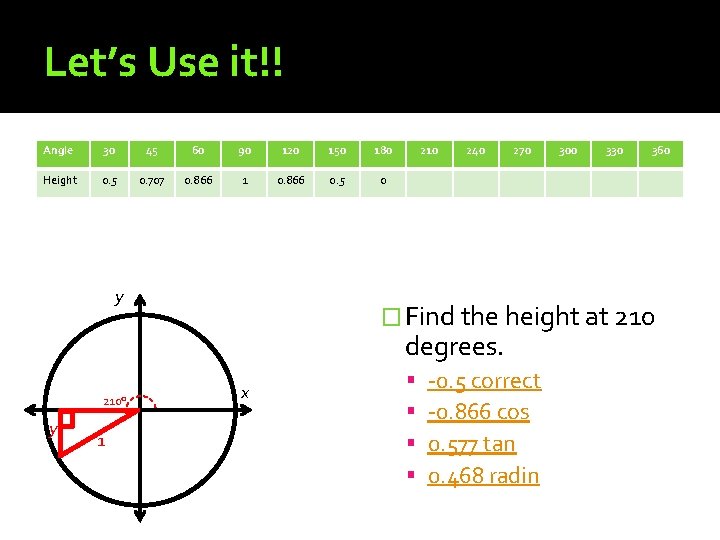
Let’s Use it!! Angle 30 45 60 90 120 150 180 Height 0. 5 0. 707 0. 866 1 0. 866 0. 5 0 y 210 240 270 y 1 330 360 � Find the height at 210 degrees. 210° 300 x -0. 5 correct -0. 866 cos 0. 577 tan 0. 468 radin

Easy Now… �Remember our Trigonometric ratios and think about what we were given. T S O H C A H i n e p p o s i t e y p o t e n u s e o s i n e d j a c e n t y p o t e n u s e a n g e n t O A p d p j o a s c i e t n e t

Right Plan But Watch Out!! �While your idea is flawless and you did correctly solve this, you did it for radians and not degrees. �There are two popular ways to measure angles- degrees is one, radians is the other �Whenever you are working with trigonometric functions- sine, cosine, tangent - you need to make sure your calculator is in the right MODE Help with switching you calculator Try again

Calculator Help �For the TI-81 through TI-84 the radian/degree shift is in the “mode” menu. The button is next to the 2 nd key. �For the TI-n. Spire the radian/degree shift is in the general settings menu �Many scientific calculators have a units shift button. On the screen it will say either “deg” or “rad” in little letters.
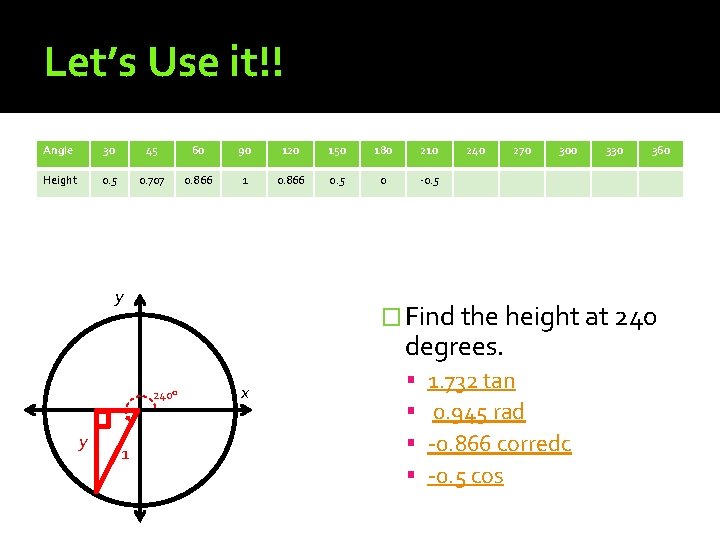
Let’s Use it!! Angle 30 45 60 90 120 150 180 210 Height 0. 5 0. 707 0. 866 1 0. 866 0. 5 0 -0. 5 y 240 270 300 240° 1 360 � Find the height at 240 degrees. y 330 x 1. 732 tan 0. 945 rad -0. 866 corredc -0. 5 cos

Easy Now… �Remember our Trigonometric ratios and think about what we were given. T S O H C A H i n e p p o s i t e y p o t e n u s e o s i n e d j a c e n t y p o t e n u s e a n g e n t O A p d p j o a s c i e t n e t

Right Plan But Watch Out!! �While your idea is flawless and you did correctly solve this, you did it for radians and not degrees. �There are two popular ways to measure angles- degrees is one, radians is the other �Whenever you are working with trigonometric functions- sine, cosine, tangent - you need to make sure your calculator is in the right MODE Help with switching you calculator Try again

Calculator Help �For the TI-81 through TI-84 the radian/degree shift is in the “mode” menu. The button is next to the 2 nd key. �For the TI-n. Spire the radian/degree shift is in the general settings menu �Many scientific calculators have a units shift button. On the screen it will say either “deg” or “rad” in little letters.
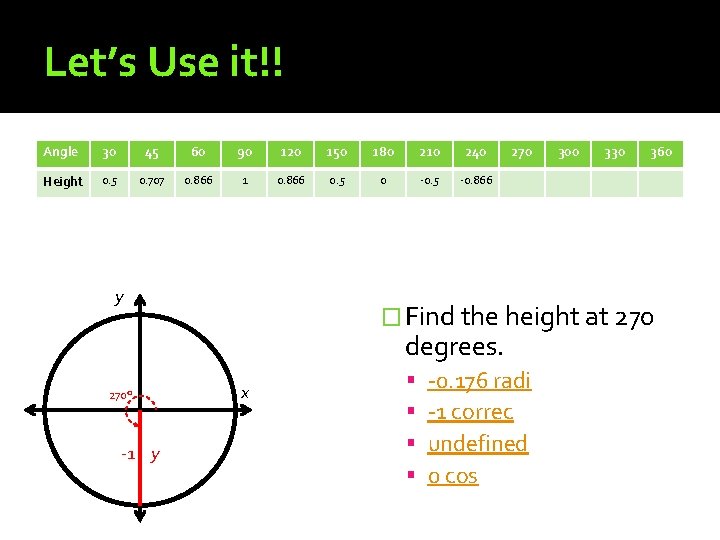
Let’s Use it!! Angle 30 45 60 90 120 150 180 210 240 Height 0. 5 0. 707 0. 866 1 0. 866 0. 5 0 -0. 5 -0. 866 y 270 -1 y 330 360 � Find the height at 270 degrees. 270° 300 x -0. 176 radi -1 correc undefined 0 cos

Easy Now… �Remember our Trigonometric ratios and think about what we were given. T S O H C A H i n e p p o s i t e y p o t e n u s e o s i n e d j a c e n t y p o t e n u s e a n g e n t O A p d p j o a s c i e t n e t

Right Plan But Watch Out!! �While your idea is flawless and you did correctly solve this, you did it for radians and not degrees. �There are two popular ways to measure angles- degrees is one, radians is the other �Whenever you are working with trigonometric functions- sine, cosine, tangent - you need to make sure your calculator is in the right MODE Help with switching you calculator Try again

Calculator Help �For the TI-81 through TI-84 the radian/degree shift is in the “mode” menu. The button is next to the 2 nd key. �For the TI-n. Spire the radian/degree shift is in the general settings menu �Many scientific calculators have a units shift button. On the screen it will say either “deg” or “rad” in little letters.
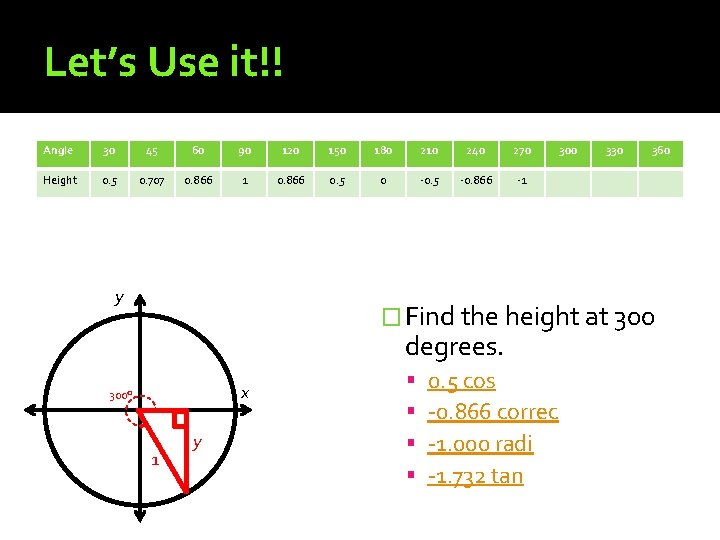
Let’s Use it!! Angle 30 45 60 90 120 150 180 210 240 270 Height 0. 5 0. 707 0. 866 1 0. 866 0. 5 0 -0. 5 -0. 866 -1 y 300 330 360 � Find the height at 300 degrees. x 300° 1 y 0. 5 cos -0. 866 correc -1. 000 radi -1. 732 tan

Easy Now… �Remember our Trigonometric ratios and think about what we were given. T S O H C A H i n e p p o s i t e y p o t e n u s e o s i n e d j a c e n t y p o t e n u s e a n g e n t O A p d p j o a s c i e t n e t

Right Plan But Watch Out!! �While your idea is flawless and you did correctly solve this, you did it for radians and not degrees. �There are two popular ways to measure angles- degrees is one, radians is the other �Whenever you are working with trigonometric functions- sine, cosine, tangent - you need to make sure your calculator is in the right MODE Help with switching you calculator Try again

Calculator Help �For the TI-81 through TI-84 the radian/degree shift is in the “mode” menu. The button is next to the 2 nd key. �For the TI-n. Spire the radian/degree shift is in the general settings menu �Many scientific calculators have a units shift button. On the screen it will say either “deg” or “rad” in little letters.

Let’s Use it!! Angle 30 45 60 90 120 150 180 210 240 270 300 Height 0. 5 0. 707 0. 866 1 0. 866 0. 5 0 -0. 5 -0. 866 -1 -0. 866 y 330 360 � Find the height at 330 degrees. x 330° 1 y -0. 5 correct 0. 866 cos -0. 577 tan -0. 132 radin

Easy Now… �Remember our Trigonometric ratios and think about what we were given. T S O H C A H i n e p p o s i t e y p o t e n u s e o s i n e d j a c e n t y p o t e n u s e a n g e n t O A p d p j o a s c i e t n e t

Right Plan But Watch Out!! �While your idea is flawless and you did correctly solve this, you did it for radians and not degrees. �There are two popular ways to measure angles- degrees is one, radians is the other �Whenever you are working with trigonometric functions- sine, cosine, tangent - you need to make sure your calculator is in the right MODE Help with switching you calculator Try again

Calculator Help �For the TI-81 through TI-84 the radian/degree shift is in the “mode” menu. The button is next to the 2 nd key. �For the TI-n. Spire the radian/degree shift is in the general settings menu �Many scientific calculators have a units shift button. On the screen it will say either “deg” or “rad” in little letters.
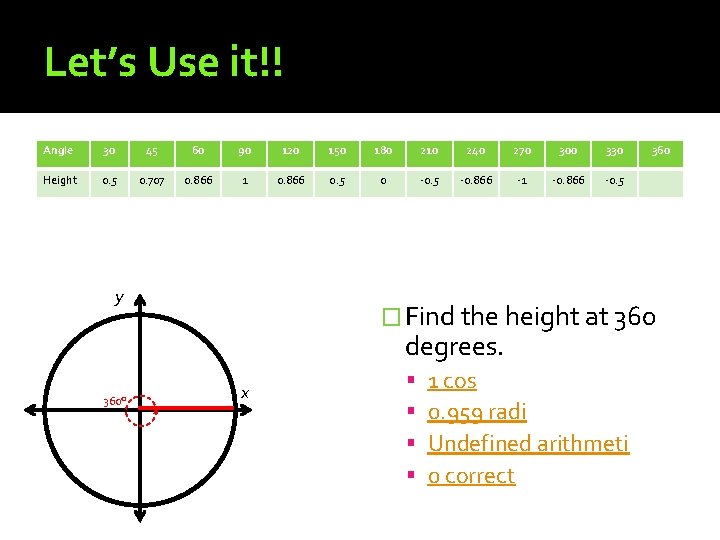
Let’s Use it!! Angle 30 45 60 90 120 150 180 210 240 270 300 330 Height 0. 5 0. 707 0. 866 1 0. 866 0. 5 0 -0. 5 -0. 866 -1 -0. 866 -0. 5 y � Find the height at 360 degrees. 360° 360 x 1 cos 0. 959 radi Undefined arithmeti 0 correct

Easy Now… �Remember our Trigonometric ratios and think about what we were given. T S O H C A H i n e p p o s i t e y p o t e n u s e o s i n e d j a c e n t y p o t e n u s e a n g e n t O A p d p j o a s c i e t n e t

Right Plan But Watch Out!! �While your idea is flawless and you did correctly solve this, you did it for radians and not degrees. �There are two popular ways to measure angles- degrees is one, radians is the other �Whenever you are working with trigonometric functions- sine, cosine, tangent - you need to make sure your calculator is in the right MODE Help with switching you calculator Try again

Calculator Help �For the TI-81 through TI-84 the radian/degree shift is in the “mode” menu. The button is next to the 2 nd key. �For the TI-n. Spire the radian/degree shift is in the general settings menu �Many scientific calculators have a units shift button. On the screen it will say either “deg” or “rad” in little letters.

Outstanding!! �Whew!! Now that we have created a great table we need to graph it. �But first… �Look back at your calculations. Did you notice any commonalities? Nope. I did not recognize nuttin’. Now that you mention it, I do notice that we did a lot of sine of the angle. Uh- duh? ! Of course! We did the same trigonometric ratio every single time. In fact, I stopped writing it out after the first four because I am awesome!

Interesting… �Look closely at each of the times you calculated the height. Every single time you were given an angle, the hypotenuse and you needed to find the opposite side. �Angle… opposite… hypotenuse Let’s try that question again.

Great Observation!! �Good job recognizing the pattern!! �This means that ANYTIME you need to find ANY height for ANY Megaloop evacuation you will ALWAYS use sin(Θ) Let’s get graphing this!!
Graphing �Now that we have a table we can create the graph.
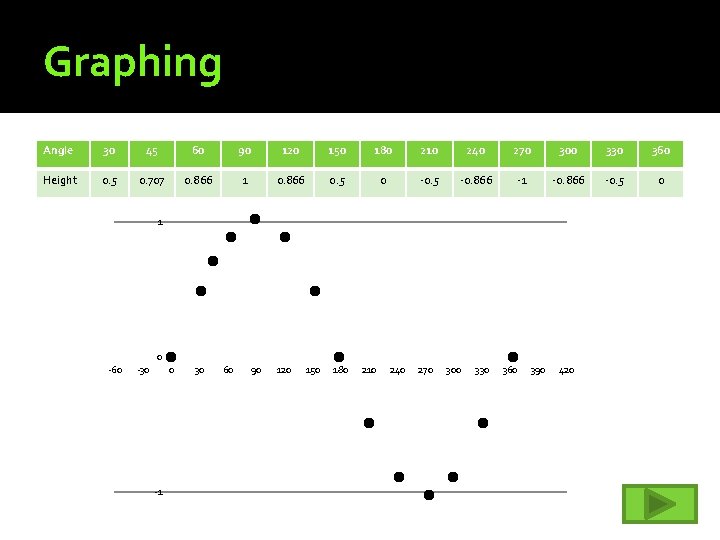
Graphing Angle 30 45 60 90 120 150 180 210 240 270 300 330 360 Height 0. 5 0. 707 0. 866 1 0. 866 0. 5 0 -0. 5 -0. 866 -1 -0. 866 -0. 5 0 1 0 -60 -30 0 -1 30 60 90 120 150 180 210 240 270 300 330 360 390 420

Congratulations!!! �You have just created your first graph of a trigonometric function. �This wave function you created is the graph of f(x)= sin(x). This is the parent equation for the sinusoidal family of functions. �We used the unit circle to generate this graph. �This means that for the Super Megaloop designer who wants to place half of the ride underground. She simply needs to remember sin(x) to know all the evacuation heights!!

Real World Applications �This wave function lends itself to many real world uses. �Pendulums, light, sound, and most circle motion can be graphed by these wave functions. �Specific features and transformations will be discussed later.
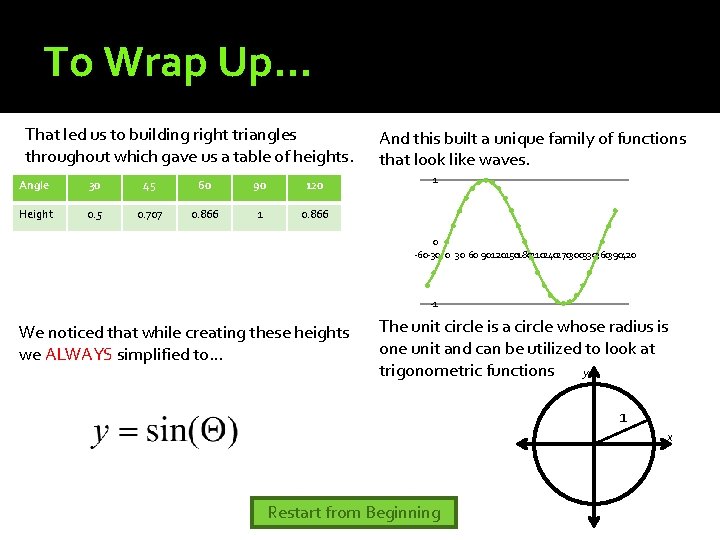
To Wrap Up… That led us to building right triangles throughout which gave us a table of heights. Angle 30 45 60 90 120 Height 0. 5 0. 707 0. 866 1 0. 866 And this built a unique family of functions that look like waves. 1 0 -60 -30 0 30 60 90120150180210240270300330360390420 -1 We noticed that while creating these heights we ALWAYS simplified to… The unit circle is a circle whose radius is one unit and can be utilized to look at trigonometric functions y 1 x Restart from Beginning
- Slides: 100