Trigonometry of Right Triangles Copyright Cengage Learning All













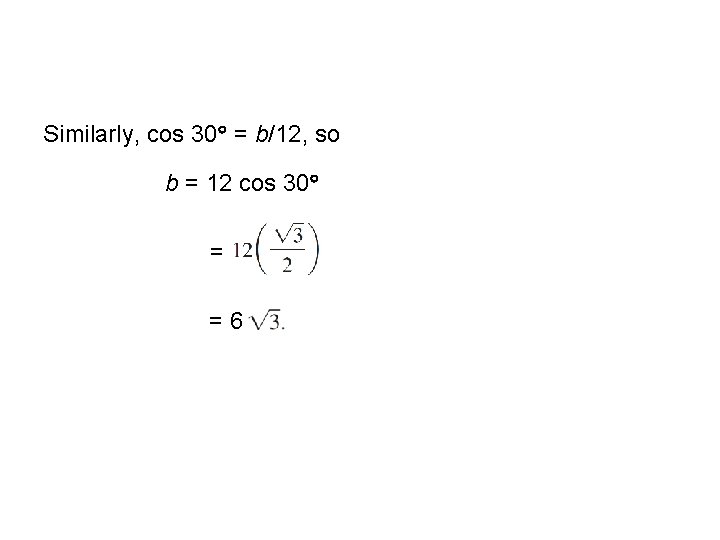











- Slides: 45

Trigonometry of Right Triangles Copyright © Cengage Learning. All rights reserved.

Objectives ► Trigonometric Ratios ► Special Triangles ► Applications of Trigonometry of Right Triangles

Trigonometric Ratios

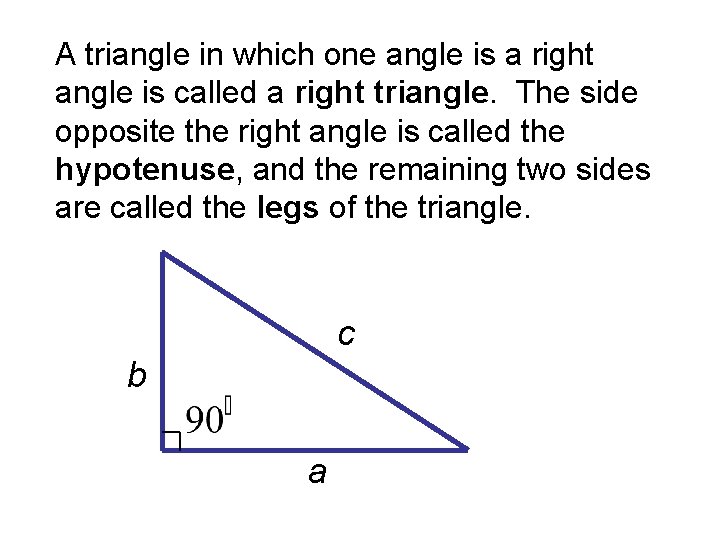
A triangle in which one angle is a right angle is called a right triangle. The side opposite the right angle is called the hypotenuse, and the remaining two sides are called the legs of the triangle. c b a

y P = (a, b) c b a x

a n i m e d i l s r e T Initial side

c a b

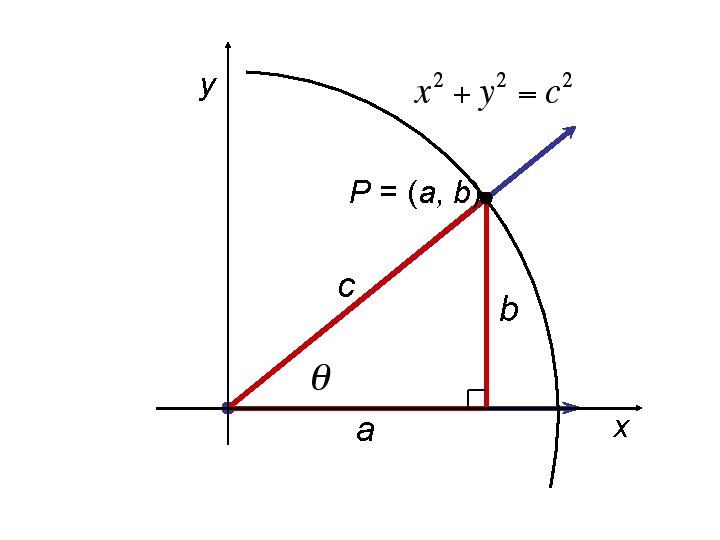
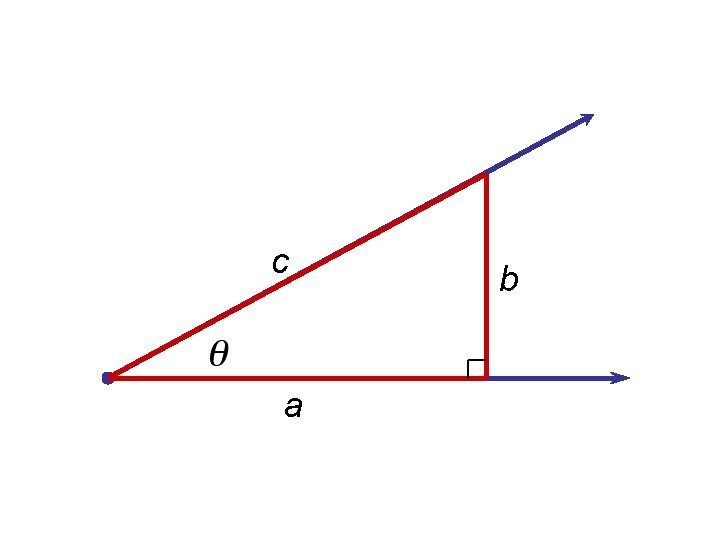
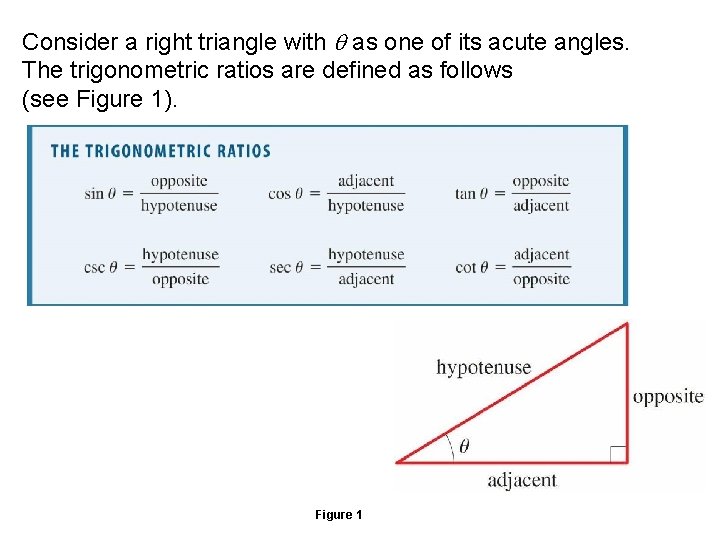
Consider a right triangle with as one of its acute angles. The trigonometric ratios are defined as follows (see Figure 1). Trigonometric Ratios Figure 1

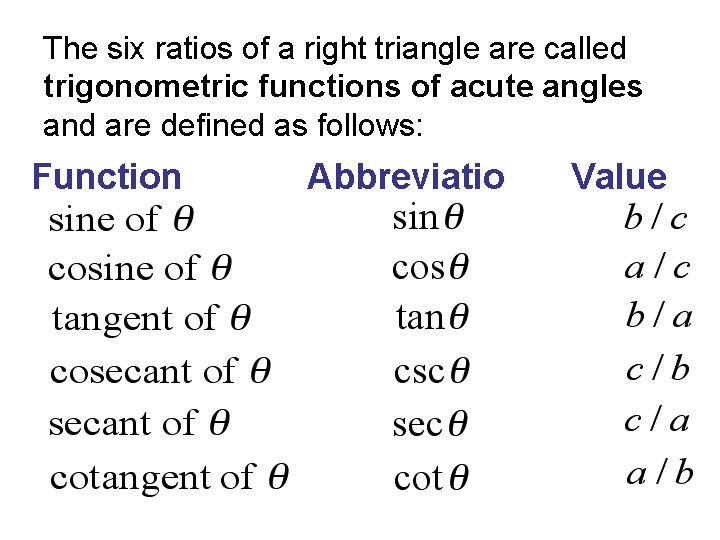
The six ratios of a right triangle are called trigonometric functions of acute angles and are defined as follows: Function name Abbreviatio n Value

The symbols we use for these ratios are abbreviations for their full names: sine, cosine, tangent, cosecant, cotangent. Trigonometric Ratios Since any two right triangles with angle are similar, these ratios are the same, regardless of the size of the triangle; the trigonometric ratios depend only on the angle (see Figure 2). sin = Figure 2 sin =

Example 1 – Finding Trigonometric Ratios Find the six trigonometric ratios of the angle in Figure 3. Solution: Figure 3

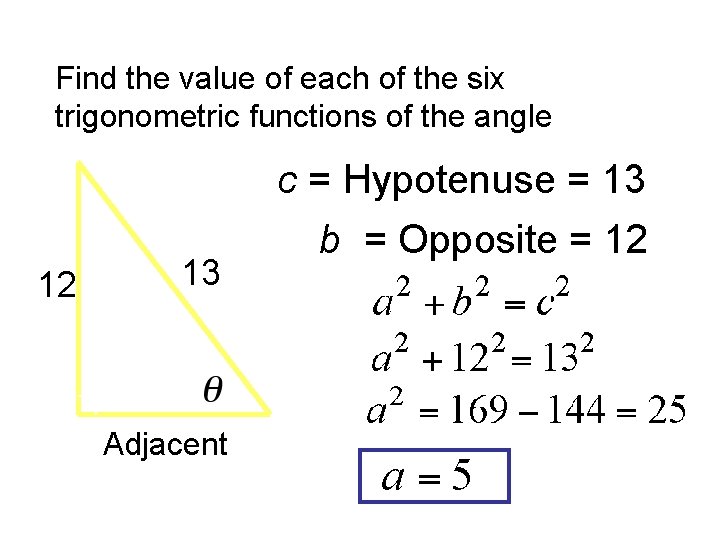
Find the value of each of the six trigonometric functions of the angle 12 13 Adjacent c = Hypotenuse = 13 b = Opposite = 12


Special Triangles

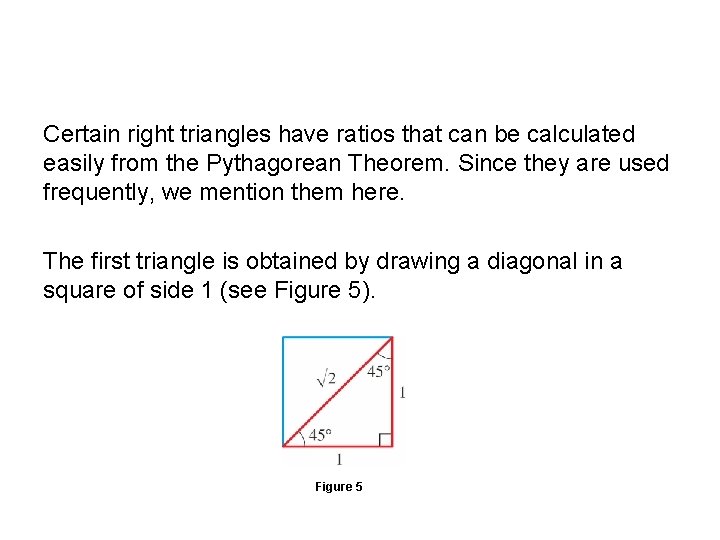
Special Triangles Certain right triangles have ratios that can be calculated easily from the Pythagorean Theorem. Since they are used frequently, we mention them here. The first triangle is obtained by drawing a diagonal in a square of side 1 (see Figure 5). Figure 5

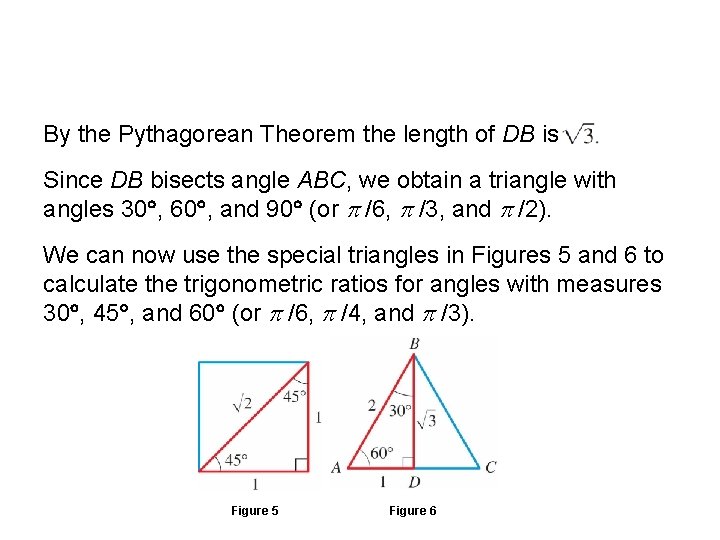
Special Triangles By the Pythagorean Theorem this diagonal has length . The resulting triangle has angles 45 , and 90 (or /4, and /2). To get the second triangle, we start with an equilateral triangle ABC of side 2 and draw the perpendicular bisector DB of the base, as in Figure 6

Special Triangles By the Pythagorean Theorem the length of DB is Since DB bisects angle ABC, we obtain a triangle with angles 30 , 60 , and 90 (or /6, /3, and /2). We can now use the special triangles in Figures 5 and 6 to calculate the trigonometric ratios for angles with measures 30 , 45 , and 60 (or /6, /4, and /3). Figure 5 Figure 6

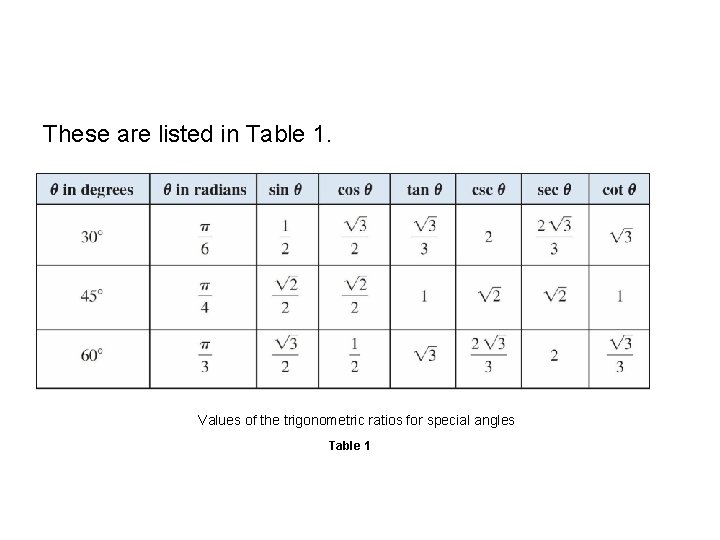
Special Triangles These are listed in Table 1. Values of the trigonometric ratios for special angles Table 1

Special Triangles To find the values of the trigonometric ratios for other angles, we use a calculator. Mathematical methods (called numerical methods) used in finding the trigonometric ratios are programmed directly into scientific calculators. Calculators give the values of sine, cosine, and tangent; the other ratios can be easily calculated from these by using the following reciprocal relations:

Special Triangles We follow the convention that when we write sin t, we mean the sine of the angle whose radian measure is t. For instance, sin 1 means the sine of the angle whose radian measure is 1. When using a calculator to find an approximate value for this number, set your calculator to radian mode; you will find that sin 1 0. 841471 If you want to find the sine of the angle whose measure is 1 , set your calculator to degree mode; you will find that sin 1 0. 0174524

BELL RINGER Complete the unit circle - Degrees - Cosine & Sine Values on the outside

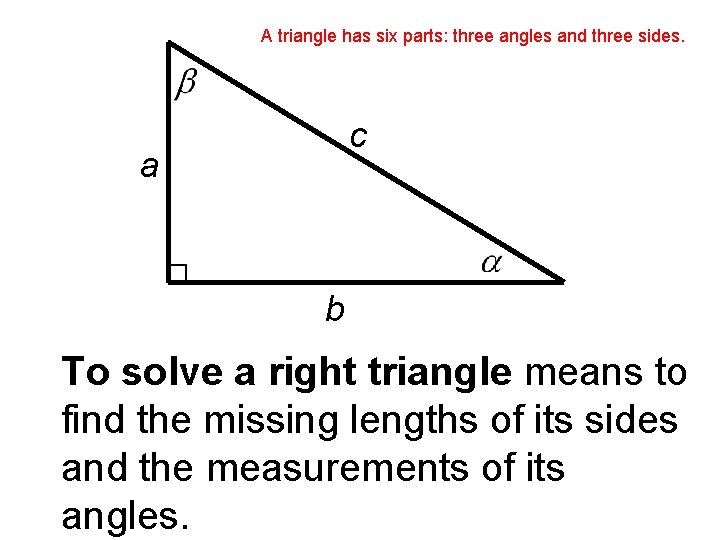
A triangle has six parts: three angles and three sides. c a b To solve a right triangle means to find the missing lengths of its sides and the measurements of its angles.

Applications of Trigonometry of Right Triangles To solve a triangle means to determine all of its parts from the information known about the triangle, that is, to determine the lengths of the three sides and the measures of the three angles.

Example 3 – Solving a Right Triangle Solve triangle ABC, shown in Figure 7 Solution: It’s clear that B = 60. To find a, we look for an equation that relates a to the lengths and angles we already know. In this case, we have sin 30 = a/12, so a = 12 sin 30 = = 6
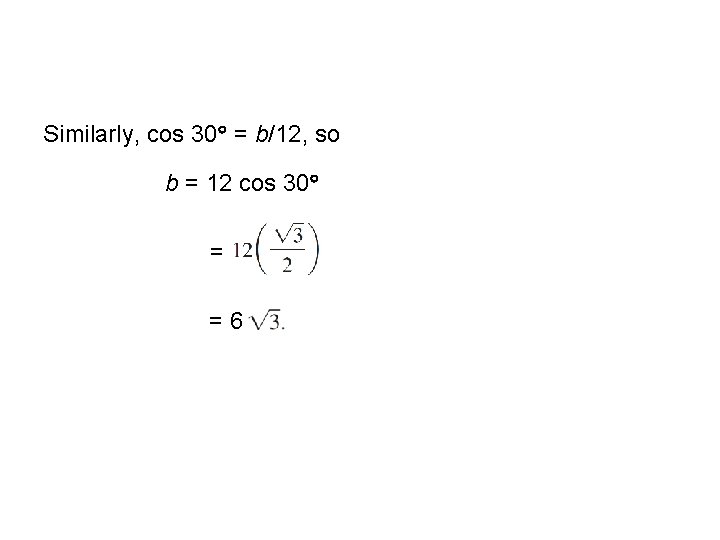
Example 3 – Solution Similarly, cos 30 = b/12, so b = 12 cos 30 = = 6 cont’d

c 4 b

Inverse Trig Functions What if you know all the sides of a right triangle but you don’t know the other 2 angle measures. How could you find these angle measures? • Think of the angle measure as a present. When you take the sine, cosine, or tangent of that angle, it is similar to wrapping your present. • The inverse trig functions give you the ability to unwrap your present and to find the value of the angle in question.

Notation A=sin-1(z) is read as the inverse sine of A. Never think of the -1 as an exponent. It may look like an exponent and thus you might think it is 1/sin(z), this is not true. (We refer to 1/sin(z) as the cosecant of z) A=cos-1(z) is read as the inverse cosine of A. A=tan-1(z) is read as the inverse tangent of A.

Inverse Trig definitions Referring to the right triangle from the introduction slide. The inverse trig functions are defined as follows: A=sin-1(opp/hyp) A=cos-1(adj/hyp) A=tan-1(opp/adj)

Example using inverse trig functions Find the angles A and B given the following right triangle. • Find angle A. • Use an inverse trig function to find A. For instance A=sin-1(6/10)=36. 9°. Then B = 180° - 90° - 36. 9° = 53. 1°. B 6 10 8 A

Applications of Trigonometry of Right Triangles

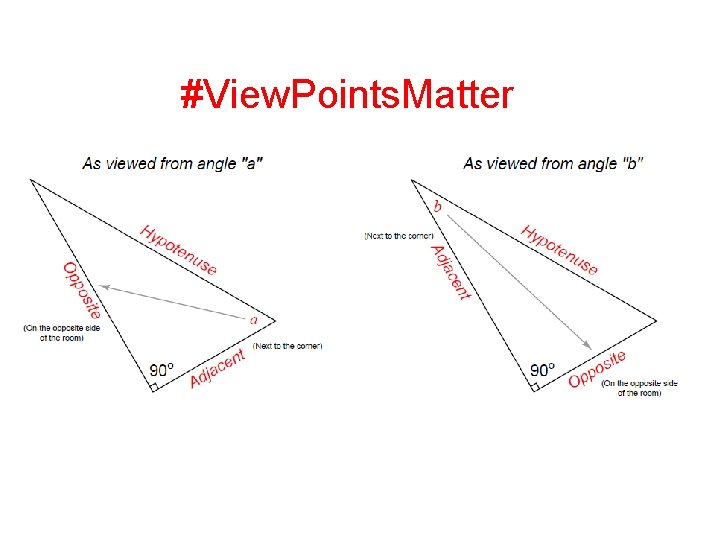
#View. Points. Matter


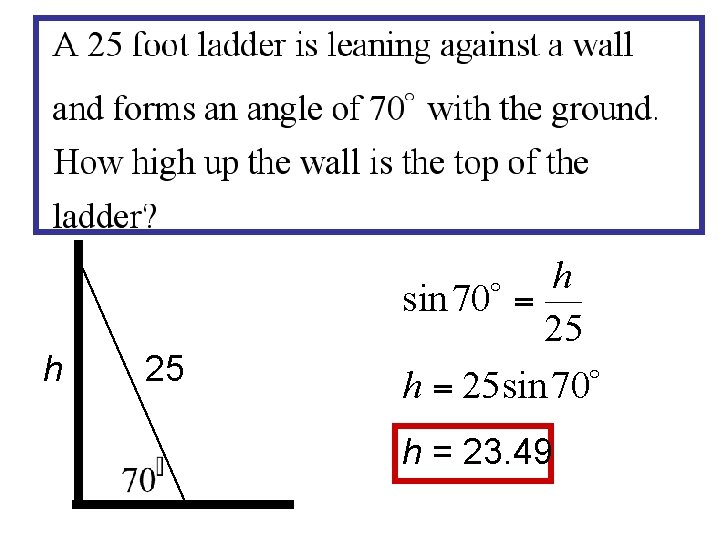
h 25 h = 23. 49

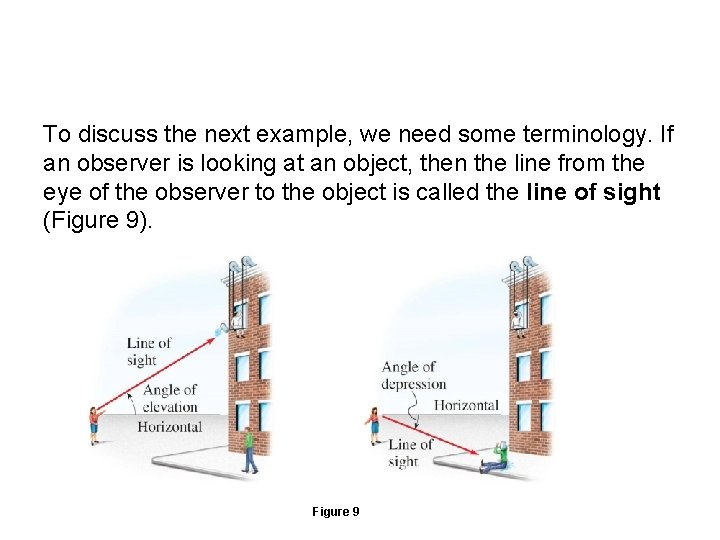
Applications of Trigonometry of Right Triangles To discuss the next example, we need some terminology. If an observer is looking at an object, then the line from the eye of the observer to the object is called the line of sight (Figure 9). Figure 9

Applications of Trigonometry of Right Triangles If the object being observed is above the horizontal, then the angle between the line of sight and the horizontal is called the angle of elevation. If the object is below the horizontal, then the angle between the line of sight and the horizontal is called the angle of depression. If the line of sight follows a physical object, such as an inclined plane or a hillside, we use the term angle of inclination.

Example 4 – Finding the Height of a Tree A giant redwood tree casts a shadow 532 ft long. Find the height of the tree if the angle of elevation of the sun is 25. 7. Solution: Let the height of the tree be h. From Figure 10 we see that Definition of tangent Figure 10

Example 4 – Solution cont’d h = 532 tan 25. 7 Multiply by 532 = 532(0. 48127) Use a calculator 256 Therefore, the height of the tree is about 256 ft.

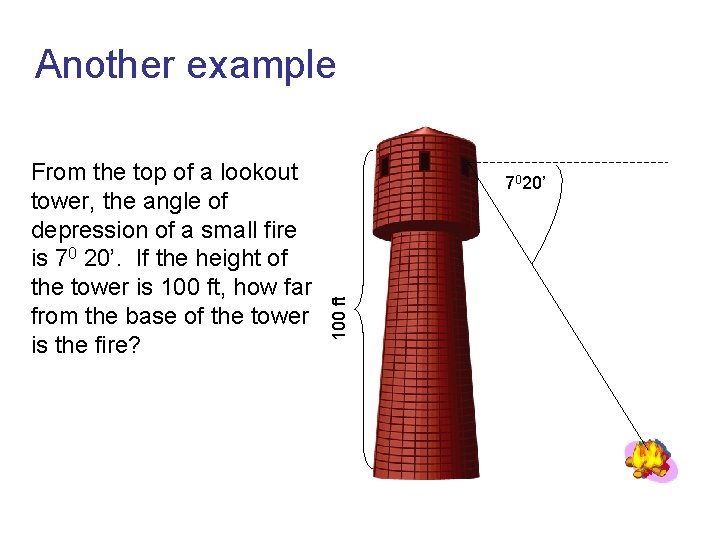
Another example 7020’ 100 ft From the top of a lookout tower, the angle of depression of a small fire is 70 20’. If the height of the tower is 100 ft, how far from the base of the tower is the fire?

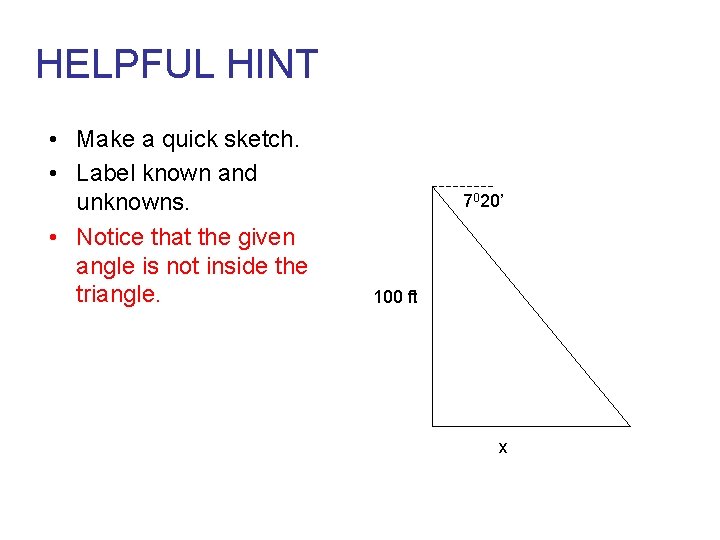
HELPFUL HINT • Make a quick sketch. • Label known and unknowns. • Notice that the given angle is not inside the triangle. 7020’ 100 ft x

If a ladder, 8 feet long, is placed so that it just reaches a window 6 feet from the ground, how far from the building is the foot of the ladder?

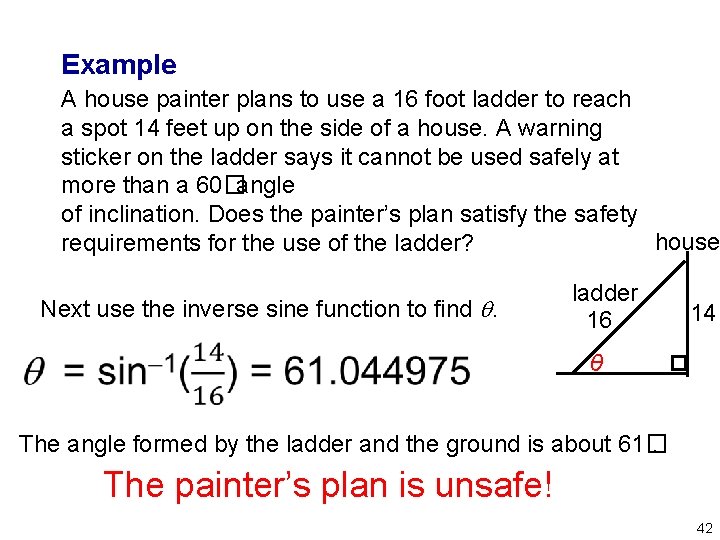
Example A house painter plans to use a 16 foot ladder to reach a spot 14 feet up on the side of a house. A warning sticker on the ladder says it cannot be used safely at more than a 60� angle of inclination. Does the painter’s plan satisfy the safety house requirements for the use of the ladder? Next use the inverse sine function to find . ladder 16 14 θ The angle formed by the ladder and the ground is about 61�. The painter’s plan is unsafe! 42

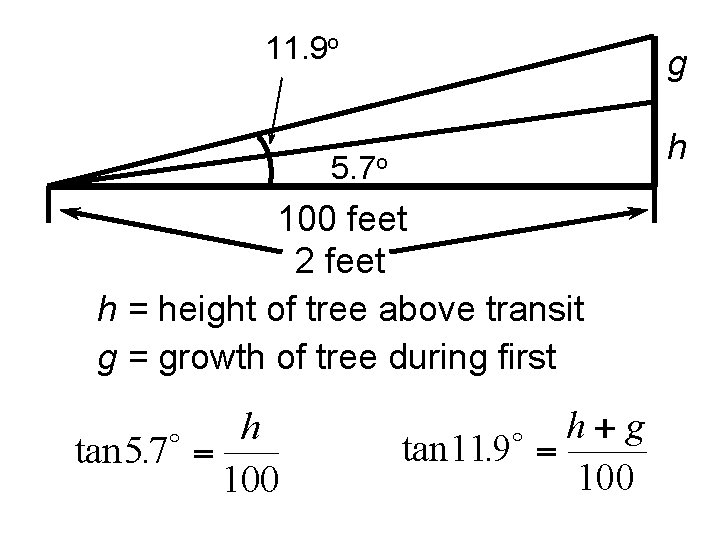
Yola just planted a Hybrid Elm. The nursery claims the tree grows 12 feet per year. Yola wants to verify the claim. She walks 100 feet from the base of the tree and, using a transit that is 2 feet off the ground, determines the angle of elevation is 5. 7 o. One year later, the angle of elevation 100 feet from the tree is 11. 9 o. Is the nursery’s claim true?

11. 9 o 5. 7 o 100 feet 2 feet h = height of tree above transit g = growth of tree during first year g h

Height of tree after 1 year: 2 + 9. 98 + 11. 09 = 23. 07 feet