Inversesofof Trigonometric 13 4 Functions 13 4 Functions

Inversesofof. Trigonometric 13 -4 Functions 13 -4 Functions Warm Up Lesson Presentation Lesson Quiz Holt Algebra 22

Inverses of Trigonometric 13 -4 Functions Objectives Evaluate inverse trigonometric functions. Use trigonometric equations and inverse trigonometric functions to solve problems. Holt Algebra 2

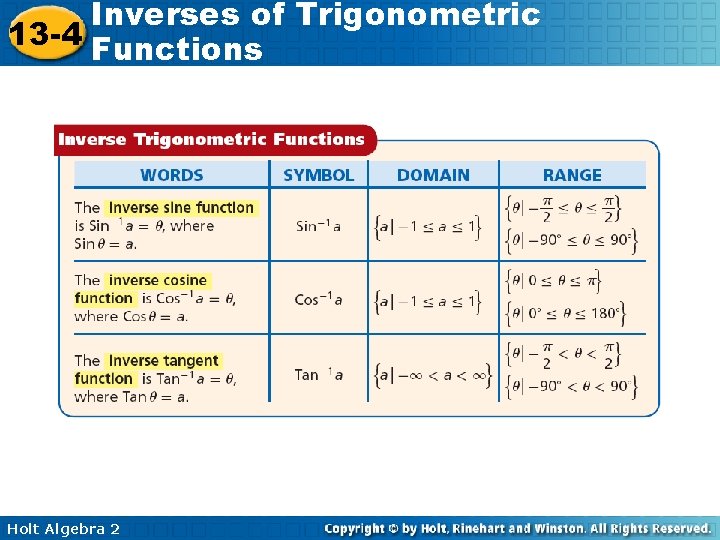
Inverses of Trigonometric 13 -4 Functions Vocabulary inverse sine functions inverse cosine function inverse tangent function Holt Algebra 2

Inverses of Trigonometric 13 -4 Functions You have evaluated trigonometric functions for a given angle. You can also find the measure of angles given the value of a trigonometric function by using an inverse trigonometric relation. Holt Algebra 2

Inverses of Trigonometric 13 -4 Functions Reading Math The expression sin-1 is read as “the inverse sine. ” In this notation, -1 indicates the inverse of the sine function, NOT the reciprocal of the sine function. Holt Algebra 2

Inverses of Trigonometric 13 -4 Functions The inverses of the trigonometric functions are not functions themselves because there are many values of θ for a particular value of a. For example, suppose that you want to find cos-1 . Based on the unit circle, angles that measure and have a cosine of radians . So do all angles that are coterminal with these angles. Holt Algebra 2

Inverses of Trigonometric 13 -4 Functions Example 1: Finding Trigonometric Inverses Find all possible values of cos-1 Step 1 Find the values between 0 and 2 radians for which cos θ is equal to. Use the x-coordinates of points on the unit circle. Holt Algebra 2 .

Inverses of Trigonometric 13 -4 Functions Example 1 Continued Find all possible values of cos-1 . Step 2 Find the angles that are coterminal with angles measuring and radians. Add integer multiples of 2 radians, where n is an integer Holt Algebra 2

Inverses of Trigonometric 13 -4 Functions Check It Out! Example 1 Find all possible values of tan-11. Holt Algebra 2

Inverses of Trigonometric 13 -4 Functions Because more than one value of θ produces the same output value for a given trigonometric function, it is necessary to restrict the domain of each trigonometric function in order to define the inverse trigonometric functions. Holt Algebra 2

Inverses of Trigonometric 13 -4 Functions Trigonometric functions with restricted domains are indicated with a capital letter. The domains of the Sine, Cosine, and Tangent functions are restricted as follows. Sinθ = sinθ for {θ| } θ is restricted to Quadrants I and IV. Cosθ = cosθ for {θ| } θ is restricted to Quadrants I and II. Tanθ = tanθ for {θ| } θ is restricted to Quadrants I and IV. Holt Algebra 2

Inverses of Trigonometric 13 -4 Functions These functions can be used to define the inverse trigonometric functions. For each value of a in the domain of the inverse trigonometric functions, there is only one value of θ. Therefore, even though tan-1 has many values, Tan-11 has only one value. Holt Algebra 2

Inverses of Trigonometric 13 -4 Functions Holt Algebra 2

Inverses of Trigonometric 13 -4 Functions Reading Math The inverse trigonometric functions are also called the arcsine, arccosine, and arctangent functions. Holt Algebra 2

Inverses of Trigonometric 13 -4 Functions Example 2 A: Evaluating Inverse Trigonometric Functions Evaluate each inverse trigonometric function. Give your answer in both radians and degrees. Find value of θ for or whose Cosine. Use x-coordinates of points on the unit circle. Holt Algebra 2

Inverses of Trigonometric 13 -4 Functions Example 2 B: Evaluating Inverse Trigonometric Functions Evaluate each inverse trigonometric function. Give your answer in both radians and degrees. The domain of the inverse sine function is {a|1 = – 1 ≤ a ≤ 1}. Because is outside this domain. Sin-1 is undefined. Holt Algebra 2

Inverses of Trigonometric 13 -4 Functions Check It Out! Example 2 a Evaluate each inverse trigonometric function. Give your answer in both radians and degrees. Holt Algebra 2

Inverses of Trigonometric 13 -4 Functions Check It Out! Example 2 b Evaluate each inverse trigonometric function. Give your answer in both radians and degrees. Holt Algebra 2

Inverses of Trigonometric 13 -4 Functions Example 3: Safety Application A painter needs to lean a 30 ft ladder against a wall. Safety guidelines recommend that the distance between the base of the ladder and the wall should be of the length of the ladder. To the nearest degree, what acute angle should the ladder make with the ground? Holt Algebra 2

Inverses of Trigonometric 13 -4 Functions Example 3 Continued Step 1 Draw a diagram. The base of the ladder should be (30) = 7. 5 ft from the wall. The angle between the ladder and the ground θ is the measure of an acute angle of a right triangle. 7. 5 Holt Algebra 2 θ

Inverses of Trigonometric 13 -4 Functions Example 3 Continued Step 2 Find the value of θ. Use the cosine ratio. Substitute 7. 5 for adj. and 30 for hyp. Then simplify. The angle between the ladder and the ground should be about 76° Holt Algebra 2

Inverses of Trigonometric 13 -4 Functions Check It Out! Example 3 A group of hikers wants to walk form a lake to an unusual rock formation. The formation is 1 mile east and 0. 75 mile north of the lake. To the nearest degree, in what direction should the hikers head from the lake to reach the rock formation? Rock 0. 75 mi θ Lake Holt Algebra 2 1 mi

Inverses of Trigonometric 13 -4 Functions Example 4 A: Solving Trigonometric Equations Solve each equation to the nearest tenth. Use the given restrictions. sin θ = 0. 4, for – 90° ≤ θ ≤ 90° The restrictions on θ are the same as those for the inverse sine function. = Sin-1(0. 4) ≈ 23. 6° Holt Algebra 2 Use the inverse sine function on your calculator.

Inverses of Trigonometric 13 -4 Functions Example 4 B: Solving Trigonometric Equations Solve each equation to the nearest tenth. Use the given restrictions. sin θ = 0. 4, for 90° ≤ θ ≤ 270° The terminal side of θ is restricted to Quadrants ll and lll. Since sin θ > 0, find the angle in Quadrant ll that has the same sine value as 23. 6°. θ has a reference angle of 23. 6°, and θ ≈ 180° – 23. 6° ≈ 156. 4° 90° < θ < 180°. Holt Algebra 2

Inverses of Trigonometric 13 -4 Functions Check It Out! Example 4 a Solve each equations to the nearest tenth. Use the given restrictions. tan θ = – 2, for – 90° < θ < 90° Holt Algebra 2

Inverses of Trigonometric 13 -4 Functions Check It Out! Example 4 b Solve each equations to the nearest tenth. Use the given restrictions. tan θ = – 2, for 90° < θ < 180° Holt Algebra 2