Lesson 15 Trigonometric Ratios The Trigonometric Functions we

Lesson 15: Trigonometric Ratios

The Trigonometric Functions we will be looking at SINE COSINE TANGENT

The Trigonometric Functions SINE COSINE TANGENT

SINE Pronounced “sign”

COSINE Pronounced “co-sign”

TANGENT Pronounced “tan-gent”

Greek Letter Prounounced “theta” Represents an unknown angle

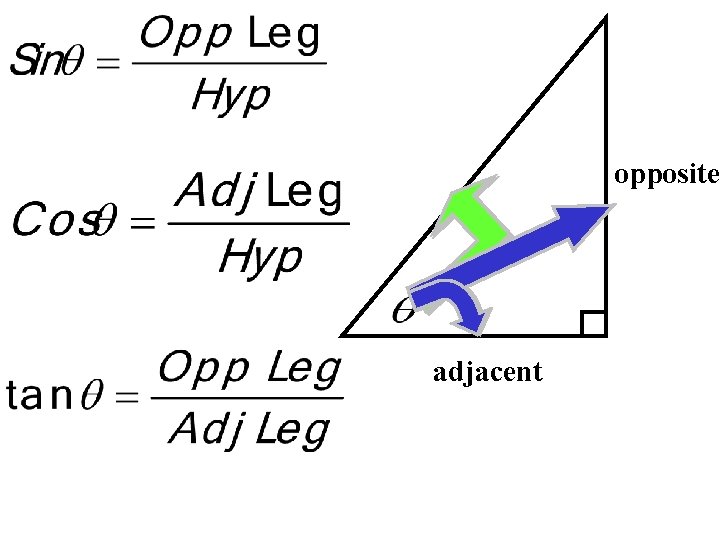
hypotenuse adjacent opposite

SOH-CAH-TOA S - Sine O - Opposite H – Hypotenuse C - Cosine A – Adjacent H – Hypotenuse T – Tangent O - Opposite A - Adjacent

Finding sin, cos, and tan. (Just writing a ratio. ) 1. Circle Angle. 2. Label sides (hyp, opp, adj) 3. Set up ratio

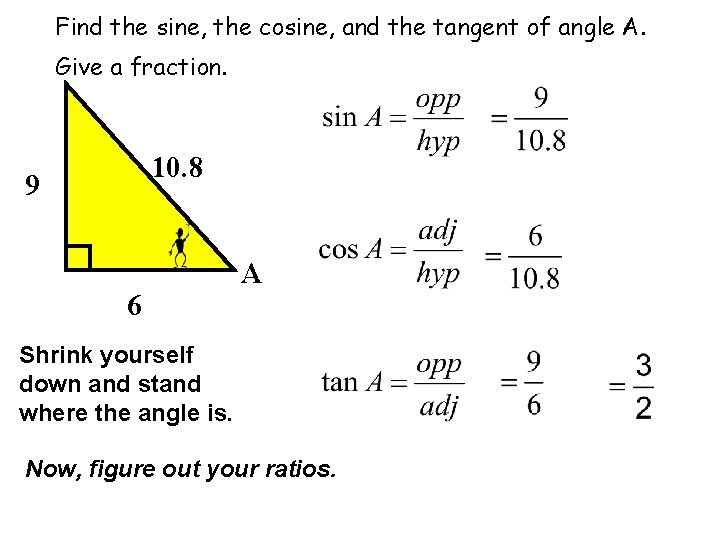
Find the sine, the cosine, and the tangent of angle A. Give a fraction. 10. 8 9 6 A Shrink yourself down and stand where the angle is. Now, figure out your ratios.

Find the sine, the cosine, and the tangent of angle A 24. 5 8. 2 A 23. 1 Shrink yourself down and stand where the angle is. Now, figure out your ratios.

1. Set up and calculate the trig ratios for sine, cosine and tangent of angle A. 2. Set up and calculate the trig ratios for sine, cosine and tangent of angle B.

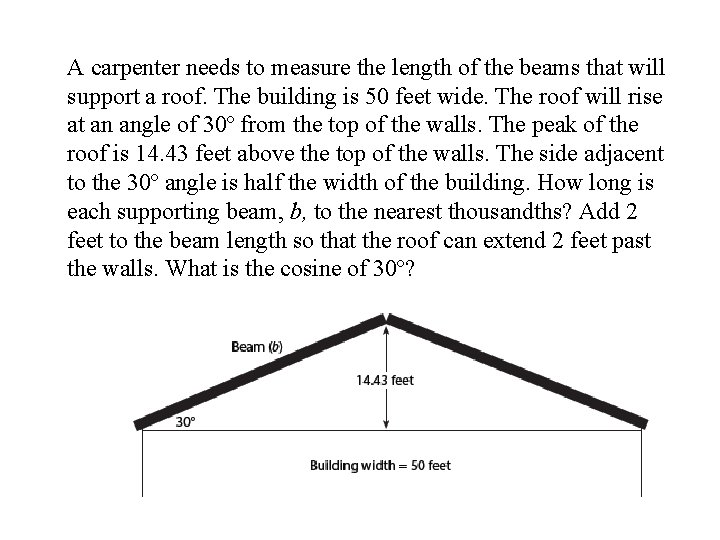
A carpenter needs to measure the length of the beams that will support a roof. The building is 50 feet wide. The roof will rise at an angle of 30º from the top of the walls. The peak of the roof is 14. 43 feet above the top of the walls. The side adjacent to the 30º angle is half the width of the building. How long is each supporting beam, b, to the nearest thousandths? Add 2 feet to the beam length so that the roof can extend 2 feet past the walls. What is the cosine of 30º?

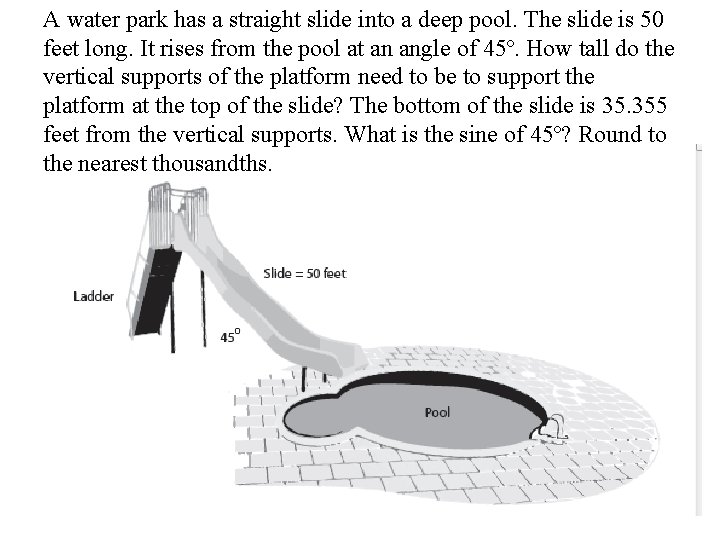
A water park has a straight slide into a deep pool. The slide is 50 feet long. It rises from the pool at an angle of 45º. How tall do the vertical supports of the platform need to be to support the platform at the top of the slide? The bottom of the slide is 35. 355 feet from the vertical supports. What is the sine of 45º? Round to the nearest thousandths.

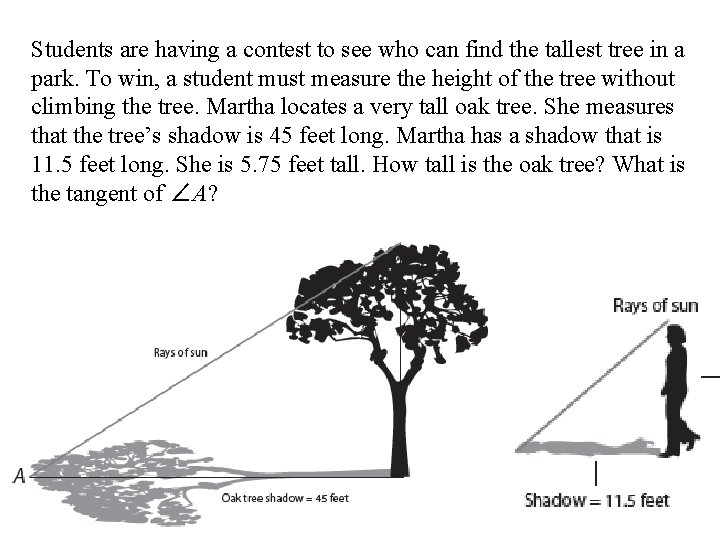
Students are having a contest to see who can find the tallest tree in a park. To win, a student must measure the height of the tree without climbing the tree. Martha locates a very tall oak tree. She measures that the tree’s shadow is 45 feet long. Martha has a shadow that is 11. 5 feet long. She is 5. 75 feet tall. How tall is the oak tree? What is the tangent of ∠A?

Lesson 15: Finding Missing Sides and Angles

Finding an angle. (Figuring out which ratio to use and an inverse trig button. ) 1. 2. 3. 4. Circle Angle. Label sides (hyp, opp, adj) Set up ratio Calculate using inverse trig

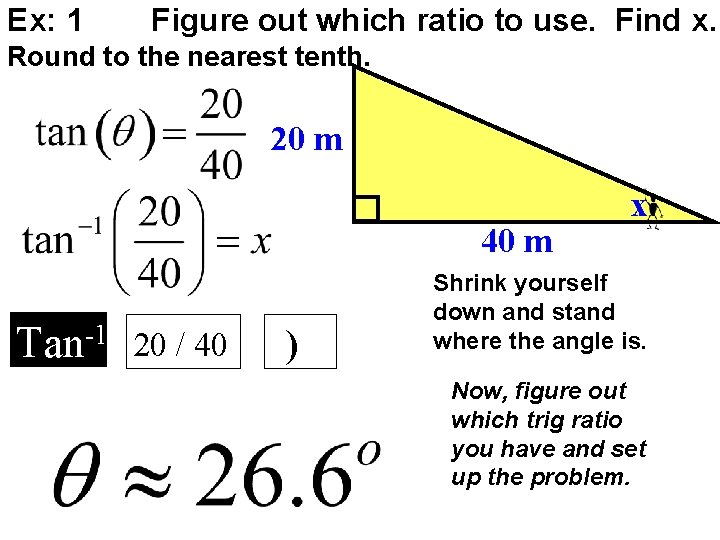
Ex: 1 Figure out which ratio to use. Find x. Round to the nearest tenth. 20 m 40 m Tan-1 20 / 40 ) x Shrink yourself down and stand where the angle is. Now, figure out which trig ratio you have and set up the problem.

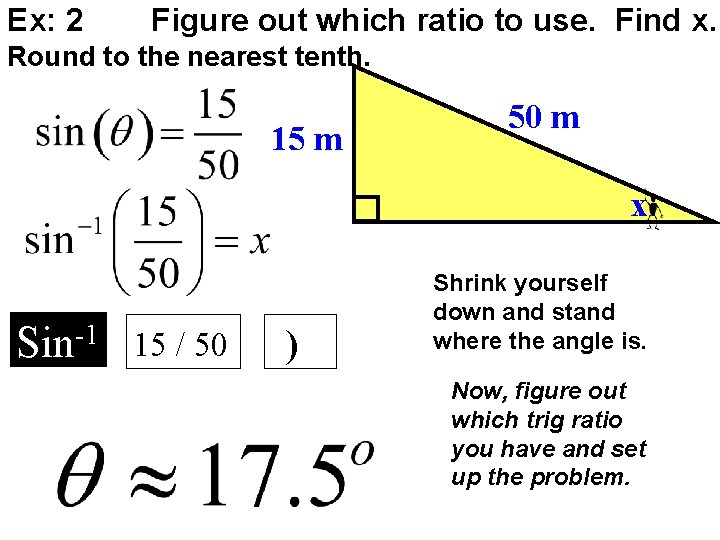
Ex: 2 Figure out which ratio to use. Find x. Round to the nearest tenth. 15 m 50 m x Sin-1 15 / 50 ) Shrink yourself down and stand where the angle is. Now, figure out which trig ratio you have and set up the problem.

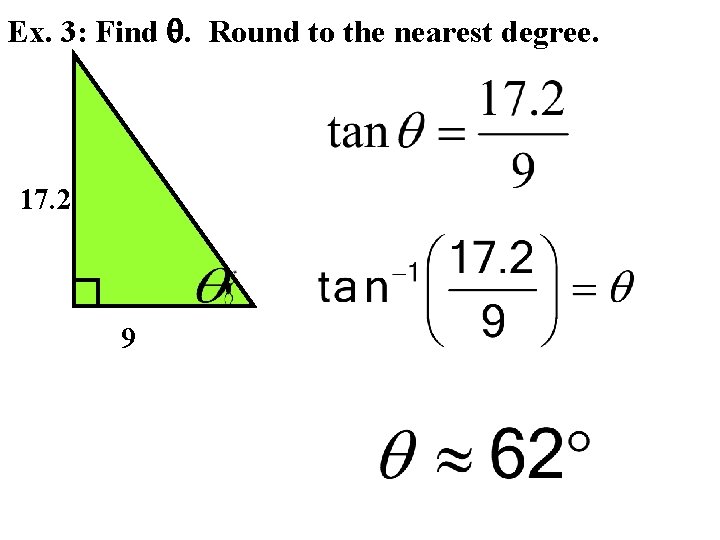
Ex. 3: Find . Round to the nearest degree. 17. 2 9

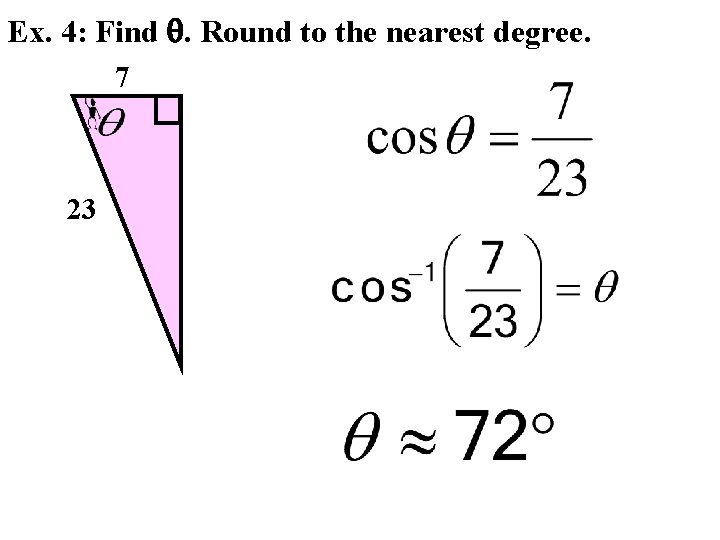
Ex. 4: Find . Round to the nearest degree. 7 23

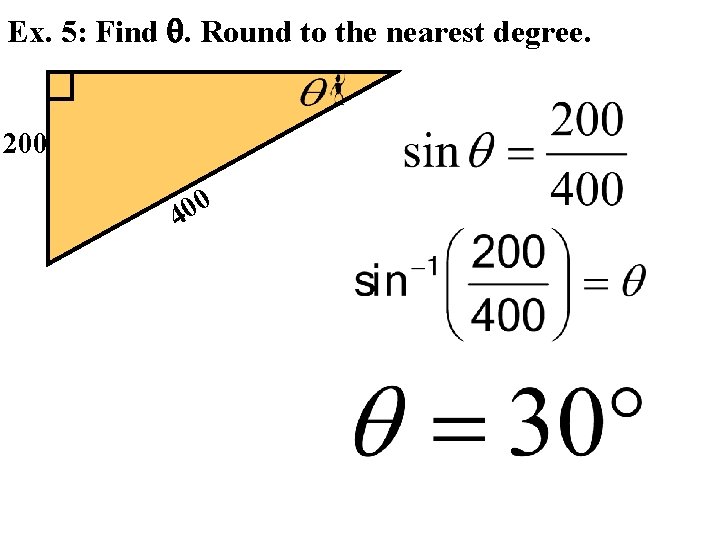
Ex. 5: Find . Round to the nearest degree. 200 0 0 4

Finding a side. (Figuring out which ratio to use and getting to use a trig button. ) 1. Circle Angle. 2. Label sides (hyp, opp, adj) 3. Set up ratio 4. Cross Multiply

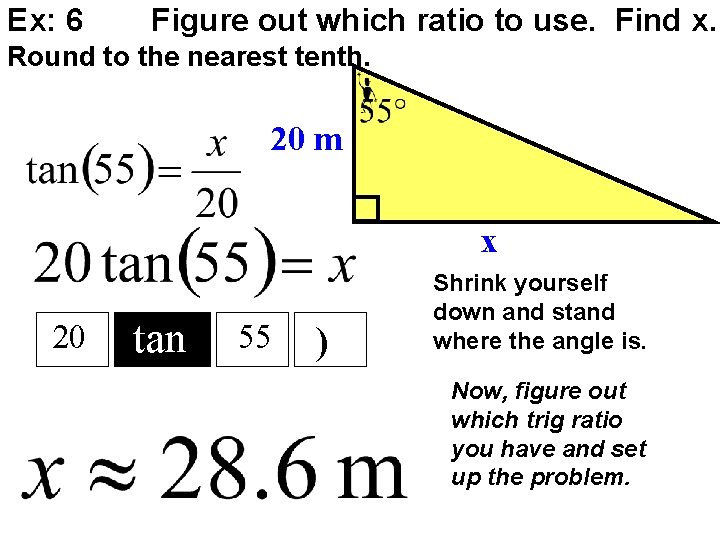
Ex: 6 Figure out which ratio to use. Find x. Round to the nearest tenth. 20 m x 20 tan 55 ) Shrink yourself down and stand where the angle is. Now, figure out which trig ratio you have and set up the problem.

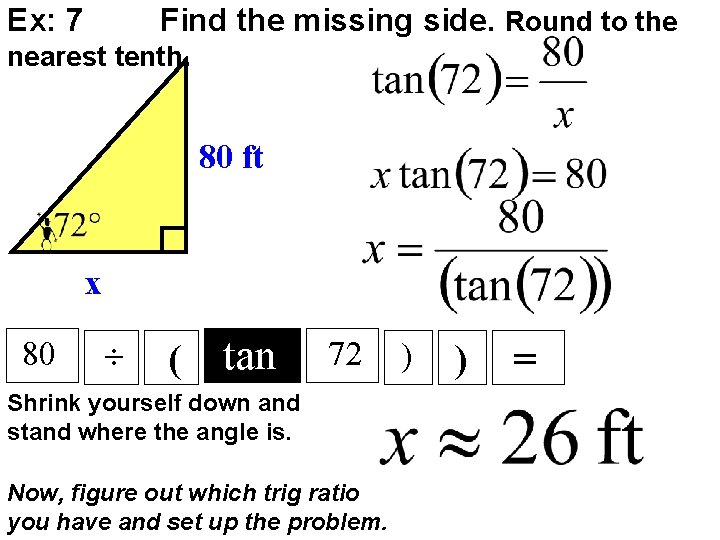
Ex: 7 Find the missing side. Round to the nearest tenth. 80 ft x 80 ( tan 72 Shrink yourself down and stand where the angle is. Now, figure out which trig ratio you have and set up the problem. ) ) =

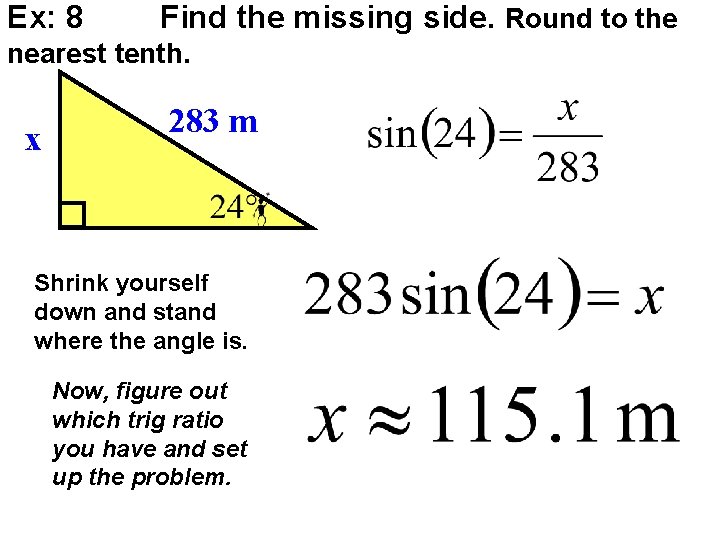
Ex: 8 Find the missing side. Round to the nearest tenth. x 283 m Shrink yourself down and stand where the angle is. Now, figure out which trig ratio you have and set up the problem.

Ex: 9 Find the missing side. Round to the nearest tenth. 20 ft x

When we are trying to find a side we use sin, cos, or tan. When we are trying to find an angle we use (INVERSE) sin -1, cos-1, or tan-1.