TRIGONOMETRIC RATIOS The Trigonometric Functions we will be

TRIGONOMETRIC RATIOS

The Trigonometric Functions we will be looking at SINE COSINE TANGENT

The Trigonometric Functions SINE COSINE TANGENT

SINE Prounounced “sign”

COSINE Prounounced “co-sign”

TANGENT Prounounced “tan-gent”

hypotenus e A adjacent opposite opposit

WE CAN USE TRIGONOMETRIC RATIOS TO FIND MISSING SIDES A B WHERE A IS THE ANGLE MEASUREMENT C

THE RATIOS CAN BE REMEMBERED BY THE SAYING hypotenuse A opposite adjacent

What is the sine ratio of A? What is the cosine ratio of A? What is the tangent ratio of A? A 10 8 B 6 C

Find the sine, the cosine, and the tangent of angle A. Give a fraction and decimal answer (round to 4 places). 10. 8 9 A 6

Find the values of the three trigonometric functions of . Pythagorean Theorem: (3)² + (4)² = c² 5 = c ? 5 4 3

Find the sine, the cosine, and the tangent of angle A B Give a fraction and decimal answer (round to 4 decimal places). 24. 5 8. 2 A 23. 1

HOW CAN WE USE THESE RATIOS TO FIND SIDE LENGTHS? A What is the length of BC? Ask yourself the following questions 22º ~What angle measurement do I have? 16 A ~From that angle what am I LOOKING FOR (adjacent, opposite or hypotenuse) OPPOSITE ~From the angle what do I HAVE? (adjacent, opposite or hypotenuse) HYPOTENUSE ~So which ratio should we use? SINE B C

HOW CAN WE USE THESE RATIOS TO FIND SIDE LENGTHS? A What is the length of BC? 22º 16 16 Sin 22 =x 5. 99=x B C

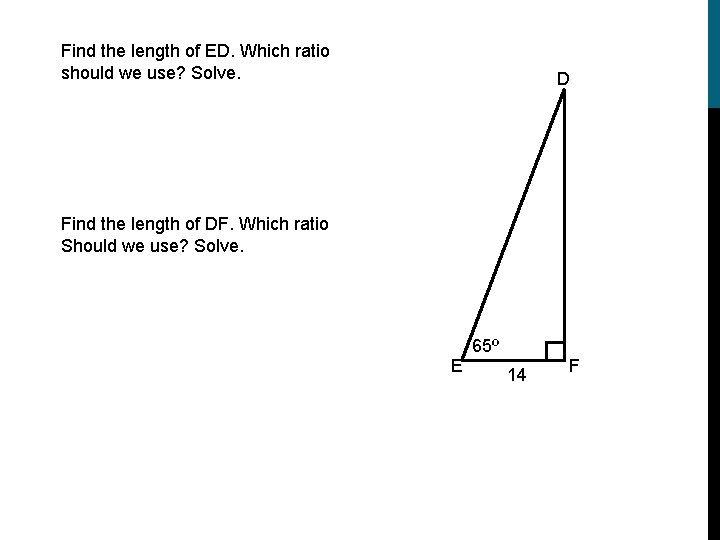
Find the length of ED. Which ratio should we use? Solve. D Find the length of DF. Which ratio Should we use? Solve. E 65º 14 F

FINDING AN ANGLE. (FIGURING OUT WHICH RATIO TO USE AND GETTING TO USE THE 2 ND BUTTON AND ONE OF THE TRIG BUTTONS. )

EX. 1: FIND . ROUND TO FOUR DECIMAL PLACES. nd 2 17. 2 tan 17. 2 9 Make sure you are in degree mode (not radian). 9

EX. 2: FIND . ROUND TO THREE DECIMAL PLACES. 7 23 nd 2 co s 7 Make sure you are in degree mode (not radian). 23

EX. 3: FIND . ROUND TO THREE DECIMAL PLACES. 200 0 0 4 nd 2 sin 200 Make sure you are in degree mode (not radian). 400

WHEN WE ARE TRYING TO FIND A SIDE WE USE SIN, COS, OR TAN. When we are trying to find an angle we use sin-1, cos-1, or tan-1.

SOLVE THE PROBLEM:

A ladder is leaning against a house so that the top of the ladder is 12 feet above the ground. The angle with the ground is 51º. How far is the base of the ladder from the house? 12 51º x

An angle of elevation is the angle formed by a horizontal line and a line of sight to a point above the line. In the diagram, 1 is the angle of elevation from the tower T to the plane P. An angle of depression is the angle formed by a horizontal line and a line of sight to a point below the line. 2 is the angle of depression from the plane to the tower.

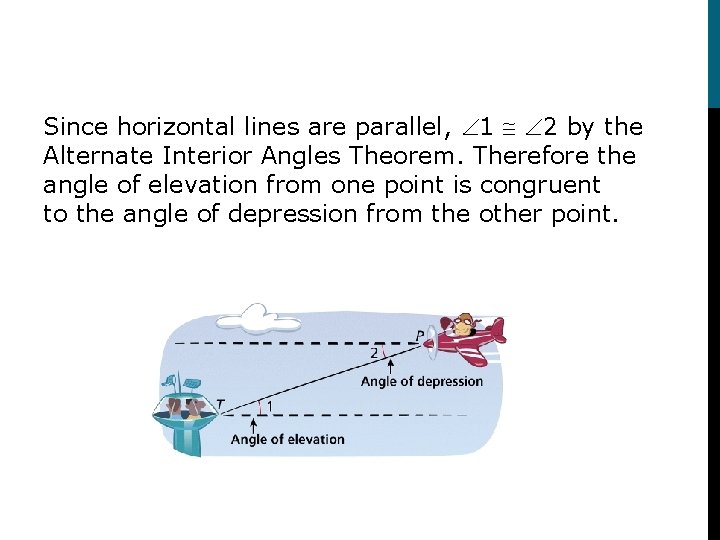
Since horizontal lines are parallel, 1 2 by the Alternate Interior Angles Theorem. Therefore the angle of elevation from one point is congruent to the angle of depression from the other point.

The sun hits the top of a tree which creates a shadow 15 feet long. If the angle of elevation from the ground to the top of the tree is 42º, how tall is the tree? x x= 15 tan 42 42º x= 13. 51 ft 15

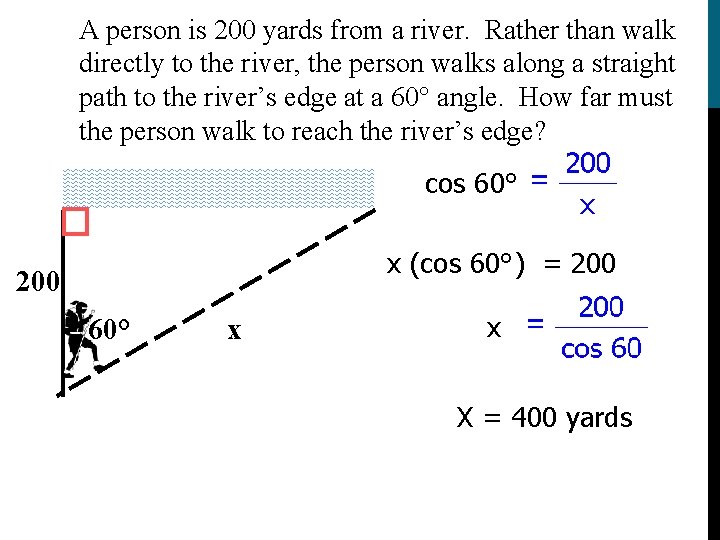
A person is 200 yards from a river. Rather than walk directly to the river, the person walks along a straight path to the river’s edge at a 60° angle. How far must the person walk to reach the river’s edge? cos 60° x (cos 60°) = 200 60° x x X = 400 yards

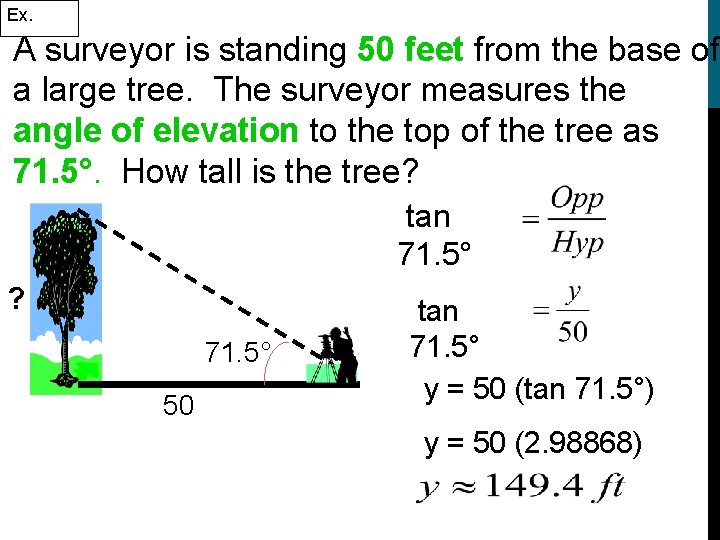
Ex. A surveyor is standing 50 feet from the base of a large tree. The surveyor measures the angle of elevation to the top of the tree as 71. 5°. How tall is the tree? tan 71. 5° ? 71. 5° 50 tan 71. 5° y = 50 (tan 71. 5°) y = 50 (2. 98868)

HAPPY LANDING A plane is flying at an altitude of 1. 5 km. The pilot wants to descend into an airport so that the path of the plane makes an angle of 5° with the ground. How far from the airport (horizontal distance) should the descent begin? 1. 5 km 5° x

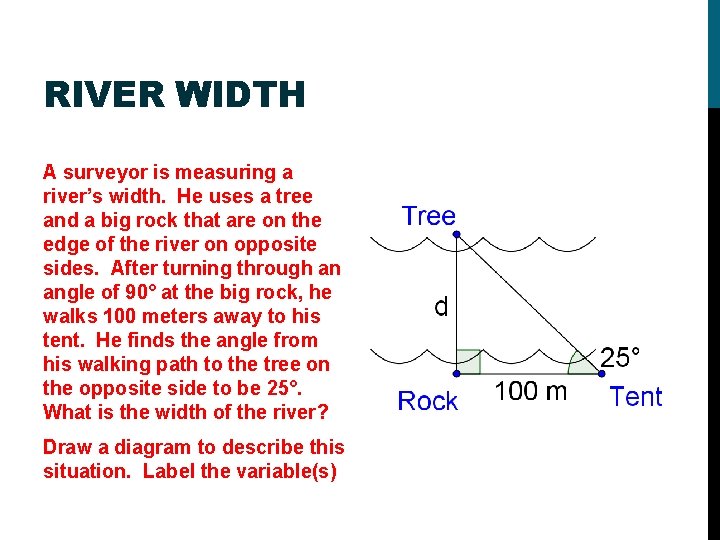
RIVER WIDTH A surveyor is measuring a river’s width. He uses a tree and a big rock that are on the edge of the river on opposite sides. After turning through an angle of 90° at the big rock, he walks 100 meters away to his tent. He finds the angle from his walking path to the tree on the opposite side to be 25°. What is the width of the river? Draw a diagram to describe this situation. Label the variable(s)

RIVER WIDTH We are looking at the “opposite” and the “adjacent” from the given angle, so we will use tangent Multiply by 100 on both sides

BUILDING HEIGHT A spire sits on top of the top floor of a building. From a point 500 ft. from the base of a building, the angle of elevation to the top floor of the building is 35 o. The angle of elevation to the top of the spire is 38 o. How tall is the spire? Construct the required triangles and label. 38 o 35 o 500 ft.

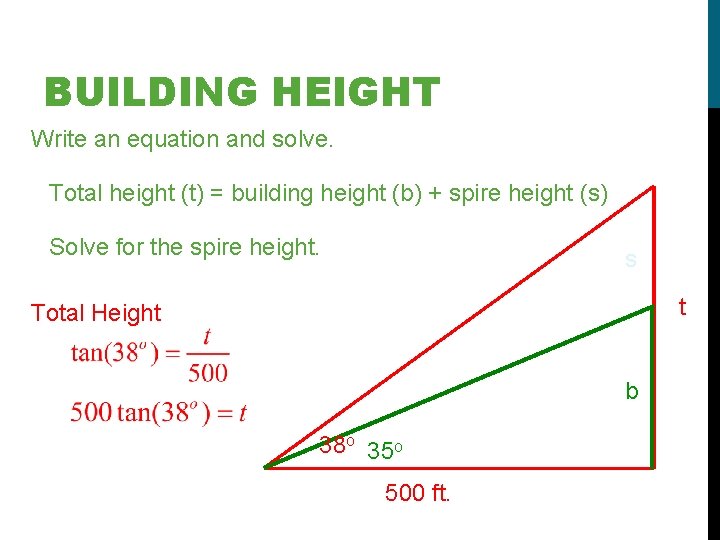
BUILDING HEIGHT Write an equation and solve. Total height (t) = building height (b) + spire height (s) Solve for the spire height. s t Total Height b 38 o 35 o 500 ft.

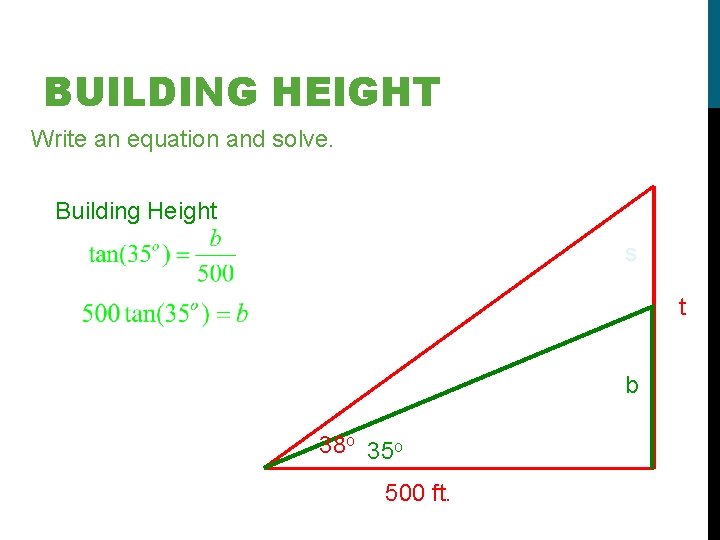
BUILDING HEIGHT Write an equation and solve. Building Height s t b 38 o 35 o 500 ft.

BUILDING HEIGHT Write an equation and solve. Total height (t) = building height (b) + spire height (s) s t The height of the spire is approximately 41 feet. b 38 o 35 o 500 ft.