TRIGONOMETR IC FUNCTIONS Trigonometric Functions of Acute Angles

TRIGONOMETR IC FUNCTIONS

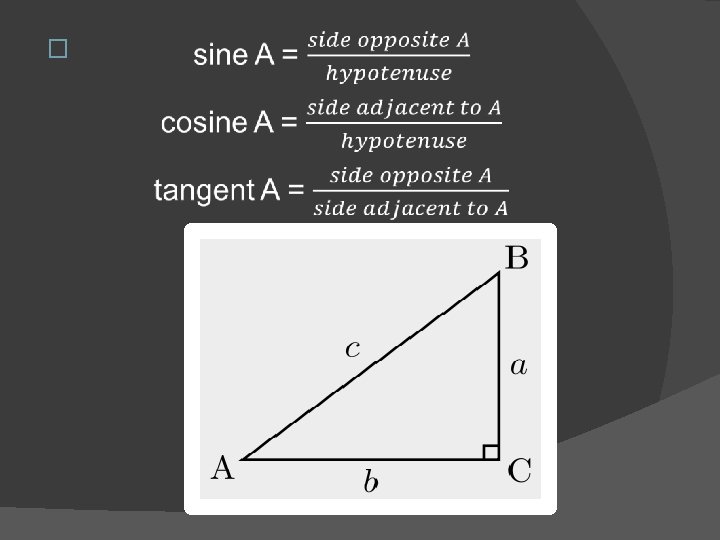
Trigonometric Functions of Acute Angles � Let us consider the right triangle ABC, with right angle at C. Angles A and B are acute angles which are complementary (A + B = 90°). The sides opposite angles A, B, and C will be denoted by the corresponding small letters a, b, and c, respectively. Then by taking ratios of the sides of the triangle, we define three trigonometric functions of acute angle A as follows:

You can use mnemonics! �

You can use mnemonics! �

Pythagorean Theorem �

Examples �

Exercises �

Do Worksheet 3

Trigonometric Functions of Any Angle θ � The trigonometric functions, which we are now ready to define, are illustrations of functions whose domains are sets of angles. � Using the Cartesian Coordinate System, we will define the six trigonometric ratios. � Let θ be an angle in standard position. Choose any point P(x, y) on the terminal side of θ. Draw a perpendicular line from P to the x-axis, thus forming a right triangle of reference for θ.

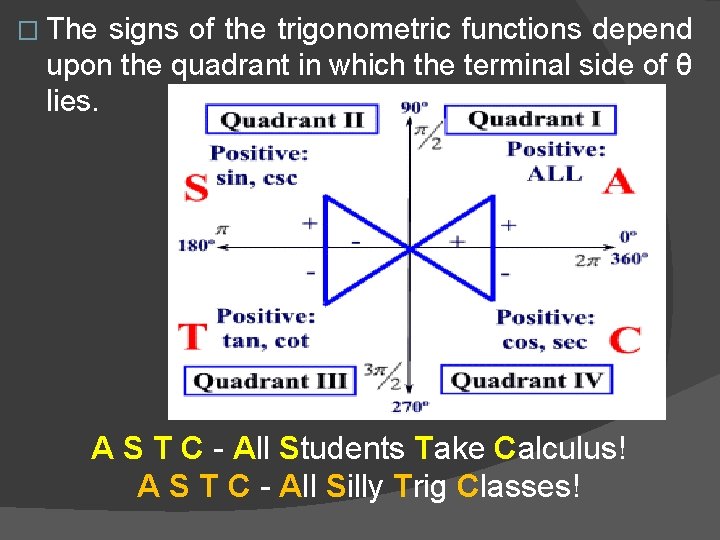
Signs of the Six Trigonometric Functions Note: r is always positive. Thus, the signs of the values of the trigonometric functions of angle θ are determined by the signs of x and y.

� The signs of the trigonometric functions depend upon the quadrant in which the terminal side of θ lies. A S T C - All Students Take Calculus! A S T C - All Silly Trig Classes!

Examples �

Reference Angle �

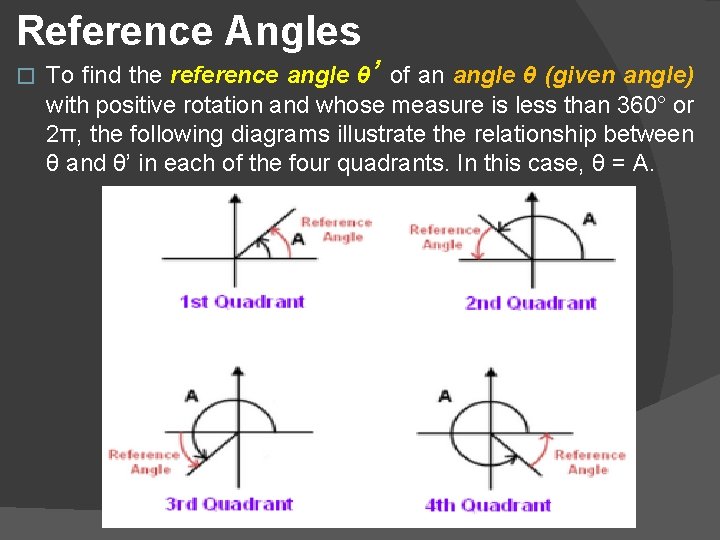
Reference Angles � To find the reference angle θ’ of an angle θ (given angle) with positive rotation and whose measure is less than 360° or 2π, the following diagrams illustrate the relationship between θ and θ’ in each of the four quadrants. In this case, θ = A.

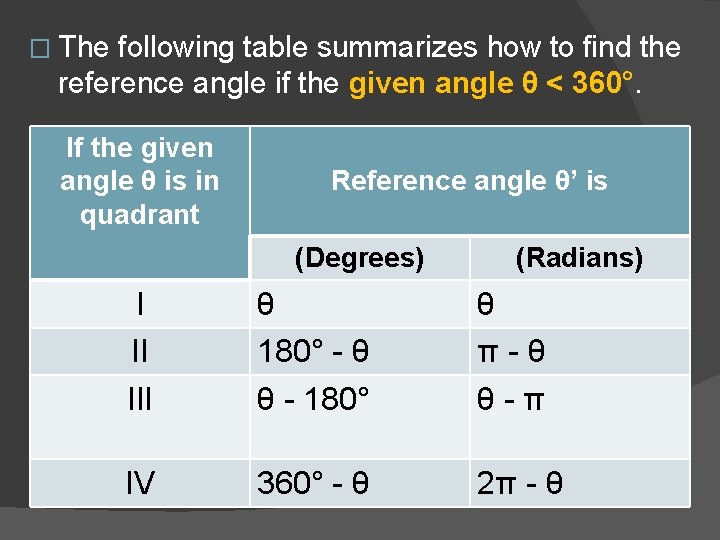
� The following table summarizes how to find the reference angle if the given angle θ < 360°. If the given angle θ is in quadrant Reference angle θ’ is (Degrees) (Radians) I II III θ 180° - θ θ - 180° θ π - θ θ - π IV 360° - θ 2π - θ

� To find the reference angle for an angle with negative measures or for an angle greater than 360°, first find a coterminal angle whose measure is between 0° and 360°. Then, use the appropriate formula summarized in the given table.

Examples Given θ is an angle in standard position. Find the measure of its reference angles θ’. 1. 250° 2. 330° 3. 125° 45’

Exercises �

Do Worksheet 4