Chapter 1 Limits and Their Properties 1 2

Chapter 1 Limits and Their Properties 1 -2 Finding Limits Graphically and Numerically • 1 -3 Evaluating Limits Analytically • 1 -4 Continuity and One-Sided Limits • 1 -5 infinite Limits • This will test the “Limits” of your brain!

1. 3 Evaluating Limits Analytically • Properties of Limits • Techniques for Evaluating Limits – Direct Substitution – Factoring and Cancelling – Rationalizing – Algebraic Manipulation • Trigonometric Rules • The Sandwich Theorem

Properties of Limits

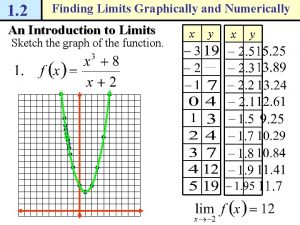
Thm. 1. 1 Some Basic Limits Examples: Think of it graphically… Let As x approaches 3, f(x) approaches 4 As x approaches 2, f(x) approaches 2 Let (y scale was adjusted to fit) As x approaches 5, f(x) approaches 125 Let b and c be real numbers and let n be a positive integer.

Thm. 1. 2 Properties of Limits: Let b and c be real numbers, let n be a positive integer, and let f and g be functions whose limits exist: üScalar Multiplication – limx c b f(x) = b limx cf(x) Ex: limx 2 3 x = 3 limx 2 x = 3 2 = 6 üSum/Difference - limx c f(x) + g(x) = limx c f(x) + limx c g(x) Ex: limx 4 x 2 + x = limx 4 x 2 + limx 4 x = 16 + 4 = 20 üProduct - limx c f(x) g(x) = limx c f(x) limx c g(x) Ex: limx πx 2 cos x =(limx π x 2)(limx π cos x)= π2 -1= -π2

Thm. 1. 2 Properties of Limits: cont… Let b and c be real numbers, let n be a positive integer, and let f and g be functions whose limits exist: üQuotient – Ex: üPowers: limx c(f(x))b = (limx cf(x))b Ex: limx 3 (4 x)2 = (limx 3 4 x)2 = (4 3)2 = 144

You Try… Given: limx c f(x) = 3 and limx c g(x) = -5 evaluate the following. 1. limx c 4 f(x) = 3. limx c [g(x)]3 = 2. limx c f(x)+g(x) = 12 4. limx c f(x) g(x) = -125 5. limx c f(x)/g(x) = -2 -15 -3/5 Note: You can only drop limx c after you substitute in the value of c.

Thm. 1. 3 Polynomial and Rational Functions • If p is a polynomial function and c is a real number, then • Also if r is a rational function such that c is a real number, such that , then Example: However, and

You Try… Evaluate each limit. You may use a calculator to verify your answer. = 30 = 7/6 If the denominator had been 0, we would NOT have been able to use direct substitution. =0 =5

Theorem 1. 4 Limits Involving a Radical Ø When evaluating limits involving radicals, remember we CANNOT take a square root, fourth root, or any other even root of negative numbers. Ø However, we CAN take a cube root, fifth root, or any other odd root of negative numbers. Ex: Evaluate each limit. DNE

Theorem 1. 5 Limit of a Composite Function If f and g are functions such that lim g(x) = L and lim f (x) = f (L), then Ex: Given find

You Try… Determine the value of each of the following. = -2 DNE =3 = -2 DNE 6. Given 7. Given , find = 64. . =7

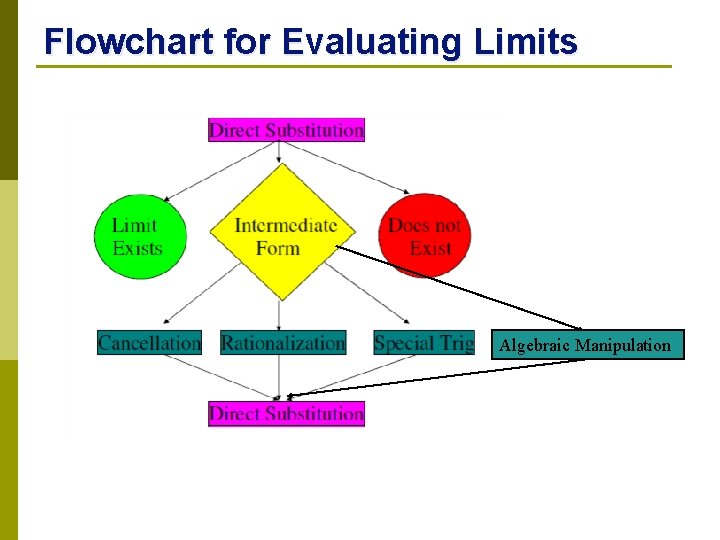
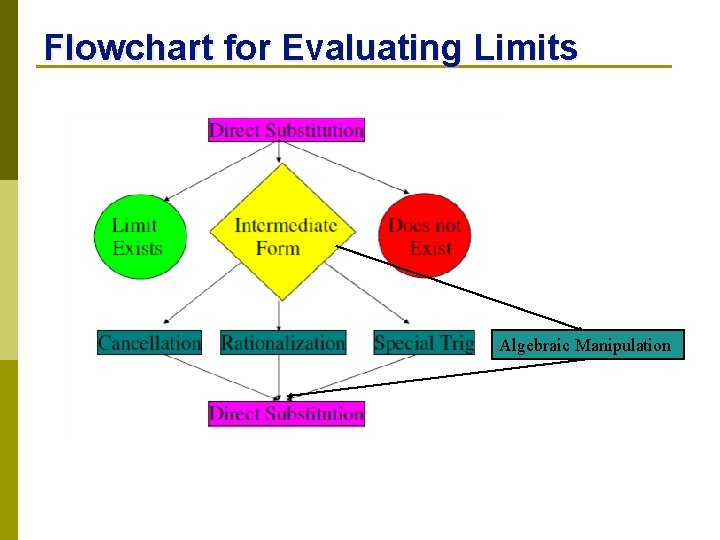
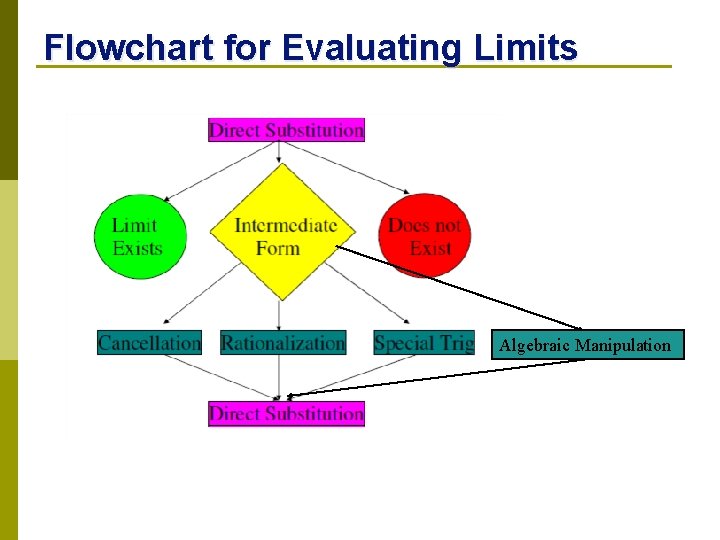
Flowchart for Evaluating Limits Algebraic Manipulation

Direct Substitution Ø When evaluating limits algebraically, the first step is to plug the value of c directly into the function. n n n Ø If you get a finite value, that is your answer. If you get 0/0, you will have to try something else. If you get a #/0, the limit is one of the infinities or DNE. Ex:

Piecewise functions Recall: lim x c f(x) = lim x c- f(x) = L for the limit to exist at x = c. + • If each branch is continuous (no jumps, holes, VA), a limit will exist at every point on each branch. The only issue you will need to check is the value where the branches meet. Compute 1. lim x 4 f(x) = 2 2. lim x -2 f(x) = 4 3. lim x 0 f(x) = 0 4. f(0) = 0

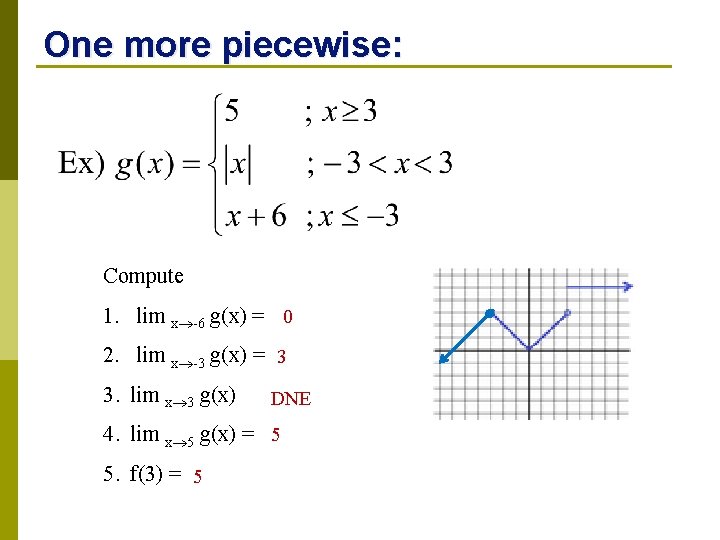
One more piecewise: Compute 1. lim x -6 g(x) = 0 2. lim x -3 g(x) = 3 3. lim x 3 g(x) DNE 4. lim x 5 g(x) = 5 5. f(3) = 5

You Try… Evaluate each of the following. 1. lim x -2 g(x) = 2 5. lim x π/2 h(x) = 1 2. lim x -5 g(x) = 0 6. lim x -2 h(x) = 2 3. lim x -3 g(x) = DNE 7. lim x 0 h(x) = 4. g(-3) = 2 8. h(0) = 0 0

You Try… Determine the value of c so that the limit exists.

Closure Explain what to do first when evaluating limits and explain the three cases that could occur.

1. 3 Evaluating Limits Analytically • Properties of Limits • Techniques for Evaluating Limits – Direct Substitution – Factoring and Cancelling – Rationalizing – Algebraic Manipulation • Trigonometric Rules • The Sandwich Theorem

Review First… A rational function is a function that can be expressed in the form where both f(x) and g(x) are polynomial functions and q(x) 0. Examples of rational functions would be:

First let’s look at This function has one value of x that is banned from the domain. Why? x 1. 5 -2 1. 9 -10 1. 99 -100 1. 999 -1000 2. 0 undefined Fill in the values in the table to see what is happening to the y-values as the x-values get closer and closer to 2 from the left side.

x 1. 5 -2 1. 9 -10 1. 99 -100 1. 999 -1000 2. 0 Und 2. 001 1000 2. 01 100 2. 1 10 2. 5 2 What about the behavior of the function on the other side of x = 2? As we pick values of x that are larger than 2 but closer and closer to 2 what do you notice is happening to values of y?

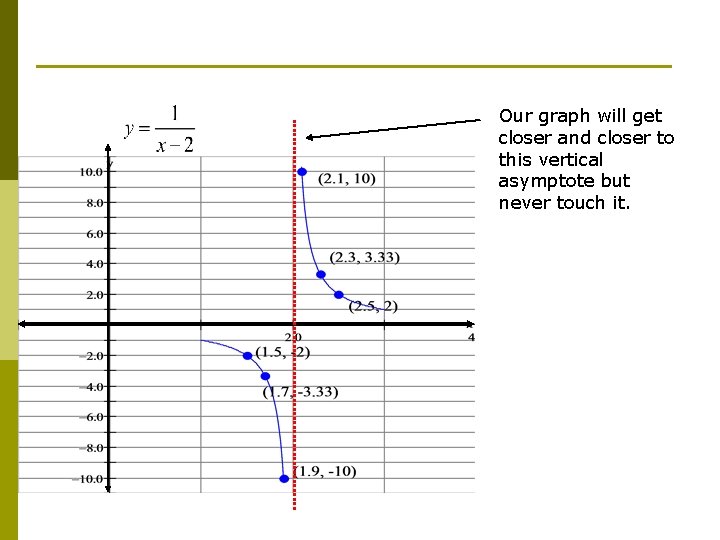
Our graph will get closer and closer to this vertical asymptote but never touch it.

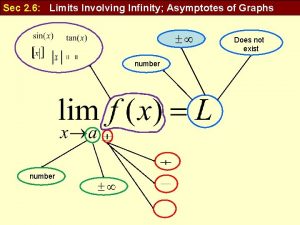
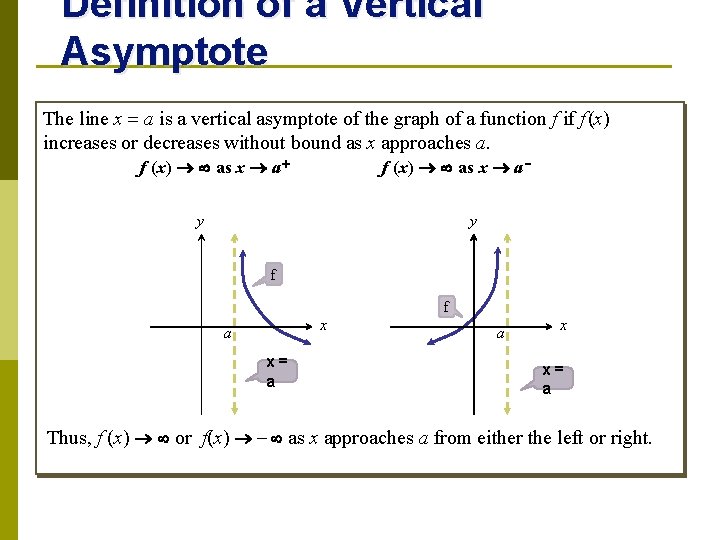
Definition of a Vertical Asymptote The line x = a is a vertical asymptote of the graph of a function f if f (x) increases or decreases without bound as x approaches a. f (x) as x a + f (x) as x a y y f x a x= a f a x x= a Thus, f (x) or f(x) - as x approaches a from either the left or right.

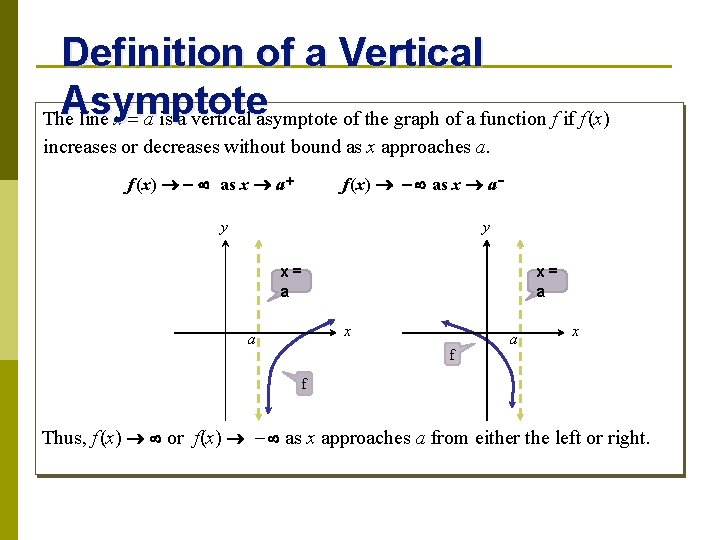
Definition of a Vertical Asymptote The line x = a is a vertical asymptote of the graph of a function f if f (x) increases or decreases without bound as x approaches a. f (x) as x a + f (x) as x a y y x= a x a f a x f Thus, f (x) or f(x) - as x approaches a from either the left or right.

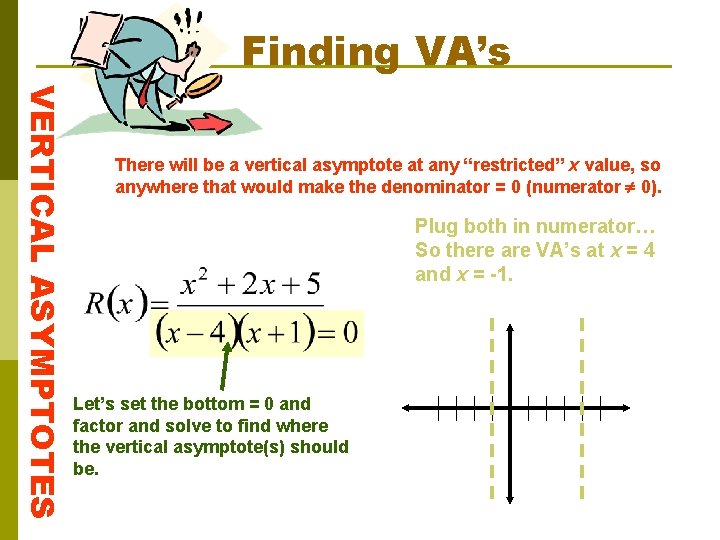
Finding VA’s VERTICAL ASYMPTOTES There will be a vertical asymptote at any “restricted” x value, so anywhere that would make the denominator = 0 (numerator 0). Plug both in numerator… So there are VA’s at x = 4 and x = -1. Let’s set the bottom = 0 and factor and solve to find where the vertical asymptote(s) should be.

HOLLA Find the vertical asymptotes: V. A. : x = 2 V. A. : x = -2, 2 V. A. : x = 0, V. A. : none 4

Now let’s look at the rational function . Determine the vertical asymptotes. It appears that we may have vertical asymptotes at x = 0 and at x = 2. We will see if a table confirms this hypothesis.

See anything peculiar? x -2 0 -1 -1 -. 5 -3 -. 1 -19 0 Und 1 3 1. 5 2. 33 1. 9 2. 05 2 und Notice that as x values get closer and closer to 0, the y values get larger and larger. This is appropriate behavior near an asymptote. But as x values get closer and closer to 2, the y values do not get large. In fact, the y values seem to get closer and closer to 2. Now, if x = 2 creates 0 in the denominator why don’t we have a VA at x = 2?

We don’t get a vertical asymptote at x = 2 because when x = 2 both the numerator and the denominator are equal to 0. In fact, if we would have reduced the function in the beginning, we could have saved ourselves a lot of trouble. Check this out: Does this mean that and are identical functions? Yes, at every value of x except x = 2 where the former is undefined. There will be a tiny hole in the graph where x = 2.

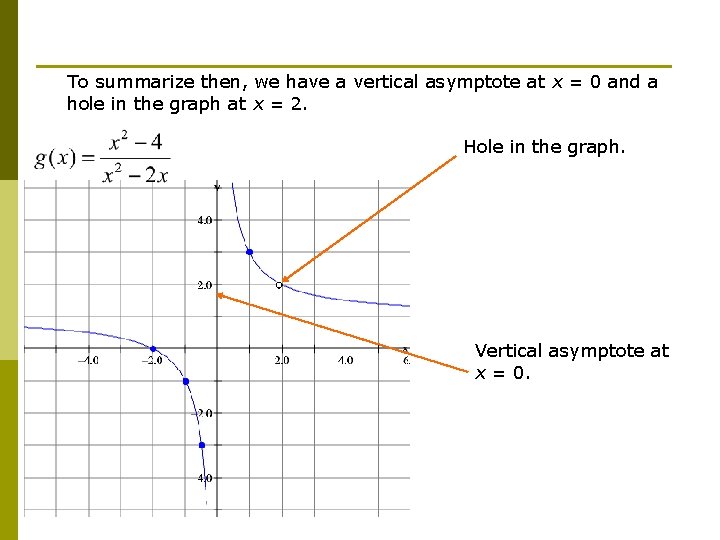
To summarize then, we have a vertical asymptote at x = 0 and a hole in the graph at x = 2. Hole in the graph. Vertical asymptote at x = 0.

Holes (Removable Discontinuities) Ø Ø If x – b is a factor of both the numerator and denominator of a rational function, then there is a hole in the graph of the function where x = b. The exact point of the hole can be found by plugging b into the function after it has been simplified. The hole is known as a removable singularity or a removable discontinuity. When you graph the function on your calculator you won’t be able to see the hole but the function is still discontinuous (has a break or jump).

Example 3 Determine the domain and any points of discontinuity and identify the type. Graph the function to confirm. Ø Ø Factor and cancel the common factors. Set the canceled factor = 0 and solve. Plug the value back into the factored form to find the hole. The factor that is left helps you find the VA.

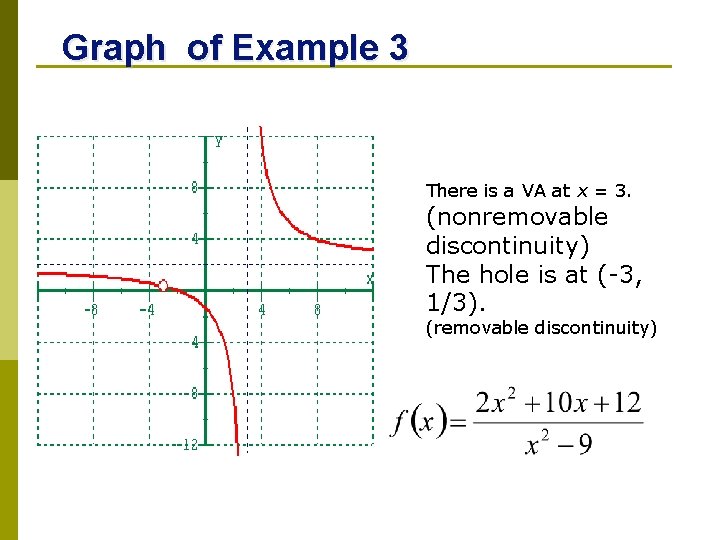
Graph of Example 3 There is a VA at x = 3. (nonremovable discontinuity) The hole is at (-3, 1/3). (removable discontinuity)

Example 4 Determine the domain and any points of discontinuity and identify the type. Graph the function to confirm. Ø Factor both numerator and denominator to see if there any common factors. Ø Because there is a common factor of x - 2 there will be a hole at x = 2. Plug x = 2 into the factored form to find the y-value of the hole y = 3. Ø Since (x + 2) is still in the denominator, there is a VA at x = -2.

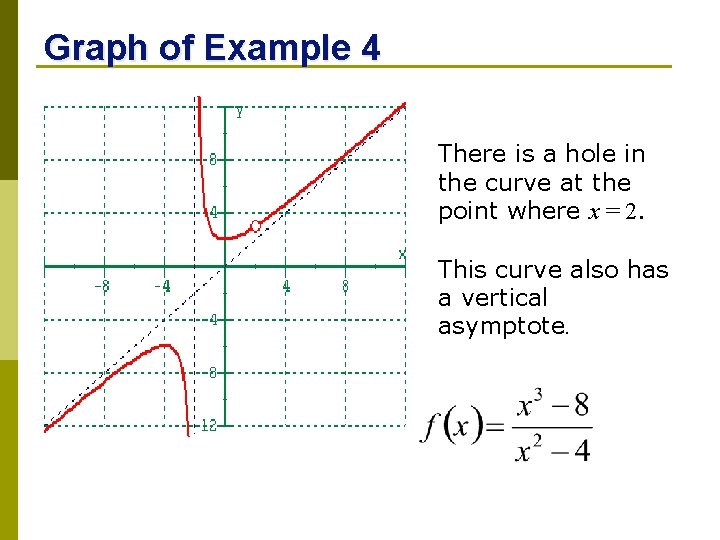
Graph of Example 4 There is a hole in the curve at the point where x = 2. This curve also has a vertical asymptote.

You Try… Identify any vertical asymptotes & holes. Graph to confirm.

You Try… Identify any vertical asymptotes & holes. Graph to confirm.

You Try… Identify any vertical asymptotes & holes. Graph to confirm.

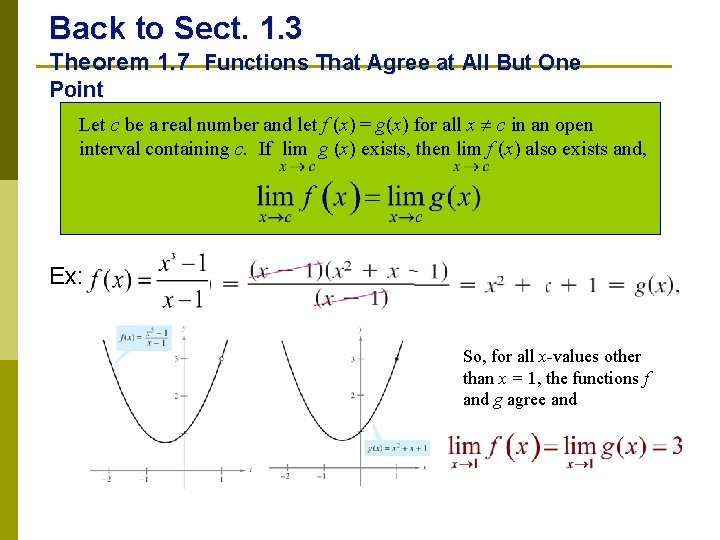
Back to Sect. 1. 3 Theorem 1. 7 Functions That Agree at All But One Point Let c be a real number and let f (x) = g(x) for all x c in an open interval containing c. If lim g (x) exists, then lim f (x) also exists and, Ex: So, for all x-values other than x = 1, the functions f and g agree and

Flowchart for Evaluating Limits Algebraic Manipulation

Factoring and Cancelling Note: Expressions such as since are called indeterminate form the limit cannot be determined. Technique - factor, cancel, and then try direct substitution one more time.

You Try… 1. Evaluate 2. Evaluate

Rationalizing Evaluate Using direct substitution we get: Technique - multiply by the conjugate to eliminate radicals.

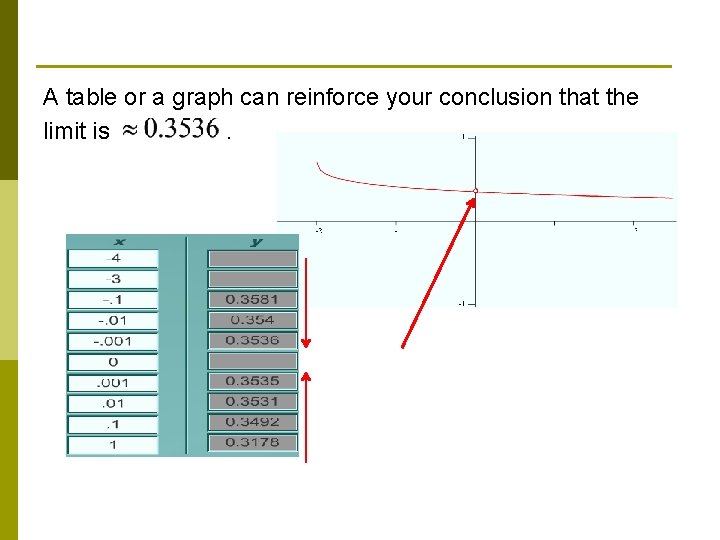
A table or a graph can reinforce your conclusion that the limit is.

You Try… 1. Evaluate 2. Evaluate

Algebraic Manipulation Using direct substitution we get: Technique – get a common denominator and simplify.

You Try…

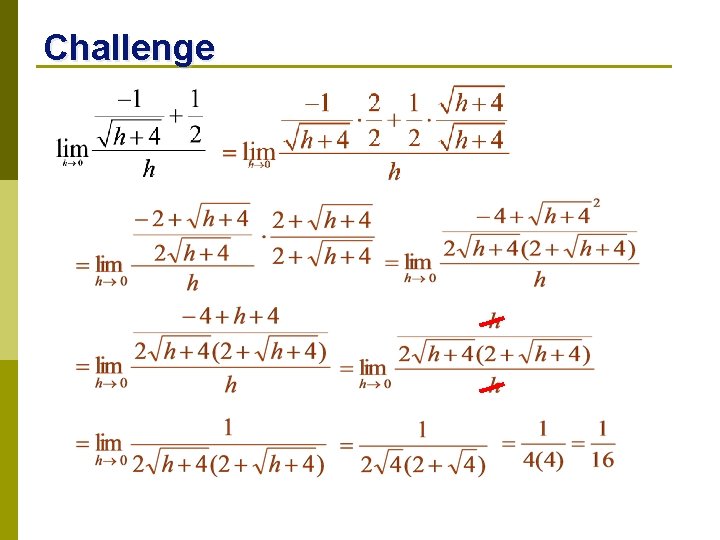
Challenge

Practice Evaluate each of the following by hand. You may use a calculator to check your answer.

Closure What is meant by an indeterminate form? Give an example where an indeterminate form gives different answers.

1. 3 Evaluating Limits Analytically • Properties of Limits • Techniques for Evaluating Limits – Direct Substitution – Factoring and Cancelling – Rationalizing – Algebraic Manipulation • Trigonometric Rules • The Sandwich Theorem

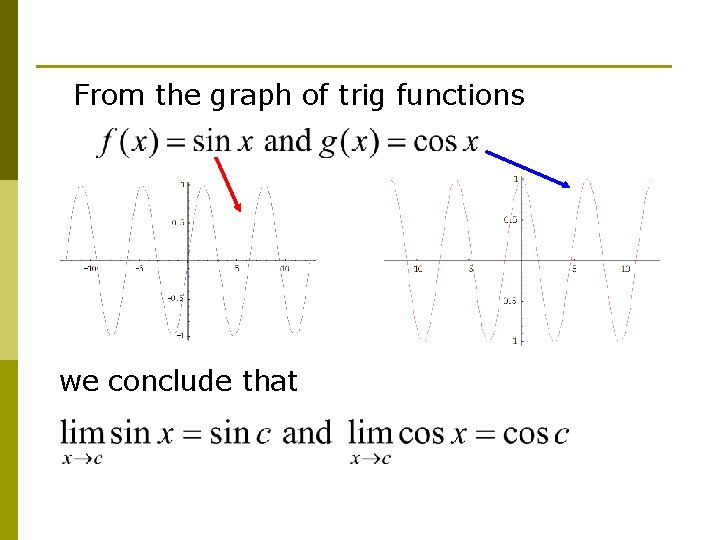
From the graph of trig functions we conclude that

Tangent and secant, however, have a restricted domain.

Theorem 1. 6 Limits of Trig Functions Let c be a real number in the domain of the given trigonometric function 1. 2. 3. 4. 5. 6.

Limits of Trig Functions Examples: 1. 2. 3.

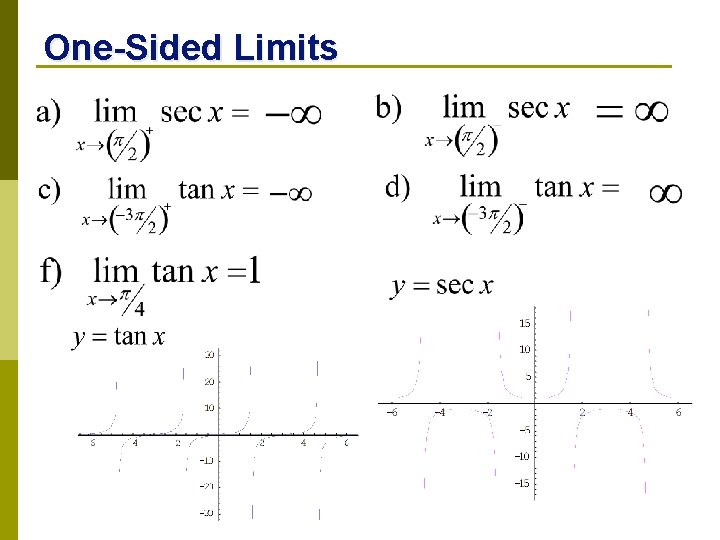
One-Sided Limits

Flowchart for Evaluating Limits Algebraic Manipulation

Special Trig Limits Here are two rules you will want to memorize: 1. Rule 1: 2. Rule 2: OR OR http: //www. youtube. com/watch? v=j. QDIo. XDl. Hd. A (proof of Rule 1 – also in book)

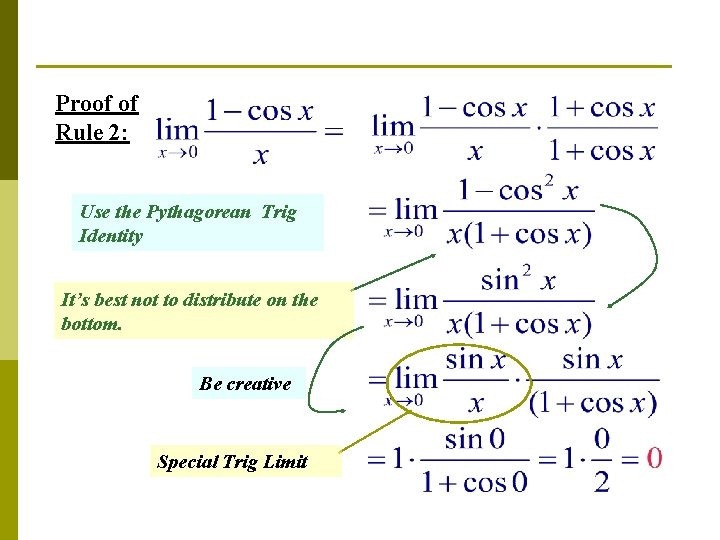
Proof of Rule 2: Use the Pythagorean Trig Identity It’s best not to distribute on the bottom. Be creative Special Trig Limit

Limits of Trig Functions Evaluate =1 Using direct substitution we get: Technique – use a special trig limit and algebraic manipulation if necessary. This 5 is a constant and can be pulled out in front of the limit. You will need the bottom to also be 5 x in order to use Rule 1. Multiply the top and bottom by 5.

Evaluate =1 Direct substitution won’t work. We can use the sine trig limit, but first we’ll have to use some algebra since we need the bottom to be a 3 x. Evaluate Direct substitution works at this point since the bottom of the fraction will not be 0 when you use π/2.

You Try… Calculate each of the following limits. 1. 2. 3.

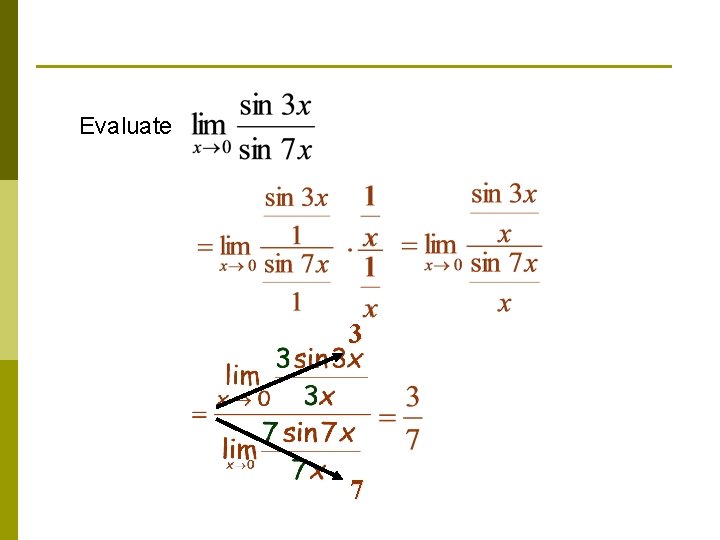
Evaluate 3 7

You Try… Calculate each of the following limits. 1. 2. 3.

Trigonometric Rules of Limits Here a few more (but are not necessary to memorize): Rule 3: OR Rule 4: OR Rule 5: OR

Example Find Solution

Find 4 4

You Try… Calculate each of the following limits. 1. 4. 2. 5. 3. 6.

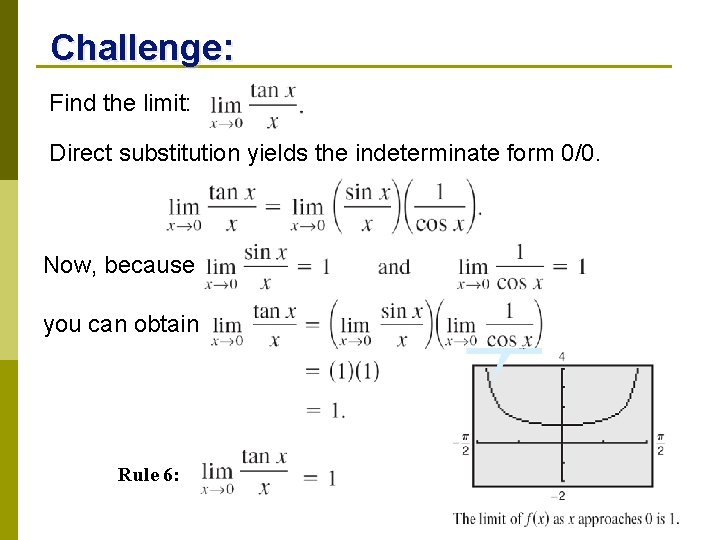
Challenge: Find the limit: Direct substitution yields the indeterminate form 0/0. Now, because you can obtain Rule 6:

You Try… Calculate each of the following limits. 1. 2. 3.

Flowchart for Evaluating Limits Algebraic Manipulation

Evaluating Limits Summary 1 st substitution get answer? ? Then you are done get ? ? Then limit is 0. get ? ? Then limit DNE (∞ or -∞). get ? ? indeterminate form Þ polynomial ? ? Try factoring and canceling. Þ radical? ? Try rationalizing (multiply by the conjugate). Þ fraction in a fraction? ? Try a common denominator and simplify. Þ trig function? ? Try a special trig limit

1. 3 Evaluating Limits Analytically • Properties of Limits • Techniques for Evaluating Limits – Direct Substitution – Factoring and Cancelling – Rationalizing – Algebraic Manipulation • Trigonometric Rules • The Sandwich Theorem

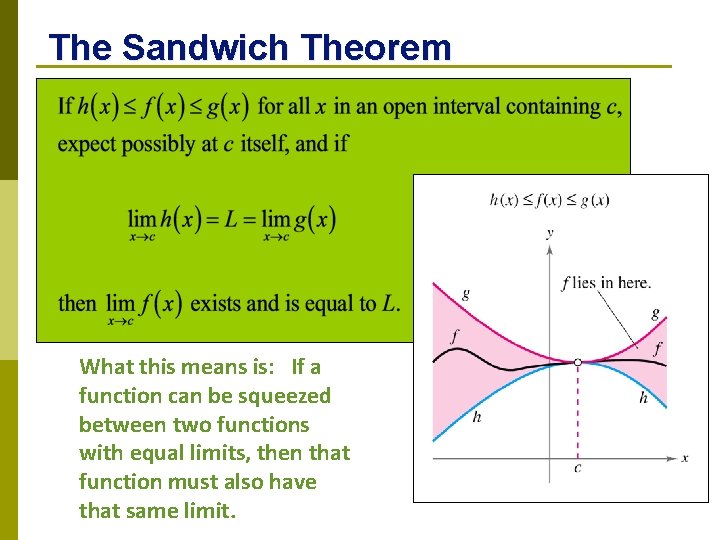
The Sandwich Theorem What this means is: If a function can be squeezed between two functions with equal limits, then that function must also have that same limit.

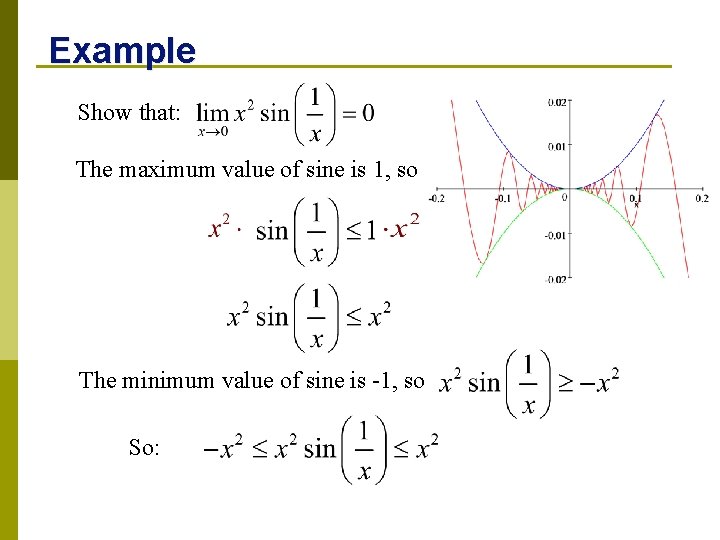
Example Show that: The maximum value of sine is 1, so The minimum value of sine is -1, so So:

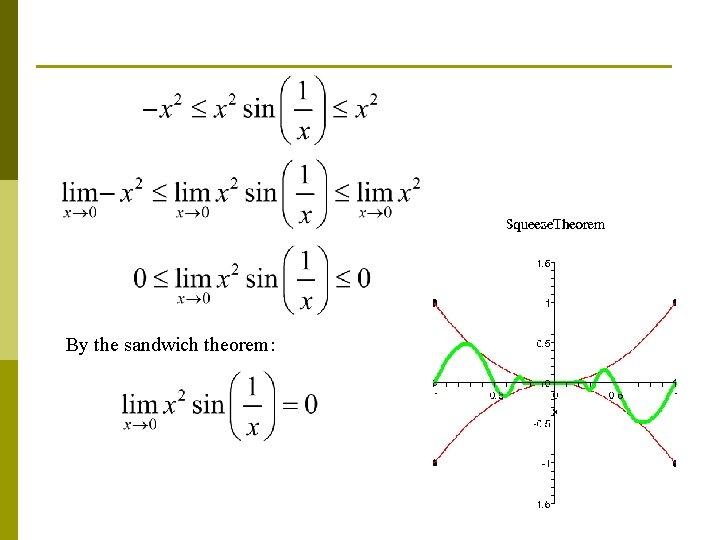
By the sandwich theorem:

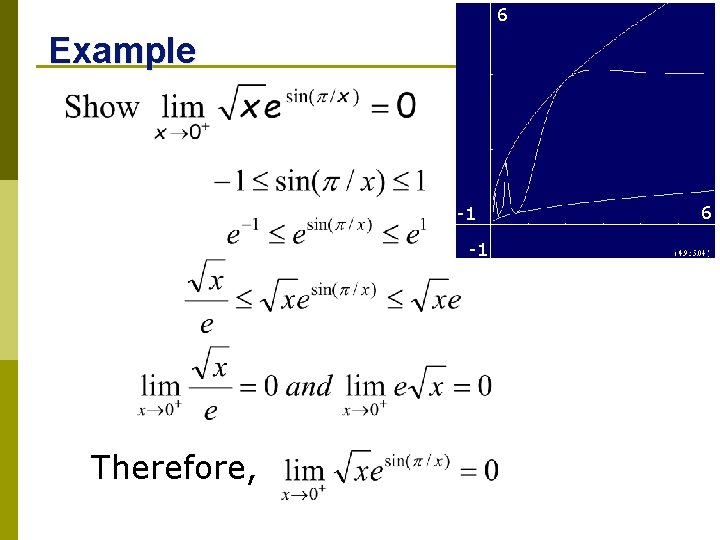
6 Example -1 -1 Therefore, 6

You Try… Ø Calculate the following limits. 1. =0 2. = 29 200 5 -5 -200

Techniques for Evaluating Limits Ø It can be a little trickier to determine limits without the benefit of looking at a graph; but with the help of a few techniques, it’s very manageable: 1. Direct substitution Ø 2. Factor and Cancel Ø 3. Get a common denominator and simplify. Trigonometric Rules Ø 6. Multiply by the conjugate to eliminate radicals Algebraic Manipulation Ø 5. Factor, cancel, then use direct substitution Rationalization Ø 4. Plug in c into the function Apply special trigonometric limits The Sandwich Theorem Ø Try to squeeze the function between two functions whose limits can be easily calculated and are equal.