Inverse Functions Inverse Relations The inverse of a


























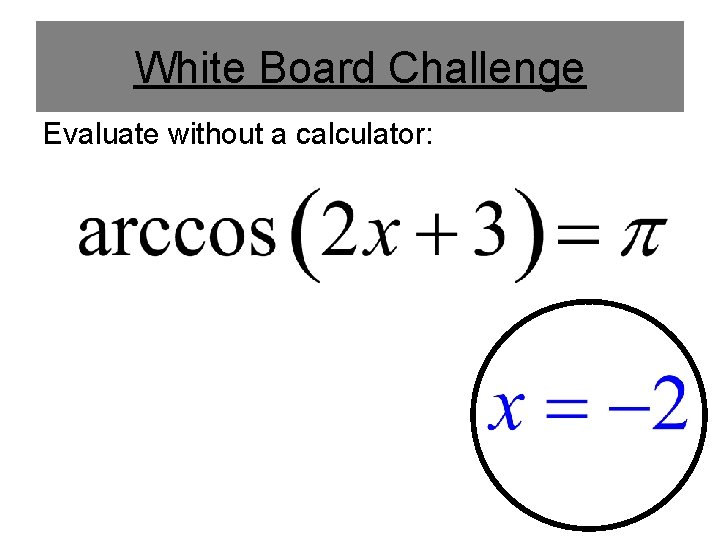

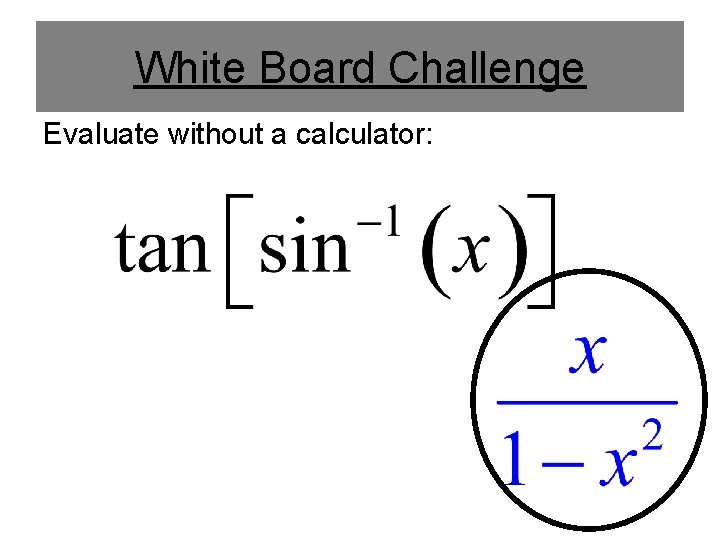
- Slides: 39

Inverse Functions

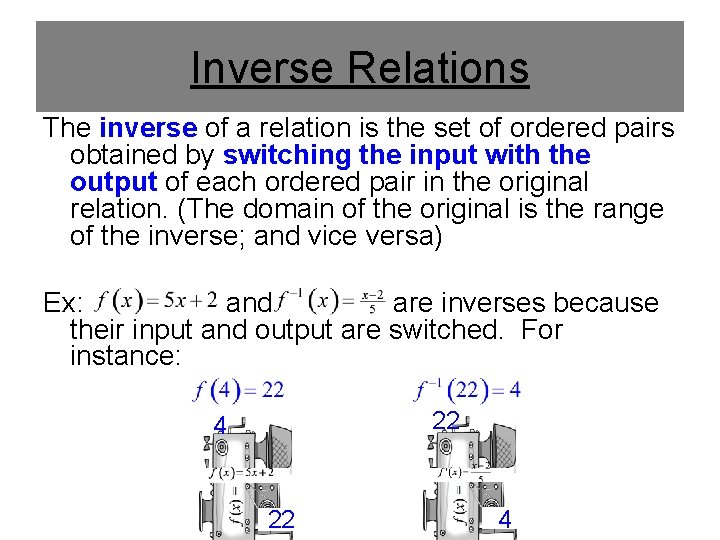
Inverse Relations The inverse of a relation is the set of ordered pairs obtained by switching the input with the output of each ordered pair in the original relation. (The domain of the original is the range of the inverse; and vice versa) Ex: and are inverses because their input and output are switched. For instance: 22 4

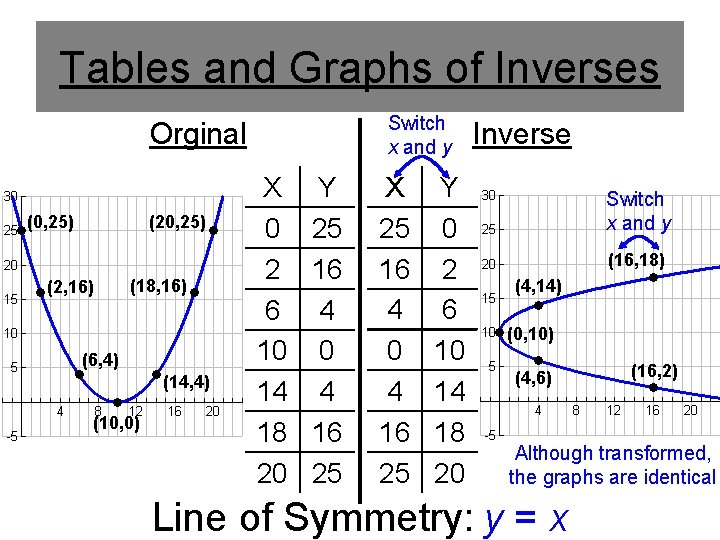
Tables and Graphs of Inverses Switch x and y Orginal (0, 25) (2, 16) (18, 16) (6, 4) (14, 4) (10, 0) X 0 2 6 10 14 18 20 Y 25 16 4 0 4 16 25 X 25 16 4 0 4 16 25 Y 0 2 6 10 14 18 20 Inverse Switch x and y (16, 18) (4, 14) (0, 10) (4, 6) (16, 2) Although transformed, the graphs are identical Line of Symmetry: y = x

Inverse and Compositions In order for two functions to be inverses: AND

One-to-One Functions A function f(x) is one-to-one on a domain D if, for every value c, the equation f(x) = c has at most one solution for every x in D. Or, for every a and b in D: Theorems: 1. A function has an inverse function if and only if it is one-to-one. 2. If f is strictly monotonic (strictly increasing or decreasing) on its entire domain, then it is one-to-one and therefore has an inverse function.

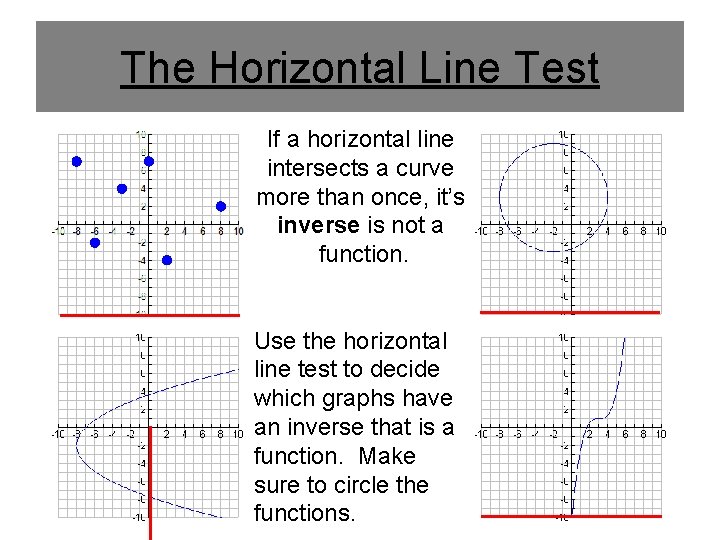
The Horizontal Line Test If a horizontal line intersects a curve more than once, it’s inverse is not a function. Use the horizontal line test to decide which graphs have an inverse that is a function. Make sure to circle the functions.

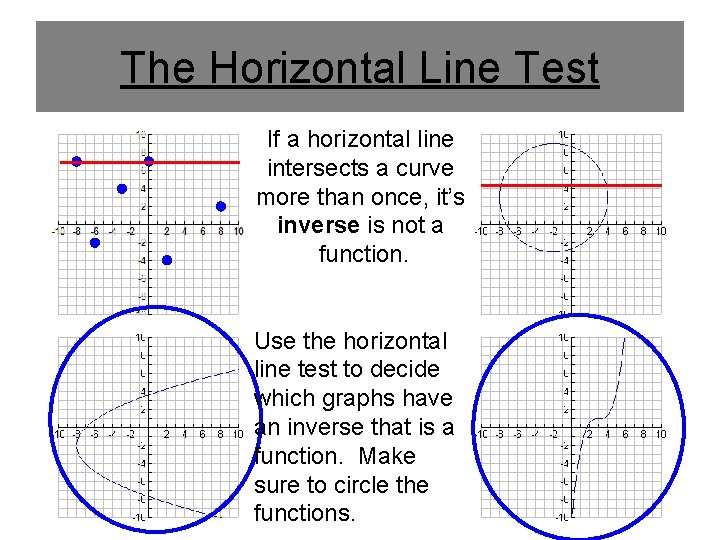
The Horizontal Line Test If a horizontal line intersects a curve more than once, it’s inverse is not a function. Use the horizontal line test to decide which graphs have an inverse that is a function. Make sure to circle the functions.

Example Without graphing, decide if the function below has an inverse function. If f is strictly monotonic (strictly increasing or decreasing) on its entire domain, then it is one-to-one and therefore has an inverse function. See if the derivative is always one sign: Since the derivative is always negative, the inverse of f is a function.

Find the Inverse of a Function 1. Switch the x and y of the function whose inverse you desire. 2. Solve for y to get the Inverse function 3. Make sure that the domains and ranges of your inverse and original function match up.

Example Find the inverse of the following: Only Half Parabola Switch x and y Really y = Solve for y Full Parabola (too much) Restrict the Domain! x=3 Make sure to check with a table and graph on the calculator.

Logarithms v Exponentials

Definition of Logarithm The logarithm base a of b is the exponent you put on a to get b: a>0 and b>0 i. e. Logs give you exponents! The logarithm to the base e, denoted ln x, is called the natural logarithm.

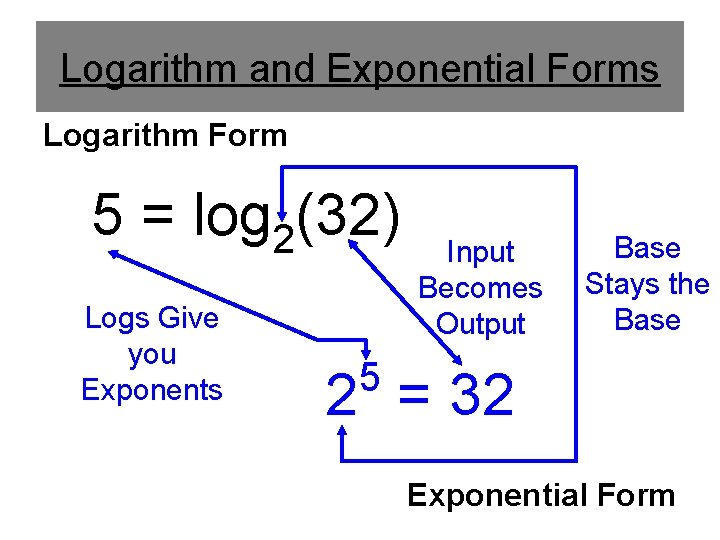
Logarithm and Exponential Forms Logarithm Form 5 = log 2(32) Logs Give you Exponents Input Becomes Output Base Stays the Base 5 2 = 32 Exponential Form

Examples Write each equation in exponential form 1. log 125(25) = 2/3 1252/3 = 25 2. Log 8(x) = 1/3 81/3 = x Write each equation in logarithmic form 1. If 64 = 4 3 2. If 1/27 = 3 x log 4(64) = 3 Log 3(1/27) = x

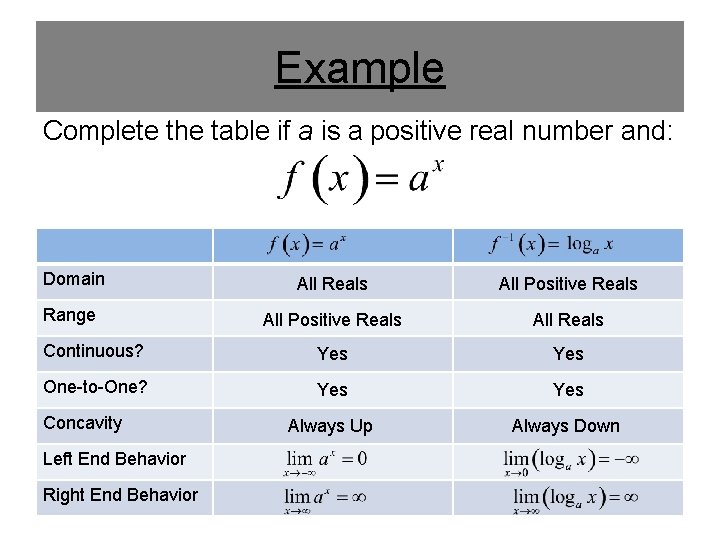
Example Complete the table if a is a positive real number and: Domain All Reals All Positive Reals Range All Positive Reals All Reals Continuous? Yes One-to-One? Yes Always Up Always Down Concavity Left End Behavior Right End Behavior

The Change of Base Formula The following formula allows you to evaluate any valid logarithm statement: For a and b greater than 0 AND b≠ 1. Example: Evaluate

Solving Equations with the Change of Base Formula Solve: Isolate the base and power Change the exponential equation to an logarithm equation Use the Change of Base Formula

Properties of Logarithms For a>0, b>0, m≠ 1, and any real number n. Logarithm of 1: Logarithm of the base: Power Property: Product Property: Quotient Property:

Example 1 Condense the expression:

Example 2 Expand the expression:

Example 3 Solve the equation:

AP Reminders Do not forget the following relationships:

Inverse Trigonometry

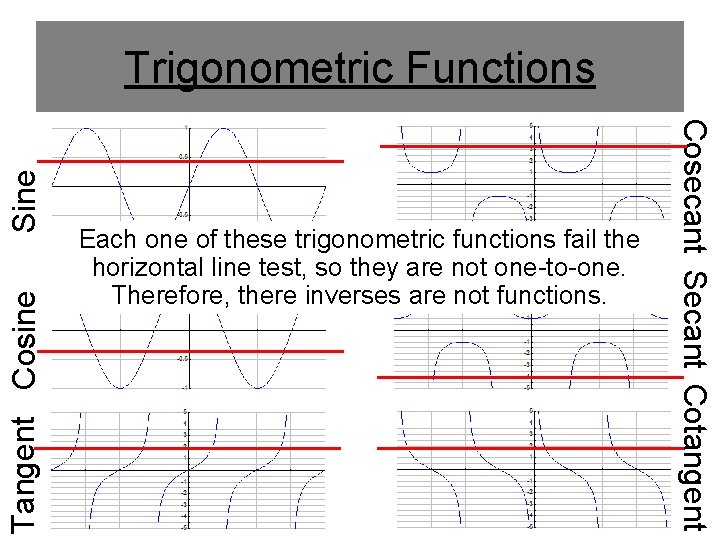
Tangent Cosine Each one of these trigonometric functions fail the horizontal line test, so they are not one-to-one. Therefore, there inverses are not functions. Cosecant Secant Cotangent Sine Trigonometric Functions

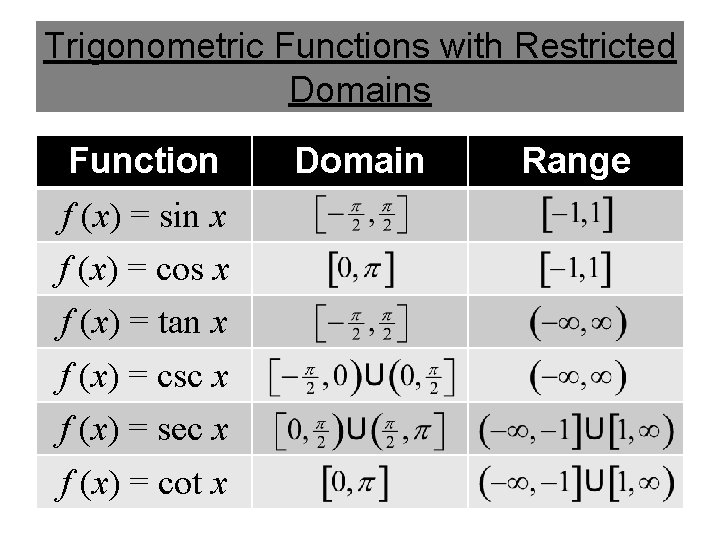
Tangent Cosine In order for their inverses to be functions, the domains of the trigonometric functions are restricted so that they become oneto-one. Cosecant Secant Cotangent Sine Trigonometric Functions with Restricted Domains

Trigonometric Functions with Restricted Domains Function f (x) = sin x f (x) = cos x f (x) = tan x f (x) = csc x f (x) = sec x f (x) = cot x Domain Range

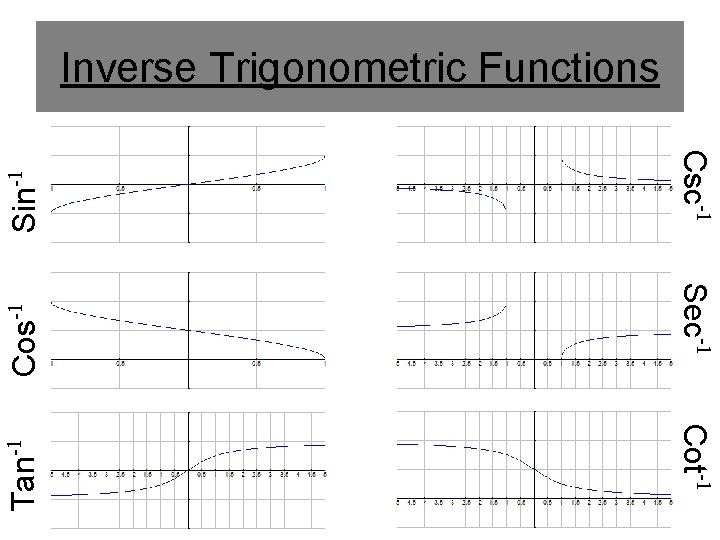
Cos-1 Sec-1 Cot-1 Tan-1 Csc-1 Sin-1 Inverse Trigonometric Functions

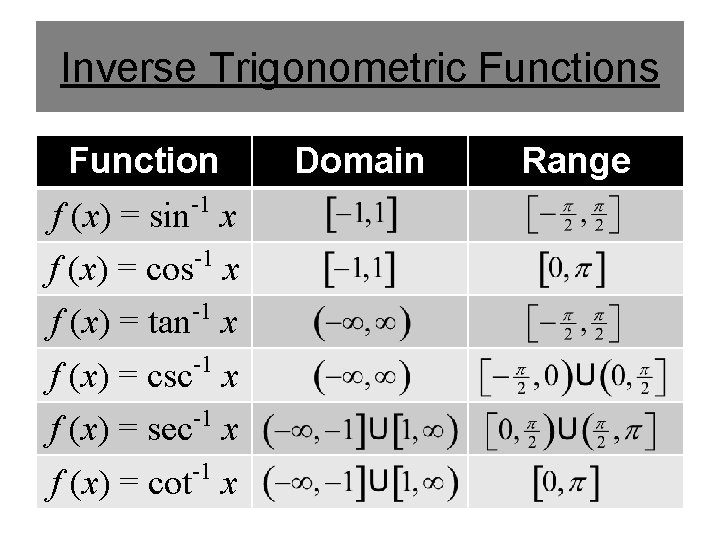
Inverse Trigonometric Functions Function f (x) = sin-1 x f (x) = cos-1 x -1 f (x) = tan x f (x) = csc-1 x -1 f (x) = sec x -1 f (x) = cot x Domain Range

Alternate Names/Defintions for Inverse Trigonometric Functions Familiar f (x) = sin-1 x -1 f (x) = cos x -1 f (x) = tan x f (x) = csc-1 x -1 f (x) = sec x -1 f (x) = cot x Alternate Calculator f (x) = arcsin x f (x) = sin-1 x -1 f (x) = arccos x f (x) = cos x -1 f (x) = arctan x f (x) = arccsc x f (x) = sin-1 1/x -1 f (x) = arcsec x f (x) = cos 1/x -1 f (x) = arccot x f (x) = -tan x+ Arccot is different because it is always positive but tan can be negative.

Example 1 Evaluate: This expression asks us to find the angle whose sine is ½. Remember the range of the inverse of sine is.

Example 2 Evaluate: This expression asks us to find the angle whose cosecant is -1 (or sine is -1). Remember the range of the inverse of cosecant is.

Example 3 Evaluate: The embedded expression asks us to find the angle whose sine is 1/3. Draw a picture (There are infinite varieties): It does not even matter what the angle is, we only need to find: Find the missing side length(s) Is the result positive or negative?

Example 4 Evaluate: The embedded expression asks us to find the angle whose cosine is -1/6. Ignore the Draw a picture (There are infinite varieties): negative for now. It does not even matter what the angle is, we only need to find: Find the missing side length(s) Is the result positive or negative?

Example 3 Evaluate: The embedded expression asks us to find the angle whose tangent is x. Draw a possible picture (There are infinite varieties): It does not even matter what the angle is, we only need to find: Find the missing side length(s) Is the result positive or negative?

White Board Challenge Evaluate without a calculator:

White Board Challenge Evaluate without a calculator:
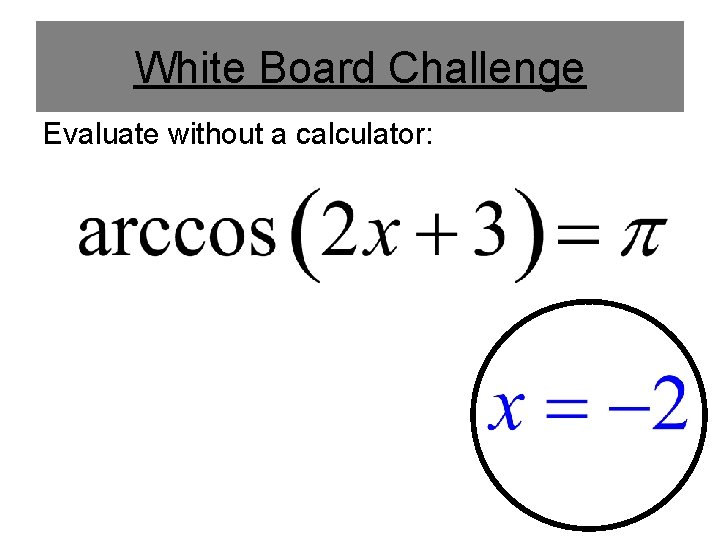
White Board Challenge Evaluate without a calculator:

White Board Challenge Evaluate without a calculator:
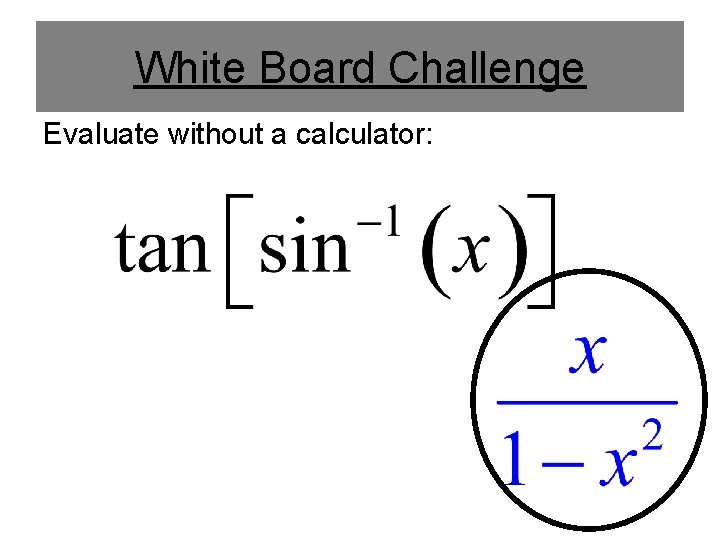
White Board Challenge Evaluate without a calculator: