INVERSE FUNCTIONS INVERSE FUNCTIONS ESSENTIAL QUESTION HOW ARE

INVERSE FUNCTIONS

INVERSE FUNCTIONS ESSENTIAL QUESTION HOW ARE THE DOMAIN AND RANGES OF INVERSES RELATED TO EACH OTHER?

Vocabulary • Inverse function – a function where the x and y values are switched from the original function • You can think of a function and its inverse as the “DO” and “UNDO” functions • A function takes a starting value, does an operation on it, and creates an output answer • An inverse starts with the output answer, does an operation on it, and arrives back at the starting value • One-to-one-function – a function whose inverse is also a function

Notation for an inverse function

Graph of an inverse function • Make an x-y table • Graph • Switch the x and y values in the table • Graph the new values • The inverse will be a reflection in the line y=x

Example • Graph the inverse of y = x 2 - 2

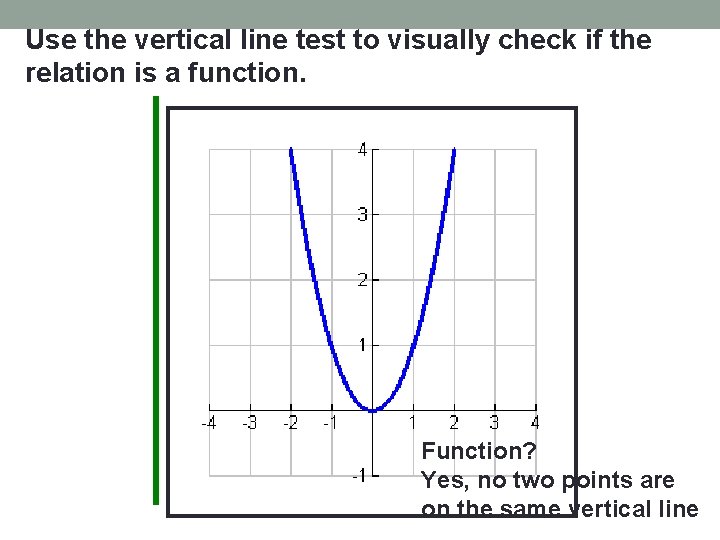
Remember the vertical line test? • Used to tell if a relation is a function • If a vertical line hits a function in only one place at a time, the relation is a function

Use the vertical line test to visually check if the relation is a function. Function? Yes, no two points are on the same vertical line

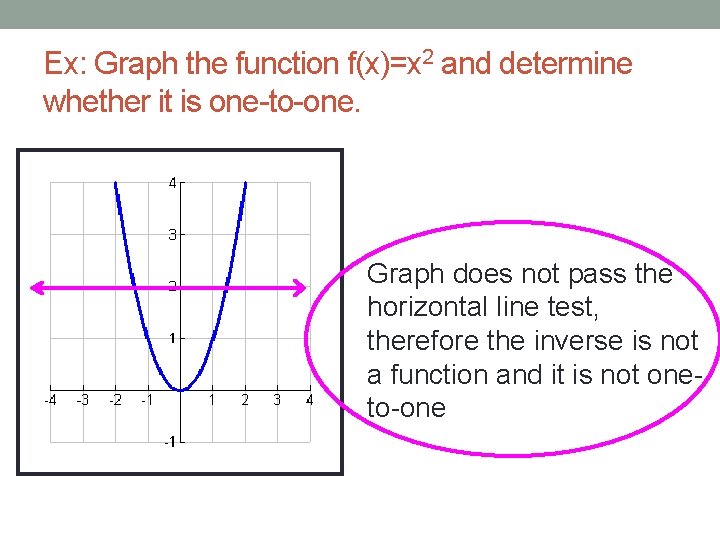
Horizontal Line Test � Used to determine whether a function’s inverse will be a function � If the original function passes the vertical line test AND the horizontal line test, then its inverse is a function � We call this ONE-TO-ONE. � If the original function does not pass the horizontal line test, then its inverse is not a function

Ex: Graph the function f(x)=x 2 and determine whether it is one-to-one. Graph does not pass the horizontal line test, therefore the inverse is not a function and it is not oneto-one

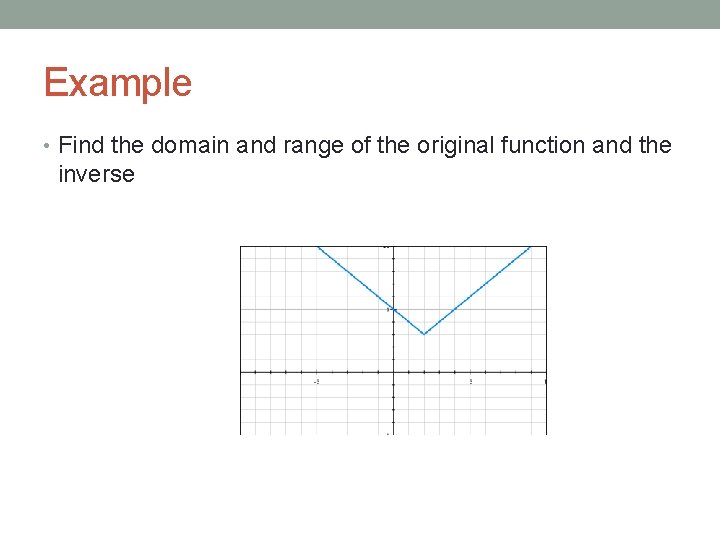
Domain and Range • Remember domain and range? ? • Domain is all the X values • Range is all the Y values • The DOMAIN of a function is the same as the RANGE of the inverse (because you switch x and y values) • The RANGE of a function is the same as the DOMAIN of the inverse

Example • Find the domain and range of the original function and the inverse