7 INVERSE FUNCTIONS INVERSE FUNCTIONS 7 3 The















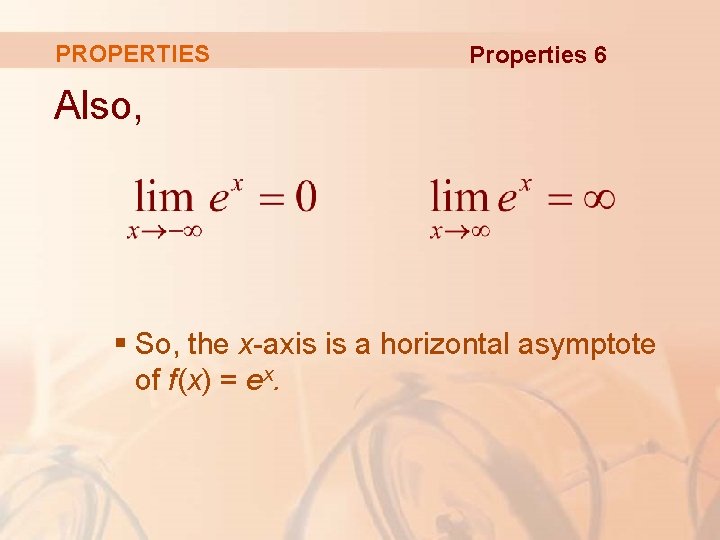
























- Slides: 47

7 INVERSE FUNCTIONS

INVERSE FUNCTIONS 7. 3* The Natural Exponential Function In this section, we will learn about: The natural exponential function and its properties.

THE NATURAL EXPONENTIAL FUNCTION Since ln is an increasing function, it is one-to-one and, therefore, has an inverse function. § We denote this by: exp

NATURAL EXP. FUNCTION Notation 1 Thus, according to the definition of an inverse function,

NATURAL EXP. FUNCTION Equations 2 The cancellation equations are: § In particular, we have: exp(0) = 1 since ln 1 = 0 exp(0) = e since ln e = 1

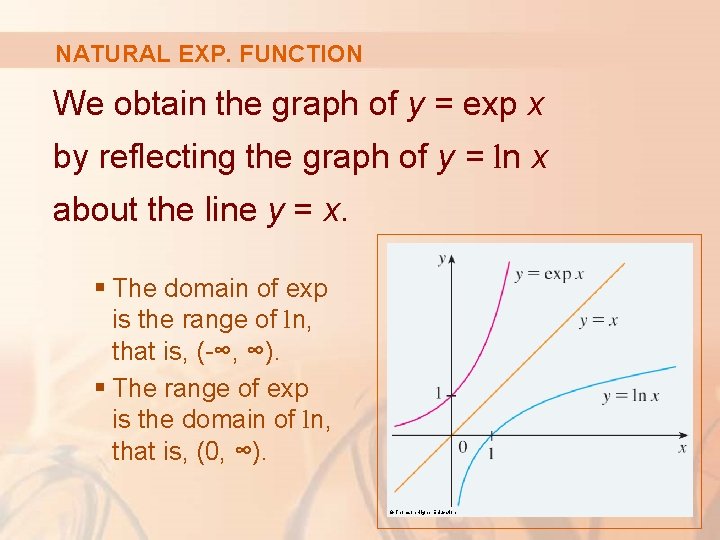
NATURAL EXP. FUNCTION We obtain the graph of y = exp x by reflecting the graph of y = ln x about the line y = x. § The domain of exp is the range of ln, that is, (-∞, ∞). § The range of exp is the domain of ln, that is, (0, ∞). © Thomson Higher Education

NATURAL EXP. FUNCTION If r is any rational number, the third law of logarithms gives: ln(er ) = r ln e = r § Therefore, by Notation 1, exp(r) = er § Thus, exp(x) = ex whenever x is a rational number.

NATURAL EXP. FUNCTION This leads us to define ex, even for irrational values of x, by the equation ex = exp(x) § In other words, for the reasons given, we define ex to be the inverse of the function ln x.

NATURAL EXP. FUNCTION Notation 3 In this equation, Notation 1 becomes:

NATURAL EXP. FUNCTION Equations 4 & 5 The cancellation Equations 2 become:

NATURAL EXP. FUNCTION E. g. 1—Solution 1 Find x if ln x = 5. § From Notation 3, we see that: ln x = 5 means § Therefore, x = e 5 = x

NATURAL EXP. FUNCTION E. g. 1—Solution 2 Start with the equation ln x = 5 § Then, apply the exponential function to both sides of the equation: e ln x = e 5 § However, Equation 4 says that: e ln x = x § Therefore, x = e 5.

NATURAL EXP. FUNCTION Example 2 Solve the equation e 5 -3 x = 10. § We take natural logarithms of both sides of the equation and use Equation 5:

NATURAL EXP. FUNCTION Example 2 § Since the natural logarithm is found on scientific calculators, we can approximate the solution to four decimal places: x ≈ 0. 8991

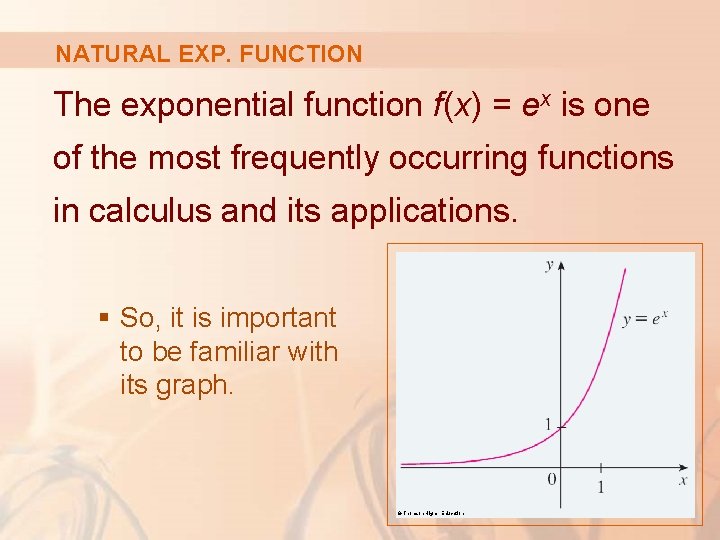
NATURAL EXP. FUNCTION The exponential function f(x) = ex is one of the most frequently occurring functions in calculus and its applications. § So, it is important to be familiar with its graph. © Thomson Higher Education

NATURAL EXP. FUNCTION It is also important to be familiar with its properties. § These follow from the fact that it is the inverse of the natural logarithmic function.

PROPERTIES Properties 6 The exponential function f(x) = ex is an increasing continuous function with domain and range (0, ∞). § Thus, e x > 0 for all x
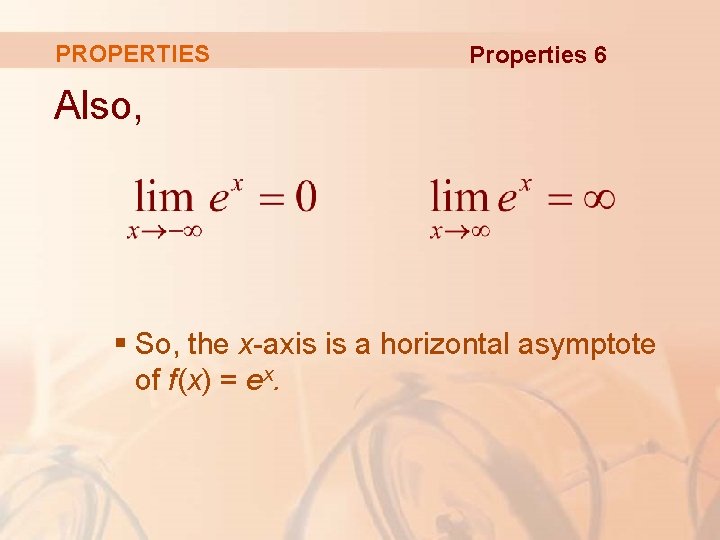
PROPERTIES Properties 6 Also, § So, the x-axis is a horizontal asymptote of f(x) = ex.

PROPERTIES Example 3 Find: § We divide numerator and denominator by e 2 x: § We have used the fact that t = -2 x → -∞ as x → ∞ and so

PROPERTIES Now, we verify that f(x) = ex has the properties expected of an exponential function.

LAWS OF EXPONENTS Laws 7 If x and y are real numbers and r is rational, then 1. e x+y = e xe y 2. e x-y = e x/e y 3. (e x)r = e rx

LAW 1 OF EXPONENTS Proof Using the first law of logarithms and Equation 5, we have: § Since ln is a one-to-one function, it follows that: e xe y = e x+y

LAWS 2 AND 3 OF EXPONENTS Laws 2 and 3 are proved similarly. § See Exercises 95 and 96. § As we will see in Section 7. 4*, Law 3 actually holds when r is any real number.

DIFFERENTIATION Formula 8 The natural exponential function has the remarkable property that it is its own derivative.

DIFFERENTIATION Formula 8—Proof The function y = ex is differentiable because it is the inverse function of y = ln x. § We know this is differentiable with nonzero derivative. To find its derivative, we use the inverse function method.

DIFFERENTIATION Formula 8—Proof Let y = ex. Then, ln y = x and, differentiating this latter equation implicitly with respect to x, we get:

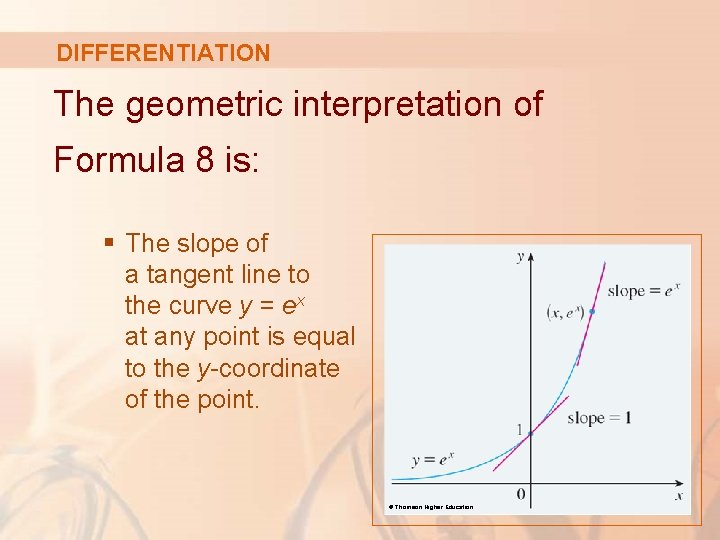
DIFFERENTIATION The geometric interpretation of Formula 8 is: § The slope of a tangent line to the curve y = ex at any point is equal to the y-coordinate of the point. © Thomson Higher Education

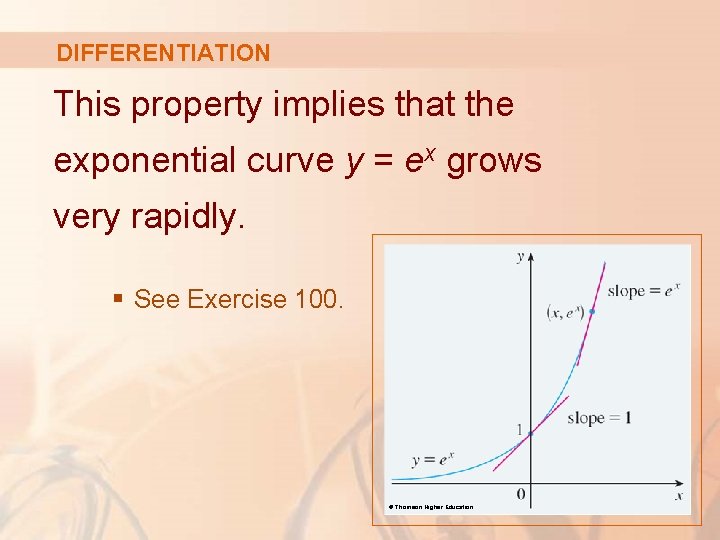
DIFFERENTIATION This property implies that the exponential curve y = ex grows very rapidly. § See Exercise 100. © Thomson Higher Education

DIFFERENTIATION Example 4 Differentiate the function y = e tan x. § To use the Chain Rule, we let u = tan x. § Then, we have y = e u. § Hence,

DIFFERENTIATION Formula 9 In general, if we combine Formula 8 with the Chain Rule, as in Example 4, we get:

DIFFERENTIATION Example 5 Find y’ if y = e-4 x sin 5 x. § Using Formula 9 and the Product Rule, we have:

DIFFERENTIATION Example 6 Find the absolute maximum value of the function f(x) = xe -x. § We differentiate to find any critical numbers: f’(x) = xe-x(-1) + e-x(1) = e-x(1 – x)

DIFFERENTIATION Example 6 Since exponential functions are always positive, we see that f ’(x) > 0 when 1 – x > 0, that is, when x < 1. Similarly, f ’(x) < 0 when x > 1.

DIFFERENTIATION Example 6 By the First Derivative Test for Absolute Extreme Values, f has an absolute maximum value when x = 1. § The absolute maximum value is:

DIFFERENTIATION Example 7 Use the first and second derivatives of f(x) = e 1/x, together with asymptotes, to sketch its graph. § Notice that the domain of f is {x | x ≠ 0}. § Hence, we check for vertical asymptotes by computing the left and right limits as x → 0.

DIFFERENTIATION Example 7 As x→ 0+, we know that t = 1/x → ∞. So, § This shows that x = 0 is a vertical asymptote.

DIFFERENTIATION Example 7 As x → 0 -, we know that t = 1/x →-∞. So, As x→ ∞, we have 1/x → 0. So, § This shows that y = 1 is a horizontal asymptote.

DIFFERENTIATION Example 7 Now, let’s compute the derivative. § The Chain Rule gives: § Since e 1/x > 0 and x 2 > 0 for all x ≠ 0, we have f ’(x) < 0 for all x ≠ 0. § Thus, f is decreasing on (-∞, 0) and on (0, ∞). § There is no critical number, so the function has no maximum or minimum.

DIFFERENTIATION Example 7 The second derivative is:

DIFFERENTIATION Example 7 Since e 1/x > 0 and x 4 > 0, we have f ”(x) > 0 when x > -½(x ≠ 0) and f ”(x) < 0 when x < -½. § So, the curve is concave downward on (-∞, -½) and concave upward on (-½, 0) and on (0, ∞). § The inflection point is (-½, e-2).

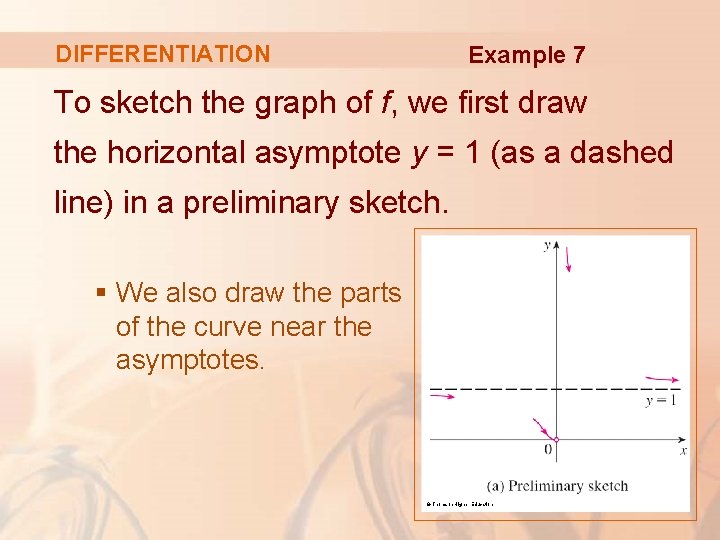
DIFFERENTIATION Example 7 To sketch the graph of f, we first draw the horizontal asymptote y = 1 (as a dashed line) in a preliminary sketch. § We also draw the parts of the curve near the asymptotes. © Thomson Higher Education

DIFFERENTIATION Example 7 These parts reflect the information concerning limits and the fact that f is decreasing on both (-∞, 0) and (0, ∞). § Notice that we have indicated that f(x) → 0 as x → 0 - even though f(0) does not exist. © Thomson Higher Education

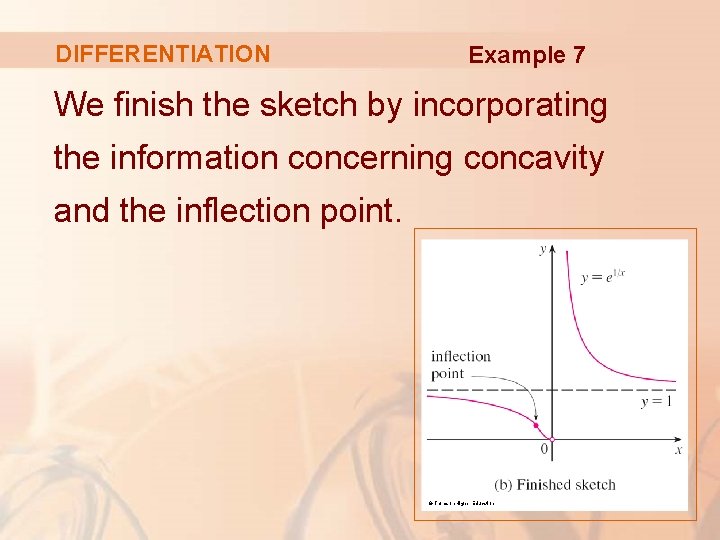
DIFFERENTIATION Example 7 We finish the sketch by incorporating the information concerning concavity and the inflection point. © Thomson Higher Education

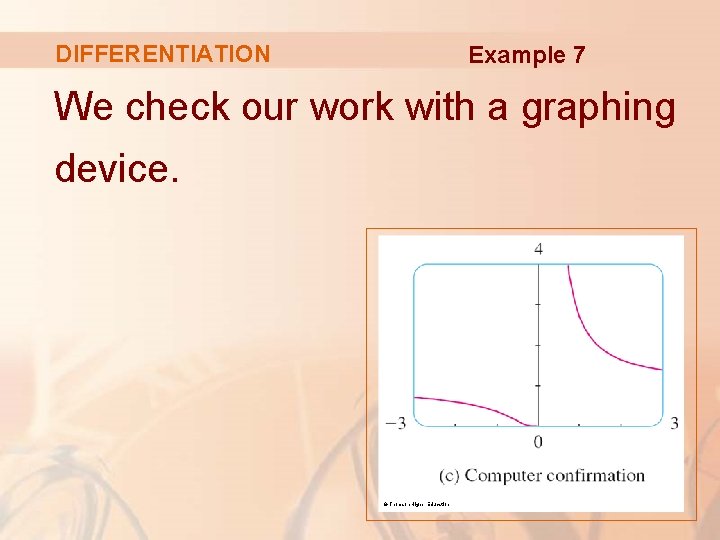
DIFFERENTIATION Example 7 We check our work with a graphing device. © Thomson Higher Education

INTEGRATION Formula 10 As the exponential function y = ex has a simple derivative, its integral is also simple:

INTEGRATION Example 8 Evaluate: § We substitute u = x 3. § Then, du = 3 x 2 dx. § So, and

INTEGRATION Example 9 Find the area under the curve y = e-3 x from 0 to 1. § The area is:
 Phản ứng thế ankan
Phản ứng thế ankan ưu thế lai là gì
ưu thế lai là gì Thẻ vin
Thẻ vin Môn thể thao bắt đầu bằng từ đua
Môn thể thao bắt đầu bằng từ đua Cái miệng bé xinh thế chỉ nói điều hay thôi
Cái miệng bé xinh thế chỉ nói điều hay thôi Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Tư thế ngồi viết
Tư thế ngồi viết Chó sói
Chó sói Thế nào là giọng cùng tên?
Thế nào là giọng cùng tên? Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Sự nuôi và dạy con của hươu
Sự nuôi và dạy con của hươu đại từ thay thế
đại từ thay thế Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Diễn thế sinh thái là
Diễn thế sinh thái là Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Lp html
Lp html Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi Mật thư anh em như thể tay chân
Mật thư anh em như thể tay chân Lời thề hippocrates
Lời thề hippocrates Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Tư thế worms-breton
Tư thế worms-breton Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Khi nào hổ mẹ dạy hổ con săn mồi
Khi nào hổ mẹ dạy hổ con săn mồi điện thế nghỉ
điện thế nghỉ Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Các loại đột biến cấu trúc nhiễm sắc thể
Các loại đột biến cấu trúc nhiễm sắc thể Thế nào là sự mỏi cơ
Thế nào là sự mỏi cơ Bổ thể
Bổ thể 101012 bằng
101012 bằng Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan Tia chieu sa te
Tia chieu sa te Hát lên người ơi
Hát lên người ơi Một số thể thơ truyền thống
Một số thể thơ truyền thống Sơ đồ cơ thể người
Sơ đồ cơ thể người Số nguyên tố là
Số nguyên tố là Tư thế ngồi viết
Tư thế ngồi viết Công thức tính độ biến thiên đông lượng
Công thức tính độ biến thiên đông lượng Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Chapter 5 logarithmic exponential and other
Chapter 5 logarithmic exponential and other 1-7 inverse relations and functions
1-7 inverse relations and functions How to find angle with inverse trig
How to find angle with inverse trig 1-4 inverses of functions
1-4 inverses of functions Inverse circular functions
Inverse circular functions Define inverse of a function with an arrow diagram
Define inverse of a function with an arrow diagram







































































