O G M O E I R T

O G M O E I R T M A E VA 2018/2019

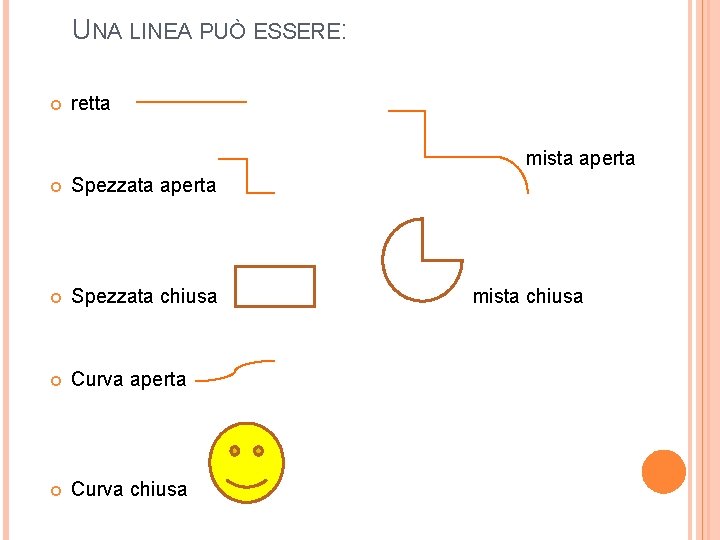
UNA LINEA PUÒ ESSERE: retta mista aperta Spezzata chiusa Curva aperta Curva chiusa mista chiusa

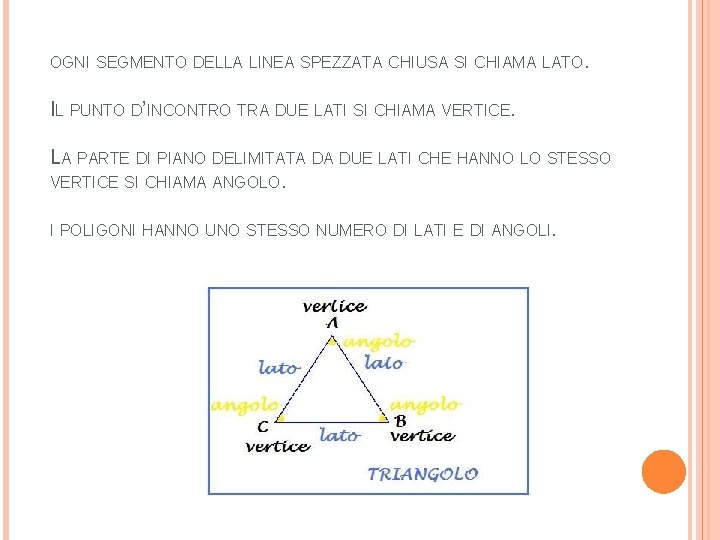
OGNI SEGMENTO DELLA LINEA SPEZZATA CHIUSA SI CHIAMA LATO. IL PUNTO D’INCONTRO TRA DUE LATI SI CHIAMA VERTICE. LA PARTE DI PIANO DELIMITATA DA DUE LATI CHE HANNO LO STESSO VERTICE SI CHIAMA ANGOLO. I POLIGONI HANNO UNO STESSO NUMERO DI LATI E DI ANGOLI.

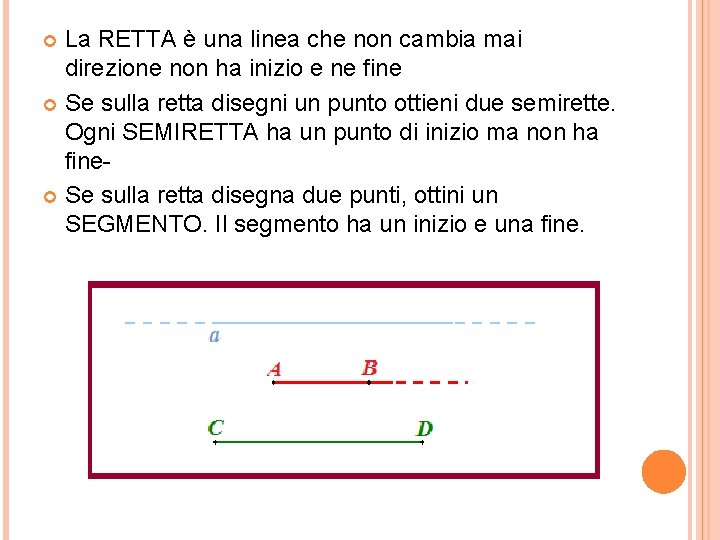
La RETTA è una linea che non cambia mai direzione non ha inizio e ne fine Se sulla retta disegni un punto ottieni due semirette. Ogni SEMIRETTA ha un punto di inizio ma non ha fine Se sulla retta disegna due punti, ottini un SEGMENTO. Il segmento ha un inizio e una fine.

La posizione di una retta sul piano può essere: ORIZZONTALE, VERTICALE O OBLIQUA Due o più rette su un piano possono essere tre loro: PARALLELE, INCIDENTI O PERPENDICOLARI Le rette PARALLELE mantengono la stessa distanza e non si incontrano mai Le rette INCIDENTI si incontrano in un punto e formano 4 angoli, uguali a due Le rette PERPENDICOLARI sono un tipo particolare di rette incidenti perché incontrandosi formano 4 angoli tutti uguali (retti)

L’ANGOLO È la parte di piano compresa da due semirette che hanno lo stesso punto di origine (vertice). Gli angoli si misurano in GRADI (simbolo ° ). Lo strumento di misura è il GONIOMETRO. 1° = 1/360 dell’angolo giro.

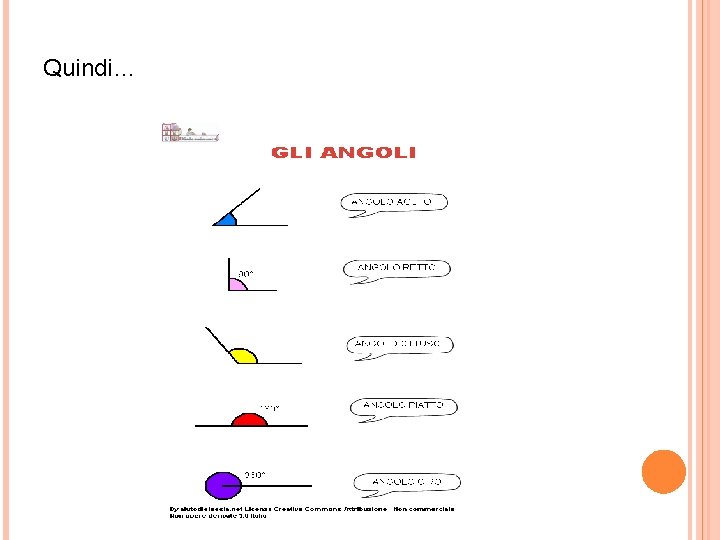
Quindi…

L’angolo giro misura 360° L’angolo piatto misura 180° L’angolo retto misura 90° L’angolo acuto misura meno di 90° L’angolo ottuso misura più di 90° e meno di 180° L’angolo concavo misura di 180° ma meno di 360° Tutti gli angoli minori 180° (cioè acuti, retti, ottusi ) si dicono convessi.

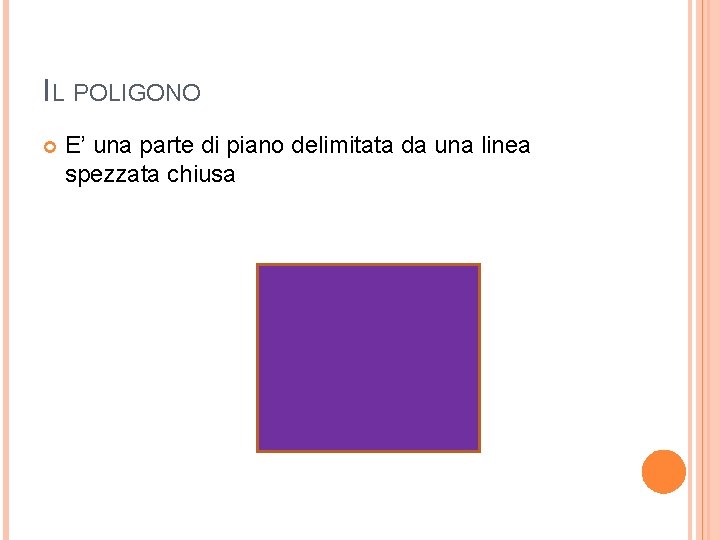
IL POLIGONO E’ una parte di piano delimitata da una linea spezzata chiusa

I POLIGONI LA PAROLA POLIGONO VIENE DAL GRECO: POLI=TANTI E GONON=ANGOLI, QUINDI SIGNIFICA TANTI ANGOLI. IN TUTTI I POLIGONI IL NUMERO DEI LATI E’ UGUALE AL NUMERO DEGLI ANGOLI E DEI VERTICI. NON CI SONO POLIGONI CON MENO DI 3 LATI.

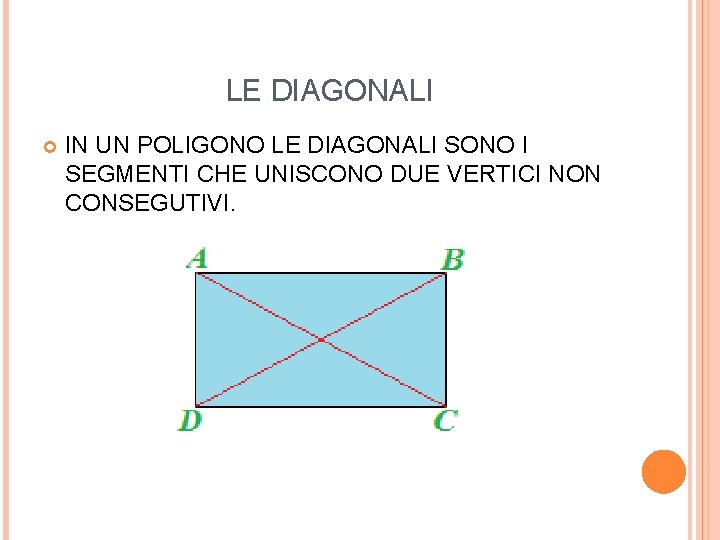
LE DIAGONALI IN UN POLIGONO LE DIAGONALI SONO I SEGMENTI CHE UNISCONO DUE VERTICI NON CONSEGUTIVI.

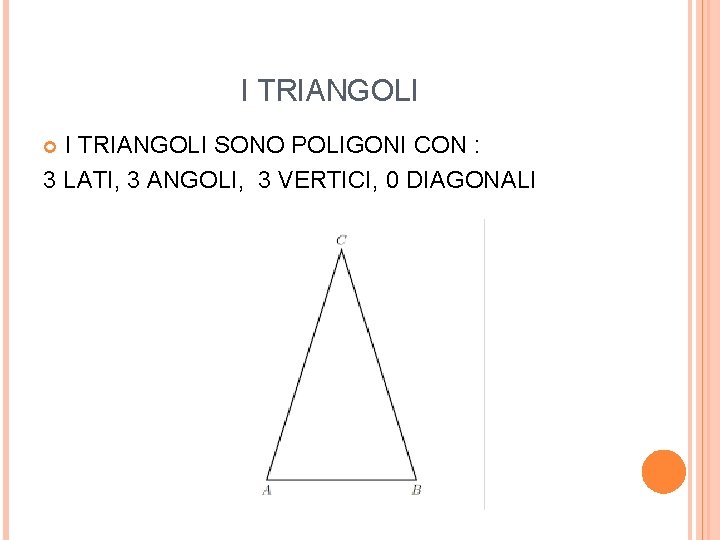
I TRIANGOLI SONO POLIGONI CON : 3 LATI, 3 ANGOLI, 3 VERTICI, 0 DIAGONALI

CLASSIFICHIAMI I TRIANGOLI GUARDANDO GLI ANGOLI TRIANGOLO RETTANGOLO: HA UN ANGOLO RETTO TRIANGOLO OTTUSANGOLO: HA UN ANGOLO OTTUSO TRIANGOLO ACUTANGOLO: HA TUTTI GLI ANGOLI ACUTI

CLASSIFICHIAMO I TRIANGOLI GUARDANDO I LATI: TRIANGOLO EQUILATERO: HA I 3 LATI UGUALI TRIANGOLO ISOSCELE: HA 2 LATI UGUALI TRIANGOLO SCALENO: HA I 3 LATI DIVERSI TRA LORO

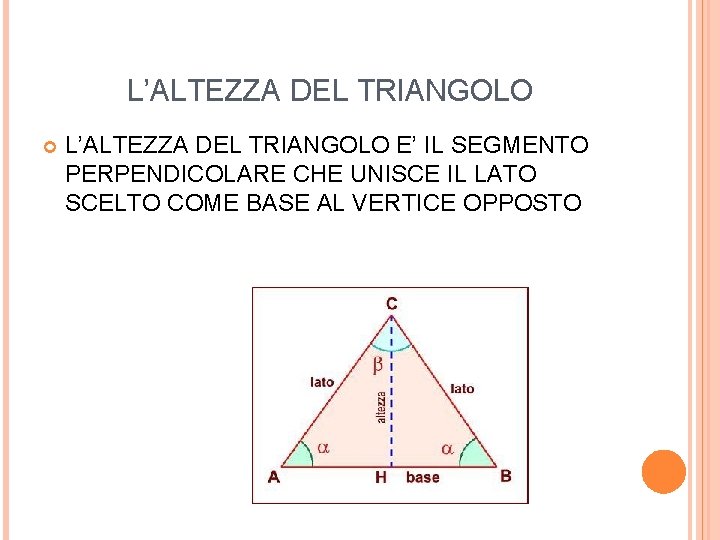
L’ALTEZZA DEL TRIANGOLO E’ IL SEGMENTO PERPENDICOLARE CHE UNISCE IL LATO SCELTO COME BASE AL VERTICE OPPOSTO

LA SOMMA DEGLI ANGOLI INTERNI DI UN TRIANGOLO E’ SEMPRE DI 180°. DUNQUE UN TRIANGOLO EQUILATERO (CHE HA I 3 LATI E I 3 ANGOLI UGUALI) HA OGNI ANGOLO DI 60°

I QUADRILATERI sono poligoni con: 4 lati, 4 angoli, 2 diagonali. La somma degli angoli interni di un quadrilatero è sempre 360°.

I quadrilateri che hanno almeno una coppia di lati paralleli sono TRAPEZI (anche se comunemente si dicono TRAPEZI i quadrilateri che hanno solo una coppia di lati paralleli. )

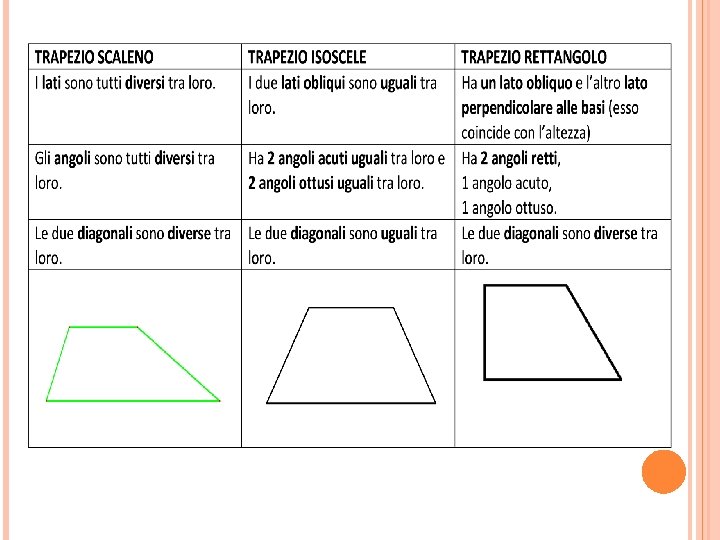
I due lati paralleli si chiamano BASI: la più lunga è la base maggiore, la più corta è la base minore. Gli altri due si dicono lati obliqui. Il segmento perpendicolare alle due basi è l’altezza (h). I segmenti che uniscono due vertici non consecutivi si chiamano diagonali (d). Le due diagonali possono essere di lunghezza uguale o diversa tra loro, ma incrociandosi non si tagliano mai a metà e non formano angoli retti.

I PARALLELOGRAMMI ( o ROMBOIDI) sono quadrilateri con due coppie di lati paralleli. I lati opposti sono uguali e paralleli (possiamo anche dire che i lati sono a due uguali e paralleli) Gli angoli opposti sono uguali: ci sono 2 angoli acuti della stessa ampiezza e 2 angoli ottusi della stessa ampiezza. Le 2 diagonali sono diverse, incrociandosi si tagliano a metà, ma non formano angoli retti. L’altezza è il segmento perpendicolare alle basi. (attenzione però ai «parallelogrammi speciali»

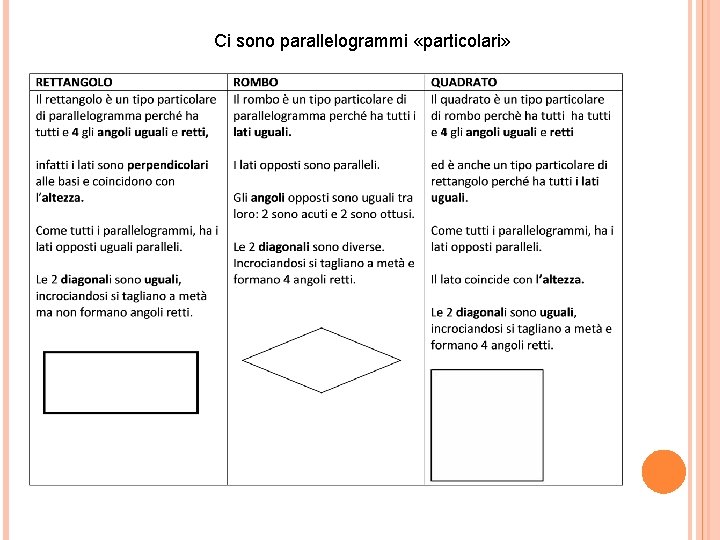
Ci sono parallelogrammi «particolari»

I POLIGONIEQUILATERI hanno tutti i lati uguali. Tra quelli studiati fin ora sono: TRIANGOLO EQUILATERO, QUADRATO, ROMBO.

I POLIGONI EQUIANGOLI HANNO TUTTI GLI ANGOLI UGUALI. TRA QUELLI STUDIATI FINORA SONO: TRIANGOLO EQUILATERO(60°), QUADRATO(90°) RETTANGOLO(90°)

I POLIGONI REGOLARI SONO QUELLI SIA EQUILATERI CHE EQUIANGOLI, CHE CIOE’ HANNO TUTTI I LATI E TUTTI GLI ANGOLI UGUALI. TRA QUELLI STUDIATI FINORA SONO: TRIANGOLO EQUILATERO, QUADRATO.

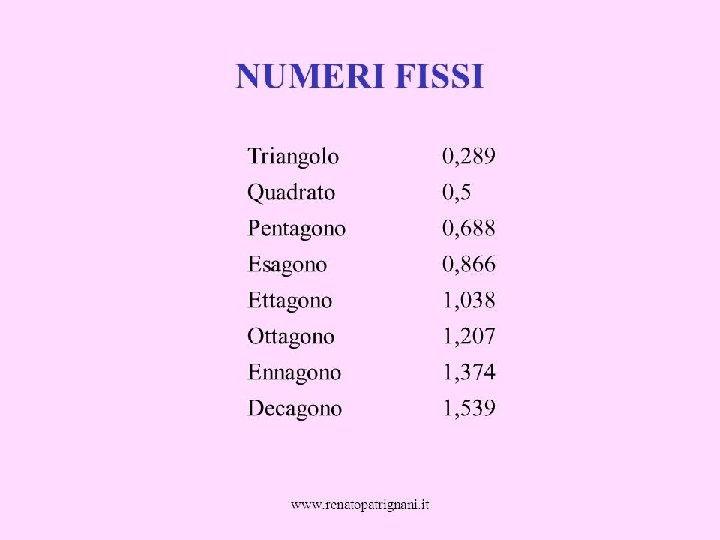
POLIGONI REGOLARI CON PIU’ DI 4 LATI: Pentagono regolare: 5 lati e 5 angoli congruenti Esagono regolare: 6 lati e 6 angoli congruenti Ettagono regolare: 7 lati e 7 angoli congruenti Ottagono regolare: 8 lati e 8 angoli congruenti Ennagono regolare: 9 lati e 9 angoli congruenti Decagono regolare: 10 lati e 10 angoli congruenti Etc…

L’APOTEMA Tutti i poligoni regolari hanno l’apotema. L’apotema è il segmento perpendicolare che unisce il centro del poligono a ciascun lato. L’apotema divide ciascun lato in due parti uguali. apotema= lato x numero fisso

IL PERIMETRO È LA MISURA DEL CONTORNO DI UNA FIGURA PIANA, CIOE’ DEL SUO CONFINE. SI CALCOLA FACENDO LA SOMMA DEI LATI

L’AREA L’area di una figura è la misura della superficie, cioè della sua regione interna. L’unità di misura è il metro quadrato (con i suoi multipli e sottomultipli che si ottengono moltiplicando o dividendo per 100, 1000000)

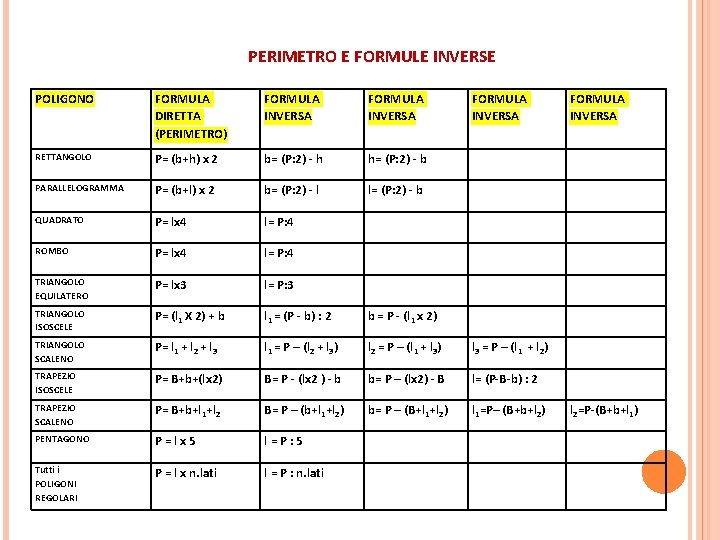
PERIMETRO E FORMULE INVERSE POLIGONO FORMULA DIRETTA (PERIMETRO) FORMULA INVERSA RETTANGOLO P= (b+h) x 2 b= (P: 2) - h h= (P: 2) - b PARALLELOGRAMMA P= (b+l) x 2 b= (P: 2) - l l= (P: 2) - b QUADRATO P= lx 4 l= P: 4 ROMBO P= lx 4 l= P: 4 TRIANGOLO EQUILATERO P= lx 3 l= P: 3 TRIANGOLO ISOSCELE P= (l 1 X 2) + b l 1 = (P - b) : 2 b = P - (l 1 x 2) TRIANGOLO SCALENO P= l 1 + l 2 + l 3 l 1 = P – (l 2 + l 3) l 2 = P – (l 1 + l 3) l 3 = P – (l 1 + l 2) TRAPEZIO ISOSCELE P= B+b+(lx 2) B= P - (lx 2 ) - b b= P – (lx 2) - B l= (P-B-b) : 2 TRAPEZIO SCALENO P= B+b+l 1+l 2 B= P – (b+l 1+l 2) b= P – (B+l 1+l 2) l 1=P– (B+b+l 2) l 2=P-(B+b+l 1) PENTAGONO P = l x 5 l = P : 5 Tutti i POLIGONI REGOLARI P = l x n. lati l = P : n. lati

AREA E FORMULE INVERSE POLIGONO FORMULA DIRETTA (AREA) FORMULA INVERSA RETTANGOLO A= b x h PARALLELOGRAMMA A= b x h b= A : h h= A : b QUADRATO A= l x l La scoprirai l’anno prossimo… TRIANGOLO ROMBO TRAPEZIO PENTAGONO e gli altri poligoni regolari A= (bxh) : 2 b= (Ax 2) : h h= (Ax 2) : b A= (Dxd) : 2 D= (Ax 2) : d d= (Ax 2) : D A= (B+b) x h : 2 B= (A x 2 : h) - b b= (A x 2 : h) - B h= (Ax 2) : (B+b) A= (P x a) : 2 P= (A x 2) : a a= (A x 2) : P

IL CERCHIO è un NON POLIGONO. E’ una parte di piano delimitata da una linea curva chiusa detta CIRCONFERENZA. Potremmo dire, per intenderci, che la circonferenza è il perimetro del cerchio. La circonferenza ha una caratteristica: tutti i suoi punti sono equidistanti dal centro. Il segmento che va dal centro a un punto qualsiasi della circonferenza si chiama RAGGIO. Tutti i raggi di un cerchio hanno la stessa misura.

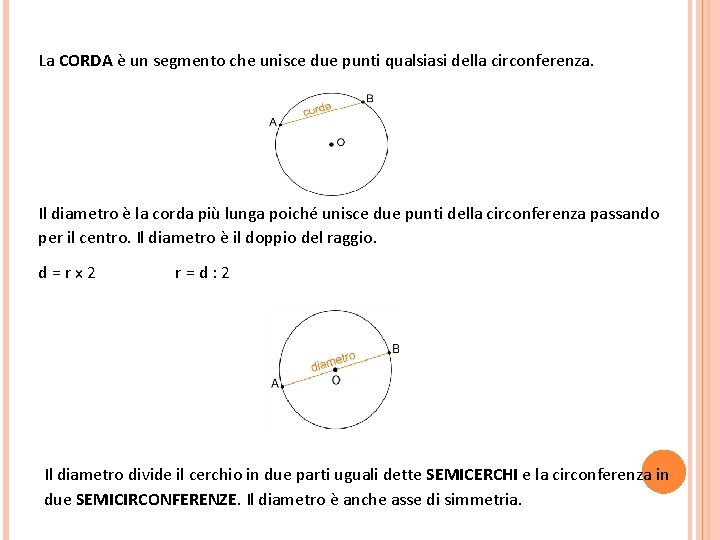
La CORDA è un segmento che unisce due punti qualsiasi della circonferenza. Il diametro è la corda più lunga poiché unisce due punti della circonferenza passando per il centro. Il diametro è il doppio del raggio. d = r x 2 r = d : 2 Il diametro divide il cerchio in due parti uguali dette SEMICERCHI e la circonferenza in due SEMICIRCONFERENZE. Il diametro è anche asse di simmetria.

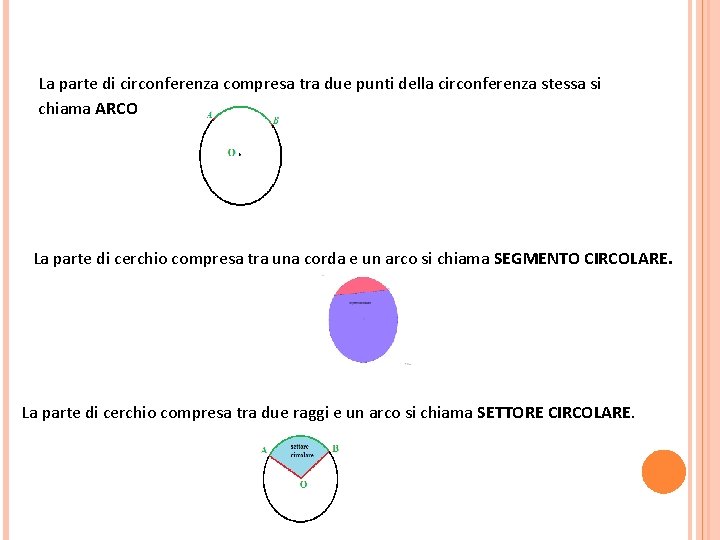
La parte di circonferenza compresa tra due punti della circonferenza stessa si chiama ARCO La parte di cerchio compresa tra una corda e un arco si chiama SEGMENTO CIRCOLARE. La parte di cerchio compresa tra due raggi e un arco si chiama SETTORE CIRCOLARE.

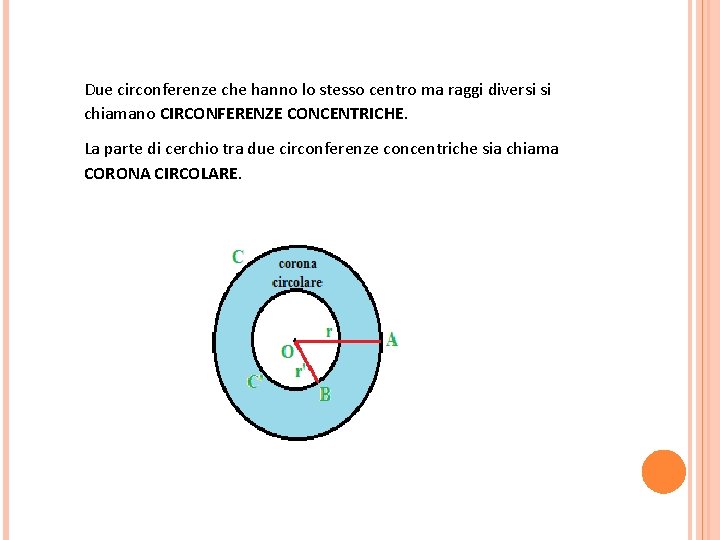
Due circonferenze che hanno lo stesso centro ma raggi diversi si chiamano CIRCONFERENZE CONCENTRICHE. La parte di cerchio tra due circonferenze concentriche sia chiama CORONA CIRCOLARE.

PI GRECO Anche il cerchio ha il numero fisso. Nel III Sec. A. C. Archimede, un matematico della Magna Grecia, osservò che ogni diametro è contenuto nella sua circonferenza 3 volte e un po’, più precisamente 3, 1415927…. Questo numero è irrazionale, cioè decimale illimitato non periodico, pertanto viene approssimato ai centesimi: 3, 14. I matematici gli hanno dato un nome: PI GRECO

MISURA DELLA CIRCONFERENZA C = d x 3, 14 Oppure C = r x 2 x 3, 14 FORMULE INVERSE: d = C : 3, 14 r = (C : 3, 14) : 2 oppure r = C : 6, 28

AREA DEL CERCHIO A=Cxr: 2 Oppure A = r x 3, 14

IL VOLUME Le figure solide occupano uno spazio e hanno 3 dimensioni: lunghezza, larghezza e altezza. I solidi si dividono in POLIEDRI e SOLIDI DI ROTAZIONE. Lo spazio occupato da un solido si dice VOLUME. L’unità di misura del volume è il metro cubo (m 3) , cioè un cubo con ogni dimensione di 1 m. L’esponente 3 indica proprio le 3 dimensioni. Il m 3 ha multipli e sottomultipli che si ottengono moltiplicando o dividendo per 1000, 1000000000. Misurare il volume vuol dire stabilire quante volte l’unità di misura è contenuta nel solido, ma per semplificare possiamo usare delle formule.

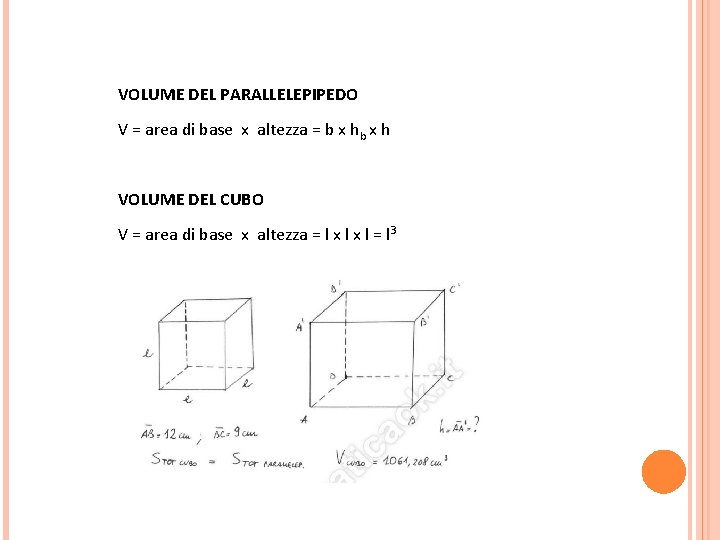
VOLUME DEL PARALLELEPIPEDO V = area di base x altezza = b x h VOLUME DEL CUBO V = area di base x altezza = l x l = l 3