Additionneurs 1 Rappel sur lcriture des entiers en

Additionneurs 1

Rappel sur l'écriture des entiers en base 2 • Entiers positifs • Entiers relatifs (complément à 2) 2

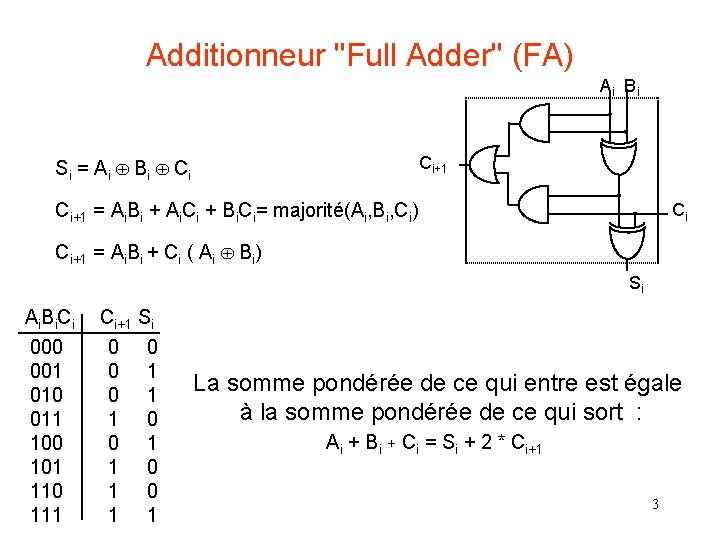
Additionneur "Full Adder" (FA) Ai Bi Si = Ai Bi Ci+1 = Ai. Bi + Ai. Ci + Bi. Ci= majorité(Ai, Bi, Ci) Ci Ci+1 = Ai. Bi + Ci ( Ai Bi) Si Ai. Bi. Ci Ci+1 Si 000 0 0 001 0 1 010 0 1 011 1 0 100 0 1 101 1 0 110 1 0 111 1 1 La somme pondérée de ce qui entre est égale à la somme pondérée de ce qui sort : Ai + Bi + Ci = Si + 2 * Ci+1 3

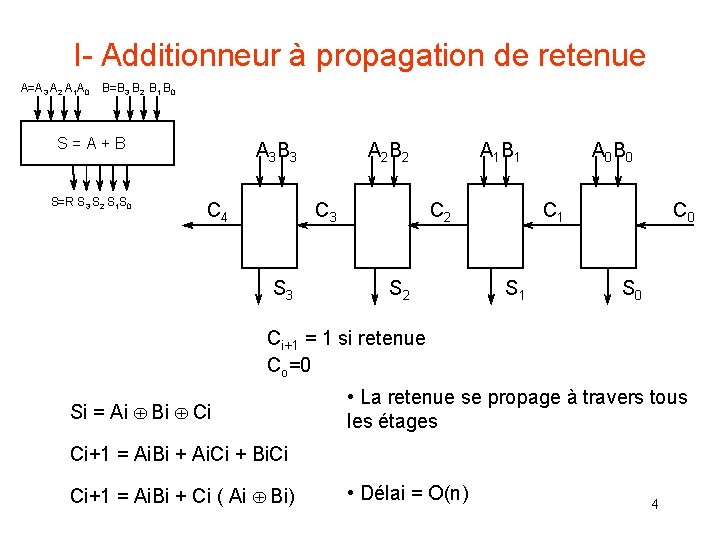
I- Additionneur à propagation de retenue A=A 3 A 2 A 1 A 0 B=B 3 B 2 B 1 B 0 S = A + B S=R S 3 S 2 S 1 S 0 A 3 B 3 C 4 A 2 B 2 C 3 S 3 A 1 B 1 C 2 S 2 A 0 B 0 C 1 S 1 C 0 S 0 Ci+1 = 1 si retenue Co=0 Si = Ai Bi Ci • La retenue se propage à travers tous les étages Ci+1 = Ai. Bi + Ai. Ci + Bi. Ci Ci+1 = Ai. Bi + Ci ( Ai Bi) • Délai = O(n) 4

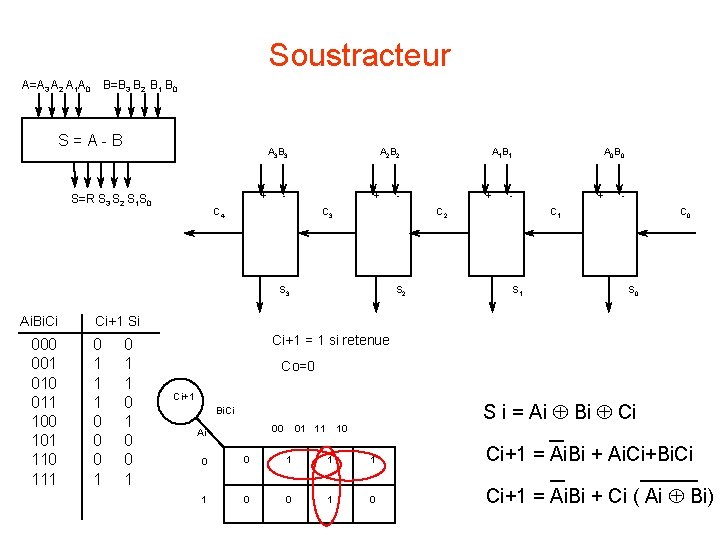
Soustracteur A=A 3 A 2 A 1 A 0 B=B 3 B 2 B 1 B 0 S = A - B A 3 B 3 + S=R S 3 S 2 S 1 S 0 A 2 B 2 - C 4 + - C 3 + S 2 A 0 B 0 - C 2 S 3 Ai. Bi. Ci A 1 B 1 + - C 1 S 1 C 0 S 0 Ci+1 Si 000 0 0 001 1 1 010 1 1 011 1 0 100 0 1 101 0 0 110 0 0 111 1 1 Ci+1 = 1 si retenue Co=0 Ci+1 S i = Ai Bi Ci Bi. Ci 00 01 10 Ai 0 0 1 1 1 Ci+1 = Ai. Bi + Ai. Ci+Bi. Ci 1 0 0 1 0 Ci+1 = Ai. Bi + Ci ( Ai Bi)

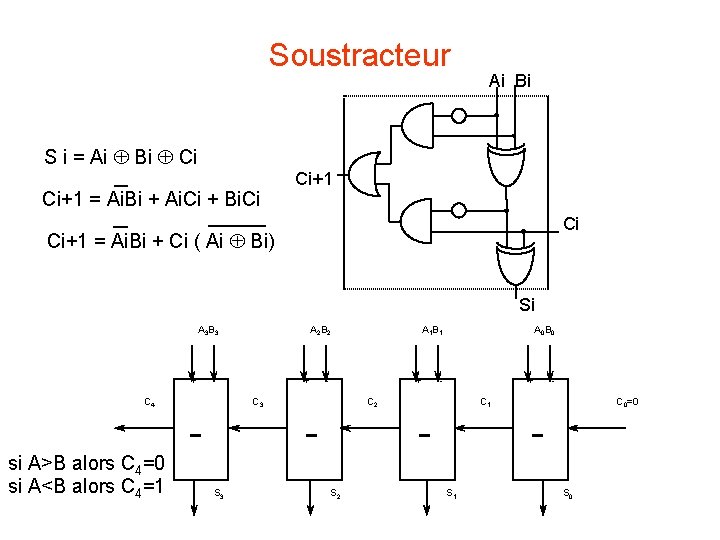
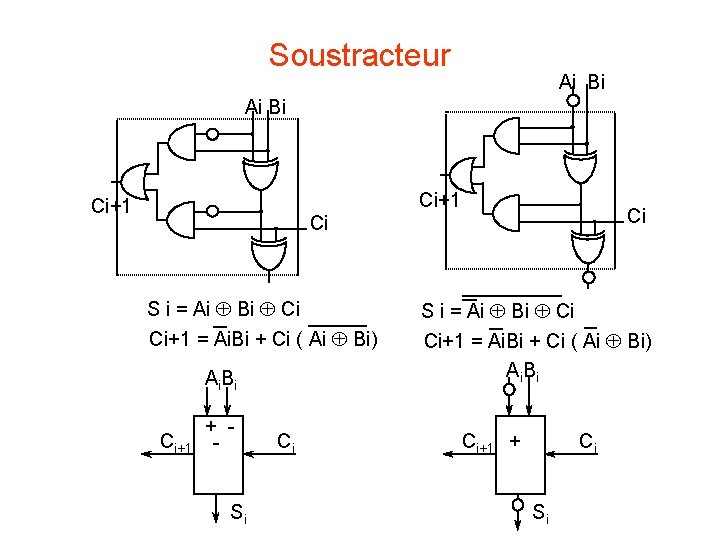
Soustracteur S i = Ai Bi Ci Ci+1 = Ai. Bi + Ai. Ci + Bi. Ci Ai Bi Ci+1 Ci Ci+1 = Ai. Bi + Ci ( Ai Bi) Si A 3 B 3 + - C 4 si A>B alors C 4=0 si A<B alors C 4=1 A 2 B 2 + - + C 3 - A 0 B 0 - + C 2 S 3 A 1 B 1 C 1 S 2 C 0=0 S 1 S 0

Soustracteur Ai Bi Ci+1 Ci Ci S i = Ai Bi Ci Ci+1 = Ai. Bi + Ci ( Ai Bi) Ai. Bi Ci+1 + Si Ci S i = Ai Bi Ci Ci+1 = Ai. Bi + Ci ( Ai Bi) Ai. Bi Ci+1 + Ci Si

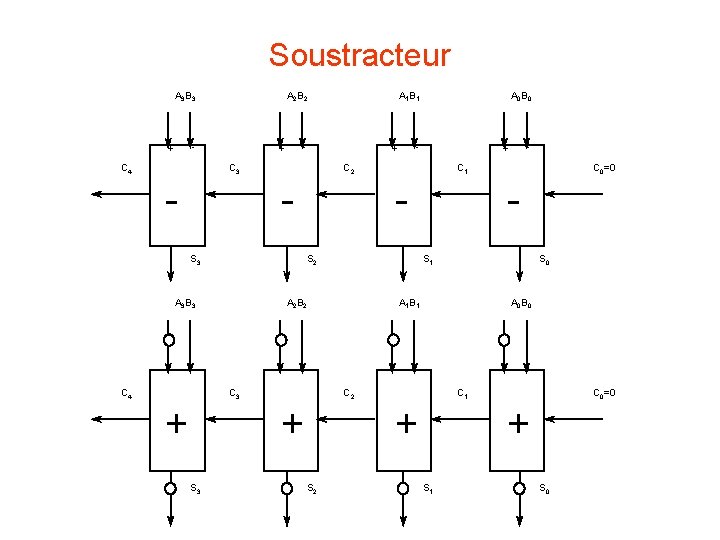
Soustracteur A 3 B 3 A 2 B 2 - + C 4 - + S 3 C 4 + S 2 S 0 A 1 B 1 A 0 B 0 C 2 C 1 + S 2 C 0=0 S 1 A 2 B 2 + S 3 C 1 - C 3 - + C 2 - A 3 B 3 A 0 B 0 - + C 3 - A 1 B 1 C 0=0 + S 1 S 0

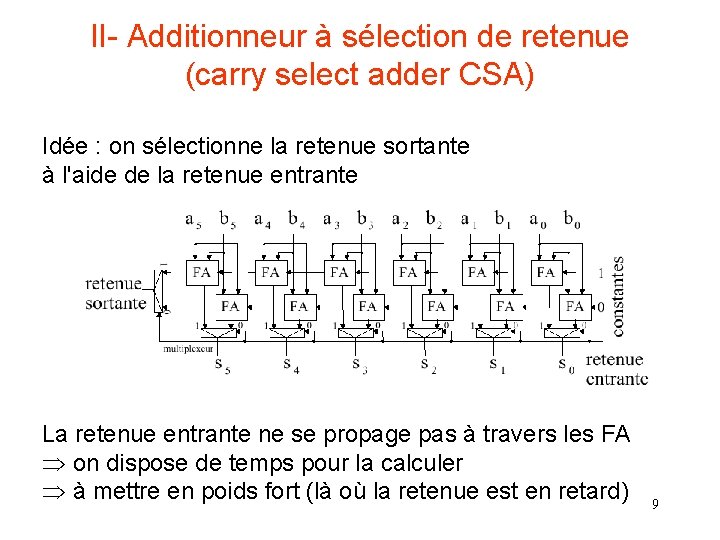
II- Additionneur à sélection de retenue (carry select adder CSA) Idée : on sélectionne la retenue sortante à l'aide de la retenue entrante La retenue entrante ne se propage pas à travers les FA Þ on dispose de temps pour la calculer Þ à mettre en poids fort (là où la retenue est en retard) 9

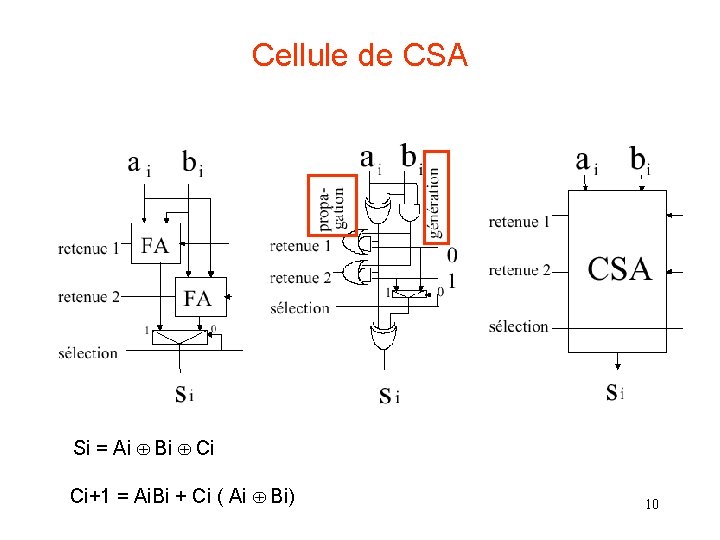
Cellule de CSA Si = Ai Bi Ci Ci+1 = Ai. Bi + Ci ( Ai Bi) 10

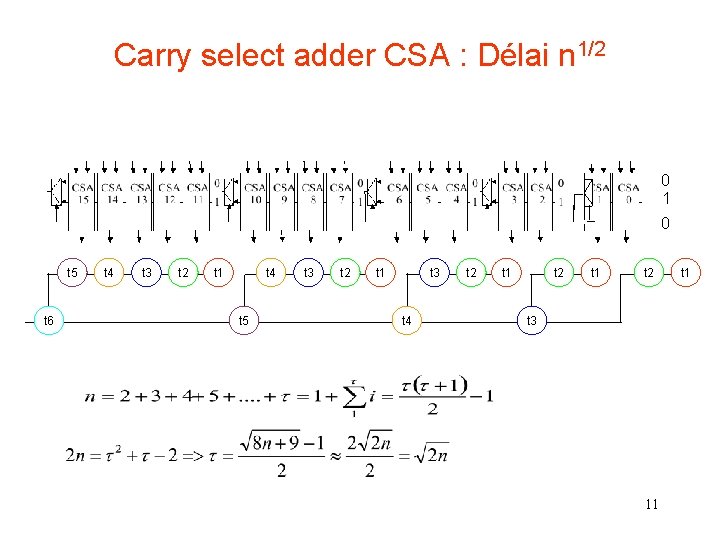
Carry select adder CSA : Délai n 1/2 0 1 0 t 5 t 6 t 4 t 3 t 2 t 1 t 4 t 5 t 3 t 2 t 1 t 3 t 4 t 2 t 1 t 2 t 3 11 t 1

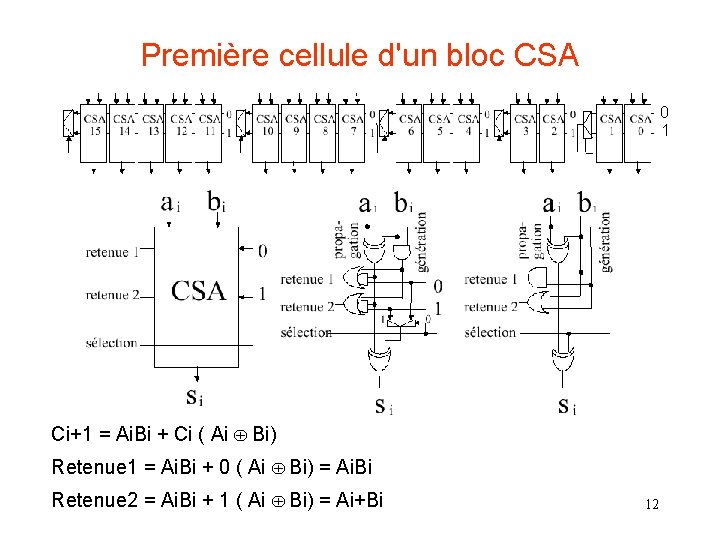
Première cellule d'un bloc CSA 0 1 • x Ci+1 = Ai. Bi + Ci ( Ai Bi) Retenue 1 = Ai. Bi + 0 ( Ai Bi) = Ai. Bi Retenue 2 = Ai. Bi + 1 ( Ai Bi) = Ai+Bi 12

III Additionneur à retenue bondissante (Carry Skip Adder) • Idée : Si Ai=Bi=0, Ci+1=0 : pas de retenue quelque soit Ci Si Ai=Bi=1, Ci+1=1 : il y a forcément une retenue, quelque soit Ci Si Ai≠Bi, , la retenue sortante de l’étage i est égale à la retenue entrante • Par blocs de p bits : – De même, la retenue sortante de l’étage i est égale à la retenue entrante si et seulement si les Apbits sont les inverses des Bpbits 01101 + 10010 + Cin ------Cin Somme – Dans les autres cas, la retenue sortante peut être calculée indépendamment de la retenue entrante 13

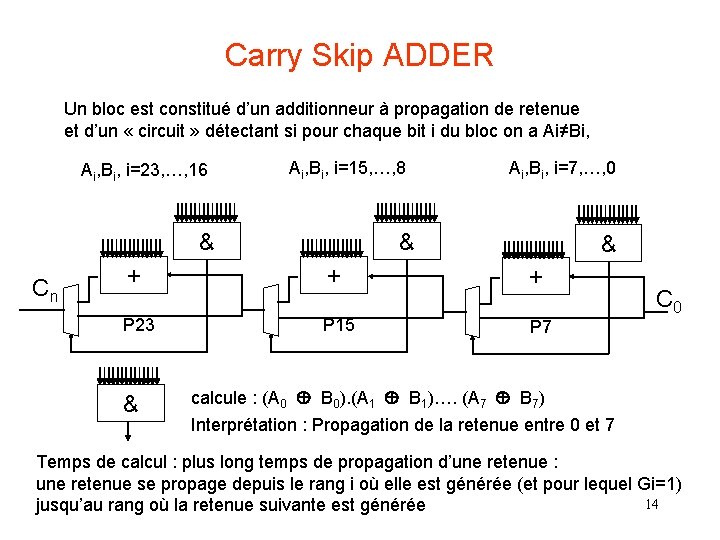
Carry Skip ADDER Un bloc est constitué d’un additionneur à propagation de retenue et d’un « circuit » détectant si pour chaque bit i du bloc on a Ai≠Bi, Ai, Bi, i=23, …, 16 Ai, Bi, i=15, …, 8 & Cn Ai, Bi, i=7, …, 0 & & + + + P 23 P 15 P 7 & C 0 calcule : (A 0 B 0). (A 1 B 1)…. (A 7 B 7) Interprétation : Propagation de la retenue entre 0 et 7 Temps de calcul : plus long temps de propagation d’une retenue : une retenue se propage depuis le rang i où elle est générée (et pour lequel Gi=1) 14 jusqu’au rang où la retenue suivante est générée

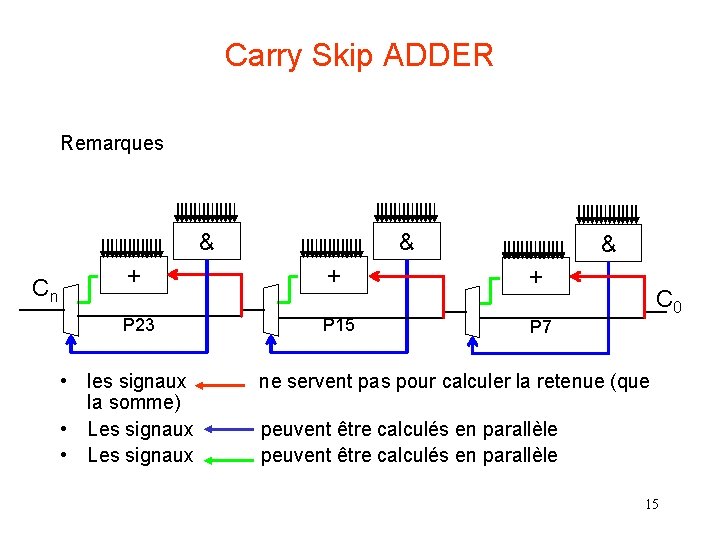
Carry Skip ADDER Remarques & Cn & & + + + P 23 P 15 P 7 C 0 • les signaux ne servent pas pour calculer la retenue (que la somme) • Les signaux peuvent être calculés en parallèle 15

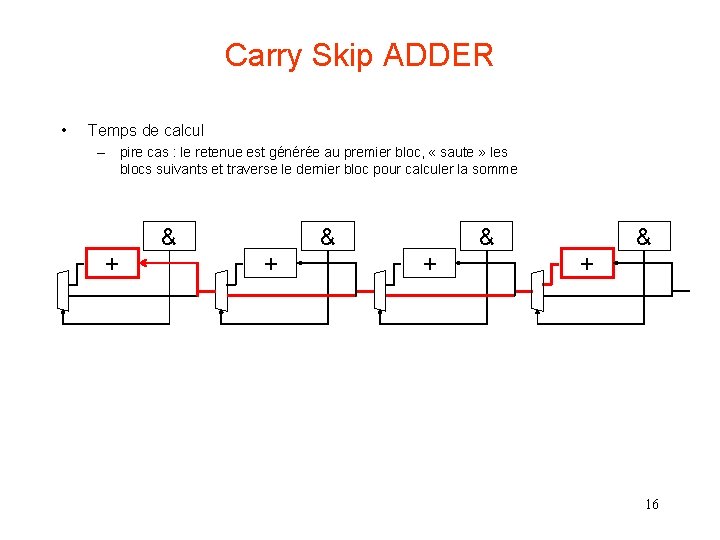
Carry Skip ADDER • Temps de calcul – pire cas : le retenue est générée au premier bloc, « saute » les blocs suivants et traverse le dernier bloc pour calculer la somme + & + & 16

Taille des blocs • Hypothèse: Groupes de même taille k , m=n/k groupes , k et n/k entiers • k sélectionné pour minimiser le temps de la plus longue chaîne de propagation temps de traversée d’un bloc de k additionneurs 1 bit : t 1*k temps de propagation à l'aide des comparateurs: t 2 ("mux") Temps total (pire cas) : 2*t 1*k + (m-2)*t 2 = 2* t 1 * n/m + (m-2) * t 2 • Il suffit de déterminer où cette fonction est minimale. 17

Carry Skip ADDER : taille des blocs Sous hypothèse 1 : le temps de propagation à travers les comparateurs est constant soit f(x) : 2*t 1*n/x + (x-2) * t 2 minimum pour x 0 = (2*n*t 1/t 2)1/2 f convexe sur R+ => m optimal : 2 valeurs entières qui encadrent x 0 Temps total = O(n 1/2) exemple : additionneur de 60 bits, t 1=t 2 => x 0=1201/2=10, 95 Þ m = 10 ou m =12 Þ 10 blocs de 6 bits ou 12 blocs de 5 bits 18

Carry Skip ADDER : taille des blocs • Hypothèse: Groupes de même taille k , m=n/k groupes , k et n/k entiers • k sélectionné pour minimiser le temps de la plus longue chaîne de propagation • Notations: – tr - temps de propagation de la retenue sur un seul bit – ts(k) – Temps pour sauter un groupe taille k (la plupart du temps - indépendant de k) – tb – délai du "MUX" entre 2 groupes – Ttotal – temps total de propagation de la retenue – lorsque la retenue est générée à l'étage 0 et se propage jusqu'à l'étage n-1 • La retenue se propage dans les étages 1, 2, … , k-1 du groupe 1, saute les groupes 2, 3, … , m-1, et se propage dans le groupe m 19

Carry Skip ADDER : taille des blocs • Ttotal=(k-1)tr+tb+(m-2)(ts+tb)+(k-1)tr • Exemple - implémentation 2 niveaux – tr = ts+tb = 2 G ( G = délai d'une porte) – Ttotal=(4 k+2 n/k-7) G • En dérivant Ttotal par rapport à k et en égalisant à 0 • kopt = n/2 • Taille des groupes et temps de propagation de la retenue proportionnel à n - idem carry-select adder • Exemple : n=32, 8 groupes de taille kopt = 4 est la meilleure solution • Topt=25 G au lieu 62 G pour un additionneur à propagation de retenue 20

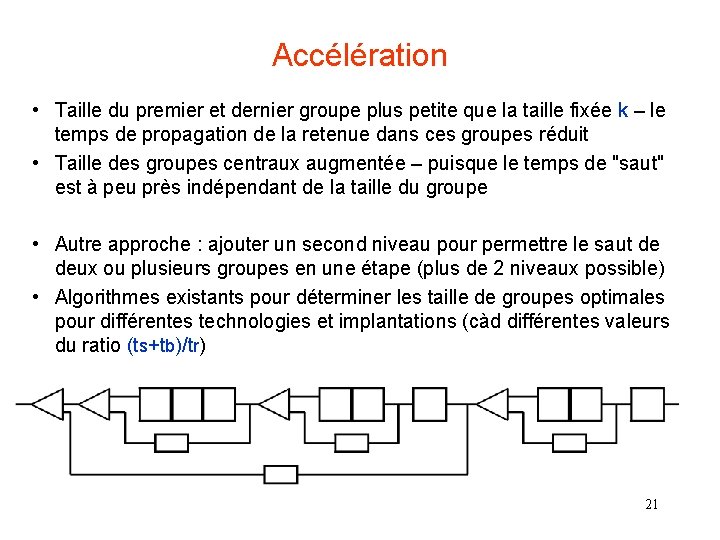
Accélération • Taille du premier et dernier groupe plus petite que la taille fixée k – le temps de propagation de la retenue dans ces groupes réduit • Taille des groupes centraux augmentée – puisque le temps de "saut" est à peu près indépendant de la taille du groupe • Autre approche : ajouter un second niveau pour permettre le saut de deux ou plusieurs groupes en une étape (plus de 2 niveaux possible) • Algorithmes existants pour déterminer les taille de groupes optimales pour différentes technologies et implantations (càd différentes valeurs du ratio (ts+tb)/tr) 21

Groupes de taille variable • A l'inverse du cas des groupes constants – on ne peut se restreindre à l'analyse du pire cas de la propagation de la retenue • Peut mener à la conclusion triviale : le premier et le dernier groupe composé d'un seul étage (1 bit) – les n-2 étages restants constituant un seul groupe central • La retenue générée au début du groupe central peut se propager à travers les autre n-3 étages – et par là devenant le pire cas • On doit donc considérer toutes les chaînes de retenue démarrant à n'importe quelle position arbitraire de bit a (avec xa=ya) et s'arrêtant à b (xb=yb), position à laquelle une nouvelle chaîne de retenue (indépendante de la précédente) commence. (X et Y opérandes) 22

Optimiser les taille de groupe • k 1, k 2, … , k. L – tailles des L groupes – avec • Cas général : Chaîne commençant dans le groupe u, finissant dans le groupe v, sautant les groupes u+1, u+2, … , v-1 • Pire cas - retenue générée à la première position dans u et finissant dans la dernière position dans v • Le temps de propagation de la retenue est : • Nombre de groupes L et tailles k 1, k 2, …, k. L sélectionnées de telle façon que la plus longue chaîne de propagation de la retenue soit minimale • Solutions algorithmiques développées - programmation dynamique 23

Optimisation - Exemple • additionneur 32 -bit avec un seul niveau de saut • ts+tb=tr • Organisation optimale - L=10 groupes de taille k 1, k 2, …, k 10 = 1, 2, 3, 4, 5, 6, 5, 3, 2, 1 • Résultat Tcarry 9 tr • Si tr=2 G - Tcarry 18 G au lieu 25 G pour des groupes de taille égale • Exercice: Montrer que toute paire de position de bits dans deux groupes quelconques u et v ( 1 u v 10 ) satisfait Tcarry(u, v) 9 tr 24

IV- Additionneur à retenue anticipée (Carry Look-Ahead : CLA) • L'inconvénient des structures précédentes est le temps nécessaire à la réalisation de l'addition. Ce temps est en effet conditionné par la propagation de la retenue à travers tous les additionneurs élémentaires. • Dans un additionneur à retenue anticipée on évalue en même temps la retenue de chaque étage. Pour cela on détermine pour chaque étage les quantités Pi et Gi suivantes: – pi = ai bi (propagation d'une retenue) – gi = ai. bi (génération d'une retenue) 25

Additionneur à retenue anticipée : CLA pi= ai bi gi = ai. bi (propagation d'une retenue) (génération d'une retenue) La retenue entrante à l'ordre i vaut 1 si : - soit l'étage i-1 a généré la retenue (gi-1 = 1) - soit l'étage i-1 a propagé la retenue générée à l'étage i-2 (pi-1=1 et gi-2=1) - soit les étages i-1 et i-2 ont propagé la retenue générée à l'étage i-3 (pi-1=pi-2=1 et gi-3=1). . - soit tous les étages inférieurs ont propagé la retenue entrante dans l'additionneur (pi-1=pi-2=. . . =p 0=c 0=1). ci = gi-1 + pi-1. gi-2 + pi-1. pi-2. gi-3 +. . . . + pi-1. pi-2. pi-3. . p 0. c 0 c 1 = g 0 + p 0. c 0 c 2 = g 1 + p 1. g 0 + p 1. p 0. c 0 c 3 = g 2 + p 2. g 1 + p 2. p 1. g 0 + p 2. p 1. p 0. c 0 c 4 = g 3 + p 3. g 2 + p 3. p 2. g 1 + p 3. p 2. p 1. g 0 + p 3. p 2. p 1. p 0. c 0 26

Additionneur à retenue anticipée pi= ai bi (propagation d'une retenue) gi = ai. bi (génération d'une retenue) Si = ai bi ci = pi ci ci = gi-1 + pi-1. gi-2 + pi-1. pi-2. gi-3 +. . . . + pi-1. pi-2. pi-3. . p 0. c 0 27

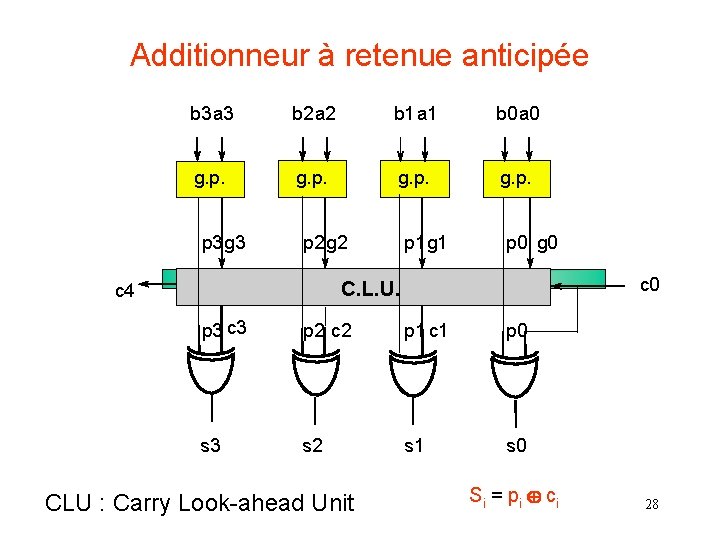
Additionneur à retenue anticipée b 3 a 3 b 2 a 2 b 1 a 1 b 0 a 0 g. p. p 3 g 3 p 2 g 2 p 1 g 1 p 0 g 0 c 0 C. L. U. c 4 p 3 c 3 p 2 c 2 p 1 c 1 p 0 s 3 s 2 s 1 s 0 CLU : Carry Look-ahead Unit Si = pi ci 28

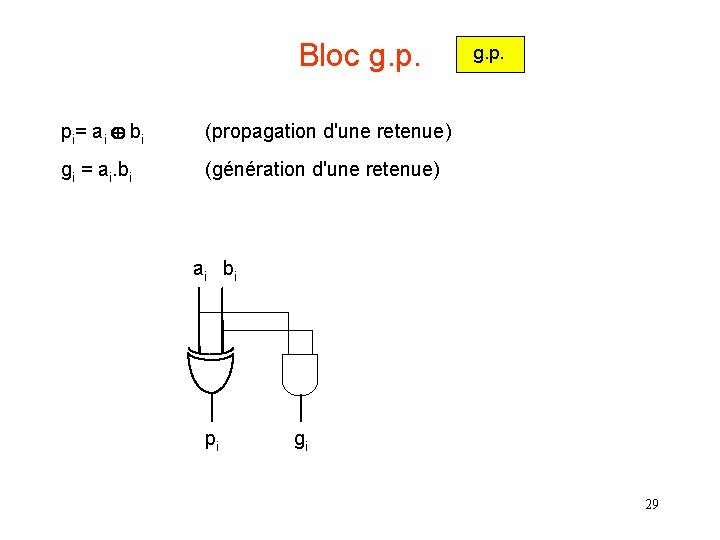
Bloc g. p. pi= ai bi (propagation d'une retenue) gi = ai. bi (génération d'une retenue) g. p. ai bi pi gi 29

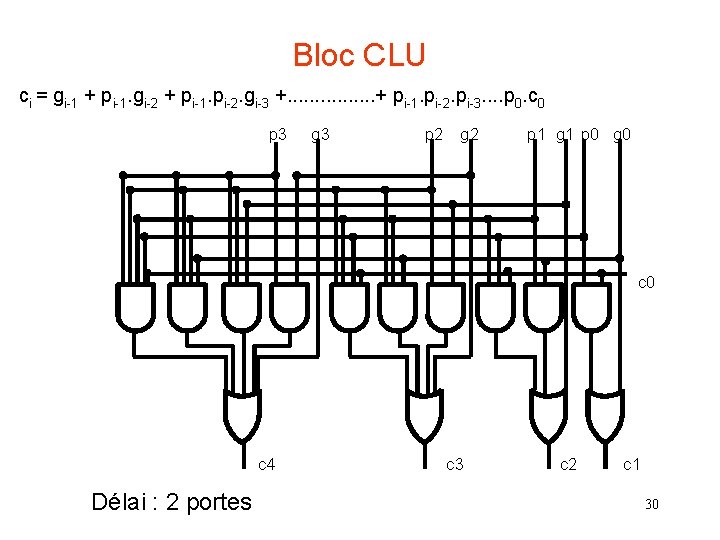
Bloc CLU ci = gi-1 + pi-1. gi-2 + pi-1. pi-2. gi-3 +. . . . + pi-1. pi-2. pi-3. . p 0. c 0 p 3 g 3 p 2 g 2 p 1 g 1 p 0 g 0 c 4 Délai : 2 portes c 3 c 2 c 1 30

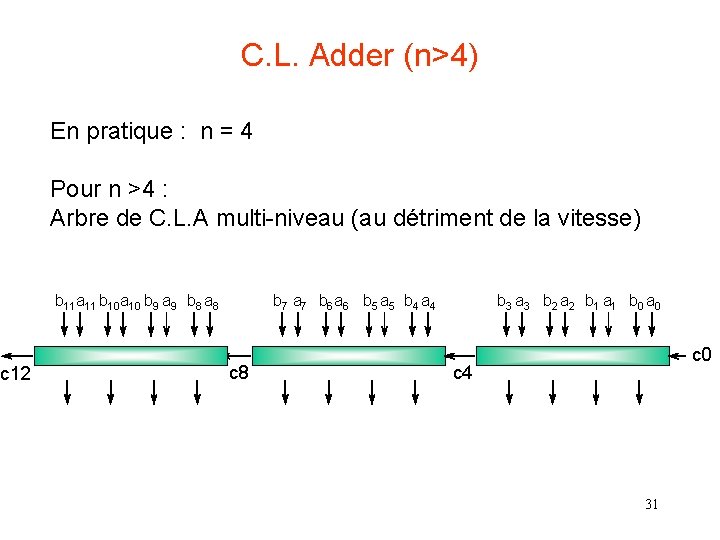
c 12 C. L. Adder (n>4) En pratique : n = 4 Pour n >4 : Arbre de C. L. A multi-niveau (au détriment de la vitesse) b 11 a 11 b 10 a 10 b 9 a 9 b 8 a 8 b 7 a 7 b 6 a 6 b 5 a 5 b 4 a 4 c 8 b 3 a 3 b 2 a 2 b 1 a 1 b 0 a 0 c 4 31

V- Génération et propagation de groupe Soient gi , pi , Pi, j , Gi, j définis de la façon suivante : Gi, i = gi = ai. bi : génération au rang i Pi, i = pi = ai bi : propagation au rang i Gi, k = Gi, j + Pi, j. Gj-1, k : génération du rang k au rang i (n>i≥j≥k≥ 0) Pi, k = Pi, j. Pj-1, k : propagation du rang k au rang i Gi, k : la retenue qui sort de l'étage i a été générée entre l'étage k et l'étage i Pi, k : le retenue entrant à l'étage k a été propagée jusqu'à la sortie de l'étage i ci+1 = Gi, 0 + Pi, 0. c 0 : retenue au rang i+1 que l'on cherche à obtenir Si = ai bi ci = pi (Gi-1, 0 + Pi-1, 0. c 0) et S 0 =p 0 c 0 32

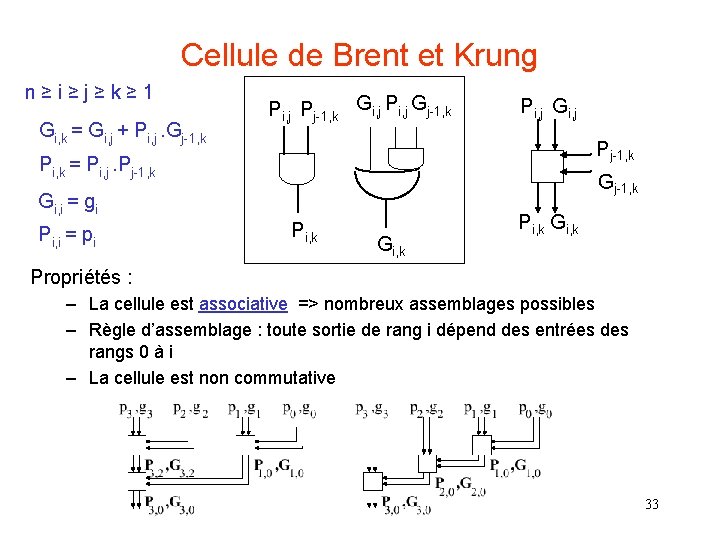
Cellule de Brent et Krung n ≥ i ≥ j ≥ k ≥ 1 Gi, k = Gi, j + Pi, j. Gj-1, k Pi, j Pj-1, k Gi, j Pi, j Gj-1, k Pi, j Gi, j Pj-1, k Pi, k = Pi, j. Pj-1, k Gi, i = gi Pi, i = pi Pi, k Gi, k Propriétés : – La cellule est associative => nombreux assemblages possibles – Règle d’assemblage : toute sortie de rang i dépend des entrées des rangs 0 à i – La cellule est non commutative 33

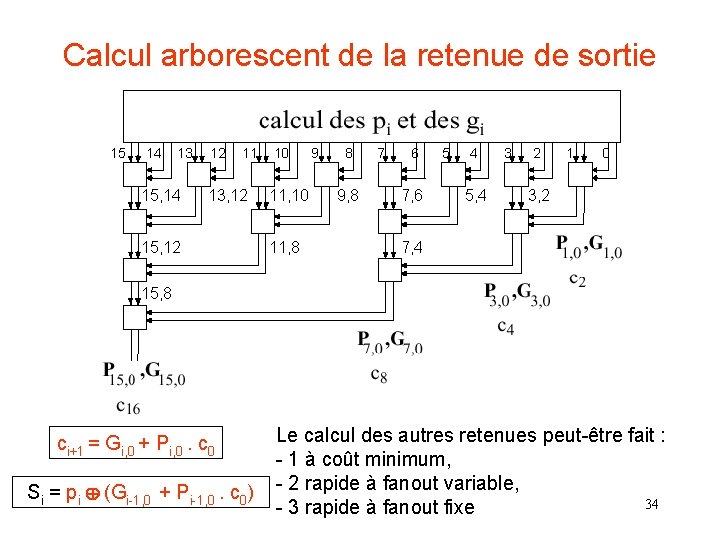
Calcul arborescent de la retenue de sortie 15 14 13 15, 14 12 11 13, 12 15, 12 10 11, 8 9, 8 7 6 7, 6 5 4 5, 4 3 2 1 0 3, 2 7, 4 15, 8 ci+1 = Gi, 0 + Pi, 0. c 0 Si = pi (Gi-1, 0 + Pi-1, 0. c 0) Le calcul des autres retenues peut-être fait : - 1 à coût minimum, - 2 rapide à fanout variable, 34 - 3 rapide à fanout fixe

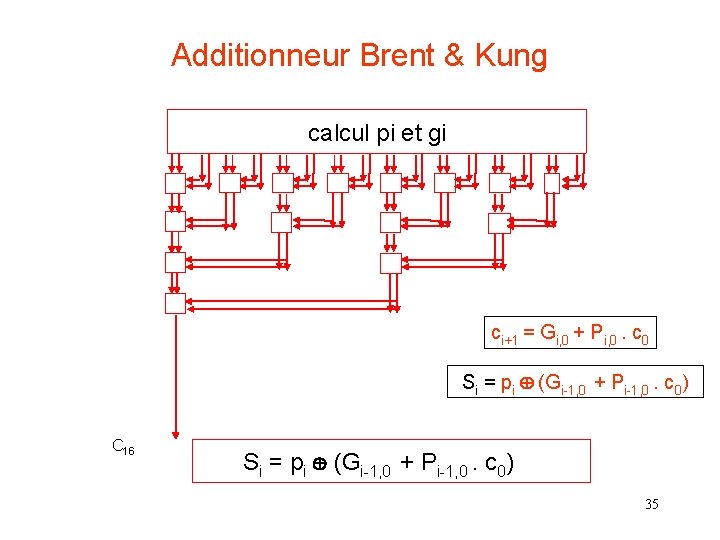
Additionneur Brent & Kung calcul pi et gi ci+1 = Gi, 0 + Pi, 0. c 0 Si = pi (Gi-1, 0 + Pi-1, 0. c 0) C 16 Si = pi (Gi-1, 0 + Pi-1, 0. c 0) 35

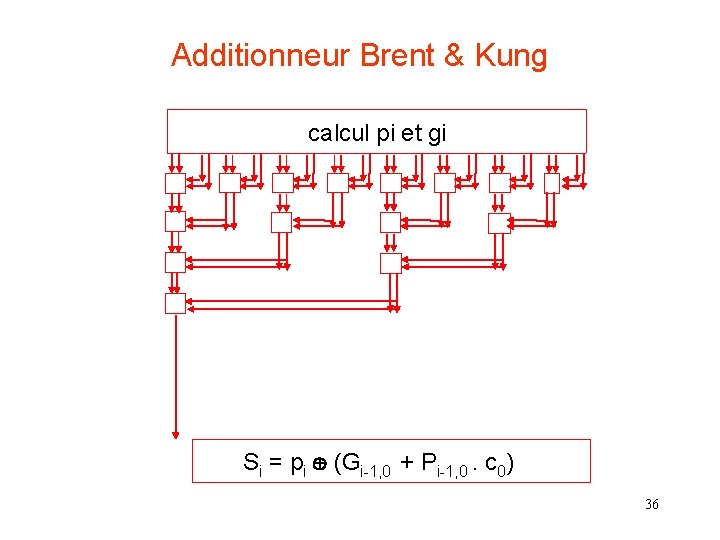
Additionneur Brent & Kung calcul pi et gi Si = pi (Gi-1, 0 + Pi-1, 0. c 0) 36

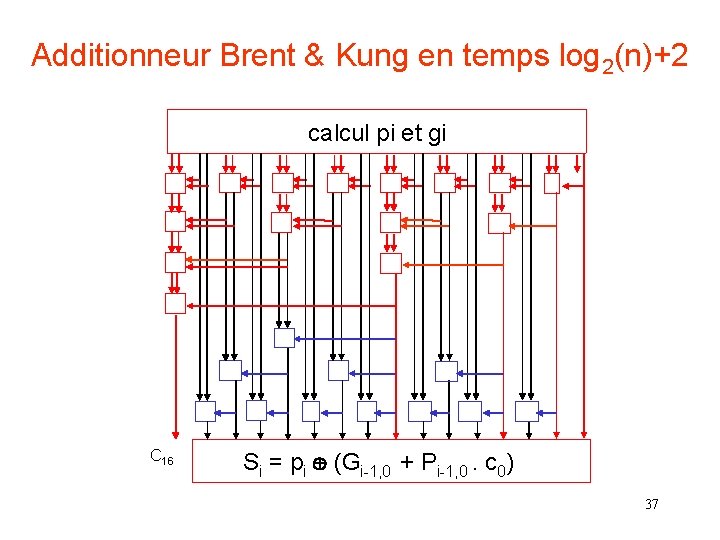
Additionneur Brent & Kung en temps log 2(n)+2 calcul pi et gi C 16 Si = pi (Gi-1, 0 + Pi-1, 0. c 0) 37

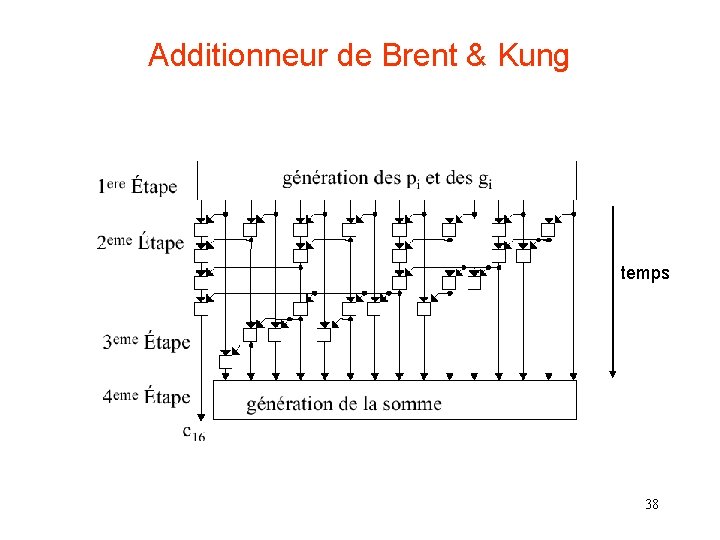
Additionneur de Brent & Kung temps 38

Règles de construction Il y a une seule règle de construction des arbres imbriqués de cellules "BK" : Toute retenue ci de rang i est reliée à toutes les entrées de rang j < i par un arbre binaire planaire de cellules "BK". Cela permet d'entrelacer les arbres des n sorties de très nombreuses façons en fonction du nombre de bits et du délai de l'additionneur. Ce délai va de (n-1) à log 2(n), bornes comprises. 39

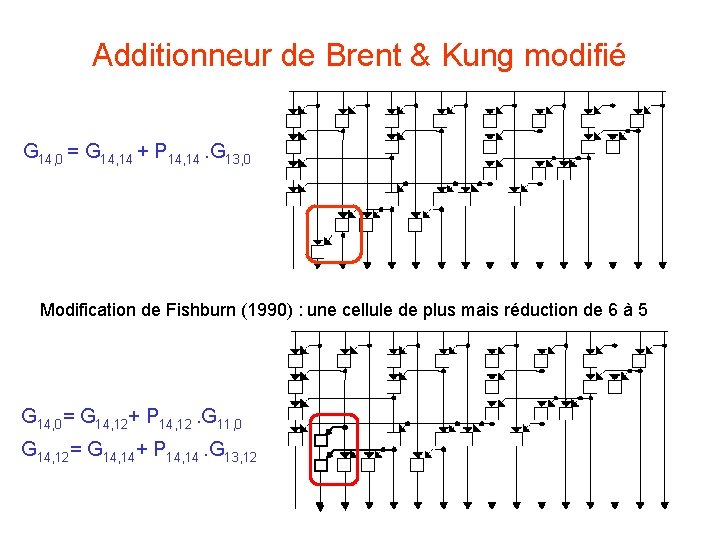
Additionneur de Brent & Kung modifié G 14, 0 = G 14, 14 + P 14, 14. G 13, 0 Modification de Fishburn (1990) : une cellule de plus mais réduction de 6 à 5 G 14, 0= G 14, 12+ P 14, 12. G 11, 0 G 14, 12= G 14, 14+ P 14, 14. G 13, 12 40

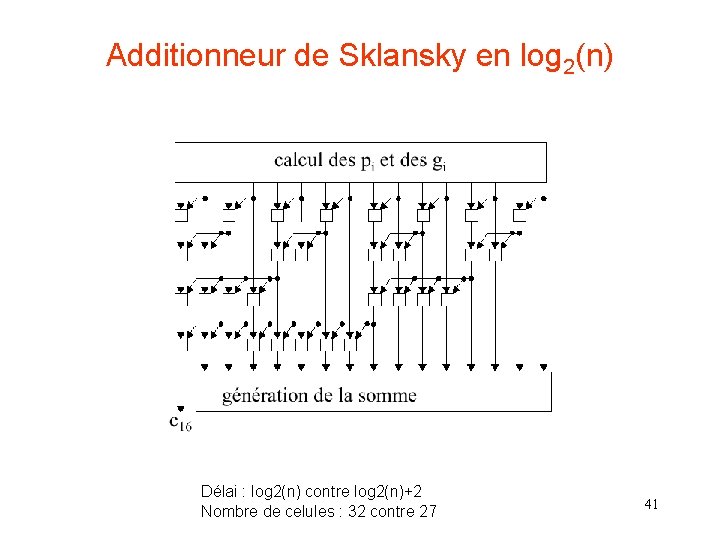
Additionneur de Sklansky en log 2(n) Délai : log 2(n) contre log 2(n)+2 Nombre de celules : 32 contre 27 41

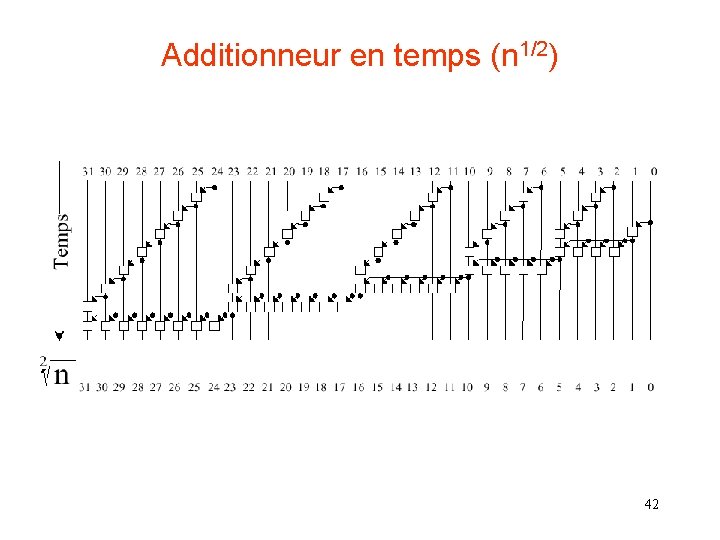
Additionneur en temps (n 1/2) 42

Additionneur en temps (n 1/3) 43

Exercice 44

Additionneur de Ling (1981) ki = le retenue a été tuée au rang i = ai'. bi' Calcul de la 6 ième retenue S 6 = p 6 G 5, 0 = G 5, 3 + P 5, 3 G 2, 0 Remarque : gi = k'i gi G 5, 3 = g 5 + k'5 g 4 + k'5 k'4 g 3 G 2, 0 = g 2 + k'2 g 1 + k'2 k'1 g 0 P 5, 3 = k'5 k'4 k'3 Le délai de S 6 est déterminé par G 5, 0 dont tous les termes contiennent k'5 sauf le premier. Or g 5 = k'5 g 5. On met k'5 en facteur : S 6 = p 6 k'5 H 5, 0 (Hi, 0 pseudo-retenue au rang i) H 5, 0 = H 5, 3 + Q 5, 3 H 2, 0 H 5, 3 = g 5 + g 4 + k'4 g 3 H 2, 0 = g 2 + g 1 + k'1 g 0 Q 5, 3 = k'4 k'3 k'2 45

Additionneur de Ling Pour S 6 on précalcule p 6 et p 6 k'5 G 5, 3 = g 5 + k'5 g 4 + k'5 k'4 g 3 = a 5 b 5 + (a 5+b 5)a 4 b 4 + (a 5+b 5) (a 4+b 4)a 3 b 3 H 5, 3 = g 5 + g 4 + k'4 g 3 = a 5 b 5 + a 4 b 4 + (a 4+b 4)a 3 b 3 H 5, 3 est plus rapide à calculer que G 5, 3 46

Additionneurs Parallèles • • • But : éviter la propagation de la retenue Astuce : coder les chiffres sur 2 bits Le résultat est la somme de l'addition et de la retenue de l'étage précédent • codage : 00, 1 : 01 ou 10, 2 : 11 • (13)10= 1*23+1*22+0*21+1*20 = >1101 en binaire naturel => 01 01 00 01 en CS ou bien = 1*23+0*22+2*21+1*20 = > 01 00 11 01 en CS 47

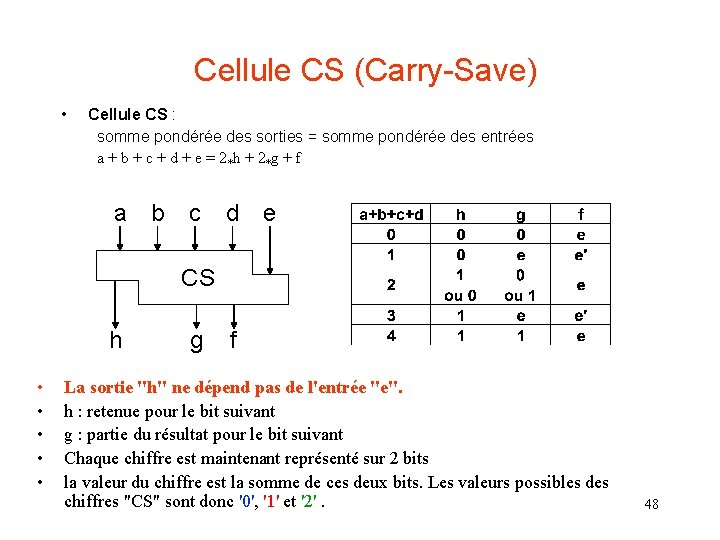
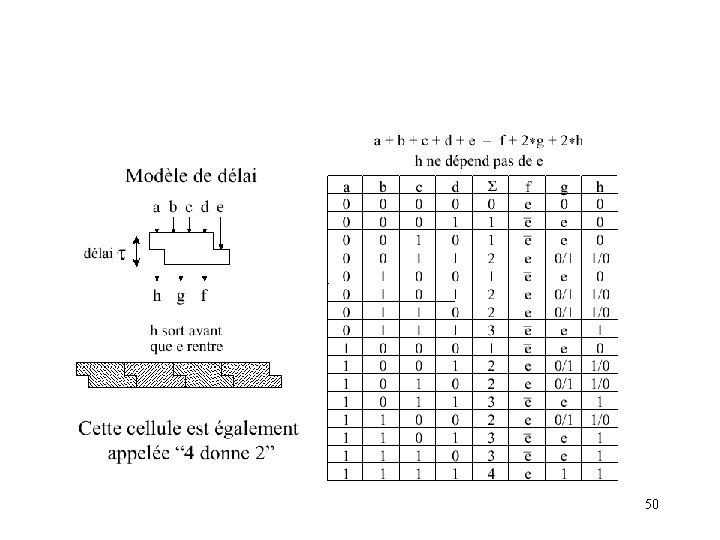
Cellule CS (Carry-Save) • Cellule CS : somme pondérée des sorties = somme pondérée des entrées a + b + c + d + e = 2*h + 2*g + f a b c d e CS h • • • g f La sortie "h" ne dépend pas de l'entrée "e". h : retenue pour le bit suivant g : partie du résultat pour le bit suivant Chaque chiffre est maintenant représenté sur 2 bits la valeur du chiffre est la somme de ces deux bits. Les valeurs possibles des chiffres "CS" sont donc '0', '1' et '2'. 48

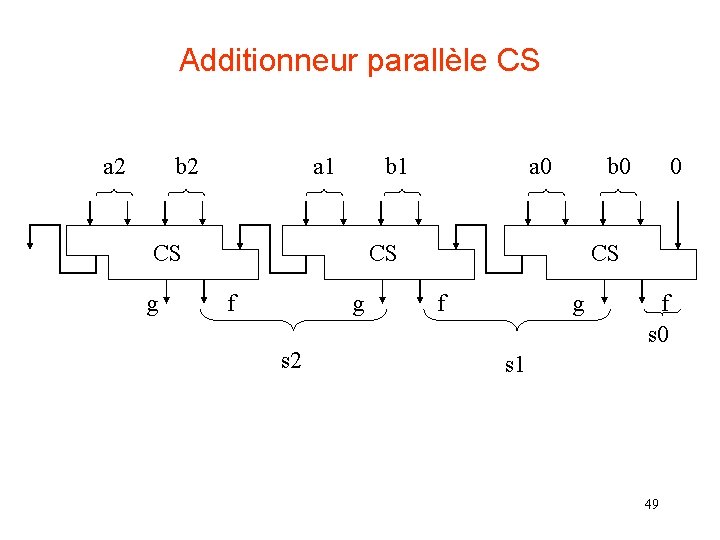
Additionneur parallèle CS a 2 b 2 a 1 b 1 CS g a 0 b 0 CS f g s 2 0 CS f g f s 0 s 1 49

50

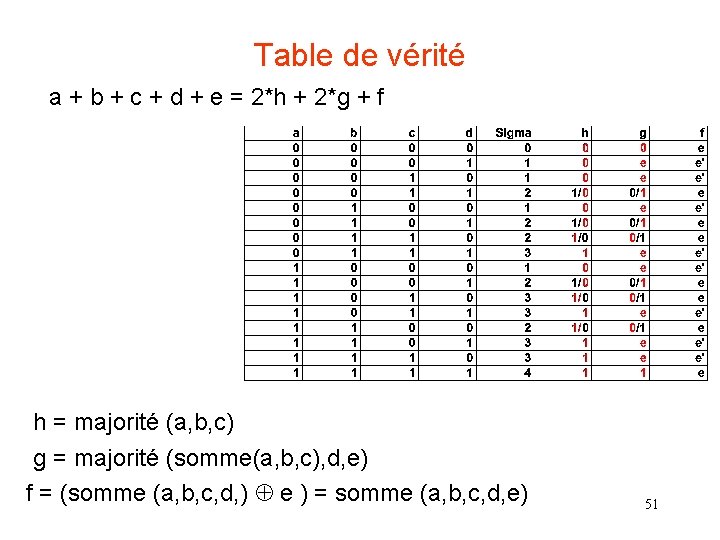
Table de vérité a + b + c + d + e = 2*h + 2*g + f h = majorité (a, b, c) g = majorité (somme(a, b, c), d, e) f = (somme (a, b, c, d, ) e ) = somme (a, b, c, d, e) 51

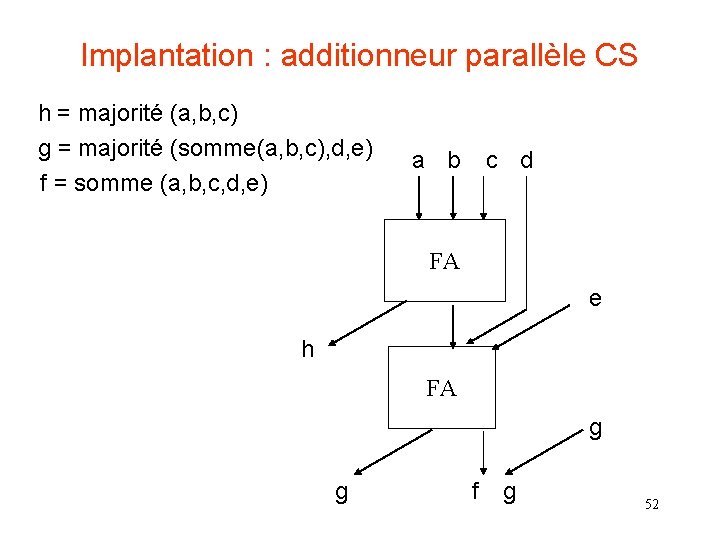
Implantation : additionneur parallèle CS h = majorité (a, b, c) g = majorité (somme(a, b, c), d, e) f = somme (a, b, c, d, e) a b c d FA e h FA g g f g 52

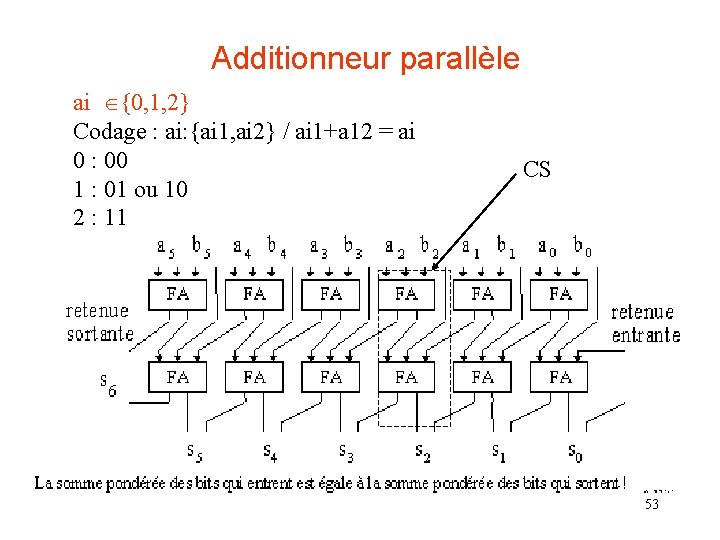
Additionneur parallèle ai {0, 1, 2} Codage : ai: {ai 1, ai 2} / ai 1+a 12 = ai 0 : 00 1 : 01 ou 10 2 : 11 CS 53

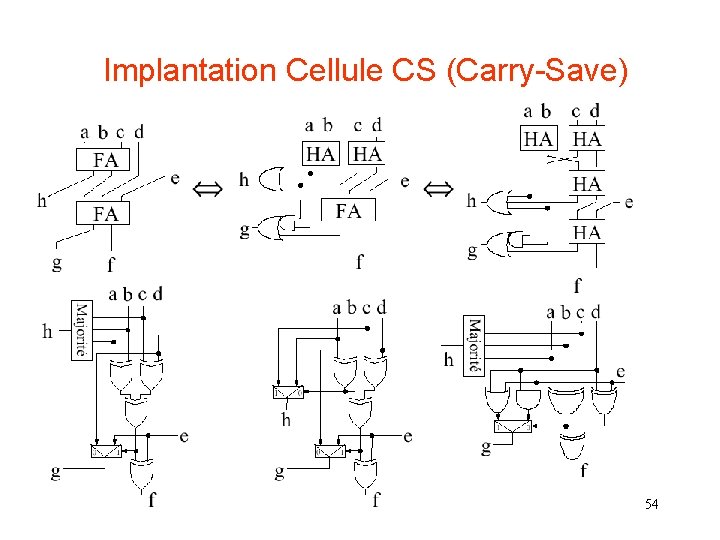
Implantation Cellule CS (Carry-Save) 54

Variantes 55

Additionneurs de réels 56

Nombre réels • Codage des réels : virgule flottante • flottant stocké sous la forme M * BE – M : Mantisse ; B : Base ; E : Exposant • exemple : 123. 103 = 123 000 • Représentation IEEE 754, base 2 (signe 1 bit, exposant et mantisse sur 32 ou 64 bits pour simple et double précision) • SM : signe de la mantisse : 1 bit • Eb : exposant biaisé : 8 ou 11 bits • M : Mantisse : 23 ou 52 bits SM Eb M 57

Mantisse et exposant • • Signe : bit de poids fort (0 = + ; 1 = -) Exposant – placé avant la mantisse pour simplifier les comparaisons (pour ceci il ne doit pas être représenté en complément à deux : 2 -1 > 2) – sur 8 bits : 0. . 255 – sans signe mais biaisé de 127 (on enlève 127) : – Eb = 0 ⇒ E = 0 – 127 = -127 – Eb = 255 ⇒ E = 255 – 127 = 128 • Remarque : E>0 si et seulement si le bit de poids fort de Eb =1 • Mantisse – normalisée : bit de poids fort n’est pas 0 et un seul chiffre avant la virgule • ex : 3, 2510 =11, 01 = 1, 101 * 21 58

Virgule Flottante • Mantisse : Comme le bit de poids fort de la mantisse est nécessairement 1, on ne l’indique pas (gaspillage de place). Il est implicite – partie fractionnaire = f 1 f 2 …fn ⇒ m = 1, f 1 f 2…fn – nombre x = (-1)SM * 1, M * 2 Eb-127 • Exemple – – x = (-2, 5)10 = (-1, 01*21)2 SM = 1 ; E= 1 => Eb= 128 = 1000 0000 ; m=1, 01 => M = 010……. 0 1 1000 010…… 0 59

Exemple : 452, 5 + 117, 5 452, 5= A=1. 1100010010000000*28 117, 5= B=1. 110101100000000*26 452, 5= A=1. 1100010010000000*28 117, 5= B=0. 01110101100000000*28 A+B = 10. 0011101000000000*28 = 1. 00011101000000000*29 60

Addition virgule flottante • Les réels étant codés en "signe/valeur absolue", un seul opérateur pour addition et soustraction (Cmp à 1 +1 si signes dif. ) • Exposant du résultat : exposant du + grand (voir la suite) • Déroulement de l'addition – alignement des mantisses si les exposants sont dif. – addition ou soustraction des mantisses alignées – renormalisation de la mantisse de la somme S (si elle n'est pas normalisée) => modif de l'exposant – arrondi de la mantisse 61

Exemple : 452, 5+117, 5 452, 5= A=1. 1100010010000000*28 117, 5= B=1. 110101100000000*26 Alignement des mantisses B= 0. 0111010110000000|00*28 Addition des mantisses alignées A=1. 110001001000000000*28 +B=0. 011101011000000000*28 S=10. 00111010000000000*28 Normalisation de la mantisse S'=1. 000111010000000000*29 Arrondi de la mantisse S'=1. 0001110100000000*29 62

Alignement des mantisses • Par décalage de p bits • La valeur p du décalage est donnée par la différence des exposants. Dans l'exemple 8 -6 =2. Décalage de 2 bits. • La valeur max de décalage est 23 , la différence est codée sur 5 bits 63

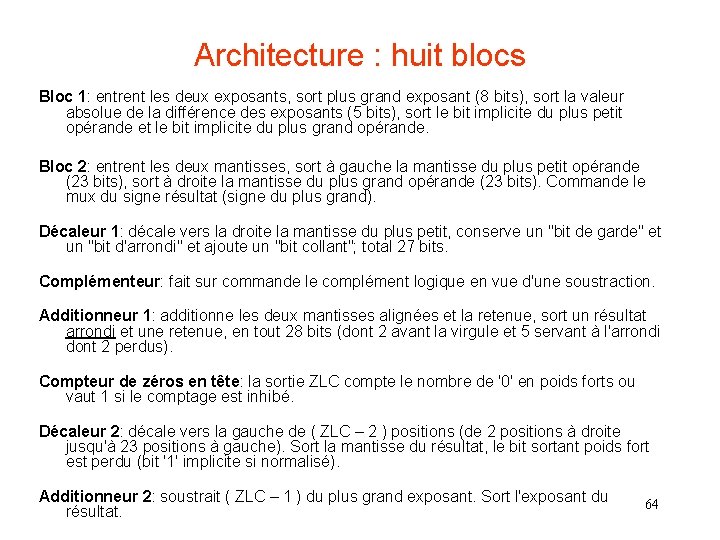
Architecture : huit blocs Bloc 1: entrent les deux exposants, sort plus grand exposant (8 bits), sort la valeur absolue de la différence des exposants (5 bits), sort le bit implicite du plus petit opérande et le bit implicite du plus grand opérande. Bloc 2: entrent les deux mantisses, sort à gauche la mantisse du plus petit opérande (23 bits), sort à droite la mantisse du plus grand opérande (23 bits). Commande le mux du signe résultat (signe du plus grand). Décaleur 1: décale vers la droite la mantisse du plus petit, conserve un "bit de garde" et un "bit d'arrondi" et ajoute un "bit collant"; total 27 bits. Complémenteur: fait sur commande le complément logique en vue d'une soustraction. Additionneur 1: additionne les deux mantisses alignées et la retenue, sort un résultat arrondi et une retenue, en tout 28 bits (dont 2 avant la virgule et 5 servant à l'arrondi dont 2 perdus). Compteur de zéros en tête: la sortie ZLC compte le nombre de '0' en poids forts ou vaut 1 si le comptage est inhibé. Décaleur 2: décale vers la gauche de ( ZLC – 2 ) positions (de 2 positions à droite jusqu'à 23 positions à gauche). Sort la mantisse du résultat, le bit sortant poids fort est perdu (bit '1' implicite si normalisé). Additionneur 2: soustrait ( ZLC – 1 ) du plus grand exposant. Sort l'exposant du résultat. 64

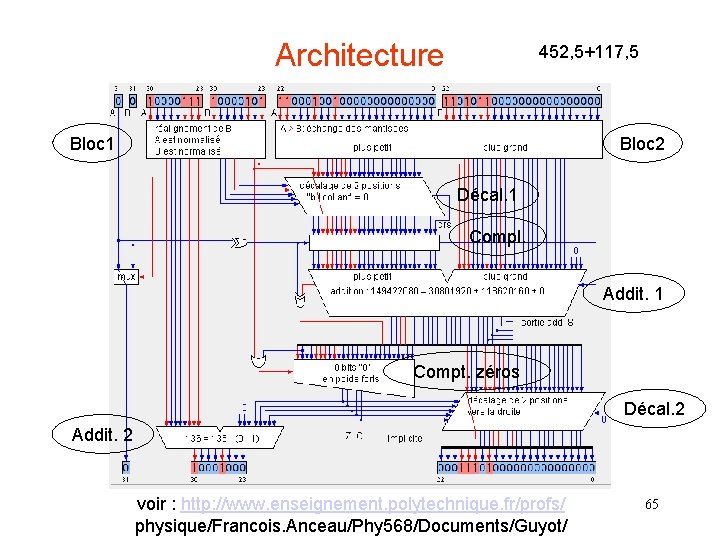
Architecture 452, 5+117, 5 Bloc 1 Bloc 2 Décal. 1 Compl. Addit. 1 Compt. zéros Décal. 2 Addit. 2 voir : http: //www. enseignement. polytechnique. fr/profs/ physique/Francois. Anceau/Phy 568/Documents/Guyot/ 65

Multiplieurs 66

Multiplication binaire 1 1 0 0 Multiplicande 1 2 * 1 3 1 1 0 1 Multiplieur ----- 3 6 1 1 0 0 Produit partiel 1 2 0 0 Produit partiel ---- 1 1 0 0 1 5 6 1 1 0 0 Produit partiel ---------- 1 0 0 1 1 1 0 0 67

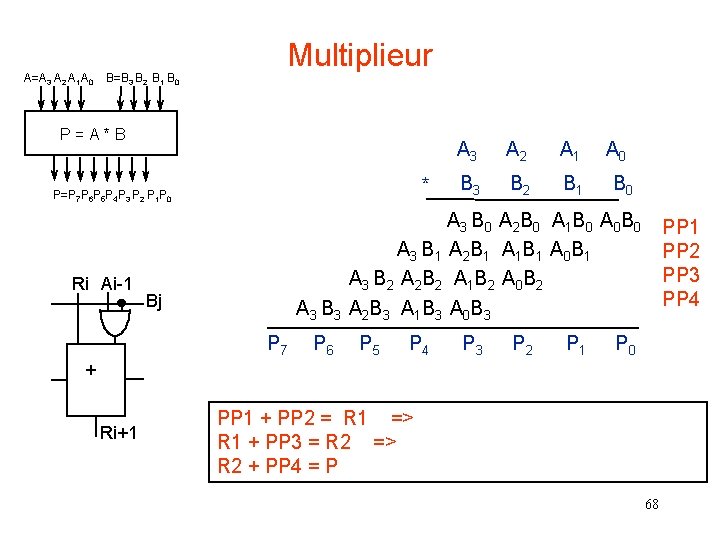
A=A 3 A 2 A 1 A 0 B=B 3 B 2 B 1 B 0 Multiplieur P = A * B A 3 A 2 A 1 A 0 P=P 7 P 6 P 5 P 4 P 3 P 2 P 1 P 0 Ri Ai-1 Bj * B 3 B 2 B 1 B 0 A 3 B 0 A 2 B 0 A 1 B 0 A 0 B 0 A 3 B 1 A 2 B 1 A 1 B 1 A 0 B 1 A 3 B 2 A 2 B 2 A 1 B 2 A 0 B 2 A 3 B 3 A 2 B 3 A 1 B 3 A 0 B 3 PP 1 PP 2 PP 3 PP 4 P 7 P 6 P 5 P 4 P 3 P 2 P 1 P 0 + Ri+1 PP 1 + PP 2 = R 1 => R 1 + PP 3 = R 2 => R 2 + PP 4 = P 68

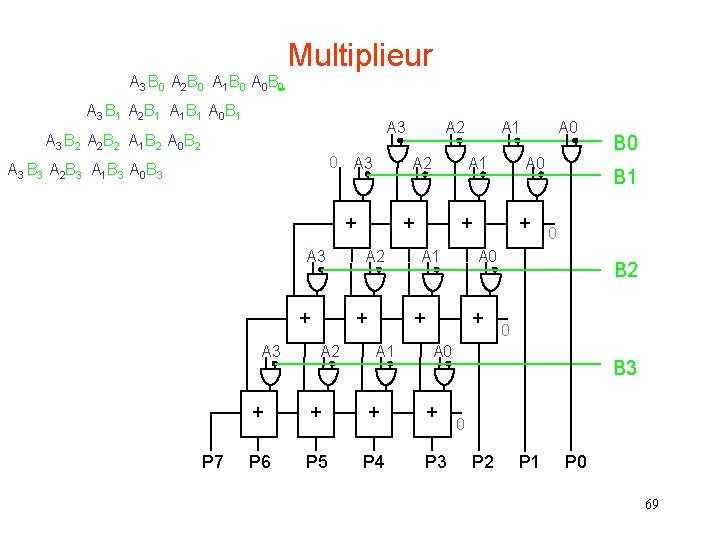
Multiplieur A 3 B 0 A 2 B 0 A 1 B 0 A 0 B 0 A 3 B 1 A 2 B 1 A 1 B 1 A 0 B 1 A 3 B 2 A 2 B 2 A 1 B 2 A 0 B 2 0 A 3 B 3 A 2 B 3 A 1 B 3 A 0 B 3 A 2 + A 3 + A 2 + A 1 + A 0 + + + 0 B 2 0 A 0 + B 0 B 1 A 0 + A 1 A 1 + + A 2 B 3 0 P 7 P 6 P 5 P 4 P 3 P 2 P 1 P 0 69

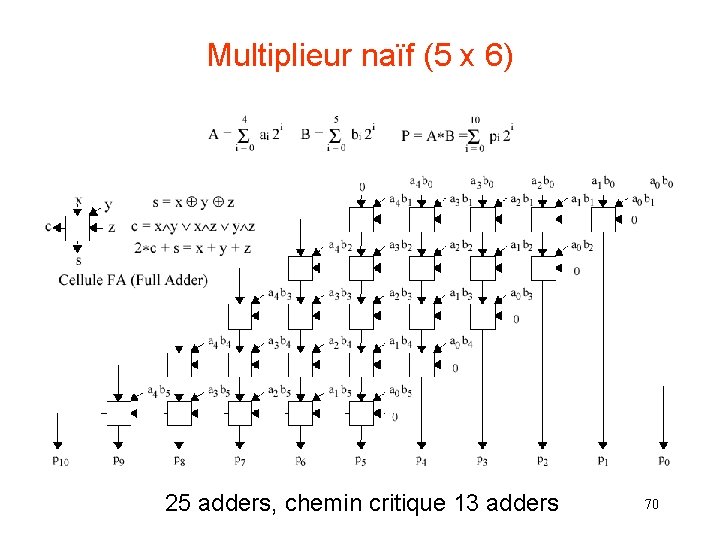
Multiplieur naïf (5 x 6) 25 adders, chemin critique 13 adders 70

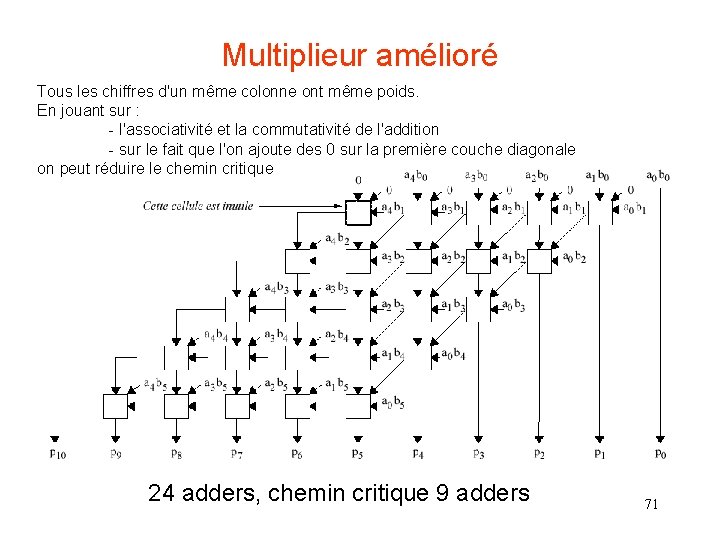
Multiplieur amélioré Tous les chiffres d'un même colonne ont même poids. En jouant sur : - l'associativité et la commutativité de l'addition - sur le fait que l'on ajoute des 0 sur la première couche diagonale on peut réduire le chemin critique 24 adders, chemin critique 9 adders 71

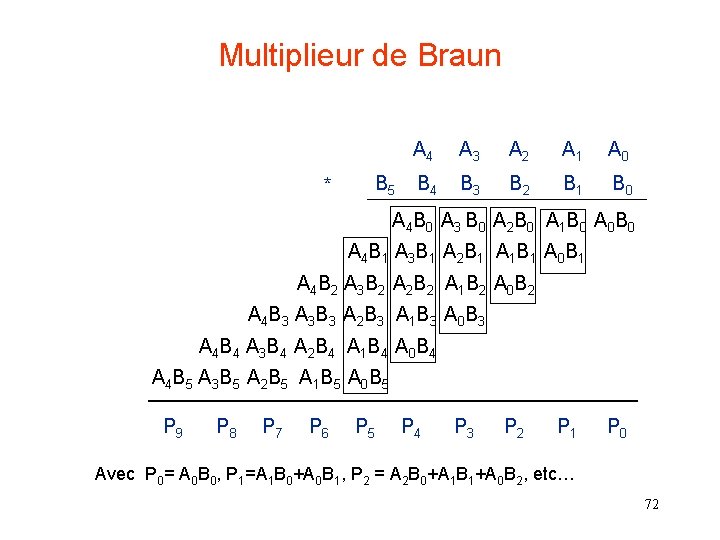
Multiplieur de Braun A 4 A 3 A 2 A 1 A 0 * B 5 B 4 B 3 B 2 B 1 B 0 A 4 B 0 A 3 B 0 A 2 B 0 A 1 B 0 A 0 B 0 A 4 B 1 A 3 B 1 A 2 B 1 A 1 B 1 A 0 B 1 A 4 B 2 A 3 B 2 A 2 B 2 A 1 B 2 A 0 B 2 A 4 B 3 A 3 B 3 A 2 B 3 A 1 B 3 A 0 B 3 A 4 B 4 A 3 B 4 A 2 B 4 A 1 B 4 A 0 B 4 A 4 B 5 A 3 B 5 A 2 B 5 A 1 B 5 A 0 B 5 P 9 P 8 P 7 P 6 P 5 P 4 P 3 P 2 P 1 P 0 Avec P 0= A 0 B 0, P 1=A 1 B 0+A 0 B 1, P 2 = A 2 B 0+A 1 B 1+A 0 B 2, etc… 72

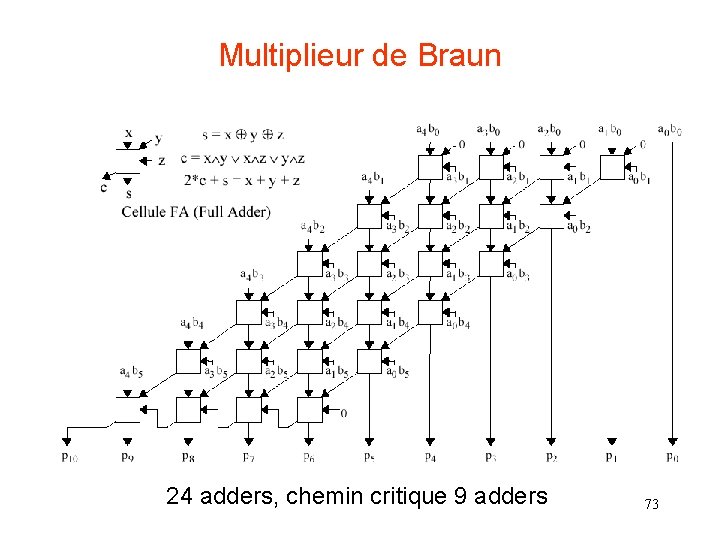
Multiplieur de Braun 24 adders, chemin critique 9 adders 73

Multiplication Signée (complément à 2) 74

Multiplieur séquentiel 1 Avec addition de A sur le ième bit R 2 R 1 +A*20 R 2 R 1 +A*21 R 2 R 1 +0*22 R 2 R 1 +A*23 R 2 R 1 (A) 1110 (B) 1011 ------0000 1110 ------0000 1110 1 110 ------------0010 1010 111 0 ------1001 1010 Initialisation de R 1 et R 2 b 0=1 => on ajoute A*20 Décalage de B => B=(0101) b 0=1 => on ajoute A*21 Décalage de B => B=(0010) b 0=0 => on ajoute 0*22 Décalage de B => B=(0001) b 0=1 => on ajoute A*23 Fin 75

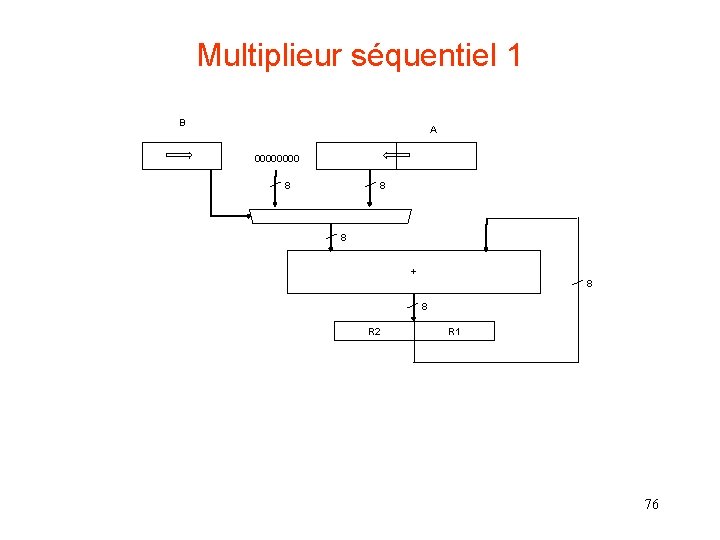
Multiplieur séquentiel 1 B A 0000 8 8 8 + 8 8 R 2 R 1 76

Multiplieur séquentiel 2 Avec addition de A sur les poids forts et décalage (A) (B) R 3 R 2 R 1 +A R 3 R 2 R 1 +0 R 3 R 2 R 1 +A R 3 R 2 R 1 1110 1011 -------0 0000 1110 -------0 1110 0000 0 0111 0000 1110 -------1 0101 0000 0 1010 1000 0000 -------0 1010 1000 0 0101 0100 1110 -------1 0011 0100 0 1001 1010 Initialisation de R 3 R 2 R 1 b 0=1 => (R 2 + A -> R 3 R 2) Décalage de R 3 R 2 R 1 Décalage de B => B=(0101) b 0=1 => (R 2 + A -> R 3 R 2) Décalage de R 3 R 2 R 1 Décalage de B => B=(0010) b 0=0 => (R 2 + 0 -> R 3 R 2) Décalage de R 3 R 2 R 1 Décalage de B => B=(0001) b 0=1 => (R 2 + A -> R 3 R 2) Décalage de R 3 R 2 R 1 Fin A la ième itération : n-i bits à 0 et n-i bits utiles dans B 77

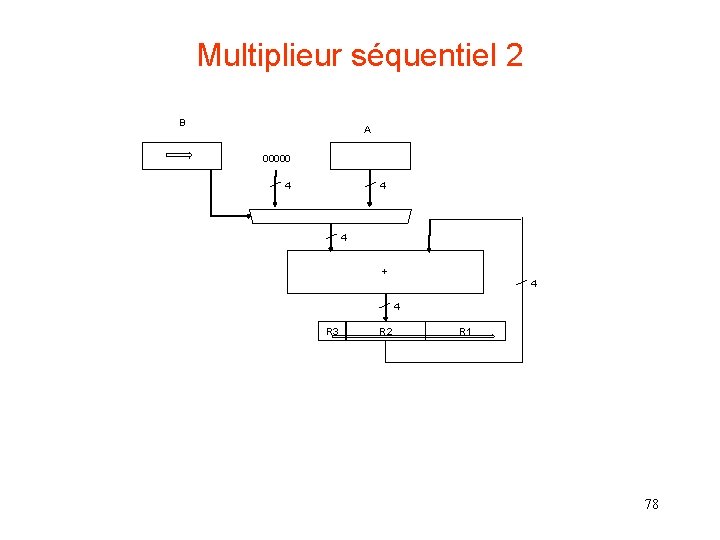
Multiplieur séquentiel 2 B A 00000 4 4 4 + 4 4 R 3 R 2 R 1 78

Multiplieur séquentiel 3 (A) R 3 R 2 R 1 +A R 3 R 2 R 1 +0 R 3 R 2 R 1 +A R 3 R 2 R 1 1110 -------0 0000 1011 1110 -------0 1110 1011 0 0111 0101 1110 -------1 0101 0 1010 0000 -------0 1010 0 0101 1110 -------1 0011 0101 0 1001 1010 Initialisation de R 3 R 2 R 1 (B->R 1) b 0(R 1)=1 => (R 2 + A -> R 3 R 2) Décalage de R 3 R 2 R 1 b 0(R 1)=0 => (R 2 + 0 -> R 3 R 2) Décalage de R 3 R 2 R 1 b 0(R 1)=1 => (R 2 + A -> R 3 R 2) Décalage de R 3 R 2 R 1 Fin 79

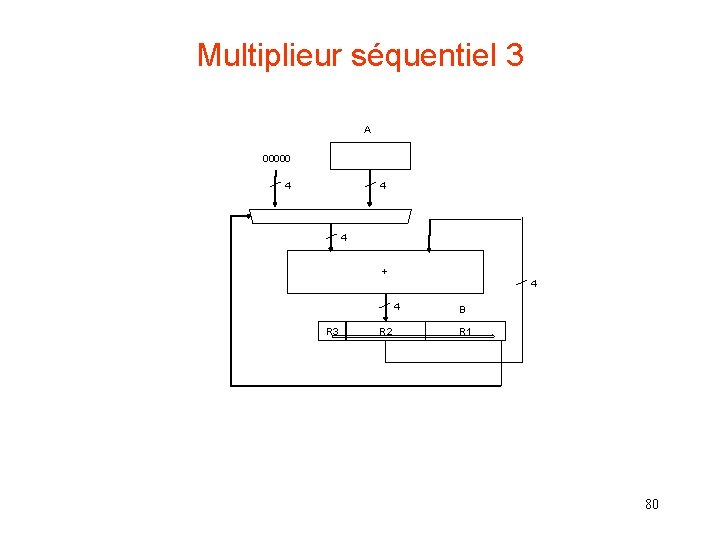
Multiplieur séquentiel 3 A 00000 4 4 4 + 4 4 R 3 R 2 B R 1 80

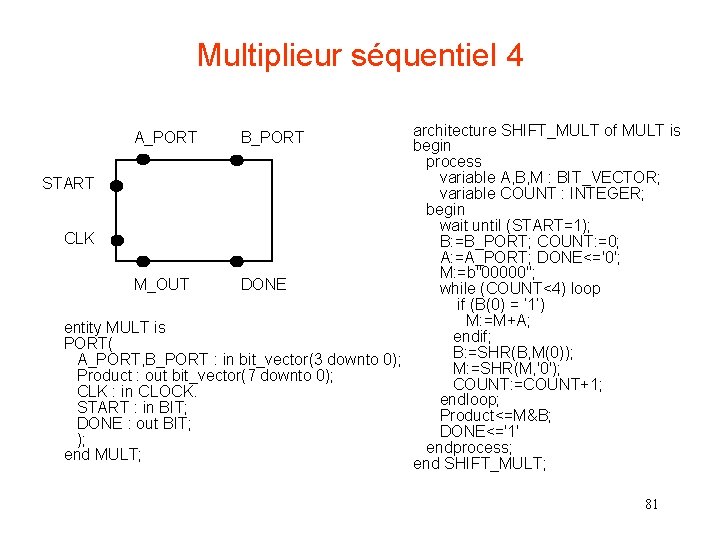
Multiplieur séquentiel 4 architecture SHIFT_MULT of MULT is begin process variable A, B, M : BIT_VECTOR; START variable COUNT : INTEGER; begin wait until (START=1); CLK B: =B_PORT; COUNT: =0; A: =A_PORT; DONE<='0'; M: =b"00000"; M_OUT DONE while (COUNT<4) loop if (B(0) = ‘ 1’) M: =M+A; entity MULT is endif; PORT( A_PORT, B_PORT : in bit_vector(3 downto 0); B: =SHR(B, M(0)); M: =SHR(M, '0'); Product : out bit_vector(7 downto 0); COUNT: =COUNT+1; CLK : in CLOCK. endloop; START : in BIT; Product<=M&B; DONE : out BIT; DONE<='1' ); endprocess; end MULT; end SHIFT_MULT; A_PORT B_PORT 81

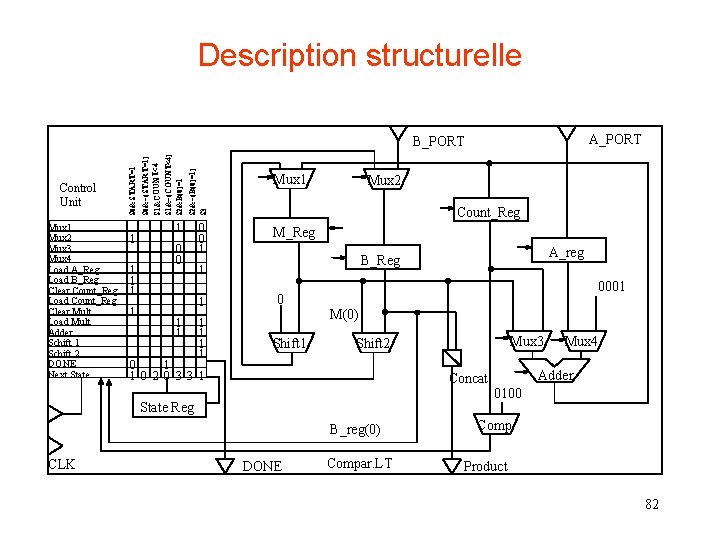
Description structurelle A_PORT Mux 1 Mux 2 Mux 3 Mux 4 Load A_Reg Load B_Reg Clear Count_Reg Load Count_Reg Clear Mult Load Mult Adder Schift 1 Schift 2 DONE Next State 1 1 1 S 2&~(B(0)=1) S 3 S 1&~(COUNT<4) S 2&B(0)=1 S 0&~(START=1) S 1&COUNT<4 Control Unit S 0&START=1 B_PORT 1 0 0 1 Mux 2 Count_Reg M_Reg 1 1 0001 0 M(0) Shift 1 Mux 3 Shift 2 0 1 1 0 2 0 3 3 1 Concat State Reg B_reg(0) CLK A_reg B_Reg 1 1 Mux 1 DONE Compar. LT Mux 4 Adder 0100 Comp Product 82

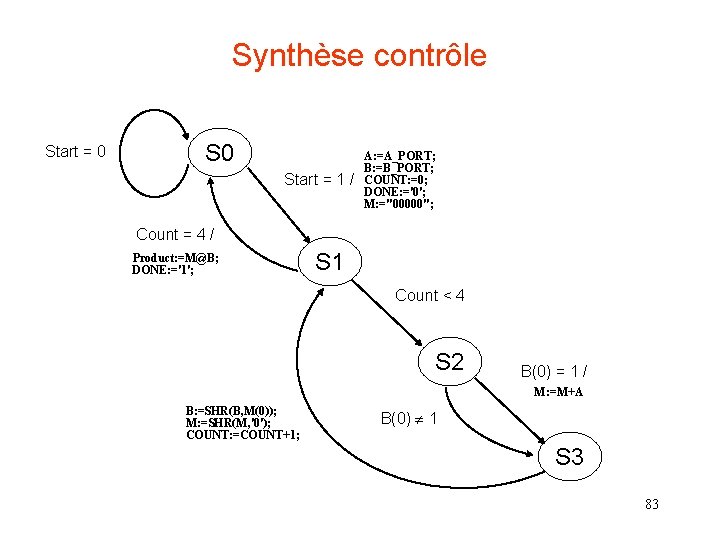
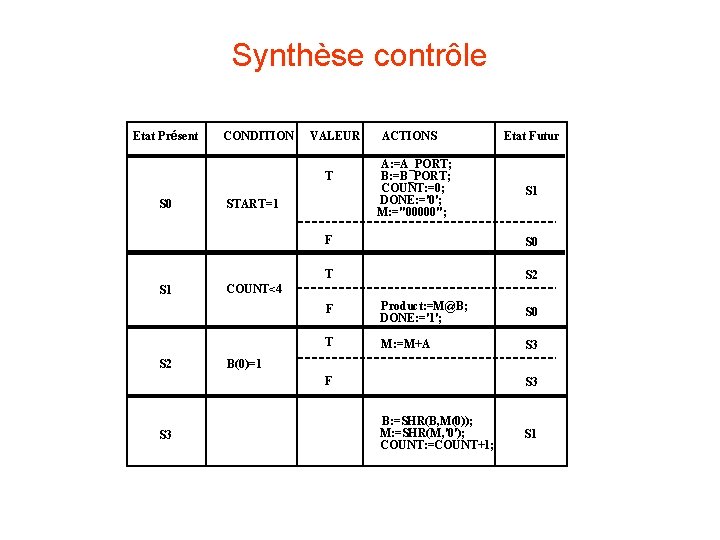
Synthèse contrôle Start = 0 Start = 1 / A: =A_PORT; B: =B_PORT; COUNT: =0; DONE: ='0'; M: ="00000"; Count = 4 / Product: =M@B; DONE: ='1'; S 1 Count < 4 S 2 B(0) = 1 / M: =M+A B: =SHR(B, M(0)); M: =SHR(M, '0'); COUNT: =COUNT+1; B(0) 1 S 3 83

Synthèse contrôle Etat Présent CONDITION VALEUR T S 0 S 1 S 2 START=1 ACTIONS A: =A_PORT; B: =B_PORT; COUNT: =0; DONE: ='0'; M: ="00000"; S 1 F S 0 T S 2 COUNT<4 F Product: =M@B; DONE: ='1'; S 0 T M: =M+A S 3 B(0)=1 F S 3 Etat Futur S 3 B: =SHR(B, M(0)); M: =SHR(M, '0'); COUNT: =COUNT+1; S 1

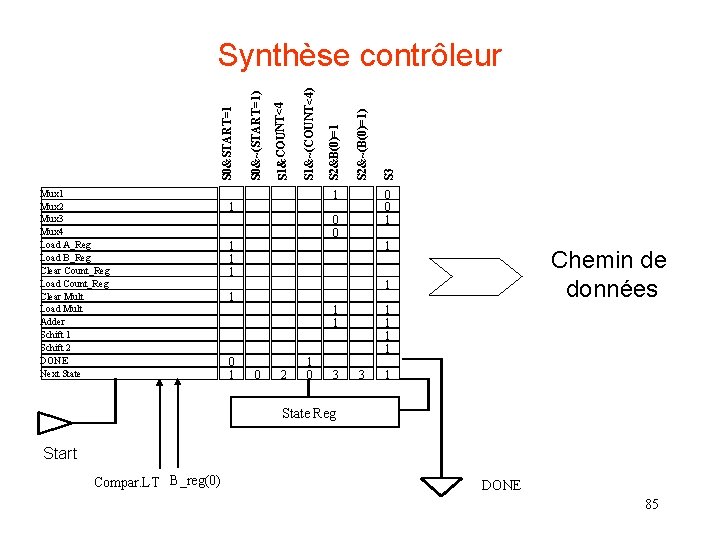
Mux 1 Mux 2 Mux 3 Mux 4 Load A_Reg Load B_Reg Clear Count_Reg Load Count_Reg Clear Mult Load Mult Adder Schift 1 Schift 2 DONE Next State 0 0 1 1 1 S 3 S 2&~(B(0)=1) 1 1 1 Chemin de données 1 1 0 1 S 2&B(0)=1 S 1&~(COUNT<4) S 1&COUNT<4 S 0&~(START=1) S 0&START=1 Synthèse contrôleur 1 1 0 2 1 0 3 1 1 3 1 State Reg Start Compar. LT B_reg(0) DONE 85

Multiplieur de Booth : Principe L'algorithme de Booth est basé sur 2 principes : - une suite de 0's dans B ne demande ni addition ni soustraction (juste un décalage) - une suite de 1's dans B est associée avec une combinaison d'une soustraction (là où la suite commence) et une addition (là où la suite finit). Justification : …. . 0111110…. . = . …. 100000 - 1 Donc : au passage 01 on rajoute A au passage 10 on enlève A 86

Multiplieur de Booth : Implantation Multiplication de 2 nombres A et B sur N bits signés en C 2 • Cpt est un compteur de séquence (N) • BC est un registre de 2 bits (fenêtre) • B et A sont des registres de N et N+1 bits. – Initialement B est chargé dans le registre B – A est chargé dans A et son signe est recopié dans le bit de poids fort (AN et AN-1 ont même valeur) • Les registres B et BC concaténés sont notés B: BC, donc B: BC a N+2 bits. • P (le résultat) a 2 N bits de long et contiendra le produit final. Les N+1 bits de poids fort sont appelés PH et les N-1 de poids faibles PL. 87

Algorithme de Booth • 1. Initialisation: – Le multiplicande est chargé dans A (et étendu à N+1 bits), le multiplieur dans B. – La valeur N est chargée dans Cpt. – P et BC sont initialisés à zéro • 2. Décalage arithmétique à droite: ashift (recopie du bit de poids fort) préserve le signe d'un nombre en complément à 2 (c'est une division par 2). – Faire un ashift sur P – Faire ashift sur B: BC • 3. Addition, Soustraction, ou Nop: – si BC = 01 alors Additionner A à PH, sinon – si BC = 10 alors Soustraire A à PH. (pour soustraire, faire le complément à 2 et additionner) – sinon (BC = 00 ou 11) ne rien faire Nop • 4. Décrémenter Cpt, si Cpt ≠ 0, retourner en 2 sinon fin 88

Exemple : N=5, P= (-5) * (+2) B= -5 (11011 b) A= +2 (00010 b). Le complément à 2 de A est 111110 b Etapes 1 B 11011 BC 00 PH 000000 2 11101 10 000000 111110+ -----111110 0000 4 3 3, 4 PL 0000 2, 3, 4 11110 111111 2 11111 01 111111 1000 000010+ -----000001 1000 3, 4 2 11111 10 3, 4 2, 3, 4 11111 0000 Cpt 5 soustraction addition 2 000000 111110+ -----111110 1100 1 111111 0 0110 nop soustraction nop Résultat : 1111110110 b est le complément à 2 de 00000010102 = 10 c. à. d. -10 89

Améliorations • Alors qu'avec cette version , on utilise un additionneur N+1 bits, on peut n'utiliser qu'un additionneur N bits (mais il faut gérer le dépassement de capacité en complément à 2) • Chaque itération comporte une opération de décalage, donc les étapes 2 et 3 peuvent être combinées pour gagner du temps. • Finalement, on peut éliminer le registre B, en se servant de PH pour mémoriser le multiplicande. 90

Multiplieur virgule flottante Exemple : P= A*B= 452, 5*117, 5 Signe du produit : "ouex" des bits de signe Exposant du produit : Somme des exposants Eb(P)= E(P)+127 = Eb(A)-127+Eb(B)-127+127 = Eb(A)+Eb(B)-127 Mantisse du produit : Produit des mantisses et recadrage => modification de l'exposant 91

Division 92

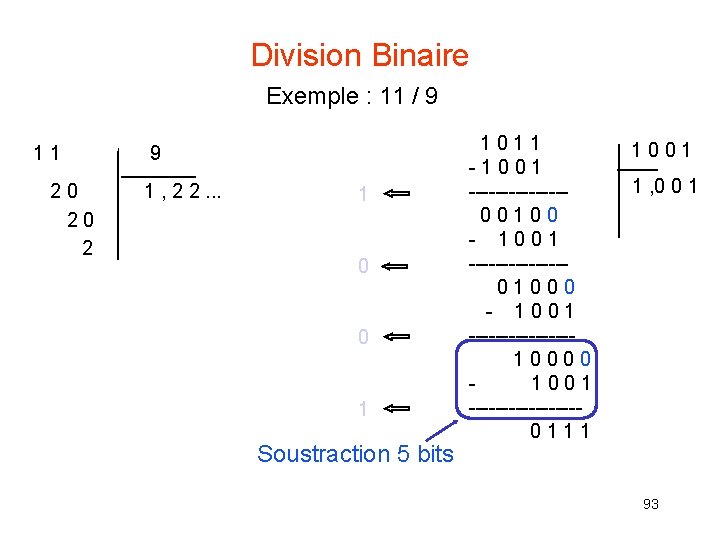
Division Binaire Exemple : 11 / 9 1 1 9 2 0 1 , 2 2. . . 2 0 2 1 0 0 1 Soustraction 5 bits 1 0 1 1 - 1 0 0 1 ------- 0 0 1 0 0 - 1 0 0 1 ------- 0 1 0 0 0 - 1 0 0 1 -------- 1 0 0 - 1 0 0 1 -------- 0 1 1 0 0 1 1 , 0 0 1 93

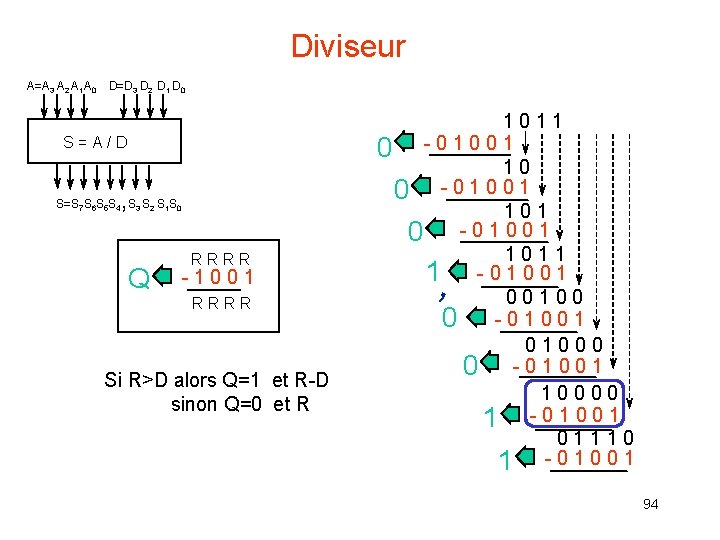
Diviseur A=A 3 A 2 A 1 A 0 D=D 3 D 2 D 1 D 0 S = A / D , S=S 7 S 6 S 5 S 4 S 3 S 2 S 1 S 0 Q R R - 1 0 0 1 R R Si R>D alors Q=1 et R-D sinon Q=0 et R 1 0 1 1 0 - 0 1 0 0 1 1 0 1 0 - 0 1 0 0 1 1 1 - 0 1 0 0 0 - 0 1 0 1 0 0 - 0 1 0 0 1 - 0 1 0 1 1 1 0 1 - 0 1 0 0 1 , 94

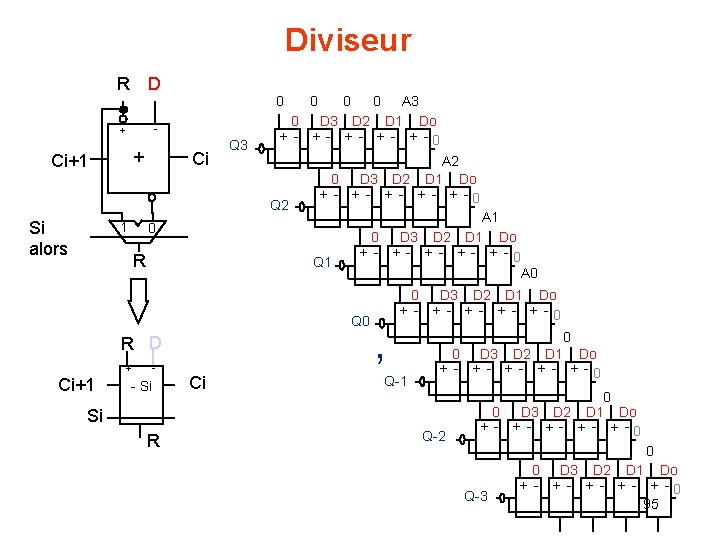
Diviseur R D 0 - + + Ci+1 Ci Q 3 A 3 0 D 3 D 2 D 1 Do + - + - + -0 Q 2 Si alors 1 0 0 A 2 0 D 3 D 2 D 1 Do + - + - + -0 0 R 0 Q 1 A 1 0 D 3 D 2 D 1 Do + - + - + -0 A 0 Q 0 R D Ci+1 + - - Si Ci , 0 D 3 D 2 D 1 Do + - + - + -0 Q-1 0 0 D 3 D 2 D 1 Do + - + - + -0 Si R Q-2 0 0 D 3 D 2 D 1 Do + - + - + -0 0 Q-3 0 D 3 D 2 D 1 Do + - + - + -0 95

Divisions multiplication de polynômes dans GF(2 n) 96

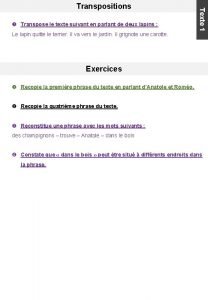
Espace des polynômes • Suite de bits de p bits élément de [GF(2)]p coefficients du polynôme ap-1 x(p-1)+ap-2 x(p-2)+…+a 0 Ex : 101001 1. x 5+0. x 4+1. x 3+0. x 2+0. x+1 = x 5+x 3+1 • Pp-1 (ensemble des polys de degré < p) isomorphe à [GF(2)]p Attention : degré du poly = p-1 • Structure d'espace vectoriel sur GF[2] • Division polynomiale – P 1(x) = P 2(x). Q(x)+R(x) avec R(x)=0 ou deg(R)<deg(P 2) – exemple : x 3+x 2+x=(x+1)(x 2+1) + 1 • Structure d'anneau 97

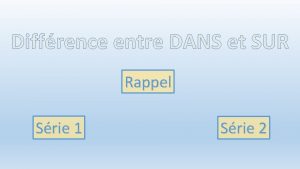
Division de Polynômes Division dans [GF(2)]p P 1(x) = P 2(x). Q(x)+R(x) avec R(x)=0 ou deg(R)<deg(P 2) Calcul du reste Si degré(P 1(x)) = degré (P 2(x)) alors Q(x) = 1 et R(x) = P 1(x) – P 2(x). 1 = P 1(x) – P 2(x) = P 1(x) + P 2(x) exemple : 11011 divisé par 11100 x 4+x 3+x+1 divisé par x 4+x 3+x Q(x)=1 et R(x) = (11011) + (11100) = (00111) = x 2+x+1 2 Si degré(P 1(x)) < degré(P 2(x)) alors Q(x) =0 et R(x) = P 1(x) 98

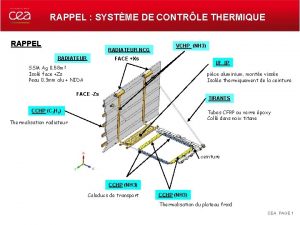
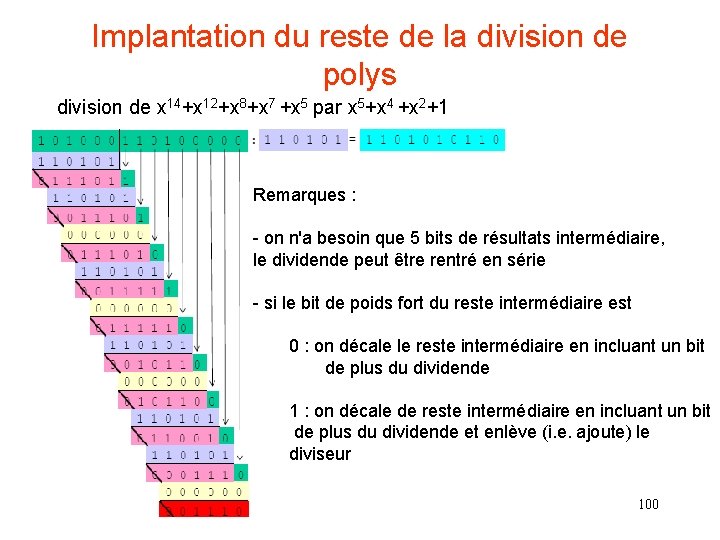
Implantation du reste de la division de polynômes dans (GF[2])n reste de la division de x 14+x 12+x 8+x 7+x 5 par x 5+x 4 +x 2+1 x 14+x 12+x 8+x 7+x 5 = (x 5+x 4+x 2+1) (x 9+x 8+x 6+x 4+x 2+x) + (x 3+x 2+x) Quotient Reste = Syndrome 99

Implantation du reste de la division de polys division de x 14+x 12+x 8+x 7 +x 5 par x 5+x 4 +x 2+1 Remarques : - on n'a besoin que 5 bits de résultats intermédiaire, le dividende peut être rentré en série - si le bit de poids fort du reste intermédiaire est 0 : on décale le reste intermédiaire en incluant un bit de plus du dividende 1 : on décale de reste intermédiaire en incluant un bit de plus du dividende et enlève (i. e. ajoute) le diviseur 100

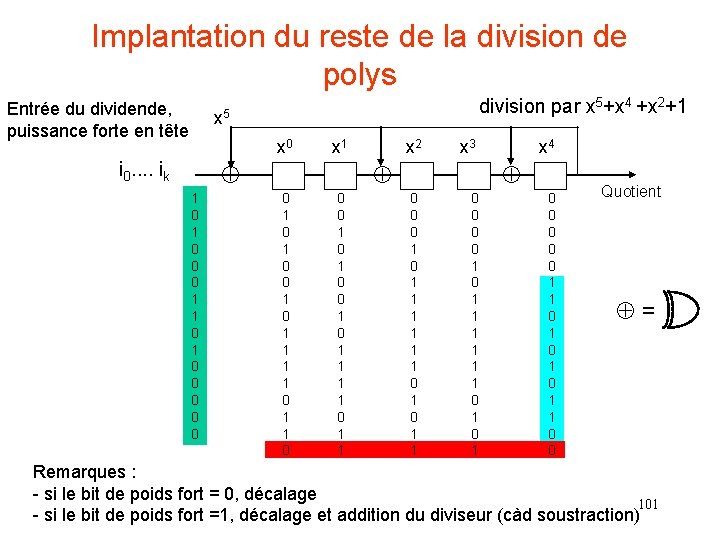
Implantation du reste de la division de polys Entrée du dividende, puissance forte en tête division par x 5+x 4 +x 2+1 x 5 x 0 i 0. . ik x 1 1 0 0 0 1 1 0 0 0 x 2 x 3 0 1 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 x 4 0 0 0 1 1 1 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 1 0 1 1 0 0 Quotient = Remarques : - si le bit de poids fort = 0, décalage 101 - si le bit de poids fort =1, décalage et addition du diviseur (càd soustraction)

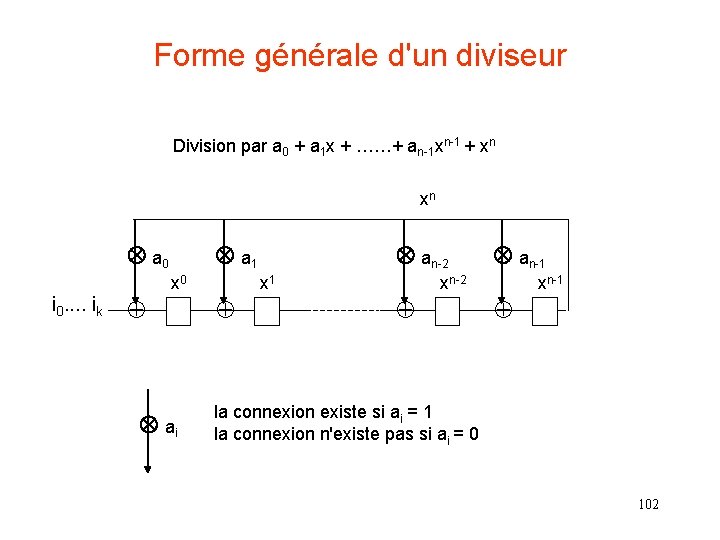
Forme générale d'un diviseur Division par a 0 + a 1 x + ……+ an-1 xn-1 + xn xn a 0 a 1 x 0 i 0. . ik ai an-2 x 1 an-1 xn-2 xn-1 la connexion existe si ai = 1 la connexion n'existe pas si ai = 0 102

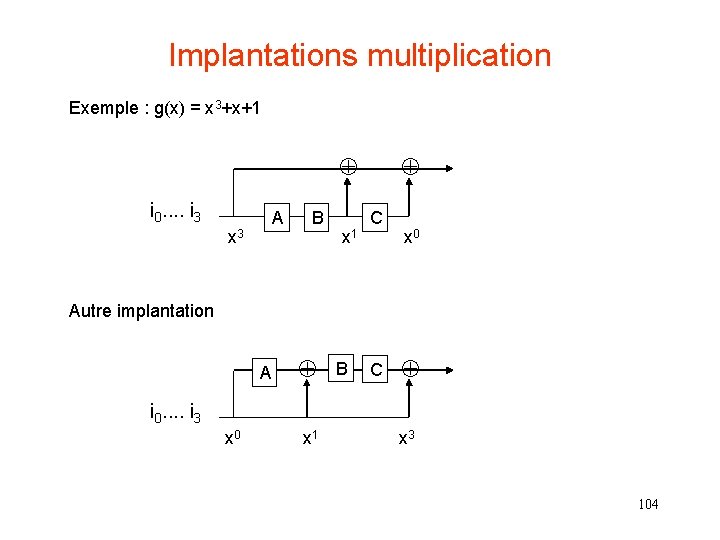
Implantation de la multiplication de polynômes • Multiplication de polynômes par un polynôme g(x) = x 3+x+1 Exemple : soit à calculer i(x). g(x) avec g(x) = x 3+x+1, i(x) = x 3+x 2+1 1101 i 0. . i 3 1011 A x 3 B t C x x 0 Initialement les bascules A, B, C sont à 0 E 0 ABC Sortie 000 1 i 3 =1 100 1 x 6 2 i 2=1 110 1 x 5 3 i 1=0 011 1 x 4 4 i 0=1 101 1 x 3 5 0 010 1 x 2 6 0 001 1 x 1 7 0 000 1 x 0 103

Implantations multiplication Exemple : g(x) = x 3+x+1 i 0. . i 3 A x 3 B x 1 C x 0 Autre implantation A B C i 0. . i 3 x 0 x 1 x 3 104

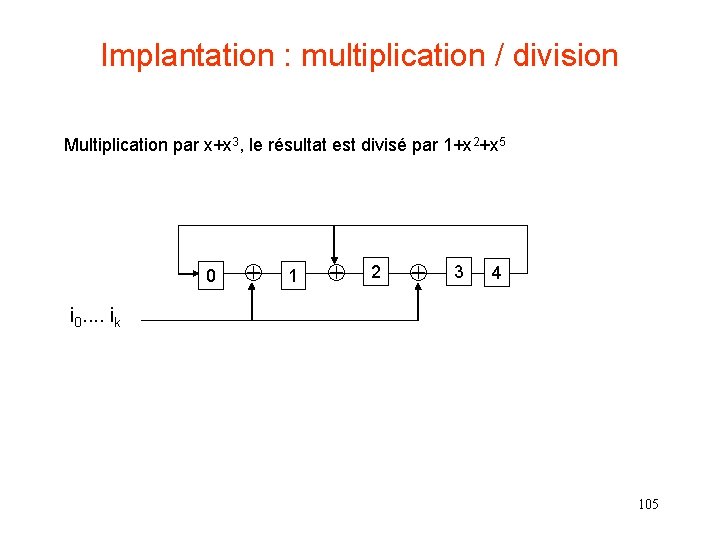
Implantation : multiplication / division Multiplication par x+x 3, le résultat est divisé par 1+x 2+x 5 0 1 2 3 4 i 0. . ik 105

Applications • Codes correcteurs (codes cycliques) – codage : multiplication ou division de polynomes : c(x)= i(x). g(x). – contrôle : division de polynomes – un code cyclique admet un poly. de contrôle p(x) / xn+1 = p(x). g(x). c(x) C p(x). c(x) mod(xn+1) = 0 • Test – BIST (Built-In Self Test) – Génération de nombres pseudo-aléatoires – Compression de réponses – Division de polynomes 106

Exercice • Soit un code polynomial de dimension 3 de poly. générateur x 2+x+1 • Quel est la taille des codes ? • Calculer les codes par multiplication de polys et par matrice génératrice • Proposer une structure pour le codage et le détection d'erreurs – implantation parallèle – implantation série – vérifier les structures sur des exemples significatifs. 107