11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND



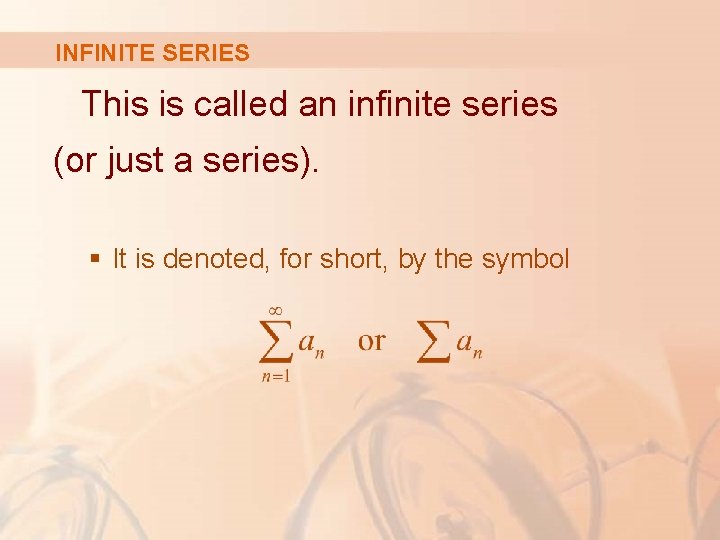


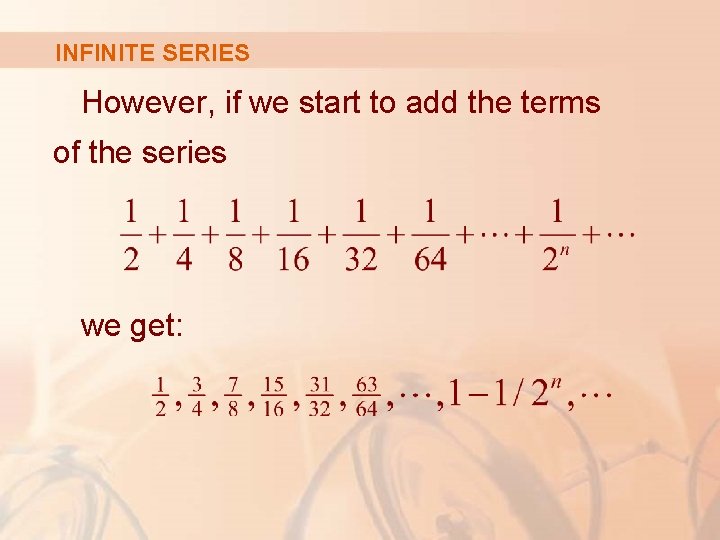
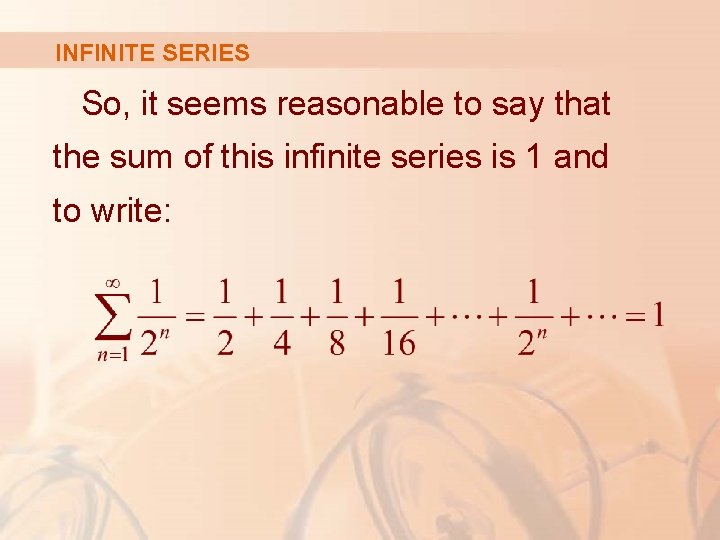



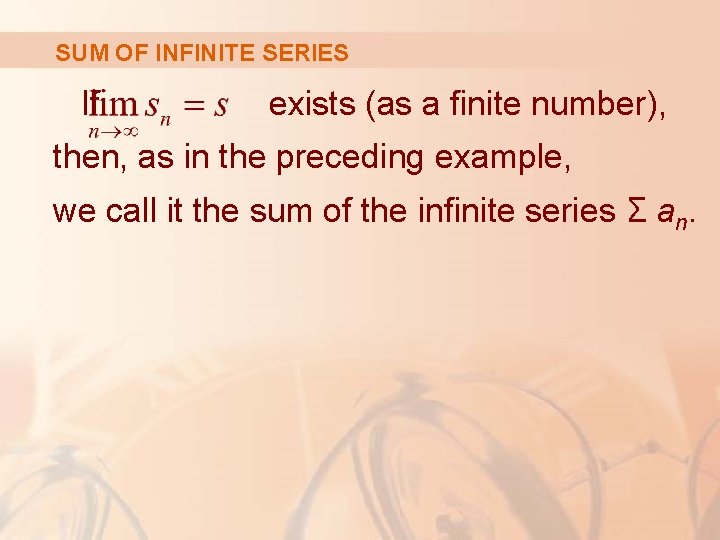



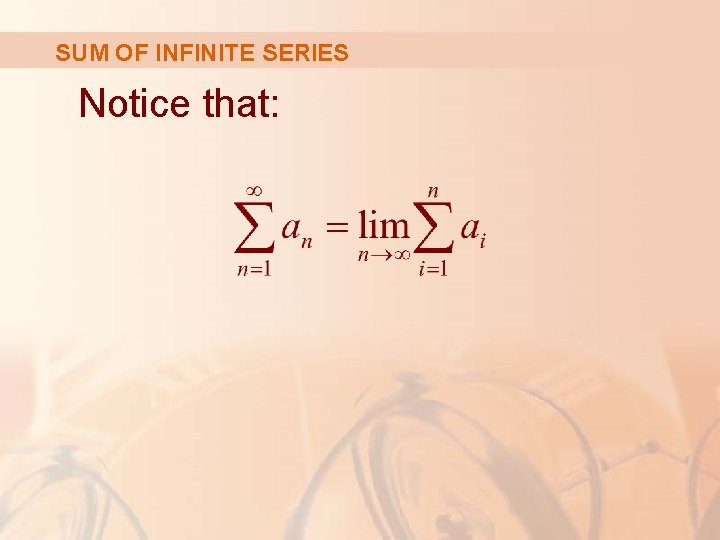





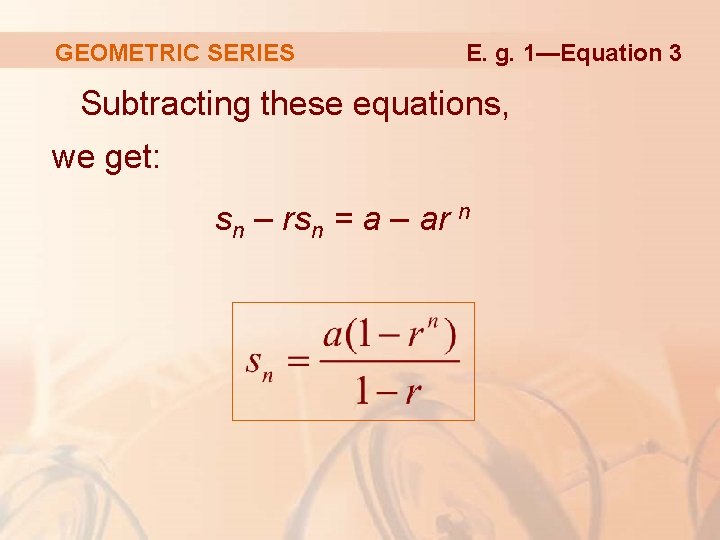












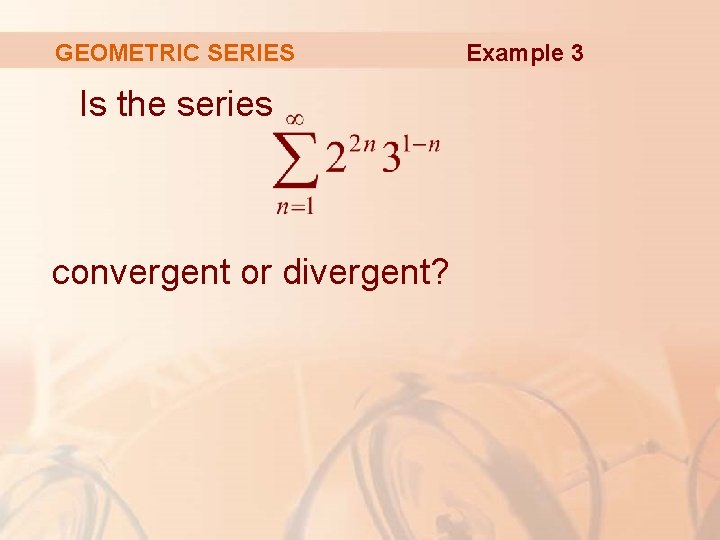





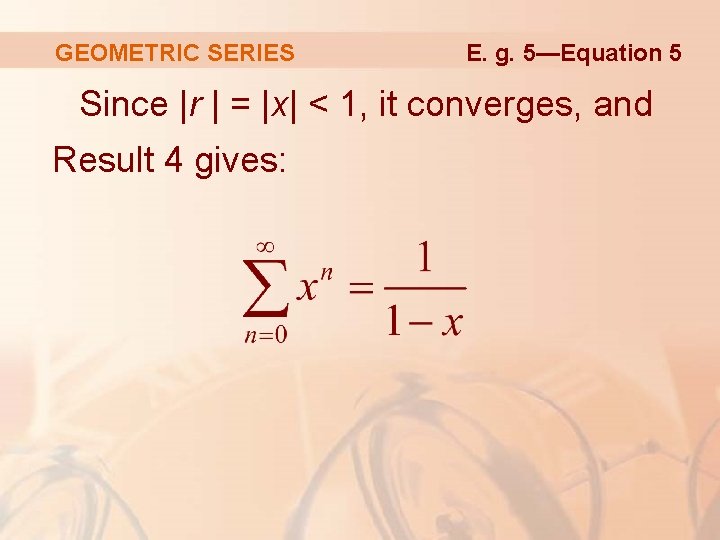



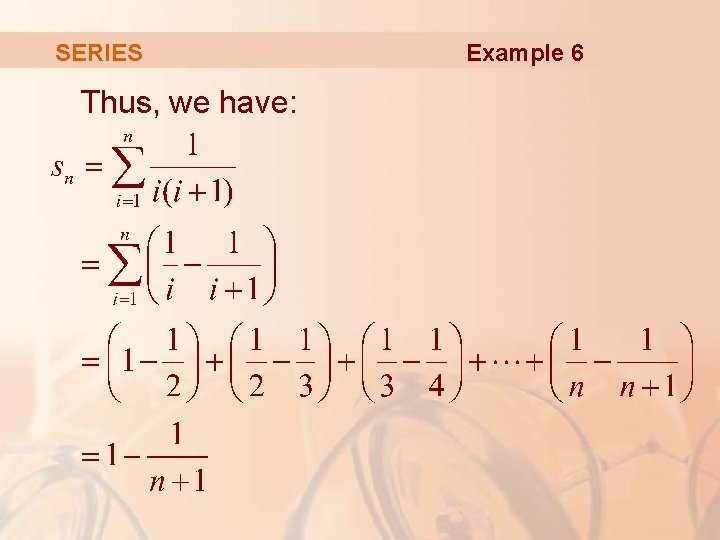



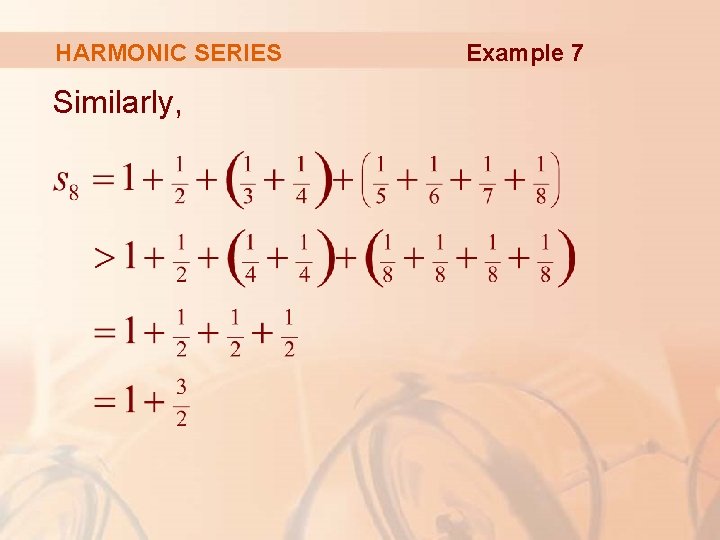













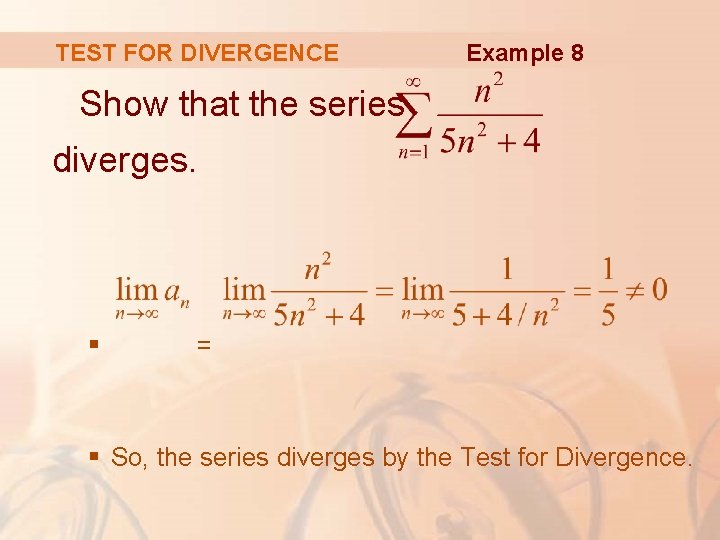













- Slides: 78

11 INFINITE SEQUENCES AND SERIES

INFINITE SEQUENCES AND SERIES 11. 2 Series In this section, we will learn about: Various types of series.

Series 1 SERIES If we try to add the terms of an infinite sequence we get an expression of the form a 1 + a 2 + a 3 + ··· + an + ∙·∙
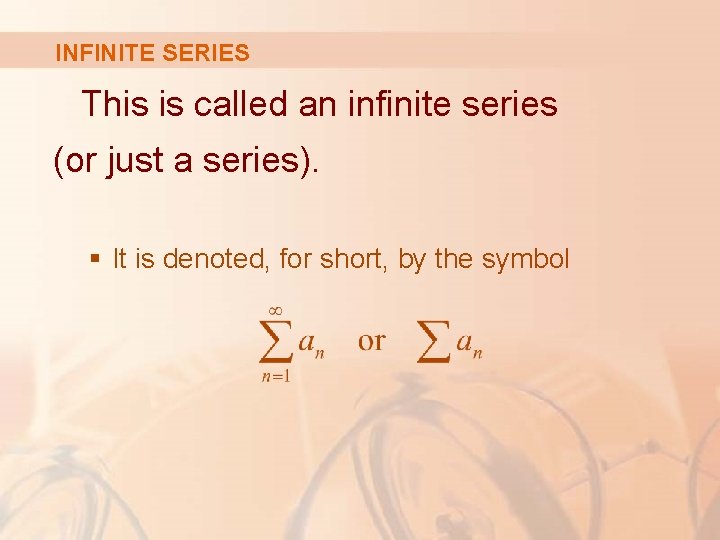
INFINITE SERIES This is called an infinite series (or just a series). § It is denoted, for short, by the symbol

INFINITE SERIES However, does it make sense to talk about the sum of infinitely many terms?

INFINITE SERIES It would be impossible to find a finite sum for the series 1 + 2 + 3 + 4 + 5 + ∙∙∙ + n + ··· § If we start adding the terms, we get the cumulative sums 1, 3, 6, 10, 15, 21, . . . § After the nth term, we get n(n + 1)/2, which becomes very large as n increases.
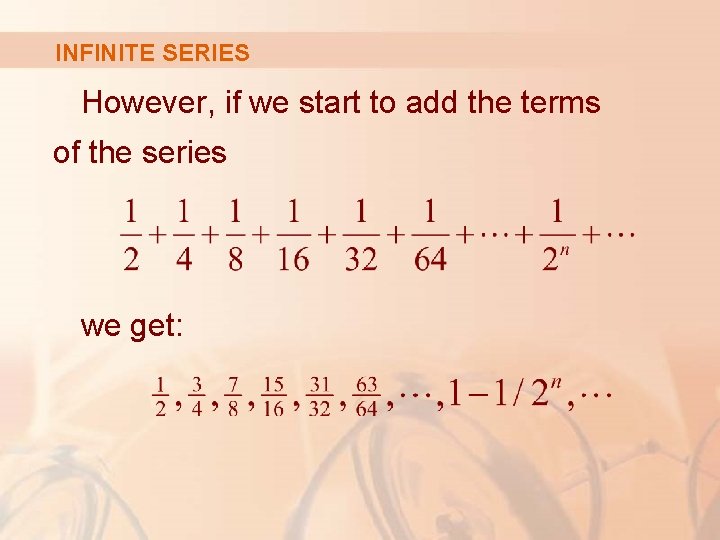
INFINITE SERIES However, if we start to add the terms of the series we get:

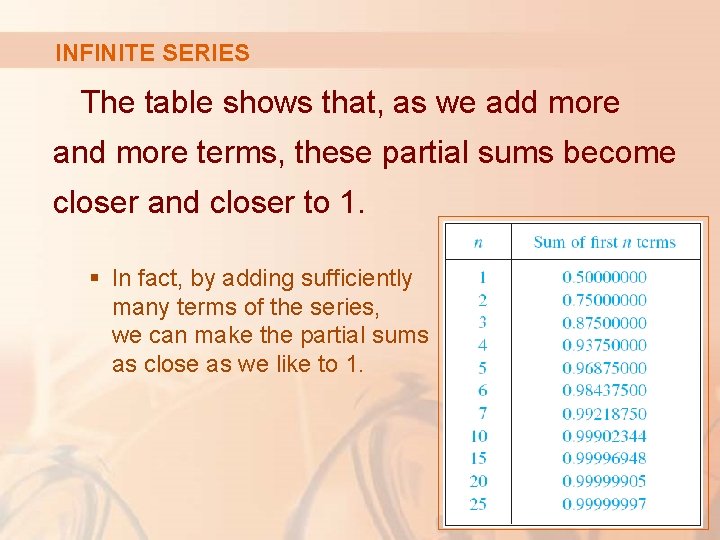
INFINITE SERIES The table shows that, as we add more and more terms, these partial sums become closer and closer to 1. § In fact, by adding sufficiently many terms of the series, we can make the partial sums as close as we like to 1.
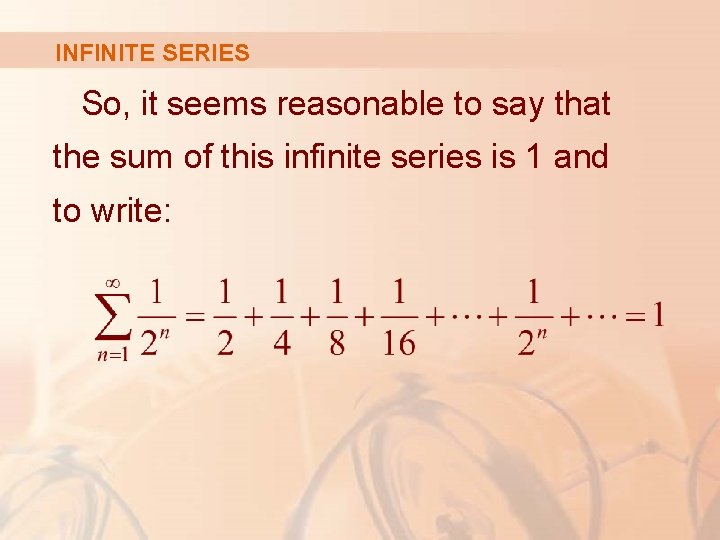
INFINITE SERIES So, it seems reasonable to say that the sum of this infinite series is 1 and to write:

INFINITE SERIES We use a similar idea to determine whether or not a general series (Series 1) has a sum.

INFINITE SERIES We consider the partial sums s 1 = a 1 s 2 = a 1 + a 2 s 3 = a 1 + a 2 + a 3 + a 4 § In general,

INFINITE SERIES These partial sums form a new sequence {sn}, which may or may not have a limit.
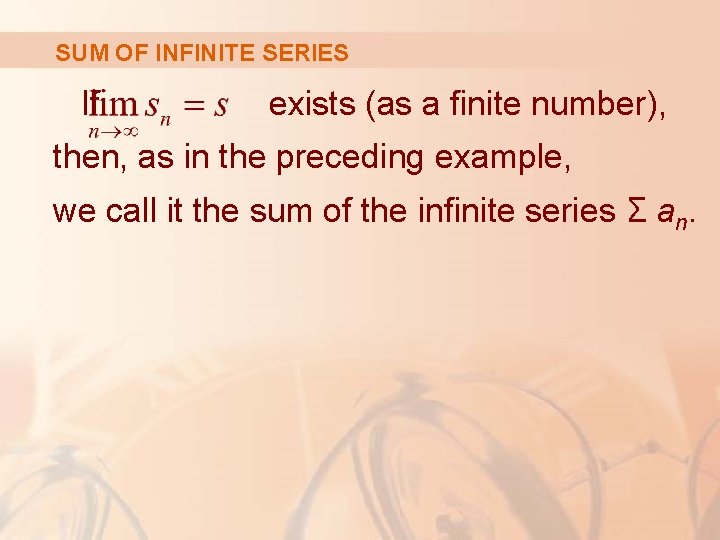
SUM OF INFINITE SERIES If exists (as a finite number), then, as in the preceding example, we call it the sum of the infinite series Σ an.

SUM OF INFINITE SERIES Definition 2 Given a series let sn denote its nth partial sum:

SUM OF INFINITE SERIES Definition 2 If the sequence {sn} is convergent and exists as a real number, then the series Σ an is called convergent and we write: § The number s is called the sum of the series. § Otherwise, the series is called divergent.

SUM OF INFINITE SERIES Thus, the sum of a series is the limit of the sequence of partial sums. § So, when we write , we mean that, by adding sufficiently many terms of the series, we can get as close as we like to the number s.
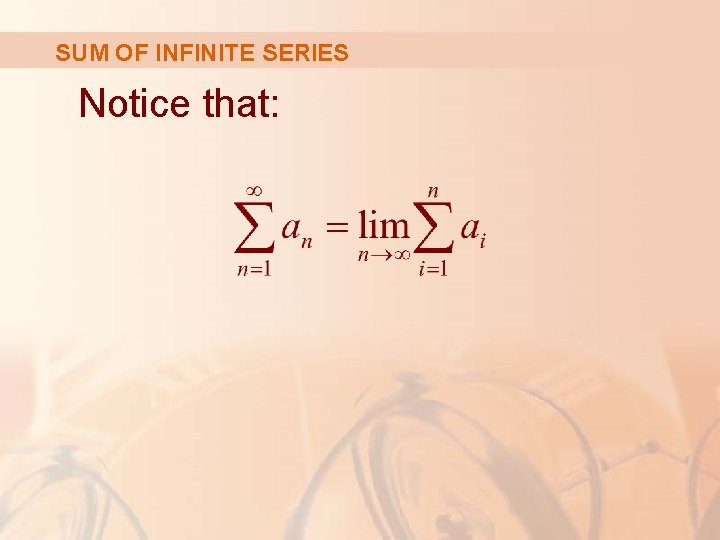
SUM OF INFINITE SERIES Notice that:

SUM OF INFINITE SERIES VS. IMPROPER INTEGRALS Compare with the improper integral § To find this integral, we integrate from 1 to t and then let t → ∞. § For a series, we sum from 1 to n and then let n → ∞.

GEOMETRIC SERIES Example 1 An important example of an infinite series is the geometric series

GEOMETRIC SERIES Example 1 Each term is obtained from the preceding one by multiplying it by the common ratio r. § We have already considered the special case where a = ½ and r = ½ earlier in the section.

GEOMETRIC SERIES Example 1 If r = 1, then sn = a + ∙∙∙ + a = na → ±∞ § Since doesn’t exist, the geometric series diverges in this case.

GEOMETRIC SERIES Example 1 If r ≠ 1, we have sn = a + ar 2 + ∙∙∙ + ar n– 1 and rsn = ar + ar 2 + ∙∙∙ +ar n– 1 + ar n
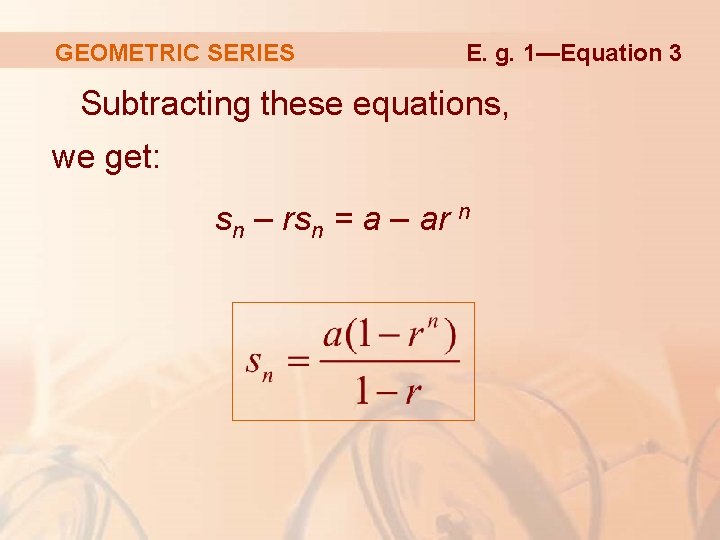
GEOMETRIC SERIES E. g. 1—Equation 3 Subtracting these equations, we get: sn – rsn = a – ar n

GEOMETRIC SERIES Example 1 If – 1 < r < 1, we know from Result 9 in Section 11. 1 that r n → 0 as n → ∞. So, § Thus, when |r | < 1, the series is convergent and its sum is a/(1 – r).

GEOMETRIC SERIES Example 1 If r ≤ – 1 or r > 1, the sequence {r n} is divergent by Result 9 in Section 11. 1 So, by Equation 3, does not exist. § Hence, the series diverges in those cases.

GEOMETRIC SERIES The figure provides a geometric demonstration of the result in Example 1.

GEOMETRIC SERIES If s is the sum of the series, then, by similar triangles, So,

GEOMETRIC SERIES We summarize the results of Example 1 as follows.

GEOMETRIC SERIES The geometric series is convergent if |r | < 1. Result 4

GEOMETRIC SERIES Result 4 The sum of the series is: If |r | ≥ 1, the series is divergent.

GEOMETRIC SERIES Example 2 Find the sum of the geometric series § The first term is a = 5 and the common ratio is r = – 2/3

GEOMETRIC SERIES Example 2 § Since |r | = 2/3 < 1, the series is convergent by Result 4 and its sum is:

GEOMETRIC SERIES What do we really mean when we say that the sum of the series in Example 2 is 3? § Of course, we can’t literally add an infinite number of terms, one by one.

GEOMETRIC SERIES However, according to Definition 2, the total sum is the limit of the sequence of partial sums. § So, by taking the sum of sufficiently many terms, we can get as close as we like to the number 3.

GEOMETRIC SERIES The table shows the first ten partial sums sn. The graph shows how the sequence of partial sums approaches 3.
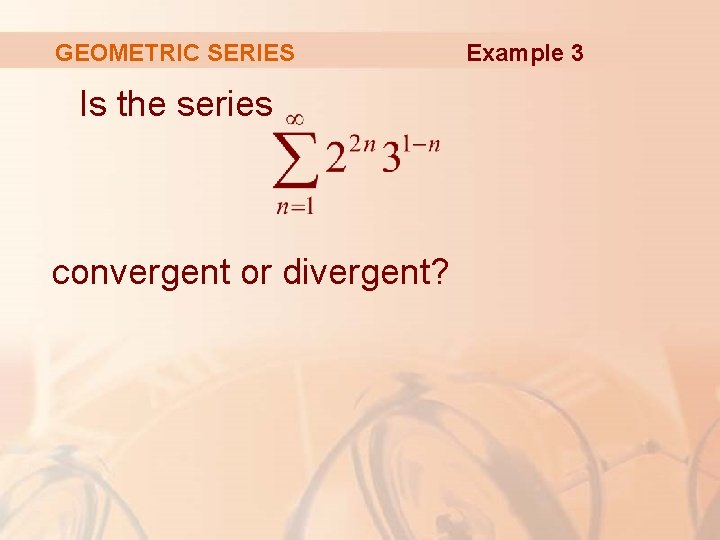
GEOMETRIC SERIES Is the series convergent or divergent? Example 3

GEOMETRIC SERIES Example 3 Let’s rewrite the nth term of the series in the form ar n-1: § We recognize this series as a geometric series with a = 4 and r = 4/3. § Since r > 1, the series diverges by Result 4.

GEOMETRIC SERIES Example 4 Write the number as a ratio of integers. § 2. 3171717… § After the first term, we have a geometric series with a = 17/103 and r = 1/102.

GEOMETRIC SERIES § Therefore, Example 4

GEOMETRIC SERIES Example 5 Find the sum of the series where |x| < 1. § Notice that this series starts with n = 0. § So, the first term is x 0 = 1. § With series, we adopt the convention that x 0 = 1 even when x = 0.

GEOMETRIC SERIES Thus, § This is a geometric series with a = 1 and r = x. Example 5
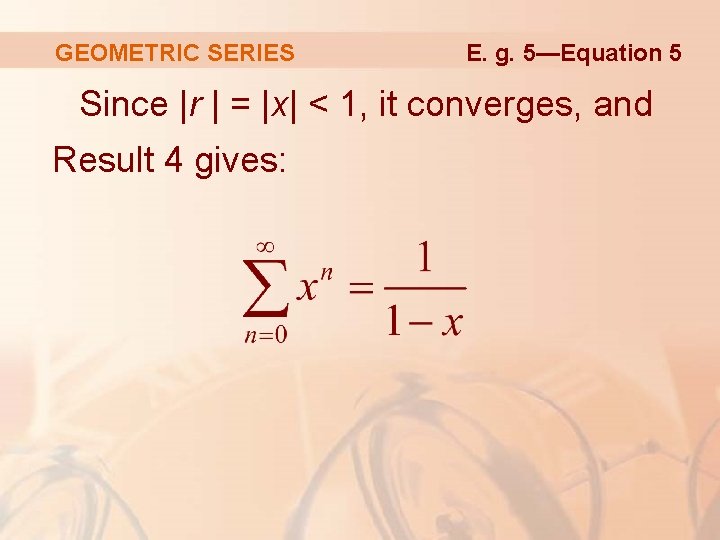
GEOMETRIC SERIES E. g. 5—Equation 5 Since |r | = |x| < 1, it converges, and Result 4 gives:

SERIES Example 6 Show that the series is convergent, and find its sum.

SERIES Example 6 This is not a geometric series. § So, we go back to the definition of a convergent series and compute the partial sums:

SERIES Example 6 We can simplify this expression if we use the partial fraction decomposition. § See Section 7. 4
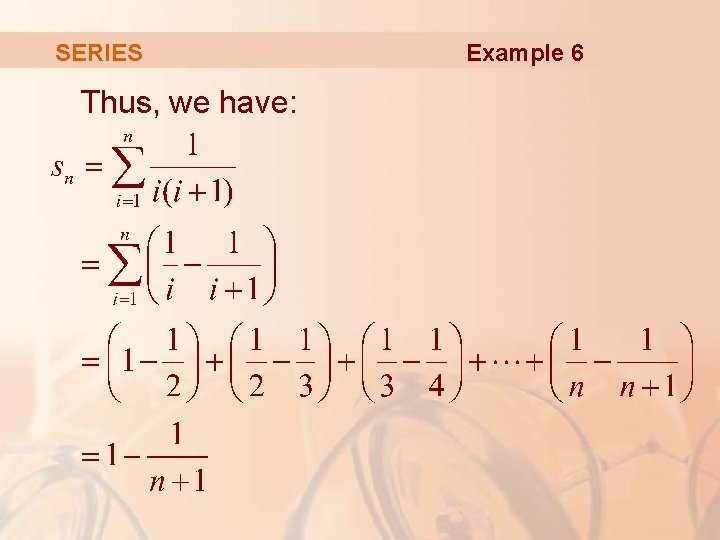
SERIES Thus, we have: Example 6

SERIES Example 6 Thus, § Hence, the given series is convergent and

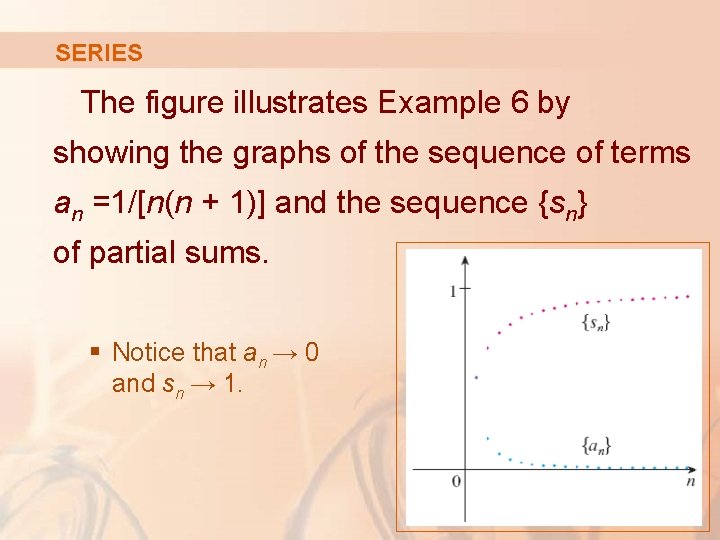
SERIES The figure illustrates Example 6 by showing the graphs of the sequence of terms an =1/[n(n + 1)] and the sequence {sn} of partial sums. § Notice that an → 0 and sn → 1.

HARMONIC SERIES Example 7 Show that the harmonic series is divergent.

HARMONIC SERIES Example 7 For this particular series it’s convenient to consider the partial sums s 2, s 4, s 8, s 16, s 32, … and show that they become large.
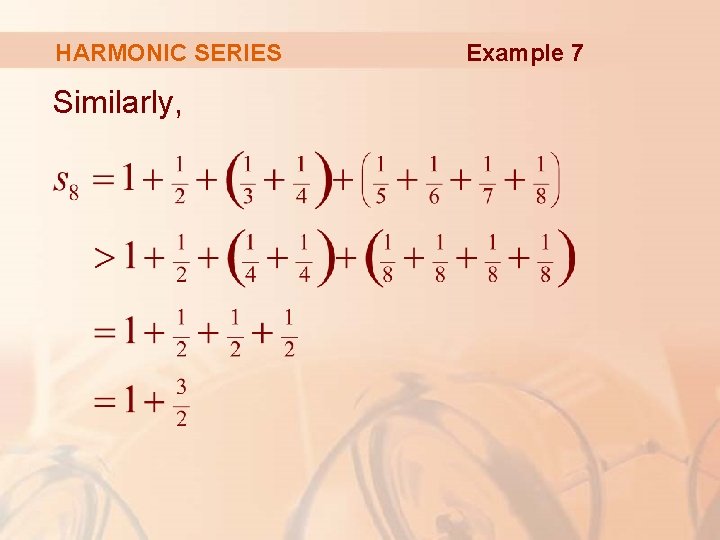
HARMONIC SERIES Similarly, Example 7

HARMONIC SERIES Similarly, Example 7

HARMONIC SERIES Example 7 Similarly, s 32 > 1 + 5/2, s 64 > 1 + 6/2, and, in general, § This shows that s 2 n → ∞ as n → ∞, and so {sn} is divergent. § Therefore, the harmonic series diverges.

HARMONIC SERIES The method used in Example 7 for showing that the harmonic series diverges is due to the French scholar Nicole Oresme (1323– 1382).

SERIES If the series then Theorem 6 is convergent,

SERIES Theorem 6—Proof Let sn = a 1 + a 2 + ∙∙∙ + an Then, an = sn – sn– 1 § Since Σ an is convergent, the sequence {sn} is convergent.

SERIES Theorem 6—Proof Let Since n – 1 → ∞ as n → ∞, we also have:

SERIES Therefore, Theorem 6—Proof

SERIES Note 1 With any series Σ an we associate two sequences: § The sequence {sn} of its partial sums § The sequence {an} of its terms

SERIES Note 1 If Σ an is convergent, then § The limit of the sequence {sn} is s (the sum of the series). § The limit of the sequence {an}, as Theorem 6 asserts, is 0.

Note 2 SERIES The converse of Theorem 6 is not true in general. § If , we cannot conclude that Σ an is convergent.

SERIES Note 2 Observe that, for the harmonic series Σ 1/n, we have an = 1/n → 0 as n → ∞. § However, we showed in Example 7 that Σ 1/n is divergent.

THE TEST FOR DIVERGENCE If Test 7 does not exist or if then the series is divergent. ,

TEST FOR DIVERGENCE The Test for Divergence follows from Theorem 6. § If the series is not divergent, then it is convergent. § Thus,
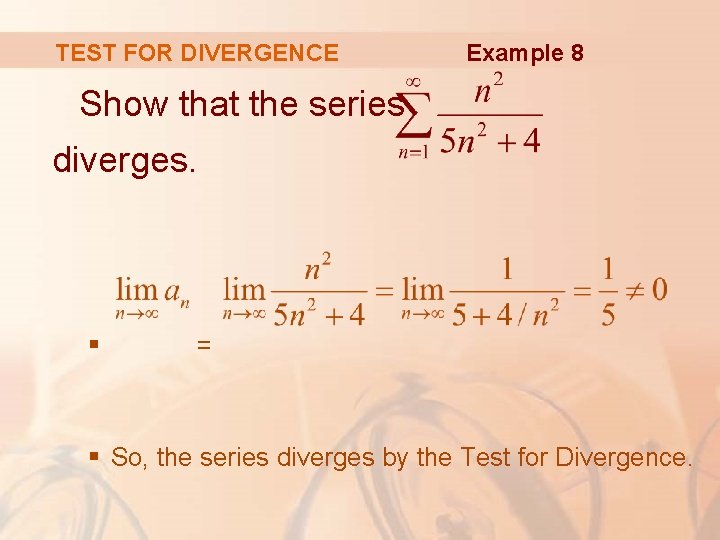
TEST FOR DIVERGENCE Example 8 Show that the series diverges. § = § So, the series diverges by the Test for Divergence.

SERIES If we find that Note 3 , we know that Σ an is divergent. If we find that , we know nothing about the convergence or divergence of Σ an.

SERIES Note 3 Remember the warning in Note 2: § If , the series Σ an might converge or diverge.

SERIES Theorem 8 If Σ an and Σ bn are convergent series, then so are the series Σ can (where c is a constant), Σ (an + bn), and Σ (an – bn), and

SERIES These properties of convergent series follow from the corresponding Limit Laws for Sequences in Section 11. 1 § For instance, we prove part ii of Theorem 8 as follows.

THEOREM 8 ii—PROOF Let

THEOREM 8 ii—PROOF The nth partial sum for the series Σ (an + bn) is:

THEOREM 8 ii—PROOF Using Equation 10 in Section 5. 2, we have:

THEOREM 8 ii—PROOF Hence, Σ (an + bn) is convergent, and its sum is:

SERIES Example 9 Find the sum of the series § The series Σ 1/2 n is a geometric series with a = ½ and r = ½. § Hence,

SERIES Example 9 § In Example 6, we found that: § So, by Theorem 8, the given series is convergent and

SERIES Note 4 A finite number of terms doesn’t affect the convergence or divergence of a series.

SERIES Note 4 For instance, suppose that we were able to show that the series § Since it follows that the entire series is convergent.

SERIES Note 4 Similarly, if it is known that the series converges, then the full series is also convergent.
 1/4^n convergence
1/4^n convergence Infinite diversity in infinite combinations
Infinite diversity in infinite combinations Arithmetic and geometric sequences and series
Arithmetic and geometric sequences and series Differentiate finite sequence and infinite sequence
Differentiate finite sequence and infinite sequence Unit 10 sequences and series homework 2 answers
Unit 10 sequences and series homework 2 answers Unit 10 sequences and series homework 1 answers
Unit 10 sequences and series homework 1 answers Chapter 12 sequences and series answers
Chapter 12 sequences and series answers 10-3 geometric sequences and series
10-3 geometric sequences and series Module 12 sequences and series answers
Module 12 sequences and series answers 10-3 practice geometric sequences and series answers
10-3 practice geometric sequences and series answers 10-2 arithmetic sequences and series answer key
10-2 arithmetic sequences and series answer key 10-1 sequences series and sigma notation
10-1 sequences series and sigma notation Sum of gp formula
Sum of gp formula Sequence and series formula
Sequence and series formula Sequences and series math 20-1
Sequences and series math 20-1 Chapter 1 sequences and series
Chapter 1 sequences and series Chapter 1 sequences and series
Chapter 1 sequences and series Pre calc sequences and series
Pre calc sequences and series Sequences and series math 20-1
Sequences and series math 20-1 Sequences and series games
Sequences and series games Sum formula for arithmetic sequence
Sum formula for arithmetic sequence Sequences and series math 20-1
Sequences and series math 20-1 Series and sequence examples
Series and sequence examples Recursive formula for geometric sequence
Recursive formula for geometric sequence Sequences dr frost
Sequences dr frost Geometric series sum formula
Geometric series sum formula Sum of gp
Sum of gp Formula for infinite geometric series
Formula for infinite geometric series Sum of gp formula
Sum of gp formula L'hopital's rule
L'hopital's rule Ramanujan infinite series
Ramanujan infinite series Arithmetic series formula
Arithmetic series formula Geometric sequence formula sum
Geometric sequence formula sum Arithmetic sequence examples
Arithmetic sequence examples Summation notation
Summation notation Partial sum of arithmetic sequence
Partial sum of arithmetic sequence Series aiding and series opposing
Series aiding and series opposing Maclaurin series vs taylor series
Maclaurin series vs taylor series Heisenberg 1925 paper
Heisenberg 1925 paper Taylor series of composite function
Taylor series of composite function Deret maclaurin
Deret maclaurin Ibm p series servers
Ibm p series servers Shunt feedback amplifier analysis
Shunt feedback amplifier analysis Finite and infinite sets
Finite and infinite sets Horizontal
Horizontal Explecit formula
Explecit formula Geometric series formula
Geometric series formula Geomtric formula
Geomtric formula Module 4 patterns and sequences
Module 4 patterns and sequences Why are geometric sequences exponential functions
Why are geometric sequences exponential functions Arithmetic sequence sigma notation
Arithmetic sequence sigma notation Arithmetic sequence
Arithmetic sequence Lesson 3: arithmetic and geometric sequences
Lesson 3: arithmetic and geometric sequences Patterns and sequences module quiz b
Patterns and sequences module quiz b Geometric patterns formula
Geometric patterns formula Introduction to geometric sequences
Introduction to geometric sequences Sum formula for geometric sequence
Sum formula for geometric sequence Icwpcsd
Icwpcsd Hilbert's paradox of the grand hotel
Hilbert's paradox of the grand hotel Lyons township grading scale
Lyons township grading scale Reaching for the infinite heart
Reaching for the infinite heart Finite set example
Finite set example Diagramming sentences with prepositional phrases
Diagramming sentences with prepositional phrases Infinite regress
Infinite regress Gim model social work中文
Gim model social work中文 Area of koch snowflake
Area of koch snowflake What is finite loading
What is finite loading Electric field of infinite line
Electric field of infinite line Electric field of infinite line
Electric field of infinite line Infinite vector space
Infinite vector space Equivalent set example
Equivalent set example Set what is
Set what is Berea infinite campus
Berea infinite campus Oscillating discontinuity example
Oscillating discontinuity example Infinite set example
Infinite set example Duchamp fountain
Duchamp fountain Waiting line management system
Waiting line management system Sigma notation for geometric series
Sigma notation for geometric series Sd27j infinite campus
Sd27j infinite campus