Sequences and Series A sequence is an ordered




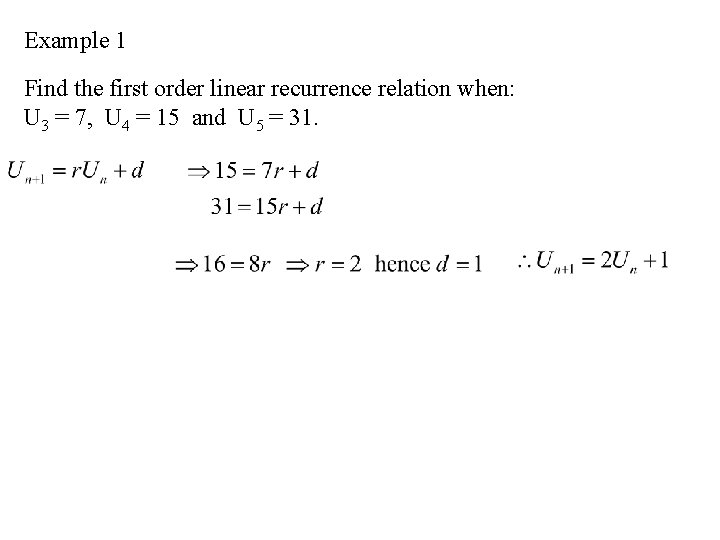




















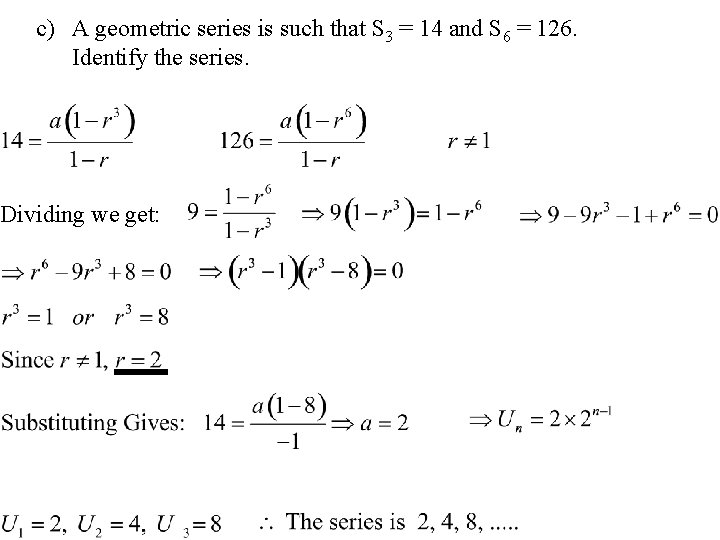
















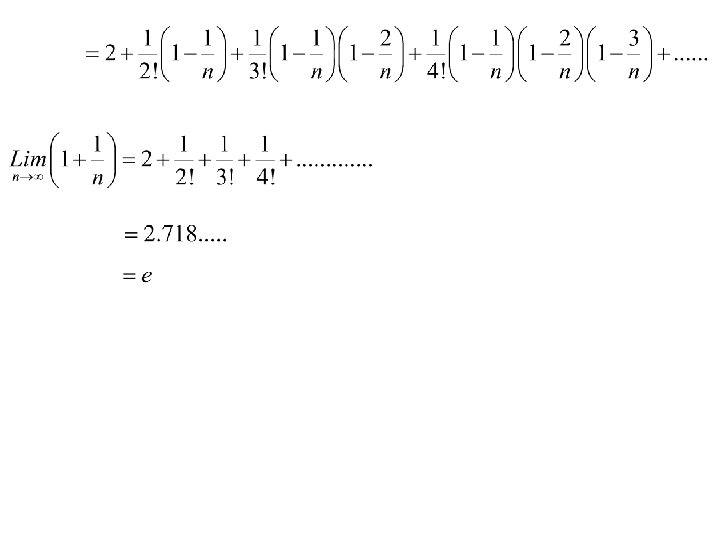

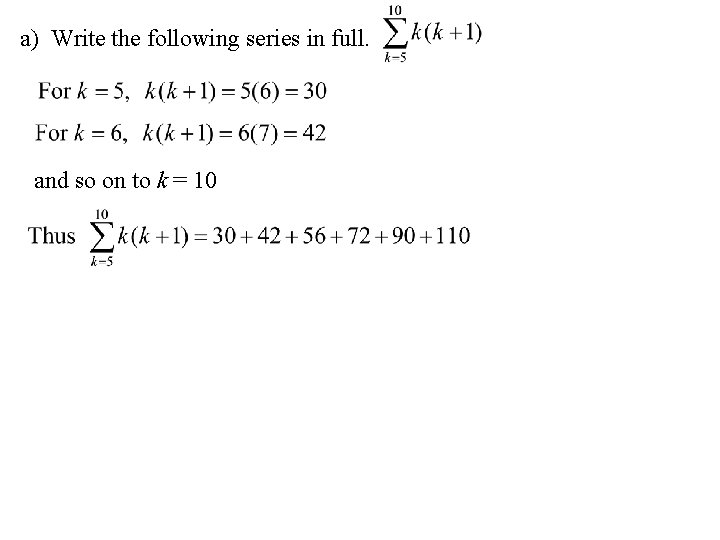
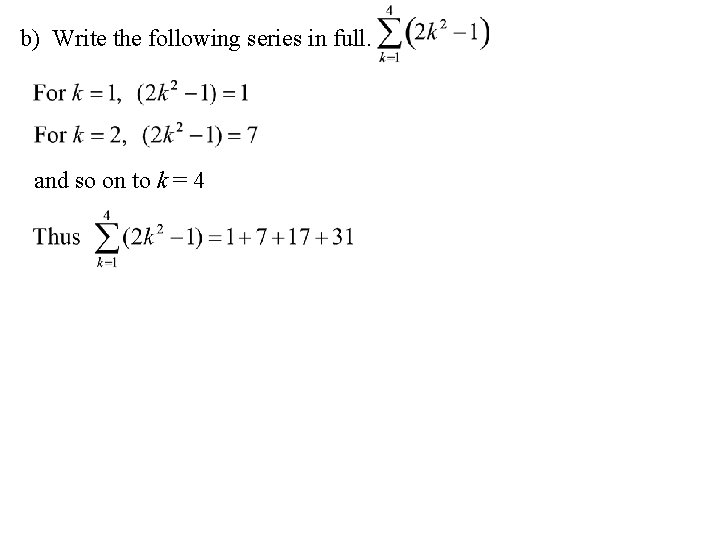


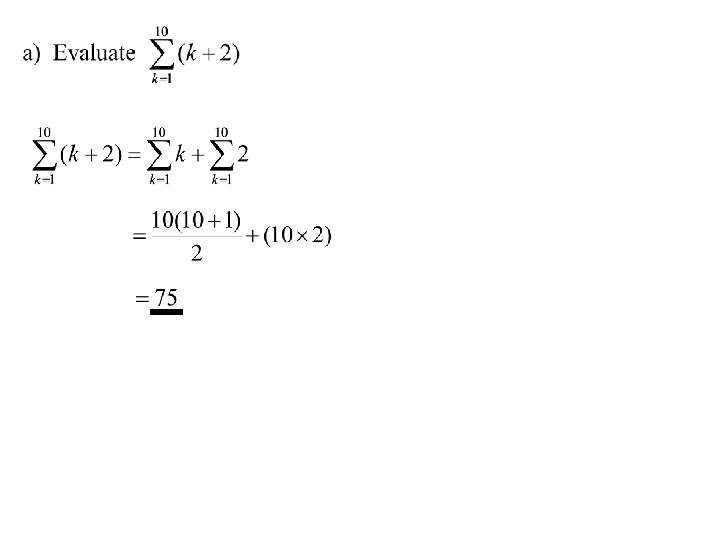


- Slides: 51

Sequences and Series A sequence is an ordered list of numbers where each term is obtained according to a fixed rule. A series, or progression, is a sum. The terms of which form a sequence. The nth term of a sequence is often denoted Un, so that, for example, U is the first term. A sequence can be defined by a recurrence relation where Un+1 is given as a function of lower, earlier terms.

A first – order recurrence relation is where Un+1=r. Un + d, where r and d are constants. This relation is linear. A sequence can be defined by a formula for Un, given as a function. Un = f(n) Being given the first few terms of a sequence is not enough to identify the sequence.

For example. Identify the next term in the sequence 1, 2, 3, …, …, Possible answers include: If however we also know that the sequence is generated by a first order linear recurrence relation, then we know

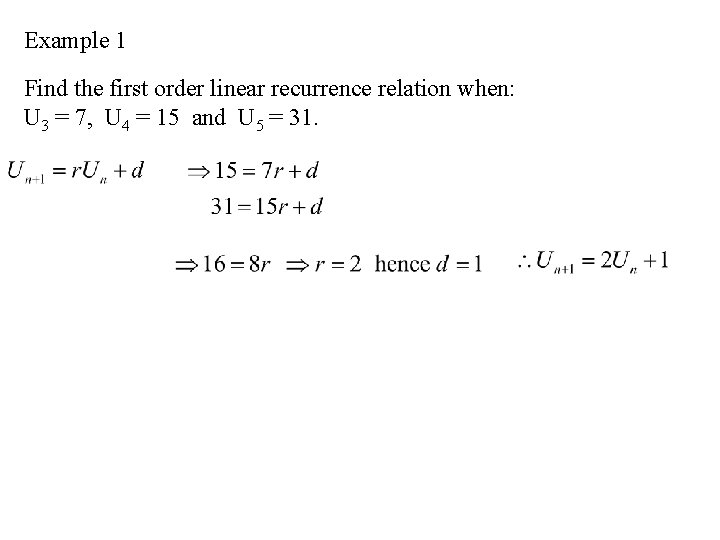
Example 1 Find the first order linear recurrence relation when: U 3 = 7, U 4 = 15 and U 5 = 31.

Note Given a relation When this repetition happens, Un is referred to as a fixed point. In this case, for any other value of Un, the relation generates values that move away or diverge from the value of 2. Un =2 is an unstable fixed point.

Given the relation , then if for some value of n, Un = 4, the sequence would proceed 4, 4, …… If any other value of Un is used apart from 4, the relation generates terms whose value moves towards or converges on 4. Un = 4 is a stable fixed point, often referred to as the limit of the recurrence relation. In general, for the relation , we have a fixed point when

Arithmetic Sequences If a sequence is generated so that, for all n, then the sequence is known as an arithmetic sequence. constant d is referred to as the common difference. This is a first order linear recurrence relation. Traditionally, U 1 is represented by the letter a: U 1 = a. This can be proved by induction – LATER !!! The

a) Find the nth term b) The 10 th term of the arithmetic sequence 6, 11, 16, ……. .

b) Find the arithmetic sequence for which U 3 = 9 and U 7 = 17. Subtracting gives: Substituting gives:

c) Given the arithmetic sequence 2, 8, 14, 20, …. For what value of n is Un = 62?

Page 117 Exercise 2 A Questions TJ Exercise 1 Questions 1 to 3 1 a, c, d 2 a to e 3, 4, 6.

The Sum to n Terms on an Arithmetic Sequences Proof Adding

Find the sum of the first 15 terms of the arithmetic sequence which starts 3, 8, 13, 18, ……….

When does the sum of the arithmetic sequence which starts 2, 10, 18, 26, …. First exceed 300? We require Solving we get

The sum of the first four terms of an arithmetic sequence is 26. The sum of the first twelve terms is 222. What is the sum of the first 20 terms? NOTE

Page 120 Exercise 3 A Questions 1, 3, 4, 5 and 8 TJ Exercise 1 Questions 4 to 9

Geometric Sequences If a sequence is generated so that for all then the sequence is known as a geometric sequence. The constant r is referred to as the common ratio. The nth term:

a) Find the nth term and the 10 th term of the geometric sequence 3, 12, 48, ……. b) Find the geometric sequence whose 3 rd term is 18 and whose 8 th term is 4374 Substituting gives

c) Given the geometric sequence 5, 10, 20, 40, …… find the value of n for which

Page 123 Exercise 4 A Questions 1 a - e, 2, 3, 5 and 7 TJ Exercise 2 A Questions 1 to 4

The Sum to n Terms of a Geometric Sequence PROOF Multiplying by r: Subtracting:

a) Find the sum to 6 terms of the geometric sequence whose first term is 6 and whose common ratio is 1. 5.

b) A geometric sequence starts 12, 15, 18. 75, …… What is the smallest value of n for which Sn>100?

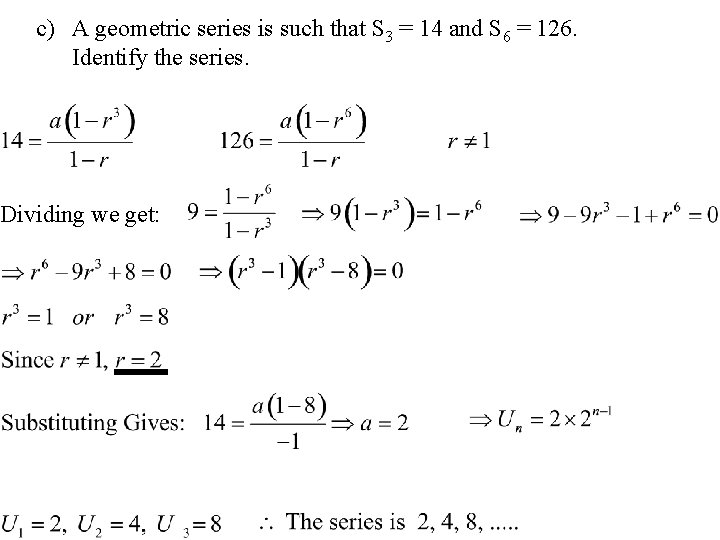
c) A geometric series is such that S 3 = 14 and S 6 = 126. Identify the series. Dividing we get:

Page 127 Exercise 5 a Questions 1, 2, 3, 4, TJ Exercise 2 A Questions 5 to 7

Infinite Series, Partial Sums, Sum to infinity. An Infinite series is a series which has an infinite number of terms. When we have an infinite series then Sn is defined as the sum to n terms of that series. Such a sum is referred to as a partial sum of the series. If the partial sum, Sn, tends towards a limit as n tends to infinity, then the limit is called the sum to infinity of the series.

Arithmetic Series The sum to infinity for an arithmetic series is undefined.

Geometric Series

a) Find the sum to infinity of the geometric series 24 + 12 + 6 + ……. . If it exists.

b) Express the recurring decimal 0. 121212…… as a vulgar fraction.

c) Given that 12 and 3 are two adjacent terms of an infinite geometric progression with find the first term. Hence the first term is 48.

Page 131 Exercise 6 A Questions 1 to 4 and 7 T. J. Exercise 2 B

Expanding (1 -x)-1 and Related Functions Remember:

This is a geometric series with first term 1 and common ration r.

Now Consider This is a geometric series with common ratio

a) Expand terms. in ascending powers of x giving the first four

b) Expand c) Evaluate giving the first four terms. to 4 decimal places.

d) Expand in ascending powers of x giving the first four terms

Page 134 Exercise 7 A Questions 2, 4. Page 134 Exercise 7 B Questions 2, 5. TJ Exercise 3

The Sequence and Limit of
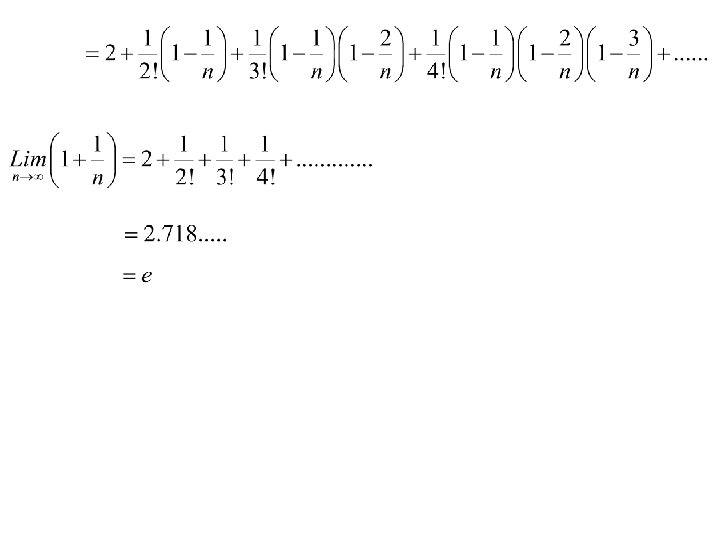

Summation of a Series The Sigma Notation The sigma notation is used as a more concise way of writing a series. e. g. 12 + 22 + 32 + 42 + 52 +…………+n 2 can be written more concisely as (i. e. the sum of all k 2 for k = 1 to k = n) In general is the series with the first term f(1), second term f(2), third term f(3) and last term f(n)
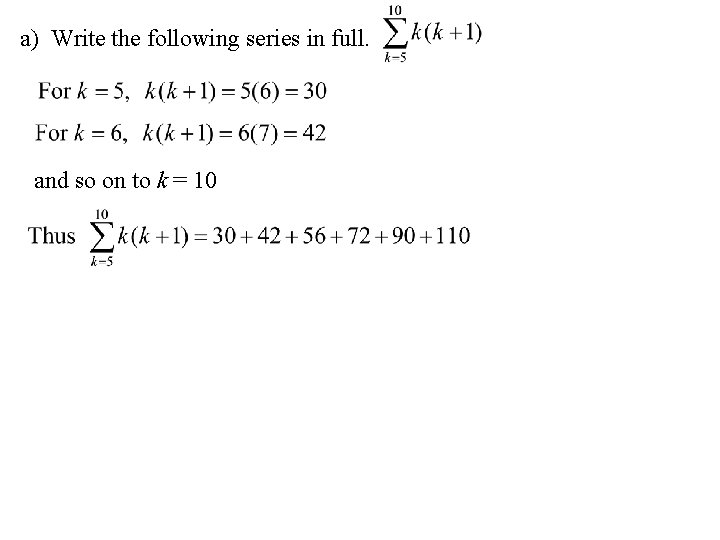
a) Write the following series in full. and so on to k = 10
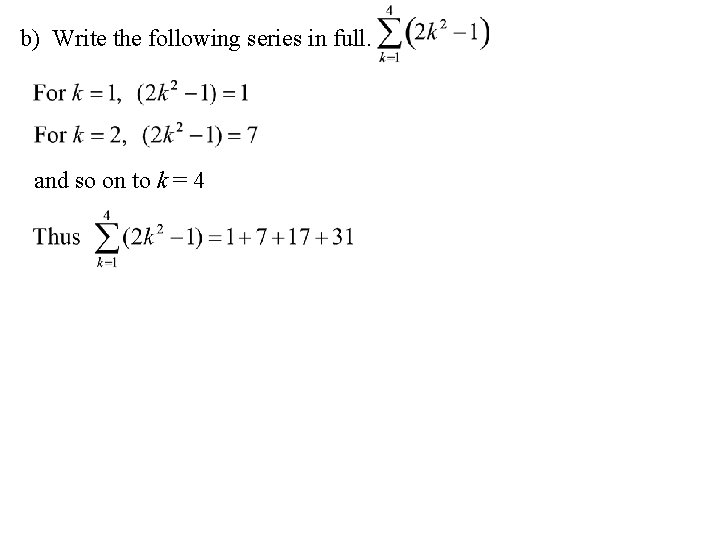
b) Write the following series in full. and so on to k = 4

c) Express the following in notation. 1+4+7+10+……. +298

Summation of a Series The sums of certain finite series can be found by a number of methods Proof: We can use this to help evaluate many summation series.
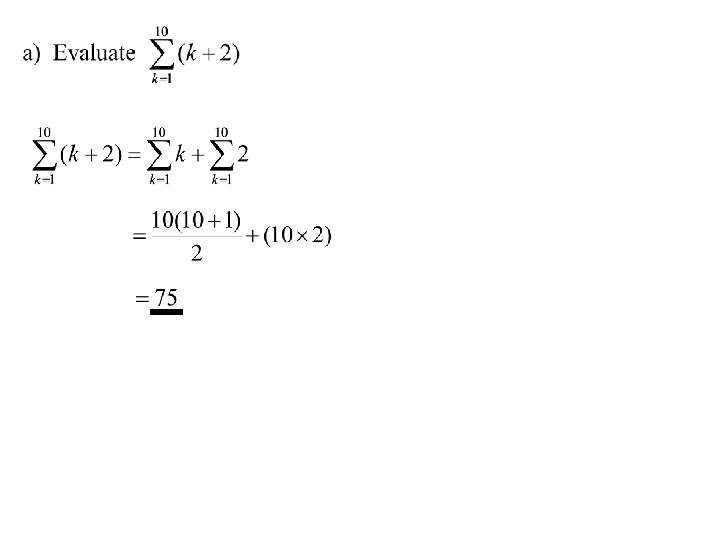


Page 137 Exercise 8 Questions 1 (a) to (d) 2 (a) to (b) and 4 TJ Exercise 4 and 5
 Arithmetic and geometric sequences and series
Arithmetic and geometric sequences and series A sequence is a list of ordered pairs.
A sequence is a list of ordered pairs. Unit 10 sequences and series homework 2 answers
Unit 10 sequences and series homework 2 answers Unit 10 sequences and series homework 1 answers
Unit 10 sequences and series homework 1 answers Chapter 12 sequences and series answers
Chapter 12 sequences and series answers 10-3 geometric sequences and series
10-3 geometric sequences and series Module 12 sequences and series
Module 12 sequences and series Explicit formula for geometric sequence
Explicit formula for geometric sequence 10-2 arithmetic sequences and series
10-2 arithmetic sequences and series 10-1 sequences series and sigma notation
10-1 sequences series and sigma notation 10-3 geometric sequences and series
10-3 geometric sequences and series Sequence and series formula
Sequence and series formula Sequences and series math 20-1
Sequences and series math 20-1 Chapter 1 sequences and series
Chapter 1 sequences and series Sequences and series math 20-1
Sequences and series math 20-1 Series and sequences
Series and sequences Sequences and series math 20-1
Sequences and series math 20-1 Sequences and series games
Sequences and series games What's arithmetic sequence
What's arithmetic sequence Sequences and series math 20-1
Sequences and series math 20-1 Series formula
Series formula Geometric sequence graphing calculator
Geometric sequence graphing calculator Dr frost sequences and series
Dr frost sequences and series 1/4^n convergence
1/4^n convergence Differentiate finite sequence from an infinite sequence
Differentiate finite sequence from an infinite sequence Nth term examples
Nth term examples Series and sequence examples
Series and sequence examples Series and sequence examples
Series and sequence examples Sum of geometric sequence
Sum of geometric sequence Difference between arithmetic series and sequence
Difference between arithmetic series and sequence Sequence and series cengage
Sequence and series cengage Series aiding and series opposing
Series aiding and series opposing Write domain and range in interval notation
Write domain and range in interval notation What is the domain of the set of ordered pairs
What is the domain of the set of ordered pairs Domain and range vocabulary
Domain and range vocabulary Python find pairs in list
Python find pairs in list Nucleotide sequence vs amino acid sequence
Nucleotide sequence vs amino acid sequence Pseudocode selection
Pseudocode selection Convolutional sequence to sequence learning
Convolutional sequence to sequence learning Series v sequence
Series v sequence Maclaurin series vs taylor series
Maclaurin series vs taylor series Heisenberg 1925 paper
Heisenberg 1925 paper Taylor vs maclaurin
Taylor vs maclaurin Deret maclaurin
Deret maclaurin Ibm p series servers
Ibm p series servers Amplifier feedback topologies
Amplifier feedback topologies Sum of infinite series formula
Sum of infinite series formula Ordered pairs that represent a function examples
Ordered pairs that represent a function examples Formula hipotenusa triangle rectangle
Formula hipotenusa triangle rectangle Reporting imperative sentences
Reporting imperative sentences Set of ordered pairs
Set of ordered pairs Entailment presupposition
Entailment presupposition









































































