Sequences and Series IB standard Students should know

Sequences and Series IB standard • Students should know Arithmetic sequence and series; sum of finite arithmetic series; geometric sequences and series; sum of finite geometric series

Arithmetic Sequence

Arithmetic Sequences • An arithmetic sequence is a sequence in which each term differs from the pervious one by the same fixed number • Example – 2, 5, 8, 11, 14 • 5 -2=8 -5=11 -8=14 -11 etc – 31, 27, 23, 19 • 27 -31=23 -27=19 -23 etc

Algebraic Definition • {an} is arithmetic an+1 – an= d for all positive integers n where d is a constant (the common difference) – “If and only if” – {an} is arithmetic then an+1 – an is a constant and if an+1 – an is constant the {an} is arithmetic

The General Formula • a 1 is the 1 st term of an arithmetic sequence and the common difference is d • Then a 2 = a 1 + d therefore a 3 = a 1 + 2 d therefore a 4 = a 1 + 3 d etc. • Then an = a 1 + (n-1)d the coefficient of d is one less than the subscript

No common difference! Arithmetic Sequence

Example #1 • Consider the sequence 2, 9, 16, 23, 30… – Show that the sequence is arithmetic – Find the formula for the general term Un – Find the 100 th term of the sequence – Is 828, 2341 a member of the sequence?

Geometric Sequence

Arithmetic Sequences Geometric Sequences • ADD To get next term • MULTIPLY to get next term • Have a common difference • Have a common ratio

In a geometric sequence, the ratio of any term to the previous term is constant. You keep multiplying by the SAME number each time to get the sequence. This same number is called the common ratio and is denoted by r What is the difference between an arithmetic sequence and a geometric sequence? Try to think of some geometric sequences on your own!

No common ratio! Geometric Sequence

To write a rule for the nth term of a geometric sequence, use the formula:

Write a rule for the nth term of the sequence 6, 24, 96, 384, . . Then find This is the general rule. It’s a formula to use to find any term of this sequence. To find , plug 7 in for n.

Write a rule for the nth term of the sequence 1, 6, 36, 216, 1296, . . Then find This is the general rule. It’s a formula to use to find any term of this sequence. To find , plug 8 in for n.

Write a rule for the nth term of the sequence 7, 14, 28, 56, 128, . . Then find

One term of a geometric sequence is = 3. Write a rule for the nth term. The common ratio is r

One term of a geometric sequence is and one term is Step 1: Find r -divide BIG small -find the distance between the two terms and take that root. Step 2: Find. Plug r, n, and equation. Then, solve for. into your Step 3: Write the equation using r and .

Write the rule when and .

Series and Sequences Formulas

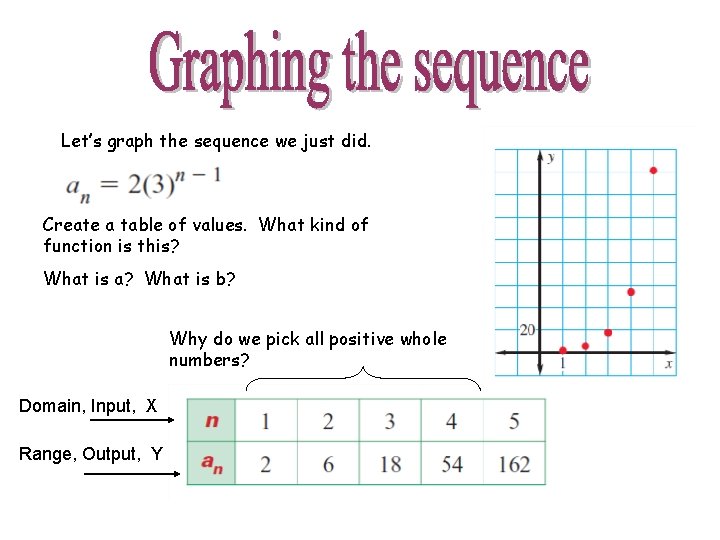
Let’s graph the sequence we just did. Create a table of values. What kind of function is this? What is a? What is b? Why do we pick all positive whole numbers? Domain, Input, X Range, Output, Y

Compound Interest Formula • P dollars invested at an annual rate r, compounded n times per year, has a value of F dollars after t years. • Think of P as the present value, and F as the future value of the deposit.

Compound Interest • So if we invested $5000 that was compounded quarterly, at the end of a year looks like: • After 10 years, we have:

Series and Sequences Formulas