GCSE Linear Sequences Dr J Frost jfrosttiffin kingston






- Slides: 7

GCSE: Linear Sequences Dr J Frost (jfrost@tiffin. kingston. sch. uk) Last modified: 19 th January 2013

Recap: Formula for nth term Either find the formula for the nth term, or given the formula, find the first few terms of the formula. First 5 terms in sequence Formula for nth term. 3, 5, 7, 9, 11, . . . 2 n + 1 1, 4, 7, 10, 13, ? . . . 3 n – 2 7, 12, 17, 22, 27, . . . 5 n + 2 9, 7, 5, 3, 1, ? . . . -2 n + 11 1, -3, -7, -11, -15, . . . -4 n + 5 ? 100 th term 201 298 ? 502 -189 ? -395 ? ? ?

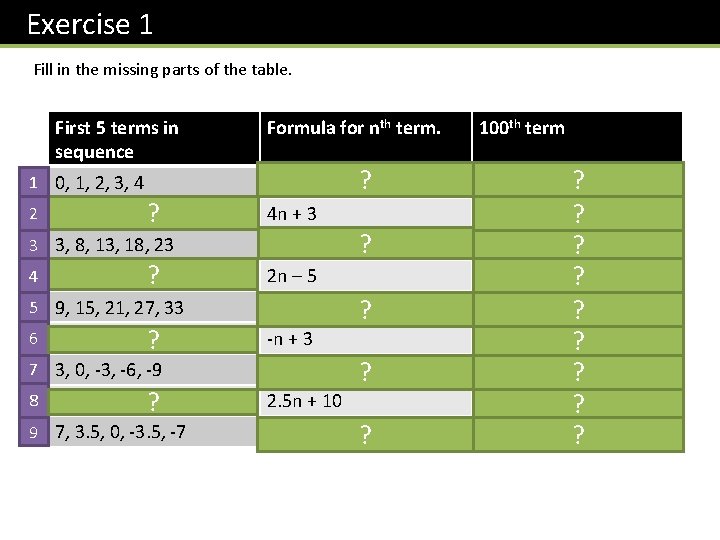
Exercise 1 Fill in the missing parts of the table. First 5 terms in sequence Formula for nth term. 1 0, 1, 2, 3, 4 n– 1 2 7, 11, 15, 19, ? 23 4 n + 3 3 3, 8, 13, 18, 23 5 n – 2 4 -3, -1, 1, 3, 5 ? 2 n – 5 5 9, 15, 21, 27, 33 6 n + 3 6 2, 1, 0, -1, -2 ? -n + 3 7 3, 0, -3, -6, -9 -3 n + 6 8 12. 5, 17. 5, ? 20, 22. 5 n + 10 9 7, 3. 5, 0, -3. 5, -7 ? 100 th term 99 403 ? 498 195 ? 603 ? -294 -3. 5 n + 10. 5? -97 260 -339. 5 ? ? ? ? ?

Interpreting Sequences There are often follow up questions which require more than just computing a given term of the sequence or the formula for the nth term. Q 3, 7, 11, 15, 19, . . . Jasmine argues that 204 is in the sequence. Is she right? No, because 204 is an even number, and the sequence contains only odd ? numbers. Q 4, 7, 10, 13, 16, . . . Tarquin argues that 3002 is in the sequence. Is he right? No, because 3002 is two more than a multiple of 3, whereas the numbers ? in the sequence are 1 more than a multiple of 3.

Difficult Sequences Question (From a GCSE specimen paper) Q 1, 4, 7, 10, . . . a) Find an expression for the nth term of the sequence. 3 n – 2 b) Sophie claims that when she squares any term in the sequence, she gets a term that is in the same sequence. Show that she is right. (3 n – 2)2 = 9 n 2 – 12 n + 4 = 9 n 2 – 12 n + 6 – 2 = 3(3 n 2 – 4 n + 2) – 2 ? minus 2”, so must be in the This is in the form “ 3 times an integer sequence. The approach amounts to squaring the formula for the nth term, and showing (by rearranging) that this can written in the same form (i. e. three times something minus 2).

Difficult Sequences Question Now your turn. . . Q 7, 13, 19, 25, 31, . . . a) Find an expression for the nth term of the sequence. 6 n + 1 ? b) Bob claims that when he squares any term in the sequence, he gets a term that is in the same sequence. Show that he is right. (6 n + 1)2 = 36 n 2 + 12 n + 1 = 6(6 n 2 + 2 n) + 1 This is one more than a multiple of? 6, so must be in the sequence.

Exercise 2 For the following, justify why the given term is not in the sequence. 1 Sequence Term a 4, 6, 8, 10, . . . 1351 b Sequence contains only even terms, while 1351 is odd. 11, 16, 21, 26, 31, . . . 1543 All the terms in the sequence end with 1 or 6. c 7, 10, 13, 16, . . . 302 Terms in sequence are one more than a multiple of 3, whereas 302 is two more. d 2, 6, 10, 14, . . . 424 e 5, 12, 19, 26, . . . ? ? Prove algebraically that the following actions to any term in the sequence gives a term still in the sequence. 2 a 5, 9, 13, 17, . . . Squaring (4 n + 1)2 = 16 n 2 + 8 n + 1 = 4(n 2 + 2 n) + 1 b 1, 6, 11, 16, . . . Adding 15. (5 n – 4) + 15 = 5 n + 11 = 5 n + 15 – 4 = 5(n + 3) – 4 c 1, 7, 13, 19, 25, . . . Squaring (6 n – 5)2 = 36 n 2 – 60 n + 25 = 36 n 2 – 60 n + 30 – 5 = 6(6 n 2 – 10 n + 10) - 5 ? 1856 Terms in sequence are two more than a multiple of 4, whereas 424 is a multiple of 4. ? Terms in sequence are 5 more than a multiple of 7, whereas 1856 is one more. ?