Sequences and series 1 sequences 1 An ordered












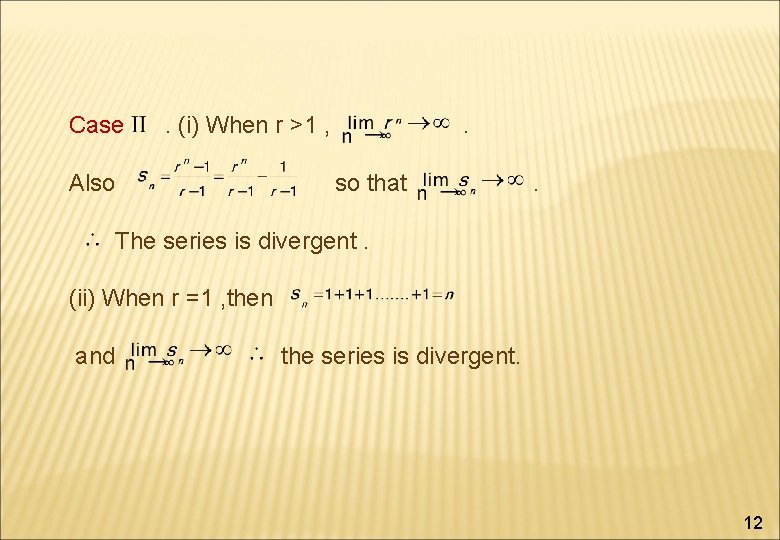
















































- Slides: 61

Sequences and series

1. sequences (1) An ordered set of real numbers called a sequence and is denoted by ( is ). If the number of terms is unlimited , then the sequence is said to be an infinite sequence and is its general term. For instance (i) 1, 3, 5, 7, …, (2 n-1), …, 1

(ii) 1, 1/2, 1/3, …, 1/n, . . . , (iii) 1, -1, …, (-1) , … are infinite sequences. (2) Limit. A sequence is said to tend to a limit a value N of n can be found such that We then write or simply , if for every ε >0 , for n ≥ N. as 2

(3) Convergence. If a sequence ( ) has a finite limit, it is called a convergent sequence. If ( ) is not convergent, it is said to be divergent. In the above examples , (ii) is convergent, while (i) and (iii) are divergent. 3

(4) Bounded sequence. A sequence ( , if there exists a number ) is said to be bounded such that (5) Monotonic sequence. the sequence ( for every n. ) is said to increase steadily or to decrease steadily according as for all values of or . 4

Both increasing and decreasing sequences are called monotonic sequences. A monotonic sequence always tends to alimit , finite or infinite. Thus, a sequence which is monotonic and bounded is convergent. 5

2. series (1) Def. if be an infinite sequence of real numbers , then Is called an infinite series. An infinite series is denoted by and the sum of its first terms is denoted by . 6

(2) Convergence, divergence and oscillation of a series. Consider the infinite series And let the sum of the first Clearly , is a function of terms be and as increases indefinitely three possibilities arise. 7

(i) If tends to a finite limit as , the series is said to be convergent. (ii) If tends to as , the series is said to be divergent. (iii) If does not tend to a unique limit as the series , then is said to be oscillatory or non-convergent. 8

Example 2. 1 Examine for convergence the series. sol . Here Hence this series is divergent. Example 2. 2 Test the convergence of the series. sol . Here terms 9

=0, 5 or 1 according as the number of terms is 3 m, 3 m+1, 3 m+2. clearly in this case, does not tend to a unique limit. Hence the series is oscillatory. Example 2. 3 Geometric series Show that the series (i) Converges if (iii) oscillates if , (ii) diverges if , and . 10

sol. Let Case Also . When . so that The series is convergent. 11
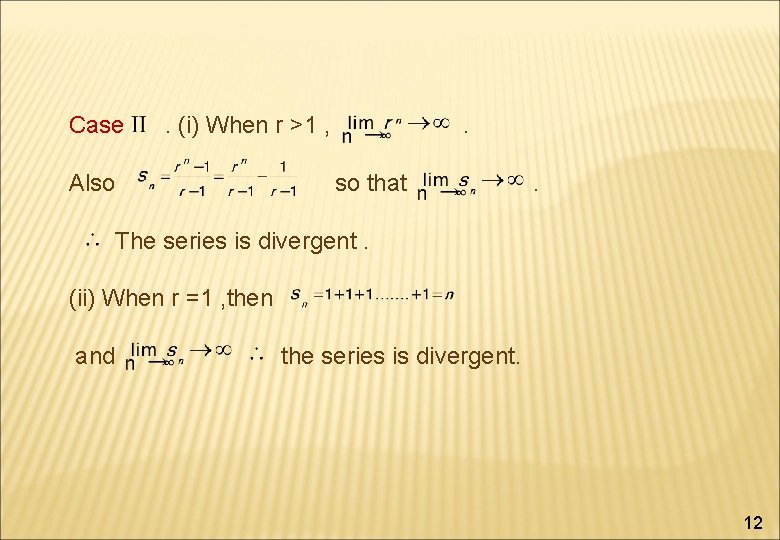
Case . (i) When r >1 , Also . so that . The series is divergent. (ii) When r =1 , then and the series is divergent. 12

Case . (i) When r =-1 , then the series becomes 1 -1+1 -1…. which is an oscillatory series. . (ii) When r < -1 , let r = -p so that p >1 Then and as . according as n is even or odd. Hence the series oscillates. 13

3. GENERAL PROPERITIES OF SERIES The truth of the following properties is self –evident and these may be regarded as axioms : 1. The convergence or divergence of an infinite series remains unaffected by the addition or removal of a finite number of its terms ; for the sum of these terms being 14

the finite quantity does not on addition or removal alter the nature of its sum. 2. If a series in which all the terms are positive is convergent , the series remains convergent even when some or all of its terms are negative ; for the sum is clearly the greatest when all the terms are positive. 15

3. The convergence or divergence of an infinite series remains unaffected by multiplying each term by a finite number. 4. Series of positive terms 1. An infinite series in which all the terms after some particular term are positive term series. 16

e. g. , -7 -5 -2+2+7+13+20+……is a positive term series as all its terms after the third are positive. 2. A series of positive terms either converges or diverges to + ; for the sum of its first n terms , omitting the negative terms , tends to either a finite limit or + . 17

3. Necessary condition for convergence. If a positive term series Let is convergent , then since is given to be convergent. finite quantity k (say). Also But Hence the result. 18

Obs. 1. It is important to note that the converse of this result is not true. Consider, for instance , the series Since the term go on descending , i. e. 19

Thus the series is divergent even though Hence is a necessary but not sufficient condition for convergence of . Obs. 2. The above result leads to a simple test for divergence : If , the series must be divergent. 20

5. COMPARISON TESTS If two positive term series (i) converges , and (ii) be such that for all values of n , then also converges. Proof. Since is convergent , 21

a finite quantity k (say) Also since Adding, Hence the series also converges. 22

Obs. If , however , the relation holds for values of n greater than a fixed number m , then the first m terms of both the series can be ignored without affecting their convergence or divergence. II. If two positive term series and be such that : 23

(i) diverges , (ii) for all values of n , then also diverges. Its proof is similar to that of Test I. III. Limit form If two positive term series finite quantity ( and ) , then be such that and converge or diverge together. 24

Proof. Since , a finite number ( ) By definition of a limit , there exists a positive number , however small , such that for or for 25

Omitting the first m terms of both the series , we have for all n Case I When is convergent, then a finite number Also from (1) , …. . (1) i. e. …. . (2) for all n. by (2) 26

Hence is also convergent. Case II. When is divergent , then …. (3) Also from (1) or for all n [by (3) Hence is also divergent. 27

6. INTEGRAL TEST A positive term series f(1)+f(2)+……+f(n)+…. . , where f(n) decreases as n increases , converges or diverges according as the integral is finite or infinite. 28

The area under the curve y=f(x), between any two ordinates lies between the set of inscribed and escribed rectangles formed by ordinates at x=1, 2, 3, …… as in Fig 6. 1 Then 29

Fig 6. 1 Taking limits as , we find from the second inequality that limit 30

Hence if integral (1) is finite , so is limit . Similarly , from the first inequality , we see that if the integral (1) is infinite , so is limit diverges to + . But the given series either converges or , i. e. limit either finite or infinite Hence the result follows. 31

Example 6. 1 show that the harmonic series of order p i. e. for p sol Converges for p>1 and diverges 1. By the above test , this series will converge or diverge according as is finite or infinite. 32

If p 1, , i. e. finite for p>1 for p<1 If p=1, , this proves the result. 33

Example. 6. 2 test for convergence the series sol. We have Take Then =2 , which is finite and non –zero. 34

Both But Hence and converge or diverge together. is known to be convergent. is also convergent. Example 6. 3 Test the convergence of the series : (i) (ii) 35

sol. (i) We have (Expanding by Binomial Theorem) Taking , We have which is finit and non zero. 36

Both But and converge or diverge together. is known to be divergent. Hence is also divergent. (ii) When x<1, comparing the given series with , We get [ 37

But is convergent , so When x>1, comparing But is convergent, so When x=1, Hence , is also convergent. with , we get is also convergent. Which is divergent. converges for x<1 and x>1 but diverges for x=1. 38

7. COMPARISON OF RATIOS If if (i) and be two positive term series , then converges , and (ii) from and after some particular term, 8. D’ALEMBERT’S RATIO TEST In a positive term series converges for if and diverges for , then the series. 39

Example 8. 1 Test for convergence the series (i) (ii) sol. (i)We have and 40

= . Hence and diverges if If converges if . , then , Taking Both , we get and , afinite quantity. converge or diverge together. But is a convergent series. 41

is also convergent. Hence the given series converges if and diverges if . (ii) Here Thus by Ratio test, converges for x<1 and diverges for x>1. But it fail for x=1. 42

When x=1, diverges for x=1. Hence the given series converges for x<1 and diverges for x Example 8. 3 (i) 1. Discuss the convergence of the series (ii) 43

sol. (i) We have Hence the given series is convergent. (ii) Given series is Hence the given series is convergent. 44

9. ALTERNATING SERIES (1) Def. A series in which the terms are alternately positive or negative is called an alternating series. (2) Leibnitz’s rule*. An alternating series converges if (i) each term is numerically less than its preceding term, and (ii) 45

If , the given series is oscillatory. The given series is Suppose …(1) and …(2) Consider the sum of 2 n terms. It can be written as …(3) or as …(4) 46

By virtue of (1), the expressions within the brackets in (3) and (4) are all positive. It follows from (3) that Also from (4), We note that Hence is positive and increases with n. always remains less than . must tend to a finite limit. 47

Moreover Thus [by (2) tends to the same finite limit whether n is even or odd. Hence the given series is convergent. When The given series is oscillatory. 48

Example 9. 1 (i) sol Discuss the convergence of the series (ii) (i) The terms of the given series are alternately positive and negative ; each term is numerically less than its preceding term 49

Also Hence by Leibnitz’s rule, the given series is convergent. (ii) The terms of the given series are alternately positive and negative and i. e. Also Hence by Leibnitz’s rule , the given series is oscillatory. 50

Example 9. 2 (i) sol Examine the character of the series (ii) (i) The terms of the given series are alternately positive and negative ; and each term is numerically less than its preceding term. 51

But which is not zero. Hence the given series is oscillatory. (ii) The terms of the given series are alternately positive and negative i. e. , Also Hence the given series is convergent. 52

10. SERIES OF POSITIVE OR NEGATIVE TERMS The series of positive terms and the alternating series are special types of these series with arbitrary signs. Def. (1) If the series of arbitrary terms be such that the series is convergent, then the series is said to be absolutely convergent. 53

(2) If is divergent but is convergent, then is said to be conditionally convergent. For instance, the series is absolutely convergent, since the series is known to be convergent. 54

Again , since the alternating series is convergent, and the series of absolute values is divergent, so the original series is conditionally convergent. 55

Example 10. 1 Test whether the series is convergent or not ? sol The series of absolute terms is which is, evidently convergent. The given series is absolutely convergent and hence it is convergent. 56

Example 10. 2 Test for convergence and absolute convergence. sol The terms of the given series are alternately positive or negative. Also each term is numerically less than the preceding term and 57

Hence, the given series is convergent by Leibnitz’s rule. Also which is a finite quantity. Thus the given series is absolutely convergent. Example 10. 3 Test the series for conditional convergence 58

sol Here Then i. e. Also Thus by Leibnitz’s rule, and therefore is convergent. 59

Also Since i. e. . Taking we note that is divergent, therefore Is convergent but Thus the given series is also divergent. is divergent. is conditionally convergent. 60
 Arithmetic and geometric sequences and series
Arithmetic and geometric sequences and series Unit 10 sequences and series homework 1 answers
Unit 10 sequences and series homework 1 answers Unit 10 sequences and series
Unit 10 sequences and series Chapter 12 sequences and series answers
Chapter 12 sequences and series answers 10-3 geometric sequences and series
10-3 geometric sequences and series Module 12 sequences and series answers
Module 12 sequences and series answers Geometric series formula
Geometric series formula 10-2 practice arithmetic sequences and series
10-2 practice arithmetic sequences and series 10-1 sequences series and sigma notation
10-1 sequences series and sigma notation Sum of gp formula
Sum of gp formula Sequences and series formulas
Sequences and series formulas Math 20-1 sequences and series
Math 20-1 sequences and series Chapter 1 sequences and series
Chapter 1 sequences and series Sequences and series math 20-1
Sequences and series math 20-1 Sequence and series
Sequence and series Math 20-1 sequences and series
Math 20-1 sequences and series Sequences and series games
Sequences and series games How do you find d in arithmetic sequence
How do you find d in arithmetic sequence Sequences and series math 20-1
Sequences and series math 20-1 Sequences and series
Sequences and series Sequences and series precalculus
Sequences and series precalculus Dr frost sequences
Dr frost sequences 9 + 1 = 10
9 + 1 = 10 Series aiding and series opposing
Series aiding and series opposing Give the domain
Give the domain What is the domain of the set of ordered pairs
What is the domain of the set of ordered pairs Range of relation
Range of relation Python find pairs in list
Python find pairs in list Maclaurin series vs taylor series
Maclaurin series vs taylor series Balmer series lyman series
Balmer series lyman series Taylor series of composite functions
Taylor series of composite functions Taylor vs maclaurin
Taylor vs maclaurin Ibm p series server
Ibm p series server In current series feedback topology mixing is
In current series feedback topology mixing is Arithmetic series vs geometric series
Arithmetic series vs geometric series Ordered pairs that represent a function examples
Ordered pairs that represent a function examples The pythagorean theorem
The pythagorean theorem Reported commands examples
Reported commands examples Set of ordered pairs
Set of ordered pairs Ordered entailment in pragmatics
Ordered entailment in pragmatics An ordered arrangement
An ordered arrangement Partially ordered tree
Partially ordered tree Which ordered pair is a solution of the equation
Which ordered pair is a solution of the equation Polygon filling algorithm in computer graphics
Polygon filling algorithm in computer graphics Partially ordered tree
Partially ordered tree Ordered pair in algebra
Ordered pair in algebra Binary tree descendants
Binary tree descendants Adverb complex
Adverb complex A sequence is a list of ordered pairs.
A sequence is a list of ordered pairs. Ordered broadcast
Ordered broadcast What is ordered broadcasts?
What is ordered broadcasts? Tora algorithm
Tora algorithm A sports company was ordered to prepare 100 paper cylinders
A sports company was ordered to prepare 100 paper cylinders Eva has ordered eight 6 digit numbers
Eva has ordered eight 6 digit numbers These were assaults ordered by attorney general mitchell
These were assaults ordered by attorney general mitchell An ordered arrangement
An ordered arrangement Order of events
Order of events B tree order 3
B tree order 3 An ordered life
An ordered life Queue/ antraian = ordered list
Queue/ antraian = ordered list Ordered pair
Ordered pair Product rule for ordered pairs
Product rule for ordered pairs