A 1 SEQUENCES A sequence is an ordered












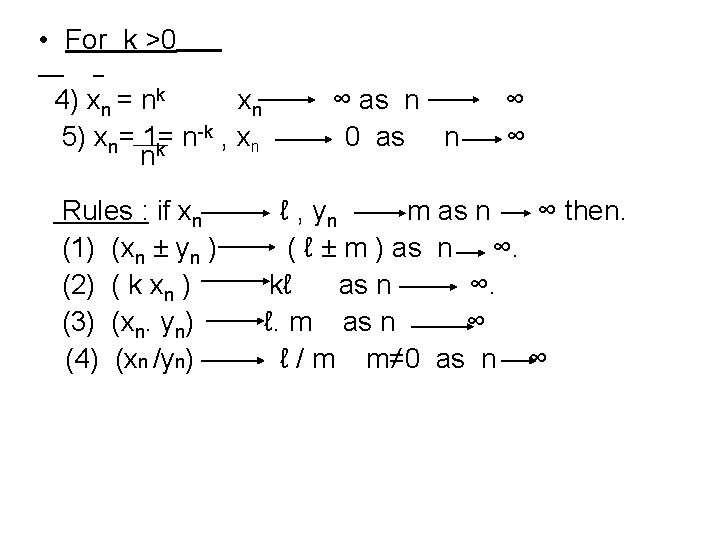



- Slides: 17


A 1: SEQUENCES • A sequence is an ordered list of numbersfinite or infinite-called terms. • Notation: The nth term of a sequence is denoted by an. The subscript or suffix n indicates its position. The sequence itself is either denoted by a or (an). • Ex 1: a=(an)=(1, 4, 9, 16, 25): finite • Ex 2: b=(bn)=(1, 3, 5, 7, 9, …) infinite • Ex 3: c=(cn)=(3, -2, 2, 3, 2, 1)

Graph of a sequence: plotted by taking ordered pairs (n, an) for n in the domain of definition an . . n 1 2 3 4

• Describing sequences: • A closed form of a sequence is a rule or formula giving nth term an in term of n. • Eg in Ex 1: an=n 2, n=1, 2, 3, 4, 5… perfect squares. in Ex 2: bn=2 n+1, n=0, 1, 2, 3, … Or bn=2 n-1 n=1, 2, 3 odd numbers. • Convention: first term is usually taken as a 1(starting from n=1). • Sometimes we start from n=0, i. e. first term in a 0.

Examples: dn=1/n(n-1), n=2, 3, … un=(-1)n 1/n, n=1, 2, 3, …. • A recurrence relation: gives any term of the sequence in terms of the preceding term. (a first order recurrence relation). e. g. in Ex 2: bn=bn-1+2, n=1, 2, 3, … A recurrence system consists of a recurrence relation, the first term and an index range.

• Arithmetic sequences: are sequences where the difference between any two consecutive terms is constant-called the common difference and denoted by d. (Also called arithmetic progression) Example: Ex 2: bn=bn-1+2, here d=2.

• Arithmetic sequence: with first term a and difference d is given by the recurrence system: x 1=a, xn+1= xn+d, n=1, 2, 3…. • Parameters of the sequence are its first term a and difference d. • Closed from of an arithmetic sequence is • x 1=a, xn=a+(n-1)d, n=1, 2, 3… or alternatively x 0 =a, xn=a+nd, n=0, 1, 2… 7

• GEOMETRIC SEQUENCES: are sequence where the ratio between any two consecutive terms is constant- called the common ratio and denoted by r, (also called geometric progression). • Parameters are: first term a, common ratio r • Recurrence relation: x 1=a, xn+1=rxn, n=1, 2, 3, . . Or x 0=a, xn+1=rxn, n=0, 1, 2, . .

Example: xn+1=2 xn, n=1, 2, … If x 1=2 If x 1=3 (xn)=(2, 4, 8, 16…) (xn)=(3, 6, 12, 24, . . ) Closed from of a geometric sequence: x 1 =a, xn =arn-1 , n=1, 2, 3, … OR x 0=a, xn=arn, n=0, 1, 2, 3, …

• Sum Sn of first n terms of the geometric sequence xn=rn and first term =1: Sn= 1+r+r 2+…+rn-1. rsn= r+r 2+. . +rn-1+rn rsn—Sn=Sn(r-1)= rn-1 : . Sn = (rn-1 )/(r-1) or (1 -rn ) /(1 -r) , r≠ 1

• Linear Recurrence Sequences : each term is given as a linear function of the preceding term. • xn+1 = r xn +d , r , d constants , n = 1, 2, 3, … • Parameters are : first term a , ratio r and difference d.

• They generalize both arithmetic sequences and geometric sequence (special cases ). • (1) r =1 xn+1 =xn+d (arithmetic sequence ) (2) d = 0 xn+1 = rxn (geometric sequence). • Recurrence system : x 1 = a , xn+1 = rxn +d , n = 1, 2, 3, … or x 0 = a , xn+1 = rxn +d , n = 0, 1, 2, 3, . . • Closed form is x 1 = a , xn = (a+ d/(r-1) ) rn-1 – d/(r-1) , n=1, 2, 3, … or x 0 = a , xn = (a+ d/(r-1) ) rn – d/(r-1), n=0, 1, 2…

• Long term behaviour of sequences : For a sequence xn : as n → ∞ if xn → ℓ(i. e. xn become arbitrarily close to ℓ ) then we describe the long term ( or long run ) behaviour of the sequence by : xn → ℓ as n → ∞. equivalently written lim xn =ℓ. n ∞ Examples : 1) xn = k , constant : xn → k as n → ∞ 2) xn = 1/n , xn → 0 as n → ∞ 3) xn = n , xn → ∞ as n→ ∞
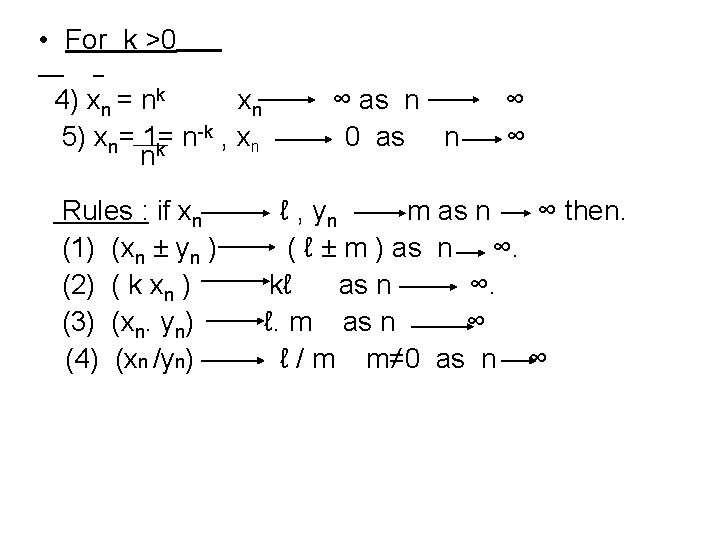
• For k >0 4) xn = nk xn -k , x 5) xn= 1= n n nk Rules : if xn (1) (xn ± yn ) (2) ( k xn ) (3) (xn. yn) (4) (xn /yn) ∞ as n 0 as n ∞ ∞ ℓ , yn m as n ∞ then. ( ℓ ± m ) as n ∞. kℓ as n ∞. ℓ. m as n ∞ ℓ / m m≠ 0 as n ∞

• • Examples : if an in a rational function of n: write an=P /Q , P, Q polynomials in n. I If degree(P) > degree(Q) then an →∞ as n→∞ II If degree (P) < degree (Q) then an → 0 as n→∞ III If degree (P)= degree (Q) then an → coefficient of highest power in P÷ coefficient of highest power in Q as n → ∞

Long term behaviour of rn : (Table) Range of r r >1 r=1 -1 < r < 1 Behaviour of rn rn →∞ as n →∞ rn → 1 as n→∞ rn → 0 as n →∞ r = -1 rn alternates between as n →∞ 1 and-1 , r < -1 rn is unbounded and alternates in sign as n→∞

A special limit • an=(1+1/n)n→e ~ 2. 718. . as n →∞. • bn = (1+x/n)n → ex as n →∞. Examble : ( 1 - 5/n )n → e-5 as n →∞ • Sequences and Models : (A 1 pp 36 -38 ) • Used Arithmetic sequence to model the book and oil sequences. • Used Geometric sequence to model the saving account and bouncing ball sequences. • Used linear recurrence sequence to model the deer population and mortgage sequences.