UNIT 5 RELATIONS FUNCTIONS AND GRAPHING FUNCTIONS A



































- Slides: 50

UNIT 5 RELATIONS, FUNCTIONS, AND GRAPHING

FUNCTIONS • A relation is a set of ordered pairs. For example: {(3, 2), (4, 5), (6, 8), (7, 1)} • The relation can represent a finite set of ordered pairs or an infinite set.

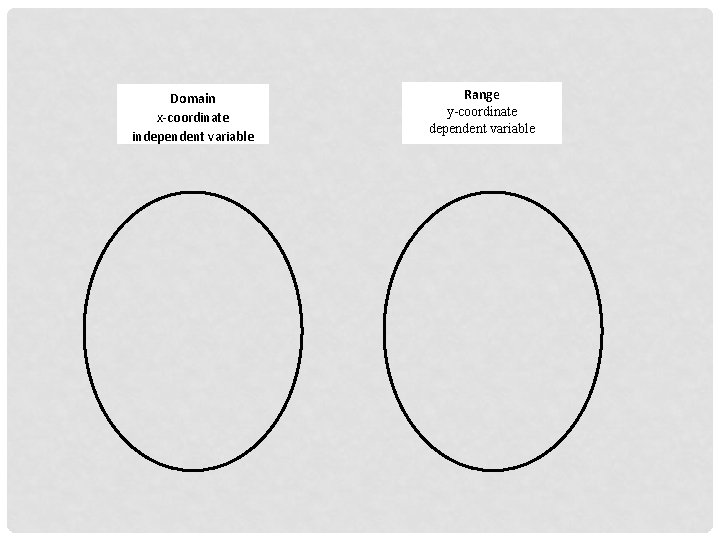
Domain x-coordinate independent variable Range y-coordinate dependent variable

• The domain of a relation is the set of all xcoordinates from the ordered pairs in a relation. • The range of a relation is the set of all ycoordinates from the ordered pairs in a relation.

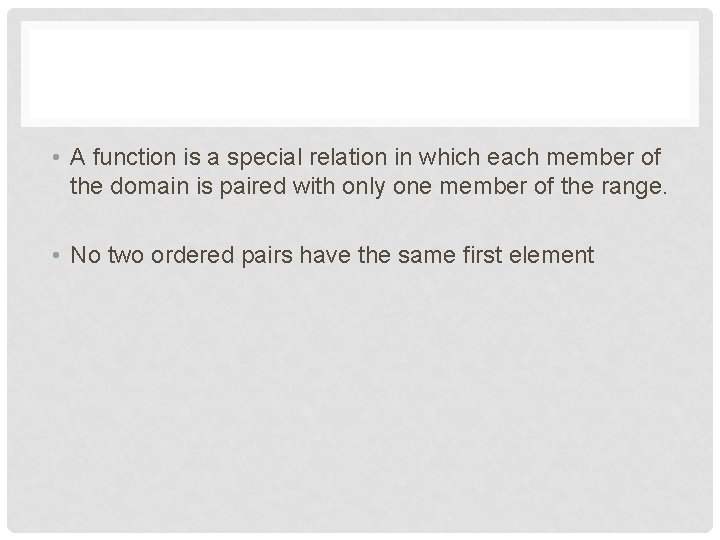
• A function is a special relation in which each member of the domain is paired with only one member of the range. • No two ordered pairs have the same first element

EXAMPLES • Determine whether each set of ordered pairs represents a function • {(3, 2), (4, 5), (6, 8), (7, 1)} • {(0, 5), (4, 3), (6, 5), (-7, -4)} • {(1, 3), (4, 2), (4, 1), (5, 6)} • {(6, -2), (11, -3), (14, 9), (-14, 11), (-14, 20), (21, -21)} • x 5 3 2 1 0 -4 -6 y 1 3 -2 2 -2

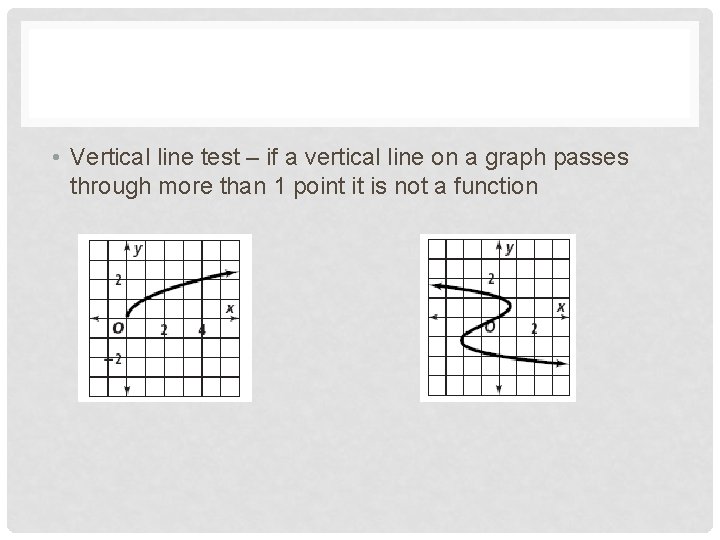
• Vertical line test – if a vertical line on a graph passes through more than 1 point it is not a function

• A solution to an equation or inequality in two variables is an ordered pair (x, y) that makes the equation or inequality true.

EXAMPLES – 3 x + 6 y = 12 (-4, 0) x + 5 y ≥ 11 (2, 1) 3 y – 5 x = 4 (-2, -2) 5 y < 3 x (-1, -3)

GRAPHING LINEAR FUNCTIONS Linear Equations • • Equations whose graphs are a straight line Find five values for the domain and make a table Plot each ordered pair Draw a straight line through the points Label the line with the original equation

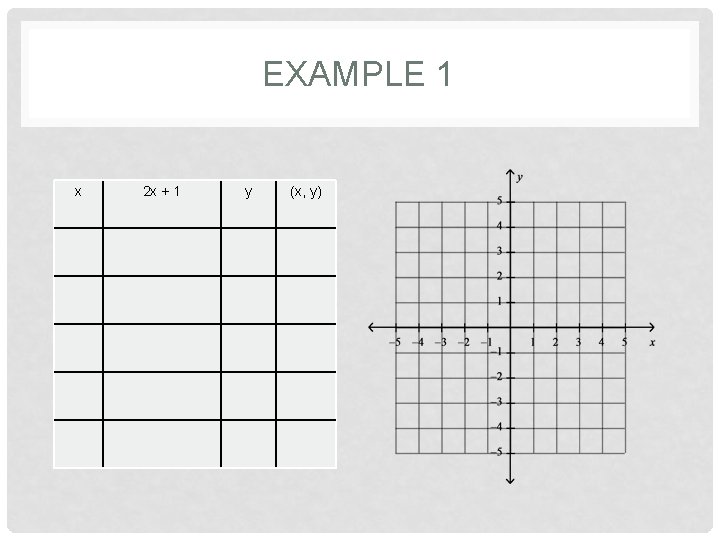
EXAMPLE 1 x 2 x + 1 y (x, y)

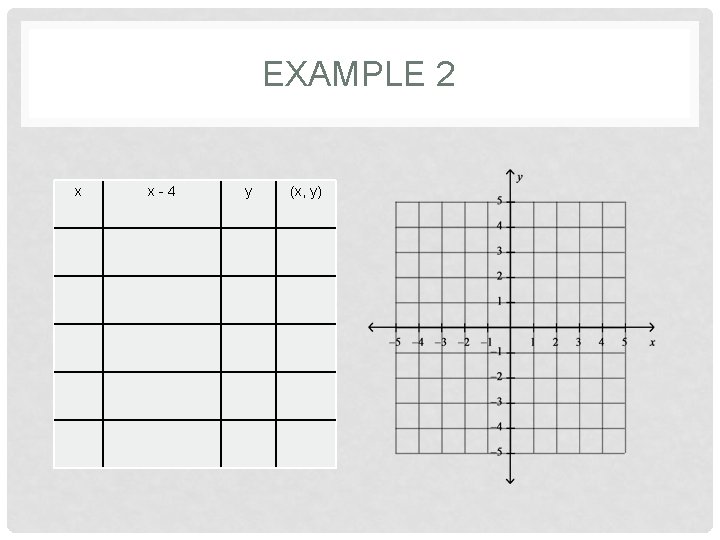
EXAMPLE 2 x x - 4 y (x, y)

Standard Form of a Linear Equation where A, B, and C are real numbers, and A and B cannot both be zero.

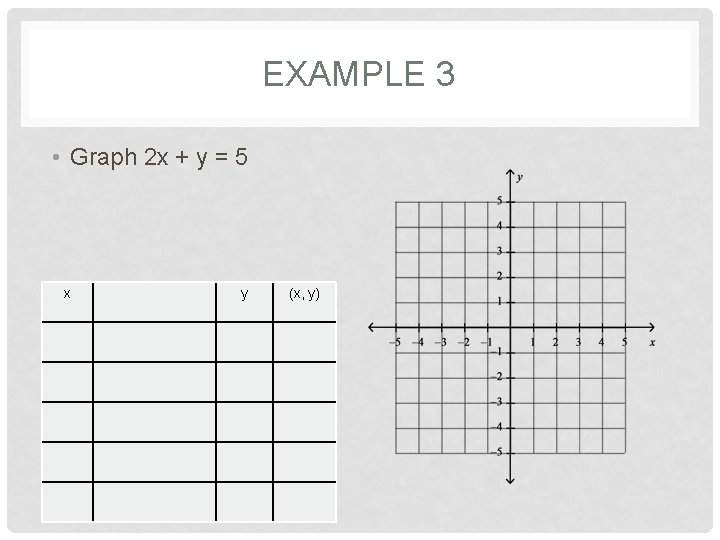
EXAMPLE 3 • Graph 2 x + y = 5 x y (x, y)

WARM-UP •

HORIZONTAL & VERTICAL LINES y = c A _________ line parallel to the _____axis. x = c A ________line parallel to the____-axis. The y-coordinate has the The x-coordinate has the same value.

EXAMPLES

The cost of renting a car for a day is $64. 00 plus $0. 25 per mile. Let x represent the number of miles the car was driven and let y represent the rental cost, in dollars, for a day. a. Write an equation for the rental cost of the car in terms of the number of miles driven. b. Graph the equation


EXAMPLES • What must be the value of k be if (k, 4) lies on the line 3 x + y = 10? • What must the value of k be if (5, -3) lies on the line y – x = k • Find k such that (k, 5) is a solution of 3 x + 2 y = 22

SLOPE OF A LINE • Slope measures the steepness of a line by comparing the rise to the run. • The rise is the change in the “y” values while the run is the change in the “x” values. • Slope is often called the rate of change. • We represent slope with the letter m.

Positive Slope Negative Slope Zero Slope Undefined

SLOPE FORMULA

EXAMPLES • Find the slope of the line that is determined by the points (-2, 4) and (4, 2). • Find the slope of the line that goes through the points (3, -3) and (2, -3).

EXAMPLES •

Graph the line that has a slope of -3 and goes through the point (1, 3).

WARM-UP • Find k such that (k, 5) is a solution of 3 x + 2 y = 22 • Find the slope of the line that goes through the points (2, -4) and (-3, -3)

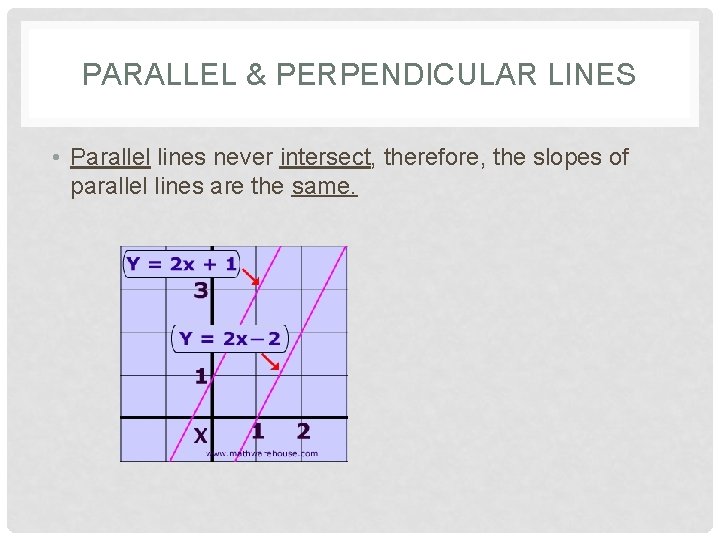
PARALLEL & PERPENDICULAR LINES • Parallel lines never intersect, therefore, the slopes of parallel lines are the same.

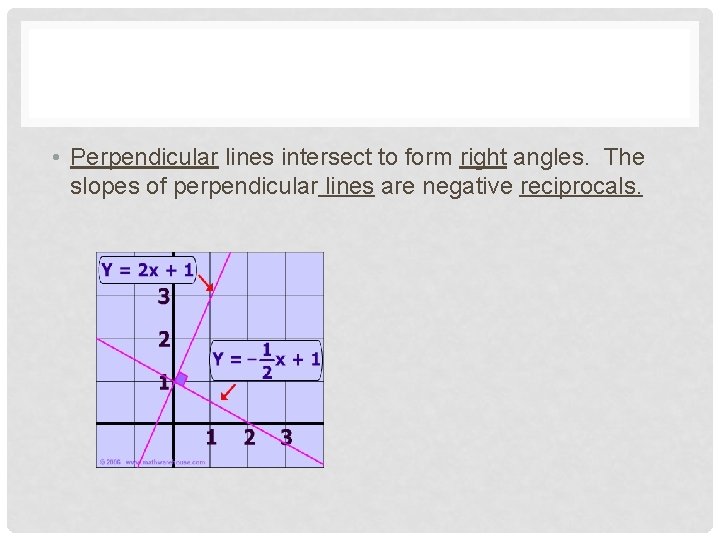
• Perpendicular lines intersect to form right angles. The slopes of perpendicular lines are negative reciprocals.

• When you multiply negative reciprocals, the product is -1. • When writing a negative reciprocal just think “flip and change the sign”.

GUIDED PRACTICE •

WARM - UP •



GRAPHING LINEAR EQUATIONS USING INTERCEPTS • The x intercept is the point at which a function crosses the x-axis. • The y intercept is the point at which a function crosses the y-axis. • If we know these two points, we can graph a line.

KEY POINTS • • Y-intercept: x value is 0; (0, y) X-intercept: y value is 0; (x, 0) To find the x-intercept, substitute 0 in for y and evaluate To find the y-intercept, substitute 0 in for x and evaluate

EXAMPLES

WARM-UP • If line A has a slope of 2 and line B is parallel to it, what is the slope of line B? • What are the x and y intercepts of the line with the equation y = 4 x – 2? • What does the graph of y = - 5 look like?

SLOPE INTERCEPT FORM •

EXAMPLES

WRITING EQUATIONS IN SLOPE INTERCEPT FORM • Given the slope and a point, we can write an equation in slope intercept form and then graph the line. • Method 1: • Substitute the x and y coordinate into y = mx + b • Evaluate to solve for “b” • “Put it all together” in slope intercept form

EXAMPLE 1 • Slope = ½ and goes through the point (2, -3)

EXAMPLE 2 • Write the equation of the line with slope of 2 that goes through the point (4, 6)

EXAMPLE 3 • Write the equation of the line that is parallel to y = 3 x-1 and goes through the point (0, 4)

EXAMPLE 4 • Write the equation of the line that is perpendicular to 7 x – 2 y = 3 and goes through the point (4, -1)

POINT SLOPE FORM •

EXAMPLE 5 • Write the equation of the line that has a slope of 4 and goes through the point (3, 5) then graph the line.

• If we are given two points, we can still write the equation: 1. Find the slope using the points given 2. Substitute the coordinates and slope 3. Evaluate 4. Equation should now be in slope intercept form

EXAMPLE 6 • Write the equation of the line that goes through the points (-3, -4) and (-2, -8).

EXAMPLE 7 • Write the equation of the line that goes through the points (2, 0) and (0, -1).
 Formalizing relations and functions
Formalizing relations and functions Formalizing relations and functions
Formalizing relations and functions Unit 5 polynomial functions homework 7
Unit 5 polynomial functions homework 7 Employee relations in public relations
Employee relations in public relations Graphing sine and cosine quiz
Graphing sine and cosine quiz Sinusoids lesson 4-4 answer key
Sinusoids lesson 4-4 answer key Graphing cube root functions
Graphing cube root functions Xnnn
Xnnn Sine function graph
Sine function graph Graphing linear and exponential functions
Graphing linear and exponential functions Solving graphing and analyzing quadratic functions
Solving graphing and analyzing quadratic functions Function rules examples
Function rules examples 1-2 analyzing graphs of functions and relations answers
1-2 analyzing graphs of functions and relations answers Domain and range of tan function
Domain and range of tan function 2-2 practice linearity and symmetry answers
2-2 practice linearity and symmetry answers Inverse of a relation
Inverse of a relation 6-7 inverse relations and functions
6-7 inverse relations and functions Lesson 1-4 inverses of functions
Lesson 1-4 inverses of functions 4-2 inverses of relations and functions
4-2 inverses of relations and functions 1-2 analyzing graphs of functions and relations
1-2 analyzing graphs of functions and relations 4-2 practice b inverses of relations and functions
4-2 practice b inverses of relations and functions Relations and functions equations
Relations and functions equations Analyzing graphs of functions
Analyzing graphs of functions Implicit function grapher
Implicit function grapher Function vs relation
Function vs relation 6-7 inverse relations and functions
6-7 inverse relations and functions Inverse relations and functions
Inverse relations and functions Relation and function
Relation and function Characteristics of relations and functions
Characteristics of relations and functions Topic 1 relations and functions
Topic 1 relations and functions Linear relations and functions
Linear relations and functions Inverse functions and relations
Inverse functions and relations All real numbers on graph
All real numbers on graph 12-7 graphing trigonometric functions answers
12-7 graphing trigonometric functions answers Lesson 8-1 transformations of functions
Lesson 8-1 transformations of functions Leading coefficient of a polynomial
Leading coefficient of a polynomial 4-5 graphing other trigonometric functions
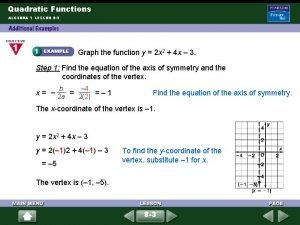
4-5 graphing other trigonometric functions Graphing quadratic functions standard form
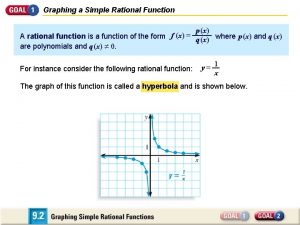
Graphing quadratic functions standard form Graphing rational numbers
Graphing rational numbers Rigid transformation
Rigid transformation 9-1 practice graphing quadratic functions
9-1 practice graphing quadratic functions 9-3 solving quadratic equations by graphing
9-3 solving quadratic equations by graphing Notes for algebra 1
Notes for algebra 1 5-8 practice graphing absolute value functions
5-8 practice graphing absolute value functions Piecewise function word problems
Piecewise function word problems Polynomial function examples
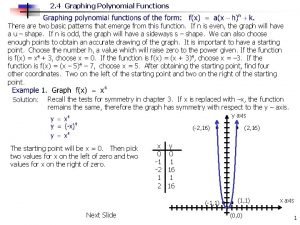
Polynomial function examples 4-1 graphing quadratic functions
4-1 graphing quadratic functions Graphing other trig functions
Graphing other trig functions Graphing absolute value functions calculator
Graphing absolute value functions calculator Graphing exponential functions calculator
Graphing exponential functions calculator Algebra 2b unit 3 exam
Algebra 2b unit 3 exam