6 SOPHISTICATED GRAPHING In graphing functions there is



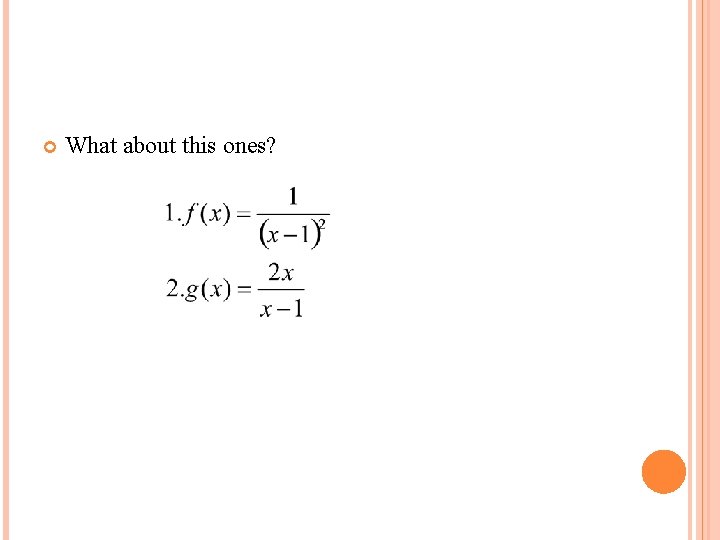






- Slides: 18

6. SOPHISTICATED GRAPHING In graphing functions, there is following procedure will be helpful in most cases : 1. Check Df 2. Test for symmetry (odd or even function) 3. First derivative critical points inc or dec? 4. Local max-min 5. Second derivative concave up/downward, inflection points 6. Asymtot 7. Plot a few points 8. Sketch the graph

ASYMTOT A line is vertical asymtot from a function one of the statements bellow is correct; is

HORIZONTAL ASYMTOT A line is horizontal asymtot from a function y=f(x) if :

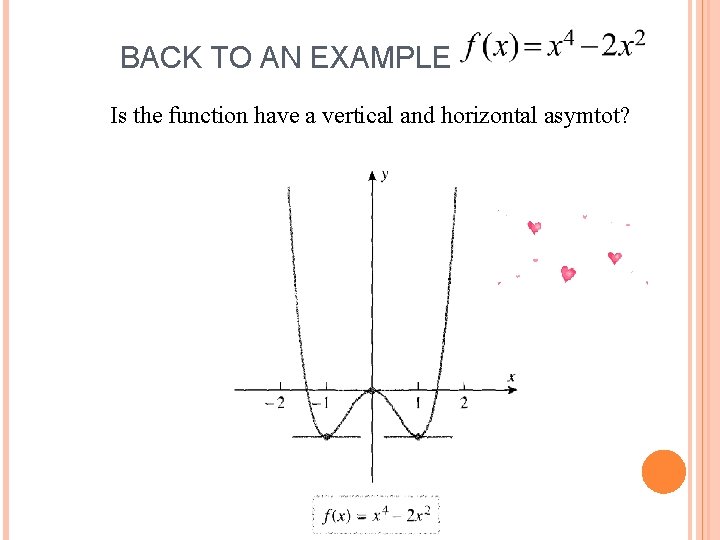
BACK TO AN EXAMPLE Is the function have a vertical and horizontal asymtot?
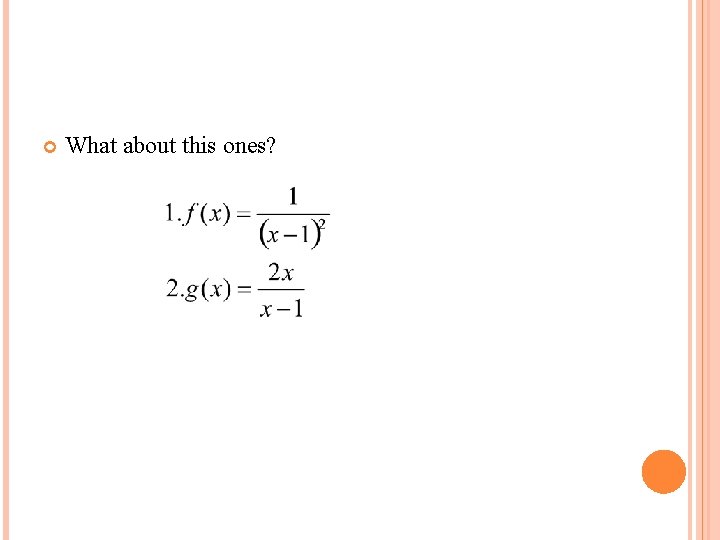
What about this ones?

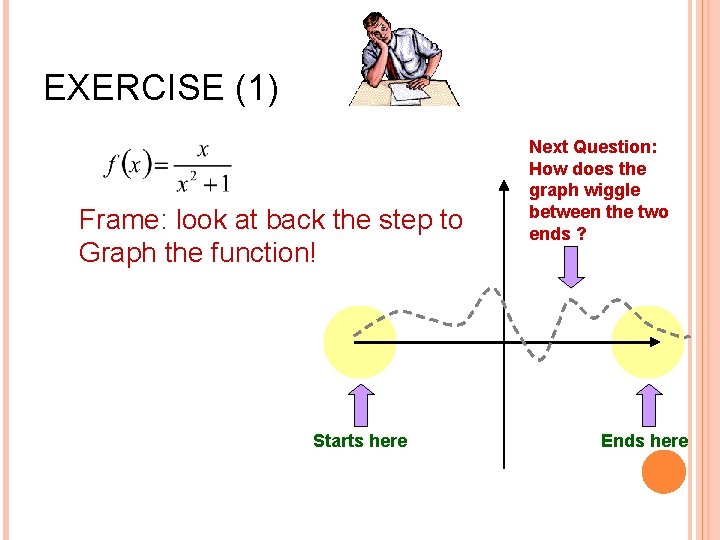
EXERCISE (1) Frame: look at back the step to Graph the function! Starts here Next Question: How does the graph wiggle between the two ends ? Ends here

Derivative: – + – 2 nd derivative: – + 7

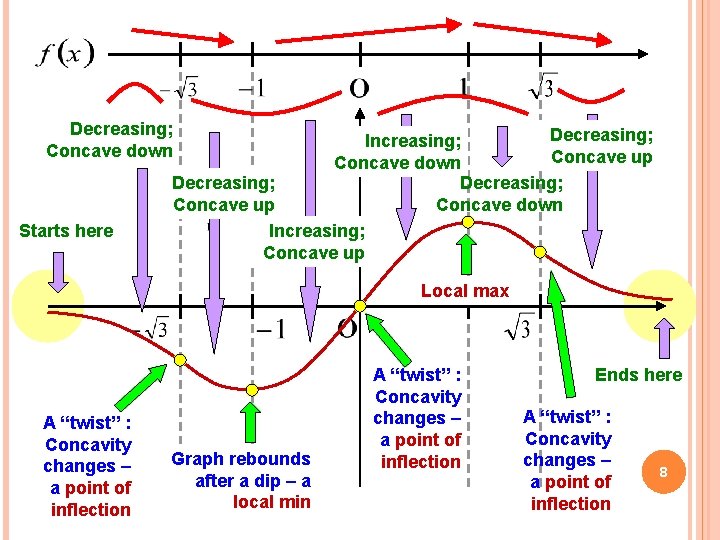
Decreasing; Concave down Starts here Decreasing; Increasing; Concave up Concave down Decreasing; Concave up Concave down Increasing; Concave up Local max A “twist” : Concavity changes – a point of inflection Graph rebounds after a dip – a local min A “twist” : Concavity changes – a point of inflection Ends here A “twist” : Concavity changes – a point of inflection 8

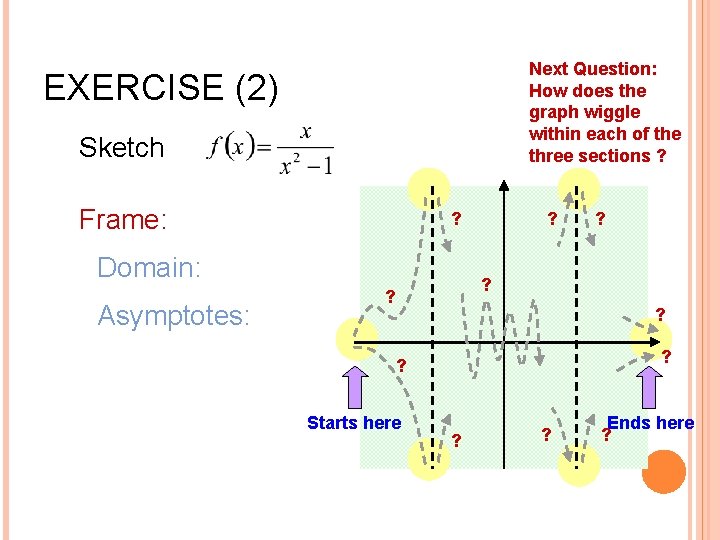
Next Question: How does the graph wiggle within each of the three sections ? EXERCISE (2) Sketch Frame: ? Domain: Asymptotes: ? ? Starts here ? ? ? Ends here ? 9

Wiggle: Derivative: 2 nd derivative: 10

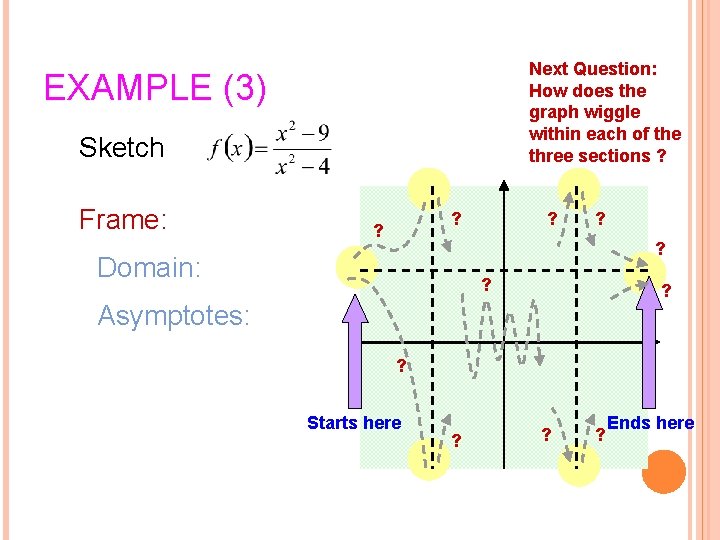
Next Question: How does the graph wiggle within each of the three sections ? EXAMPLE (3) Sketch Frame: ? ? ? Domain: ? ? Asymptotes: ? Starts here ? ? ? Ends here 11

Wiggle: Derivative: 2 nd derivative: 12

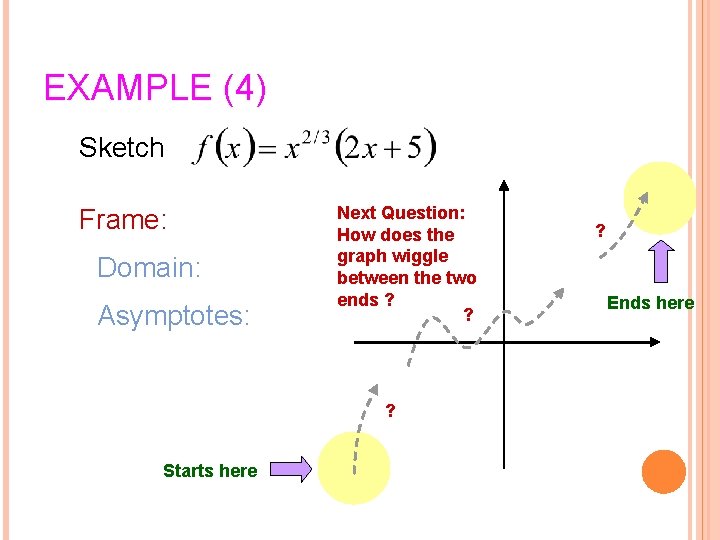
EXAMPLE (4) Sketch Frame: Domain: Asymptotes: Next Question: How does the graph wiggle between the two ends ? ? ? Ends here ? Starts here 13

Wiggle: Derivative: 2 nd derivative: 14

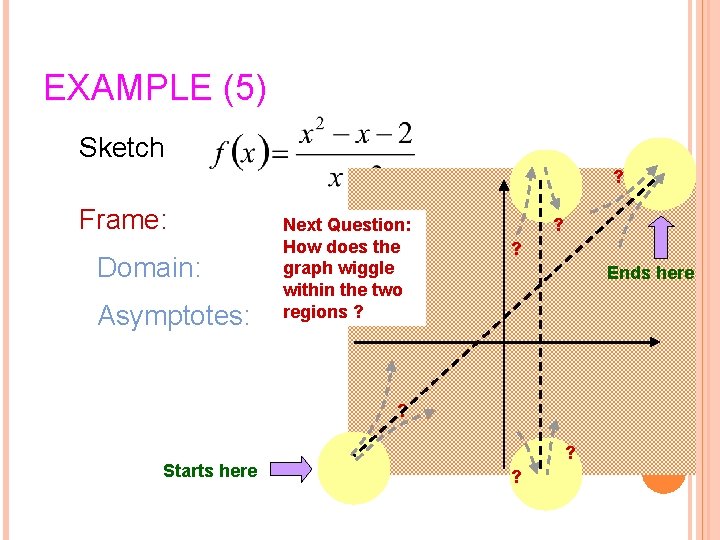
EXAMPLE (5) Sketch ? Frame: Domain: Asymptotes: Next Question: How does the graph wiggle within the two regions ? ? ? Ends here ? Starts here ? ? 15

Wiggle: Derivative: 2 nd derivative: 16

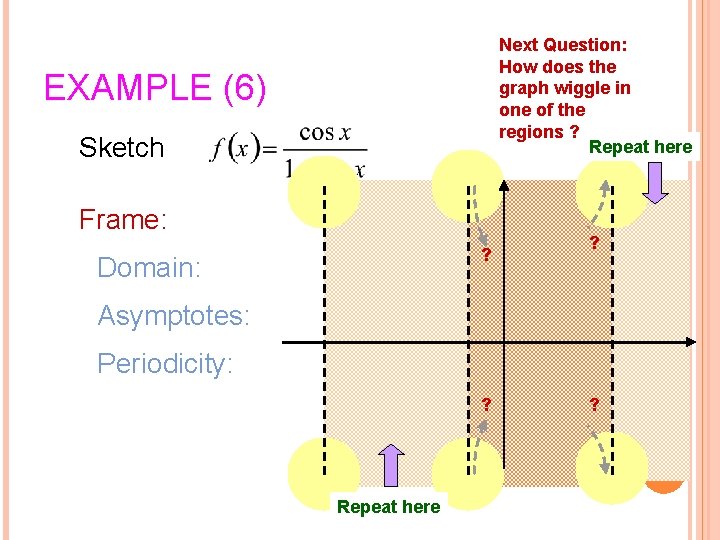
Next Question: How does the graph wiggle in one of the regions ? Repeat here EXAMPLE (6) Sketch Frame: ? Domain: ? Asymptotes: Periodicity: ? Repeat here ? 17

Wiggle: Derivative: 2 nd derivative: 18