Graphing Quadratic Functions Chapter 8 Graphing fx ax
















































- Slides: 53

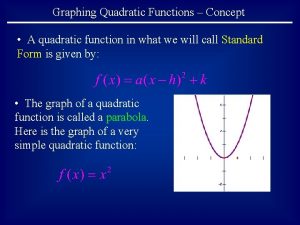
Graphing Quadratic Functions Chapter 8

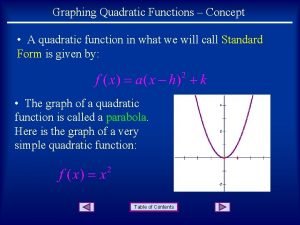
Graphing f(x) = ax 2 + bx + c I can graph quadratic functions of the form f(x) = ax 2 + bx + c.

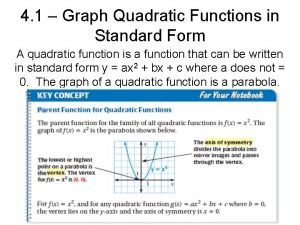
Graphing f(x) = ax 2 + bx + c Vocabulary (page 247 in Student Journal) quadratic function: a nonlinear function of the second degree parabola: the u-shaped curve of the graph of a quadratic function

Graphing f(x) = ax 2 + bx + c vertex: the lowest, or highest, point on a parabola, which is on the axis of symmetry: the line that divides a parabola into 2 matching halves

Graphing f(x) = ax 2 + bx + c Vocabulary (page 252 in Student Journal) zero of a function: the value of x that makes y = 0 in a quadratic function, which is the place(s) where the parabola intersects the x-axis on the graph

Graphing f(x) = ax 2 + bx + c Vocabulary (page 257 in Student Journal) maximum value: the y-coordinate of the vertex when the parabola opens down (a < 0) minimum value: the y-coordinate of the vertex when the parabola opens up (a > 0)

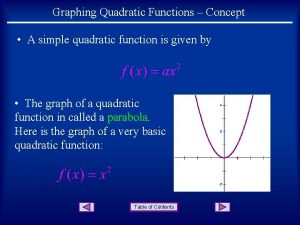
Graphing f(x) = ax 2 + bx + c Core Concepts (pages 247 and 248 in Student Journal) Graphing f(x) = ax 2 -when a > 1 the graph of f(x) = x 2 is a vertical stretch -when 0 < a < 1 the graph of f(x) = x 2 is a vertical shrink

Graphing f(x) = ax 2 + bx + c Graphing f(x) = ax 2 (continued) -when a < -1 the graph of f(x) = x 2 is a vertical stretch and is reflected in the x-axis -when -1 < a < 0 the graph of f(x) = x 2 is a vertical shrink and is reflected in the xaxis

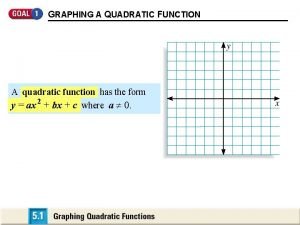
Graphing f(x) = ax 2 + bx + c Core Concepts (page 257 in Student Journal) Graphing f(x) = ax 2 + bx + c -when a > 0, the graph opens up -when a < 0, the graph opens down -the y-intercept is c -the x-coordinate of the vertex is –b/2 a

Graphing f(x) = ax 2 + bx + c

Graphing f(x) = ax 2 + bx + c Solution #1) x = 5, (5, -23)

Graphing f(x) = ax 2 + bx + c

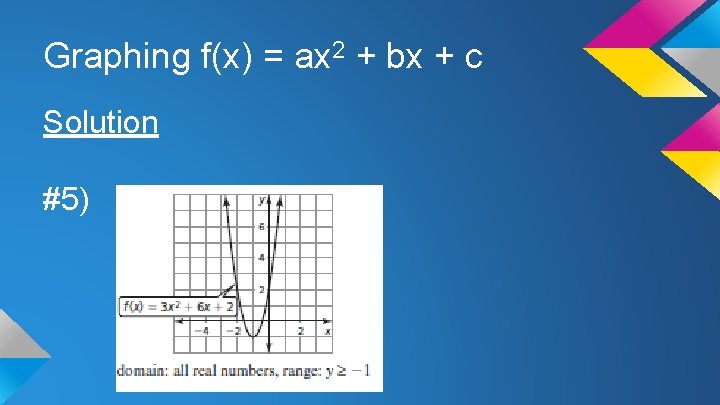
Graphing f(x) = ax 2 + bx + c Solution #5)

Graphing f(x) = ax 2 + bx + c

Graphing f(x) = ax 2 + bx + c Solution #8) maximum, y = 14. 5

Graphing f(x) = ax 2 + bx + c

Graphing f(x) = ax 2 + bx + c Solutions #14 a) 7. 8125 seconds #14 b) 976. 5625 feet

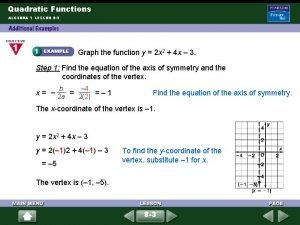
Graphing f(x) = ax 2 Additional Example (space on pages 257 and 258 in Student Journal) a) Identify the vertex, axis of symmetry, domain and range based on the graph.

Graphing f(x) = ax 2 Solution a) vertex at (2, -4), axis of symmetry is x = 2, domain is all real numbers, range is y greater than or equal to -4

Graphing f(x) = a(x – h)2 + k I can graph quadratic functions in the form f(x) = a(x – h)2 + k.

Graphing f(x) = a(x – h)2 + k Vocabulary (page 262 in Student Journal) vertex form (of a quadratic function): a quadratic function in the form f(x) = a(x – h)2 + k

Graphing f(x) = a(x – h)2 + k Core Concepts (pages 262 and 263 in Student Journal) Graphing f(x) = a(x – h)2 + k -a is the vertical stretch/shrink factor -h is the horizontal translation -k is the vertical translation -(h, k) are the coordinates of the vertex

Graphing f(x) = a(x – h)2 + k

Graphing f(x) = a(x – h)2 + k Solutions #5) (2, 0), x = 2 #8) (-1, -5), x = -1

Graphing f(x) = a(x – h)2 + k

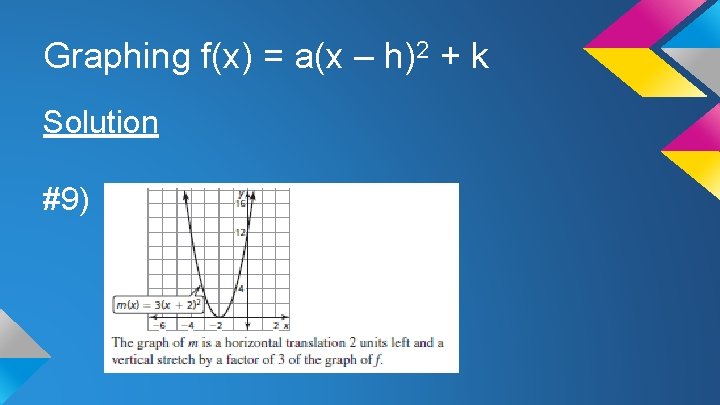
Graphing f(x) = a(x – h)2 + k Solution #9)

Graphing f(x) = a(x – h)2 + k Additional Example (space on pages 262 and 263 in Student Journal) a) Write and graph a quadratic function that models the path of a stream of water from a fountain that has a maximum height of 4 feet at a time of 3 seconds and lands after 6 seconds.

Graphing f(x) = a(x – h)2 + k Solution a) y = -4/9(x – 3)2 + 4

Using Intercept Form I can graph quadratic functions of the form f(x) = a(x – p)(x – q).

Using Intercept Form Vocabulary (page 267 in Student Journal) intercept form: a quadratic function written in factored, which is f(x) = a(x – p)(x – q)

Using Intercept Form Core Concepts (page 267 in Student Journal) Graphing f(x) = a(x – p)(x – q) -x-intercepts are p and q -axis of symmetry is x = (p + q)/2 -a is the vertical stretch/shrink factor

Using Intercept Form

Using Intercept Form Solution #1) x-intercepts: -2, 4 axis of symmetry: x = 1

Using Intercept Form

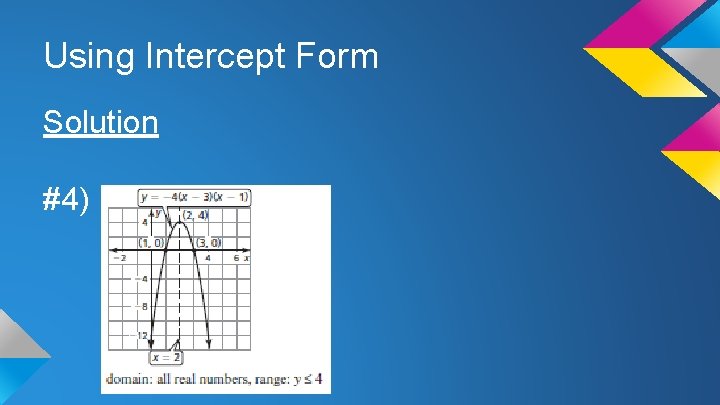
Using Intercept Form Solution #4)

Using Intercept Form

Using Intercept Form Solution #7) 1, -1

Using Intercept Form

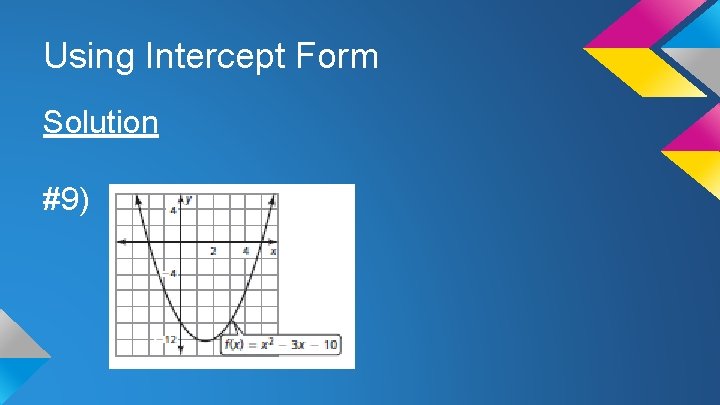
Using Intercept Form Solution #9)

Using Intercept Form Additional Examples (space on page 267 in Student Journal) Write a quadratic function in standard form that satisfies the given conditions. a) zeros at -1 and 5 b) vertex at (-3, -2)

Using Intercept Form Possible Solutions a) y = x 2 – 4 x – 5 b) y = x 2 + 6 x + 7

Comparing Linear, Exponential, and Quadratic Functions I can choose and write functions to model data.

Comparing Linear, Exponential, and Quadratic Functions Vocabulary (page 272 in Student Journal) average rate of change: the slope of the line connecting 2 points on a graph

Comparing Linear, Exponential, and Quadratic Functions Core Concepts (pages 272 and 273 in Student Journal) Linear, Exponential, and Quadratic Functions linear: y = mx + b exponential: y = abx quadratic: y = ax 2 + bx + c

Comparing Linear, Exponential, and Quadratic Functions Differences and Ratios of Functions linear: first differences of y-values are constant exponential: consecutive y-values have common ratio quadratic: second differences of yvalues are constant

Comparing Linear, Exponential, and Quadratic Functions Examples (pages 273 and 274 in Student Journal) Determine if the ordered pairs represent a linear, exponential or quadratic function. #1) (-3, 2), (-2, 4), (-4, 4), (-1, 8), (-5, 8) #2) (-3, 1), (-2, 2), (-1, 4), (0, 8), (2, 14)

Comparing Linear, Exponential, and Quadratic Functions Solutions #1) quadratic #2) exponential

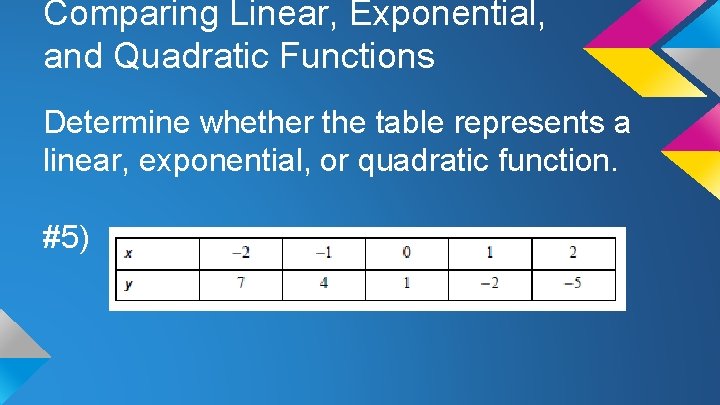
Comparing Linear, Exponential, and Quadratic Functions Determine whether the table represents a linear, exponential, or quadratic function. #5)

Comparing Linear, Exponential, and Quadratic Functions Solutions #5) linear

Comparing Linear, Exponential, and Quadratic Functions Tell whether the data represents a linear, exponential, or quadratic function. Then write the function. #8) (-2, -9), (-1, 0), (0, 3), (1, 0), (2, -9)

Comparing Linear, Exponential, and Quadratic Functions

Comparing Linear, Exponential, and Quadratic Functions Additional Example (space on pages 272 and 273 in Student Journal) a) Two news website open their memberships to the public. Which site would you predict will have more members after 50 days? Why?

Comparing Linear, Exponential, and Quadratic Functions Solution a) Website B, because the relationship appears to be exponential, which means the average rate of change will eventually exceed the average rate of change of website A, which is linear.
 Suppose a particular star is projected from a firework
Suppose a particular star is projected from a firework Graphing quadratic functions in standard form
Graphing quadratic functions in standard form 9-1 practice graphing quadratic functions
9-1 practice graphing quadratic functions Vertex x coordinate
Vertex x coordinate Algebra picture
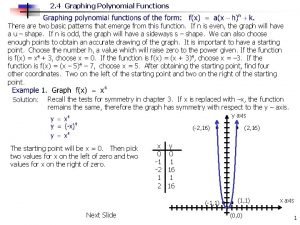
Algebra picture 4-1 graphing quadratic functions
4-1 graphing quadratic functions 9-3 graphing quadratic functions
9-3 graphing quadratic functions 9-1 graphing quadratic functions
9-1 graphing quadratic functions Vertex of quadratic function
Vertex of quadratic function Y=a(x-p)(x-q) how to find a
Y=a(x-p)(x-q) how to find a Solving graphing and analyzing quadratic functions
Solving graphing and analyzing quadratic functions 4-1 graphing quadratic functions
4-1 graphing quadratic functions Standard form from graph
Standard form from graph 9-1 practice graphing quadratic functions
9-1 practice graphing quadratic functions Quadratic formula vocabulary
Quadratic formula vocabulary Y intercept in quadratic function
Y intercept in quadratic function Graphing a quadratic function
Graphing a quadratic function Chapter 3 graphing linear functions answer key
Chapter 3 graphing linear functions answer key Chapter 9 quadratic equations and functions
Chapter 9 quadratic equations and functions Chapter 8 quadratic functions and equations answer key
Chapter 8 quadratic functions and equations answer key Lesson 8 quadratic functions page 339
Lesson 8 quadratic functions page 339 Exploring quadratic functions
Exploring quadratic functions Chapter 3 linear and quadratic functions
Chapter 3 linear and quadratic functions Chapter 1 quadratic functions and factoring
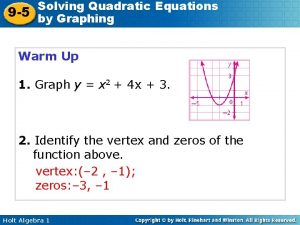
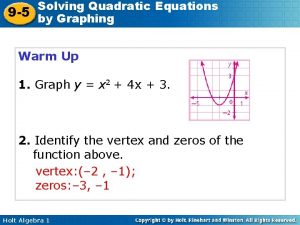
Chapter 1 quadratic functions and factoring 9-5 solving quadratic equations by graphing
9-5 solving quadratic equations by graphing 9-5 solving quadratic equations by graphing
9-5 solving quadratic equations by graphing Objectives of quadratic equation
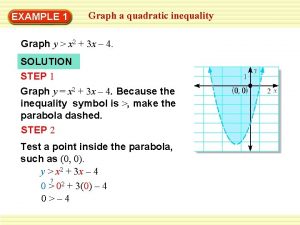
Objectives of quadratic equation Graphing quadratic inequalities
Graphing quadratic inequalities Graphing linear-quadratic systems
Graphing linear-quadratic systems How do you know where to shade in a quadratic inequality
How do you know where to shade in a quadratic inequality Quadratic inequality examples
Quadratic inequality examples 4-2 solving quadratic equations by graphing
4-2 solving quadratic equations by graphing Quadratic inequalities in one variable
Quadratic inequalities in one variable Graphing systems of quadratic inequalities
Graphing systems of quadratic inequalities How to find roots of equation
How to find roots of equation Ax^2 +bx +c
Ax^2 +bx +c 8-1 identifying quadratic functions
8-1 identifying quadratic functions How to graph quadratic inequalities
How to graph quadratic inequalities 5-2 solving quadratic equations by graphing
5-2 solving quadratic equations by graphing 9-5 solving quadratic equations by graphing
9-5 solving quadratic equations by graphing Solving linear-quadratic systems by elimination
Solving linear-quadratic systems by elimination Quadratic formula examples
Quadratic formula examples All real numbers graph
All real numbers graph Unit 5: polynomial functions
Unit 5: polynomial functions 12-7 graphing trigonometric functions answers
12-7 graphing trigonometric functions answers Graphing sine and cosine quiz
Graphing sine and cosine quiz What is the leading coefficient of a polynomial
What is the leading coefficient of a polynomial 4-5 practice graphing other trigonometric functions
4-5 practice graphing other trigonometric functions Sinusoids lesson 4-4 answer key
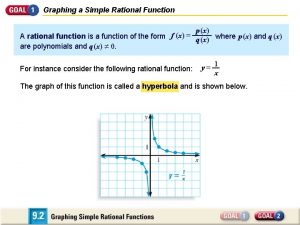
Sinusoids lesson 4-4 answer key Rational function graph in real life
Rational function graph in real life What is rigid and non rigid
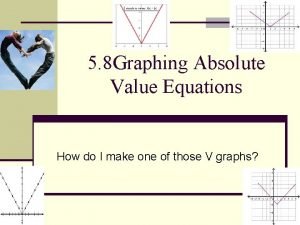
What is rigid and non rigid 5-8 practice graphing absolute value functions
5-8 practice graphing absolute value functions Your cell phone plan costs $75
Your cell phone plan costs $75 (-2 4) graph
(-2 4) graph