Chapter 2 Linear Relations Functions 2 1 relations

Chapter 2 Linear Relations & Functions

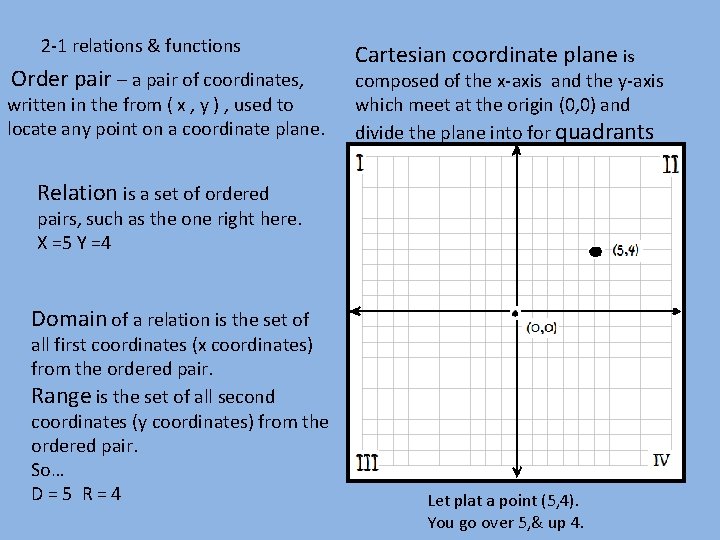
2 -1 relations & functions Order pair – a pair of coordinates, written in the from ( x , y ) , used to locate any point on a coordinate plane. Cartesian coordinate plane is composed of the x-axis and the y-axis which meet at the origin (0, 0) and divide the plane into for quadrants Relation is a set of ordered pairs, such as the one right here. X =5 Y =4 Domain of a relation is the set of all first coordinates (x coordinates) from the ordered pair. Range is the set of all second coordinates (y coordinates) from the ordered pair. So… D=5 R=4 Let plat a point (5, 4). You go over 5, & up 4.

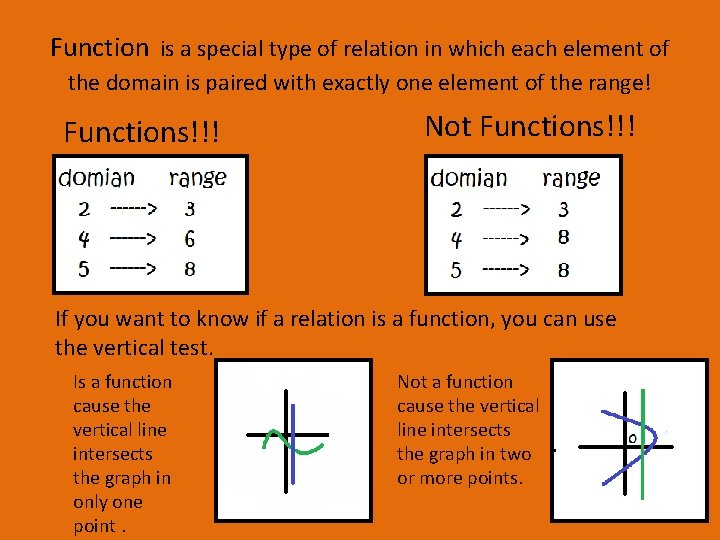
Function is a special type of relation in which each element of the domain is paired with exactly one element of the range! Functions!!! Not Functions!!! If you want to know if a relation is a function, you can use the vertical test. Is a function cause the vertical line intersects the graph in only one point. Not a function cause the vertical line intersects the graph in two or more points.

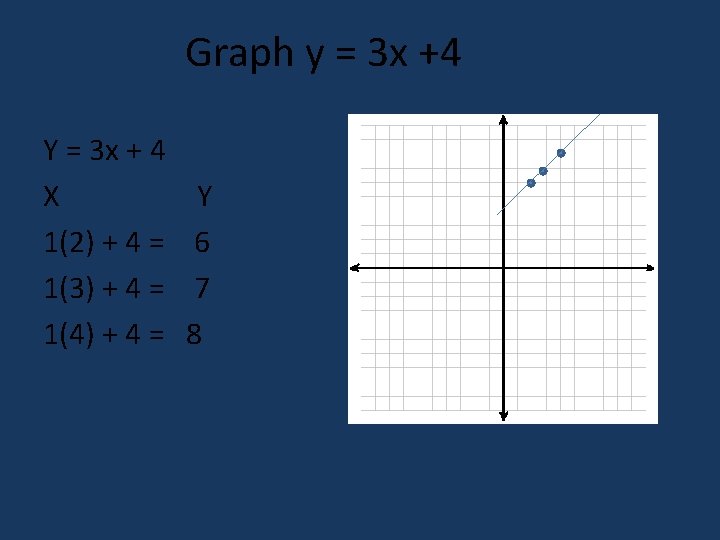
Graph y = 3 x +4 Y = 3 x + 4 X 1(2) + 4 = 1(3) + 4 = 1(4) + 4 = Y 6 7 8

Function notation is an equation of y in terms if x can be rewritten so that y = f(x). For example: y = 1 x + 7 can be written as f(x) = 1 x + 7 What is f(x) = 1 x + 7 if x = 2. f(2) = 1(2) + 7 f(2) = 2 + 7 f(2) = 9

2 -2 linear equations A linear equation could be x + y= 5. • The Graph of a linear equation is always a straight line. • As long as you go by the following conditions its easy to defined a easier equation, • The Variables can have no exponents greater then 1. • The Variables cannot be multiplied together. • The Variables cannot be in the denominator • The variables cannot be under a radical.

A Linear Function is a function whose ordered Paris satisfies a linear equation. A linear function is a function whose ordered pairs satisfies a linear equation. Any linear functions can be written y = mx + b, where m and b are real number. f(x)=10 -5 x : This is a linear function because it can be written as f(x)=-5 x+10. m=5, b=10 These are not a liner equations, G(x)=x 4 -5 : This is not a linear function because x has an exponent other then 1. H(x , y)=2 xy : this is not a liner function because the two variables are multiplied together

Standard form of al linear Equation, • Ax + By=C : • A cannot be negative • B & C cannot both be 0 y=2 x+2 -2 -2 -2 +y = 2 multiply each side by -1 so that A = or greater then 0. 2 – y = -2 A = 2 B = -1 C =-2

If You know where the line crosses the x and y axis, it would be much easier to graph the line. You can use the slandered form to find the intercepts. The x-intercept is the value of x when y = 0, and the y=intercept is the value of y when x = 0. So let find the x intercept. 3 x-4 y-12=0 +12 3 x-4 y=12 3 x-4(0)=12 3 x-0=12 3 x/3=12/3 X=4 So Your x intercept is x = 4 3 x - 4 y - 12 = 0 +12 3 x - 4 y = 12 3( 0) – 4 y = 12 0 – 4 y = 12 4 y/4 = 12/4 y=3 So your y intercept is y = 3

2 -3 slope The slope of a line is the ratio of the change in ycoordinates to the corresponding change in xcoordinates. Slope = change in y-coordinates change in x-coordinates = y 2 – y 1 x 2 – x 1 The slope of a line is the same, no matter what two points on the line are used.

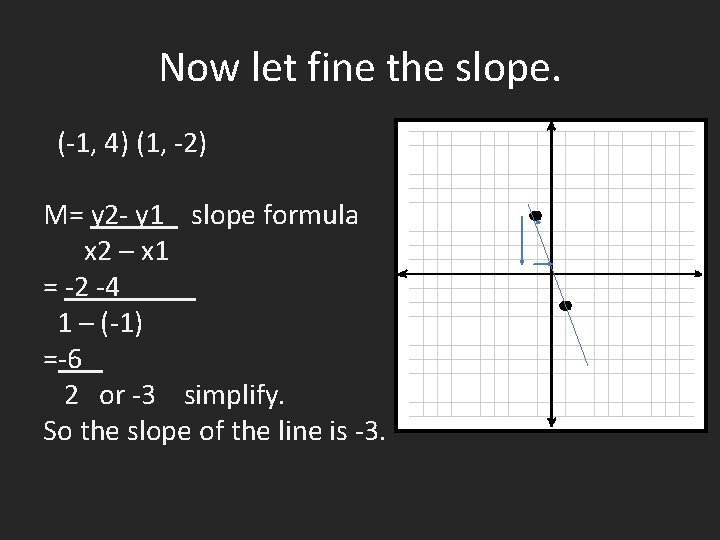
Now let fine the slope. (-1, 4) (1, -2) M= y 2 - y 1 slope formula x 2 – x 1 = -2 -4 1 – (-1) =-6 2 or -3 simplify. So the slope of the line is -3.

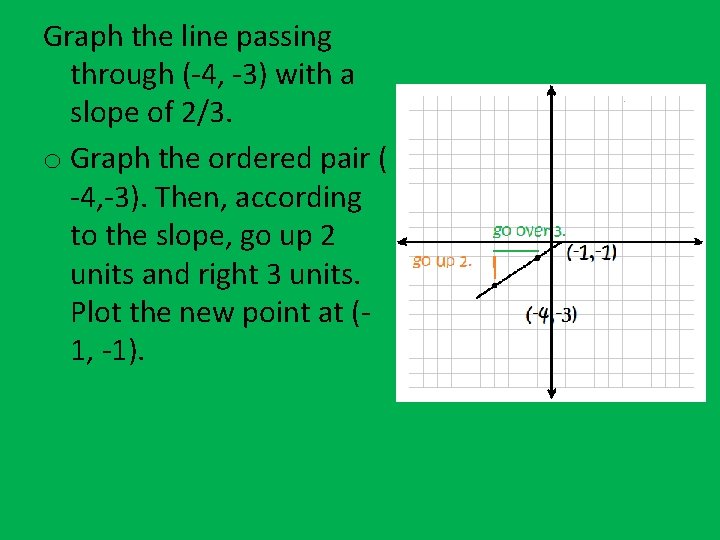
Graph the line passing through (-4, -3) with a slope of 2/3. o Graph the ordered pair ( -4, -3). Then, according to the slope, go up 2 units and right 3 units. Plot the new point at (1, -1).

Write an equation in slop-intercept from for the line that has a slope of – 3/2 and passes through (-4, 1). y = mx + b slope –intercept form. 1 = (-3/2) (-4) + b (x, y) = (-4, 1) , m= -3/2 1=6+b simplify -5 = b subtract 6 from each side. The y-intercept is -5. So, the equation in slopintercept form is y = -3/2 x – 5.

If you want any more look in here hehe I'm just joking…