Geometric Sequences and Series Arithmetic Sequences Geometric Sequences













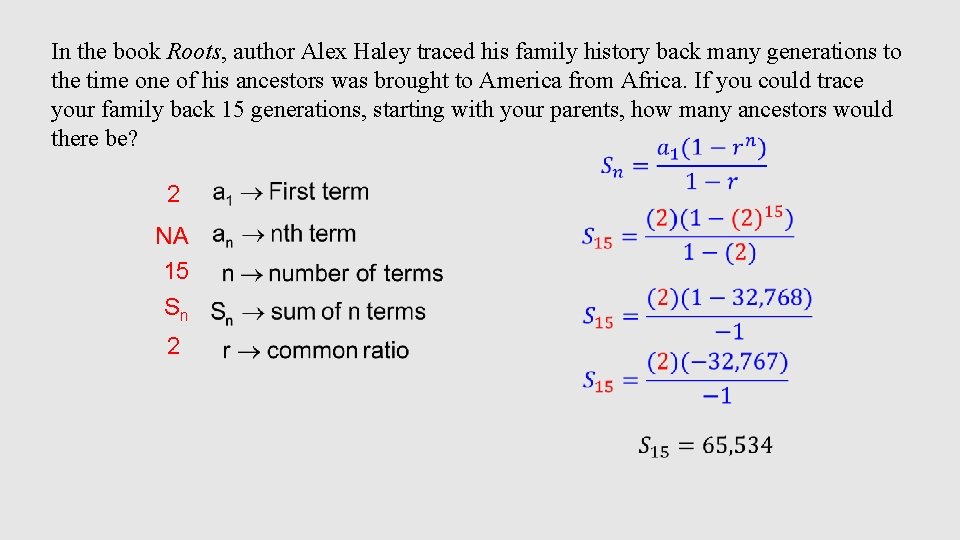














- Slides: 30

Geometric Sequences and Series

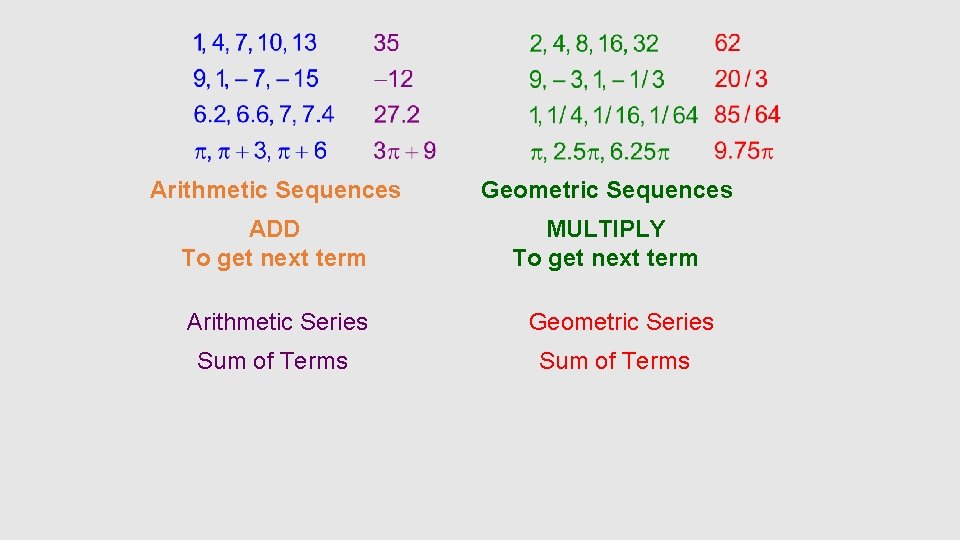
Arithmetic Sequences Geometric Sequences ADD To get next term MULTIPLY To get next term Arithmetic Series Geometric Series Sum of Terms

• Geometric Sequence: sequence whose consecutive terms have a common ratio. • • Example: 3, 6, 12, 24, 48, . . . The terms have a common ratio of 2. The common ratio is the number r. To find the common ratio you use an+1 ÷ an

Vocabulary of Sequences (Universal)

Find the next two terms of 2, 6, 18, ___ 6 – 2 vs. 18 – 6… not arithmetic 2, 6, 18, 54, 162 Find the next two terms of 80, 40, 20, ___ 40 – 80 vs. 20 – 40… not arithmetic 80, 40, 20, 10, 5

Find the next two terms of -15, 30, -60, ___ 30 – -15 vs. -60 – 30… not arithmetic -15, 30, -60, 120, -240 Find the next three terms of 2, 3, 9/2, ___, ___ 3 – 2 vs. 9/2 – 3… not arithmetic

Find the 8 th term if a 1 = -3 and r = -2. -3 an 8 NA -2

Find the 10 th term if a 4 = 108 and r = 3. 4 ? ? an 10 NA 3

Write an equation for the nth term of the geometric sequence 3, 12, 48, 192, … 3 4

Geometric Mean: The terms between any two nonconsecutive terms of a geometric sequence. Ex. 2, 6, 18, 54, 162 6, 18, 54 are the Geometric Mean between 2 and 162

Find two geometric means between – 2 and 54 -2, ____, 54 -2 54 4 NA r The two geometric means are 6 and -18, since – 2, 6, -18, 54 forms a geometric sequence

Geometric Series: An indicated sum of terms in a geometric sequence. Example: Geometric Sequence 3, 6, 12, 24, 48 VS Geometric Series 3 + 6 + 12 + 24 + 48

Recall Vocabulary of Sequences (Universal)

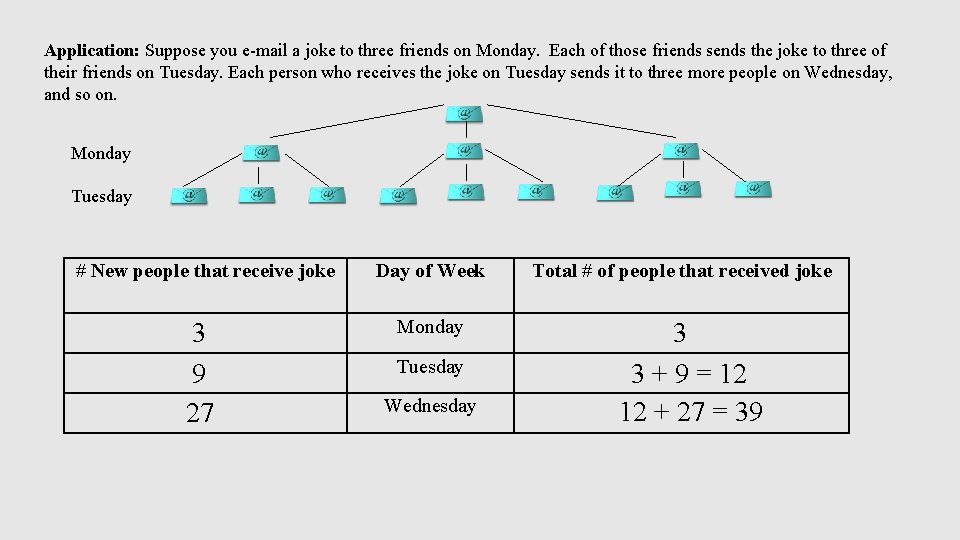
Application: Suppose you e-mail a joke to three friends on Monday. Each of those friends sends the joke to three of their friends on Tuesday. Each person who receives the joke on Tuesday sends it to three more people on Wednesday, and so on. Monday Tuesday # New people that receive joke Day of Week 3 9 27 Monday Tuesday Wednesday Total # of people that received joke 3 3 + 9 = 12 12 + 27 = 39

Find the sum of the first 10 terms of the geometric series 3 - 6 + 12 – 24+ … 3 10 Sn -2
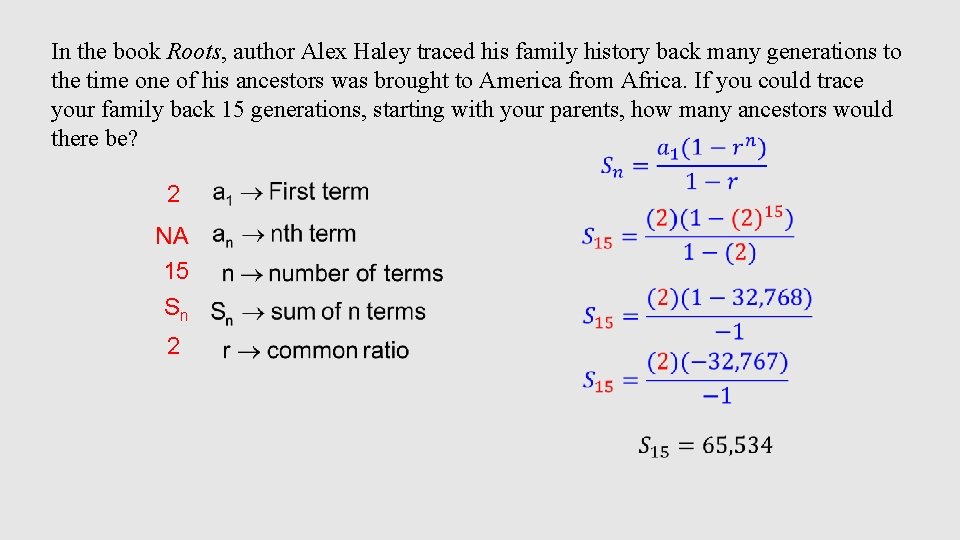
In the book Roots, author Alex Haley traced his family history back many generations to the time one of his ancestors was brought to America from Africa. If you could trace your family back 15 generations, starting with your parents, how many ancestors would there be? 2 15 Sn 2

a 1 NA 8 39, 360 3

15, 625 -5 ? ? Sn

Recall the properties of exponents. When multiplying like bases add exponents

15, 625 -5 ? ? Sn

UPPER LIMIT (NUMBER) SIGMA (SUM OF TERMS) INDEX NTH TERM (SEQUENCE) LOWER LIMIT (NUMBER)

If the sequence is geometric (has a common ratio) you can use the Sn formula 5· 20 = 5 5· 25 = 160 6 Sn 2

Rewrite using sigma notation: 16 + 8 + 4 + 2 + 1 Geometric, r = ½

Infinite Series

1, 4, 7, 10, 13, …. Infinite Arithmetic 3, 7, 11, …, 51 Finite Arithmetic 1, 2, 4, …, 64 Finite Geometric 1, 2, 4, 8, … Infinite Geometric r>1 r < -1 Infinite Geometric -1 < r < 1 No Sum

Find the sum, if possible:

Find the sum, if possible:

Find the sum, if possible:

Find the sum, if possible:

Find the sum, if possible: