Geometric Sequences and Series Geometric Sequences Geometric Series

Geometric Sequences and Series Geometric Sequences Geometric Series Infinite Geometric Series Annuities 7. 3 - 1

Geometric Sequences Suppose you agreed to work for 1¢ the first day, 2¢ the second day, 4¢ the third day, 8¢ the fourth day, and so on, with your wages doubling each day. How much will you earn on day 20, after working 5 days a week for a month? How much will you have earned altogether in 20 days? These questions will be answered in this section. 7. 3 - 2

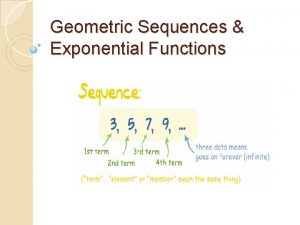
Geometric Sequences A geometric sequence (or geometric progression) is a sequence in which each term after the first is obtained by multiplying the preceding term by a fixed nonzero real number, called the common ratio. The sequence discussed in the last slide, is an example of a geometric sequence in which the first term is 1 and the common ratio is 2. 7. 3 - 3

Geometric Sequences Notice that if we divide any term after the first term by the preceding term, we obtain the common ratio r = 2. 7. 3 - 4

Geometric Sequences If the common ratio of a geometric sequence is r, then by the definition of a geometric sequence, Common ratio r for every positive integer n. Therefore, we find the common ratio by choosing any term except the first and dividing it by the preceding term. 7. 3 - 5

Geometric Sequences In the geometric sequence 2, 8, 32, 128, …, r = 4. Notice that To generalize this, assume that a geometric sequence has first term and common ratio r. The second term is a 2 = a 1 r, the third is a 3 = a 2 r, and so on. Following this pattern, the nth term is an = a 1 r n – 1. Again, this result can be proved by mathematical induction. 7. 3 - 6

nth Term of a Geometric Sequence In a geometric sequence with first term a 1 and common ratio r, the nth term, an, is given by 7. 3 - 7

Example 1 FINDING THE nth TERM OF A GEOMETRIC SEQUENCE Use the formula for the nth term of a geometric sequence to answer the first question posed at the beginning of this section. How much will be earned on day 20 if daily wages follow the sequence 1, 2, 4, 8, 16, …cents? Solution 7. 3 - 8

Example 2 FINDING TERMS OF A GEOMETRIC SEQUENCE Find a 5 and an for the geometric sequence 4, 12, 36, 108, …. Solution The first term, a 1, is 4. Find r by choosing any term after the first and dividing it by the preceding term. For example, By the formula, 7. 3 - 9

Example 3 FINDING TERMS OF A GEOMETRIC SEQUENCE Find r and a 1 for the geometric sequence with third term 20 and sixth term 160. Solution Use the formula for the nth term of a geometric sequence. For n = 3, a 3 = a 1 r 2 = 20. For n = 6, a 6 = a 1 r 5 = 160. 7. 3 - 10

Example 3 FINDING TERMS OF A GEOMETRIC SEQUENCE Find r and a 1 for the geometric sequence with third term 20 and sixth term 160. Solution Since Substitute this value for a 1 in the second equation. Quotient rule for exponents Divide by 20. Substitute. Take cube roots. 7. 3 - 11

Example 3 FINDING TERMS OF A GEOMETRIC SEQUENCE Find r and a 1 for the geometric sequence with third term 20 and sixth term 160. Solution Since Substitute. Divide by 4. 7. 3 - 12

Example 4 MODELING A POPULATION OF FRUIT FLIES A population of fruit flies is growing in such a way that each generation is 1. 5 times as large as the last generation. Suppose there were 100 insects in the first generation. How many would there be in the fourth generation? 7. 3 - 13

Example 4 MODELING A POPULATION OF FRUIT FLIES Solution Write the population of each generation as a geometric sequence with a 1 as the first-generation population, a 2, the second-generation population, and so on. Then the fourth-generation population is a 4. Using the formula for an, with n = 4, r = 1. 5, and a 1 = 100, gives In the fourth generation, the population will number about 338 insects. 7. 3 - 14

Geometric Series A geometric series is the sum of the terms of a geometric sequence. In applications, it may be necessary to find the sum of the terms of such a sequence. For example, a scientist might want to know the total number of insects in four generations of the population discussed in Example 4. 7. 3 - 15

Geometric Series This population would equal or 7. 3 - 16

Geometric Series To find a formula for the sum of the first n terms of a geometric sequence, Sn, first write the sum as or (1) 7. 3 - 17

Geometric Series If r = 1, then Sn = na 1, which is a correct formula for this case. If r ≠ 1, then multiply both sides of equation (1) by r to obtain (2) 7. 3 - 18

Geometric Series If equation (2) is subtracted from equation (1), (1) (2) Subtract. Factor. Divide by 1–r. 7. 3 - 19

Sum of the First n Terms of a Geometric Sequence If a geometric sequence has first term a 1 and common ratio r, then the sum of the first n terms is given by 7. 3 - 20

Geometric Series We can use a geometric series to find the total fruit fly population in Example 4 over the fourgeneration period. With n = 4, a 1 =100, and r = 1. 5, which agrees with our previous result. 7. 3 - 21

Example 5 FINDING THE SUM OF THE FIRST n TERMS At the beginning of this section, we posed the following question: How much will you have earned altogether after 20 days? Answer this question. Solution We must find the total amount earned in 20 days with daily wages of 1, 2, 4, 8, …cents. Since a 1 = 1 and r = 2, or 7. 3 - 22

Example 6 FINDING THE SUM OF THE FIRST n TERMS Find Solution This series is the sum of the first six terms of a geometric sequence having a 1 = 2 ● 31 = 6 and r = 3. Using the formula for Sn, 7. 3 - 23

Infinite Geometric Series We extend our discussion of sums of sequences to include infinite geometric sequences such as with first term 2 and common ratio ½. Using the formula for Sn gives the following sequence of sums. 7. 3 - 24

Infinite Geometric Series The formula for Sn can also be written as As this formula suggests, these sums seem to be getting closer and closer to the number 4. For no value of n is Sn = 4. However, if n is large enough, then Sn is as close to 4 as desired. 7. 3 - 25

Infinite Geometric Series As mentioned earlier, we say the sequence converges to 4. This is expressed as (Read: “the limit of Sn as n increases without bound is 4. ”) 7. 3 - 26

Infinite Geometric Series Since the number 4 is called the sum of the terms of the infinite geometric sequence and 7. 3 - 27

Example 7 SUMMING THE TERMS OF AN INFINITE GEOMETRIC SERIES Evaluate Solution Use the formula for the sum of the first n terms of a geometric sequence to obtain and, in general, Let a 1 = 1, r = 1/3. 7. 3 - 28

Example 7 SUMMING THE TERMS OF AN INFINITE GEOMETRIC SERIES The table shows the value of (1/3)n for larger and larger values of n. n 1 10 100 200 7. 3 - 29

Example 7 SUMMING THE TERMS OF AN INFINITE GEOMETRIC SERIES As n gets larger and larger, gets closer and closer to 0. That is, making it reasonable that Hence, 7. 3 - 30

Example 7 SUMMING THE TERMS OF AN INFINITE GEOMETRIC SERIES If a geometric series has first term a 1 and common ratio r, then for every positive integer n. If – 1< r < 1, then limrn = 0, and 7. 3 - 31

This quotient, is called the sum of the terms of an infinite geometric sequence. The limit is often expressed as 7. 3 - 32

Sum of The Terms of an Infinite Geometric Sequence The sum of the terms of an infinite geometric sequence with first term a 1 and common ratio r, where – 1 < r < 1, is given by If │r│> 1, then the terms get larger and larger in absolute value, so there is no limit as n →∞. Hence the terms of the sequence will not have a sum. 7. 3 - 33

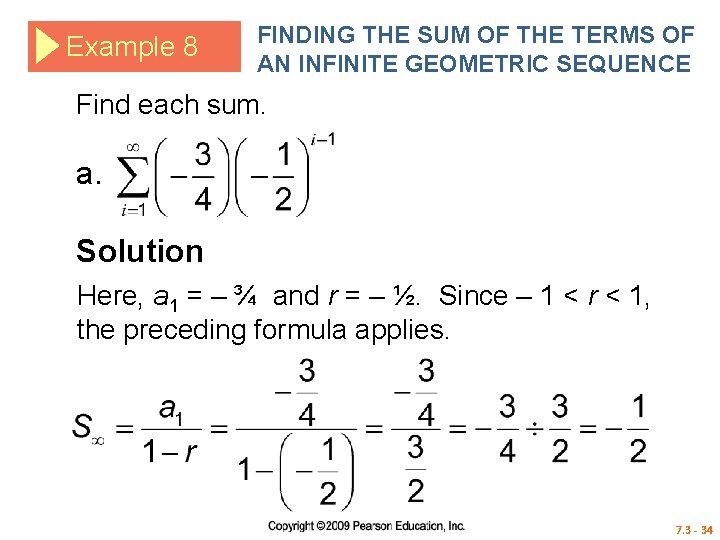
Example 8 FINDING THE SUM OF THE TERMS OF AN INFINITE GEOMETRIC SEQUENCE Find each sum. a. Solution Here, a 1 = – ¾ and r = – ½. Since – 1 < r < 1, the preceding formula applies. 7. 3 - 34

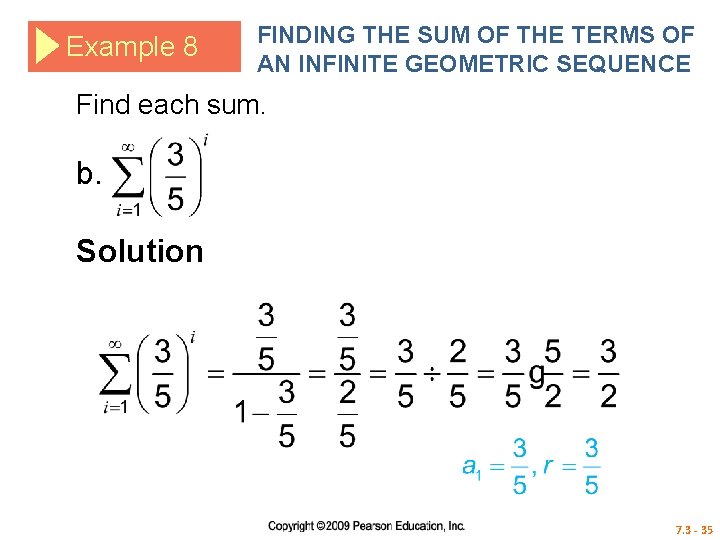
Example 8 FINDING THE SUM OF THE TERMS OF AN INFINITE GEOMETRIC SEQUENCE Find each sum. b. Solution 7. 3 - 35

Annuities A sequence of equal payments made after equal periods of time, such as car payments or house payments, is called an annuity. If the payments are accumulated in an account (with no withdrawals), the sum of the payments and interest on the payments is called the future value of the annuity. 7. 3 - 36

Example 9 FINDING THE FUTURE VALUE OF AN ANNUITY To save money for a trip, Taylor Wells deposited $1000 at the end of each year for 4 yr in an account paying 3% interest, compounded annually. Find the future value of this annuity. Solution To find the future value, we use the formula for interest compounded annually, 7. 3 - 37

Example 9 FINDING THE FUTURE VALUE OF AN ANNUITY The first payment earns interest for 3 yr, the second payment for 2 yr, and the third payment for 1 yr. The last payment earns no interest. The total amount is 7. 3 - 38

Example 9 FINDING THE FUTURE VALUE OF AN ANNUITY This is the sum of the terms of a geometric sequence with first term (starting at the end of the sum as written above) a 1 = 1000 and common ratio r = 1. 03. Using the formula for S 4, the sum of four terms, gives The future value of the annuity is $4183. 63. 7. 3 - 39

Future Value of an Annuity The formula for the future value of an annuity is given by where S is future value, R is payment at the end of each period, i is interest rate period, and n is number of periods. 7. 3 - 40