ARITHMETIC GEOMETRIC SEQUENCES Sequence Ellipsis Arithmetic sequence Geometric

ARITHMETIC & GEOMETRIC SEQUENCES Sequence Ellipsis Arithmetic sequence Geometric sequence

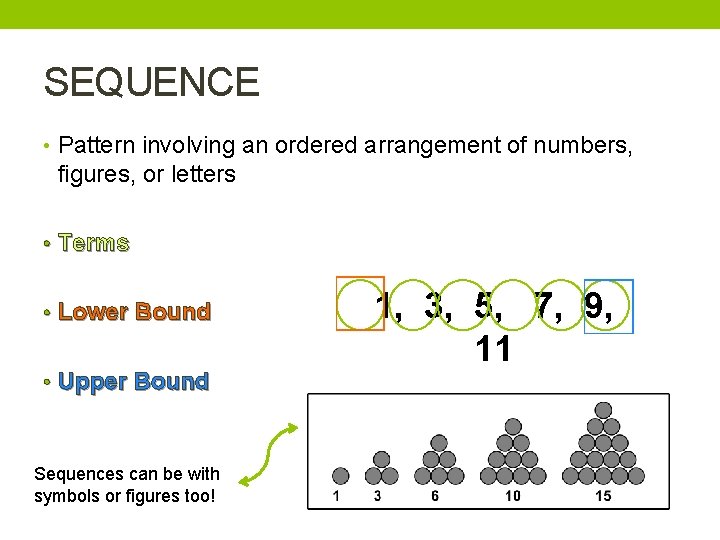
SEQUENCE • Pattern involving an ordered arrangement of numbers, figures, or letters • Terms • Lower Bound • Upper Bound Sequences can be with symbols or figures too! 1, 3, 5, 7, 9, 11

ELLIPSIS … • Sequences can be… FINITE or INFINITE • Finite: sequence terminates • Infinite: continues forever • Use ellipsis to signify infinite sequence 1, 2, 3, 4, 5, …

ARITHMETIC SEQUENCE • Sequence of terms, where the difference between Difference is usually referred to as consecutive terms stays constant Arithmetic Sequence Not Arithmetic Sequence “Common Difference” (d) +2 +3 d = -5 +4 d = undefined

ARITHMETIC SEQUENCE • Determine whether the sequences below are arithmetic or not Arithmetic Not Arithmetic

GEOMETRIC SEQUENCE • Sequence of terms, where the ratio between consecutive term stays constant • Ratio is usually referred to as “common ratio” (r) Geometric Sequence Not Geometric Sequence 1, 5, 25, 50, 250, … ✕ 2✕ 2✕ 2 ✕ 2 r=2 ✕ 5✕ 5 ✕ 2 ✕ 5 r = undefined

GEOMETRIC SEQUENCE • Determine whether the sequences below are geometric or not r=3 r = undefined Geometric 16, 8, 4, 1 Not Geometric r = -1/2 Geometric r = -2 Geometric

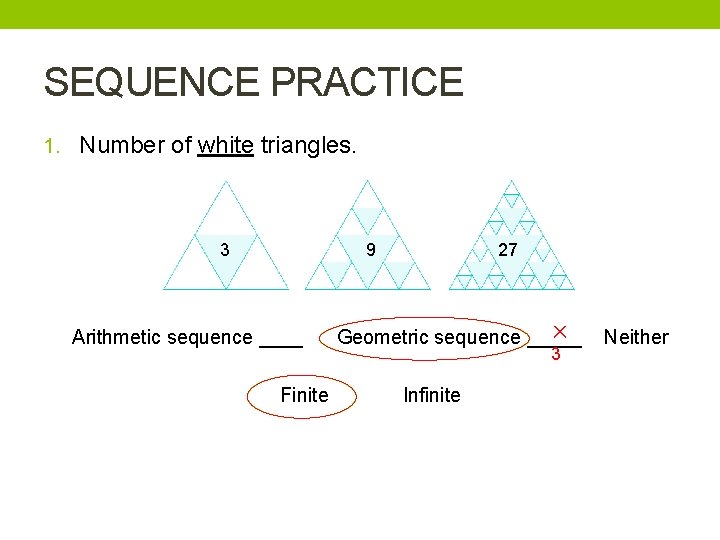
SEQUENCE PRACTICE 1. Number of white triangles. 3 9 Arithmetic sequence ____ Finite 27 ✕ Geometric sequence _____ 3 Infinite Neither

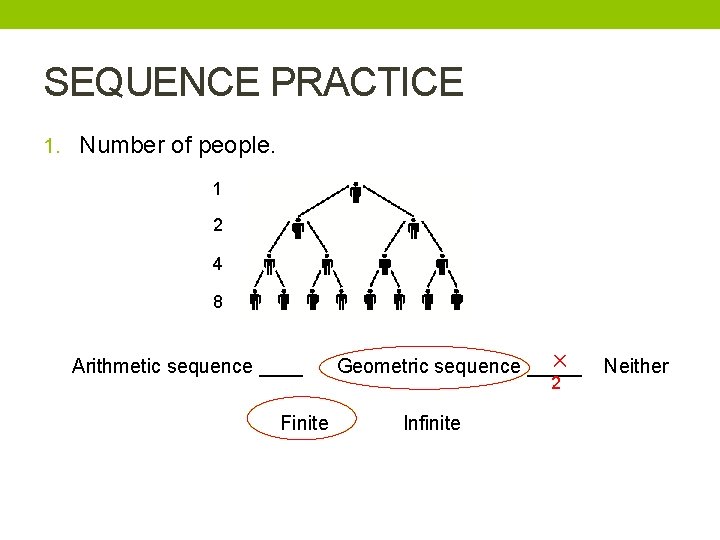
SEQUENCE PRACTICE 1. Number of people. 1 2 4 8 Arithmetic sequence ____ Finite ✕ Geometric sequence _____ 2 Infinite Neither

WORKSHEET TIME • Time for some extra practice. Answer the four questions on the worksheet to the best of your ability. • 8 min. time limit • ANSWERS: 1. Geometric sequence, *2, Finite 2. Neither, since it isn’t a sequence, the last sentence of the directions doesn’t apply 3. Geometric sequence, *2/3, Infinite 4. Arithmetic sequence, +3, Finite

ARITHMETIC EXPLICIT an = a 1 + d(n-1) Let’s take a simple arithmetic sequence for example: 1, 3, 5, 7 Now let’s label each term number: 1 2 3 4 1 3 5 7

ARITHMETIC EXPLICIT Let’s write out the sequence from the previous slide into a table for visual purposes: Term number x 1 2 3 4 Term value y 1 3 5 7 Therefore, we can rewrite the table into an equation: y = 2 x – 1 What is the value of the 4 th term in this sequence? y = 2(4) – 1 y=8– 1 y=7 An explicit formula defines the value at a specific position in an arithmetic sequence.

ARITHMETIC RECURSIVE Instead of using the relationship between the term number and term value, a recursive formula uses the relationship between a term value and the previous term’s value Term number x 1 2 3 4 Term value y 1 3 5 7 1 3 +2 Each term is the previous term PLUS the common difference!

RECURSIVE SEQUENCE What does this mean?

EXPLICIT OR RECURSIVE Explicit or Recursive? A. For this hour, Gerard is paid $10 more than what he was paid the previous hour. B. Gerard is paid $12. Answer: A = Recursive; B = Explicit or Recursive? A. I eat Cornflakes for breakfast. B. I place the toothpaste on my toothbrush before brushing my teeth. Answer: A = Explicit; B = Recursive

FORMULAS Explicit Formula Recursive Formula Arithmetic Sequence Geometric Sequence an = a 1 + d(n-1) gn = g 1 ✕ r(n-1) an = an-1 + d gn = gn-1 ✕ r

GEOMETRIC FORMULAS There is a slight difference between arithmetic and geometric sequences. Instead or d, we have r. Explicit: Recursive: gn = g 1 ✕ r(n-1) gn = gn-1 ✕ r x 1 2 3 y 3 9 27 The 3 rd term is 3 multiplied by 32. 3 * 9 = 27 The 2 nd term is 3 multiplied by 31. 3*3=9 The 3 rd term is the 2 nd term multiplied by the common ratio. 9 * 3 = 27