13 1 Arithmetic and Geometric Sequences ARITHMETIC SEQUENCES




















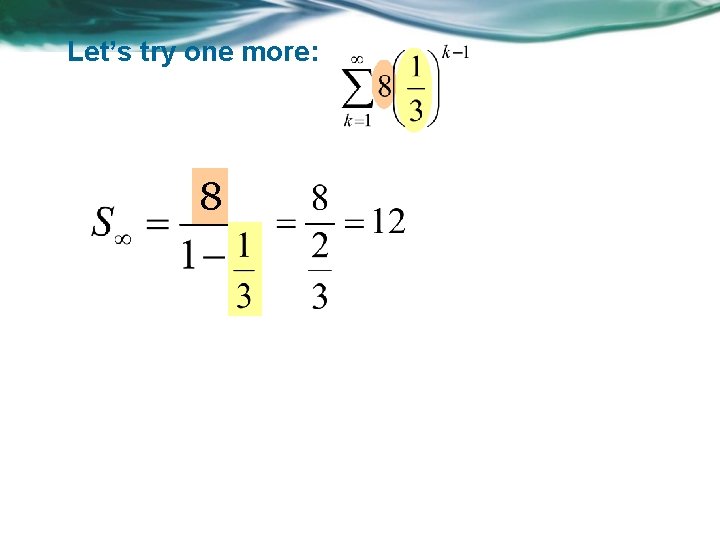





- Slides: 30

13 -1 Arithmetic and Geometric Sequences

ARITHMETIC SEQUENCES These are sequences where the difference between successive terms of a sequence is always the same number. This number is called the common difference.

NOTATION 1 st term = t₁ 2 nd term = t₂ 3 rd term = t₃ 4 th term = t₄ nth term = tn Some people use a to describe the terms of a sequence. However some prefer to use t.

3, 7, 11, 15, 19 … d = 4 a=3 Notice in this sequence that if we find the difference between any term and the term before it we always get 4. 4 is then called the common difference and is denoted with the letter d. To get to the next term in the sequence we would add 4 so a recursive formula for this sequence is: The first term in the sequence would be a 1 which is sometimes just written as a.

+4 +4 d=4 3, 7, 11, 15, 19 … Each time you want another term in the sequence you’d add d. This would mean the second term was the first term plus d. The third term is the first term plus d (added twice). The fourth term is the first term plus d (added three times). So you can see to get the nth term we’d take the first term and add d (n - 1) times. Try this to get the 5 th term.

Let’s look at a formula for an arithmetic sequence and see what it tells us. We can think of this as a “compensating term”. Without it the sequence would start at 4 but this gets it started where we want it. you can see what the common difference will be in the formula Subbing in the set of positive integers we get: 3, 7, 11, 15, 19, … What is the common difference? 4 n would generate the multiples of 4. With the - 1 on the end, everything is back one. What would you do if you wanted the sequence 2, 6, 10, 14, 18, . . . ? d=4

Find the nth term of the arithmetic sequence when a = 6 and d = -2 If we use -2 n we will generate a sequence whose common difference is -2, but this sequence starts at -2 (put 1 in for n to get first term to see this). We want ours to start at 6. We then need the “compensating term”. If we are at -2 but want 6, we’d need to add 8. Check it out by putting in the first few positive integers and verifying that it generates our sequence. Sure enough---it starts at 6 and has a common difference of -2 6, 4, 2, 0, -2, . . .

Let’s try something a little trickier. What if we just know a couple of terms and they aren’t consecutive? The fourth term is 3 and the 20 th term is 35. Find the first term and both a term generating formula and a recursive formula for this sequence. How many differences would you add to get from the 4 th term to the 20 th term? 35 3 Solve this for d The fourth term is the first term plus 3 common differences. 3 d=2 (2) We have all the info we need to express these sequences. We’ll do it on next slide.

The fourth term is 3 and the 20 th term is 35. Find the first term and both a term generating formula and a recursive formula for this sequence. d=2 makes the first term - 3 instead of 2 makes the common difference 2 Let’s check it out. If we find n = 4 we should get the 4 th term and n = 20 should generate the 20 th term. The recursive formula would be:

The fourth term is 3 and the 20 th term is 35. Find the first term and both a term generating formula and a recursive formula for this sequence. Another method

Often in applications we will want the sum of a certain number of terms in an arithmetic sequence. The story is told of a grade school teacher In the 1700's that wanted to keep her class busy while she graded papers so she asked them to add up all of the numbers from 1 to 100. These numbers are an arithmetic sequence with common difference 1. Carl Friedrich Gauss was in the class and had the answer in a minute or two (remember no calculators in those days). This is what he did: sum is 101 1 + 2 + 3 + 4 + 5 +. . . + 96 + 97 + 98 + 99 + sum is 101 100 With 100 numbers there are 50 pairs that add up to 101. 50(101) = 5050

This will always work with an arithmetic sequence. The formula for the sum of n terms is: n is the number of terms so n/2 would be the number of pairs first term last term Let’s find the sum of 1 + 3 +5 +. . . + But how 59 many terms are there? We can write a formula for the sequence and then figure out what term number 59 is.

first term last term Let’s find the sum of 1 + 3 +5 +. . . + 59 The common difference is 2 and the first term is one so: Set this equal to 59 to find n. Remember n is the term number. 2 n - 1 = 59 n = 30 So there are 30 terms to sum up.

GEOMETRIC SEQUENCES These are sequences where the ratio of successive terms of a sequence is always the same number. This number is called the common ratio.

1, 2, 4, 8, 16. . . r=2 Notice in this sequence that if we find the ratio of any term to the term before it (divide them) we always get 2. 2 is then called the common ratio and is denoted with the letter r. To get to the next term in the sequence we would multiply by 2 so a recursive formula for this sequence is:

2 2 1, 2, 4, 8, 16. . . r=2 a=1 Each time you want another term in the sequence you’d multiply by r. This would mean the second term was the first term times r. The third term is the first term multiplied by r (r squared). The fourth term is the first term multiplied by r (r cubed). So you can see to get the nth term we’d take the first term and multiply r (n - 1) times. Try this to get the 5 th term.

Let’s look at a formula for a geometric sequence and see what it tells us. you can see what the common ratio will be in the formula This factor gets us started in the right place. With n = 1 we’d get -2 for the first term Subbing in the set of positive integers we get: -2, -6, -18, -54 … What is the common ratio? 3 n-1 would generate the powers of 3. With the - 2 in front, the first term would be -2(30) =- 2. What would you do if you wanted the sequence -4, -12, -36, -108, . . . ? r=3

Find the nth term of the geometric sequence when a = -2 and r =4 If we use 4 n-1 we will generate a sequence whose common ratio is 4, but this sequence starts at 1 (put 1 in for n to get first term to see this). We want ours to start at -2. We then need the “compensating factor”. We need to multiply by -2. Check it out by putting in the first few positive integers and verifying that it generates our sequence. Sure enough---it starts at -2 and has a common ratio of 4 -2, -8, -32, -128, . . .

Find the 8 th term of 0. 4, 0. 04. 0. 004, . . . To find the common ratio, take any term and divide it by the term in front

If we want to add n terms in a geometric sequence, we use the formula below: number of terms first term sum of n terms common ratio Find the sum: 4 + 12 + 36 + 108 +. . . + 4(3)14= 28, 697, 812

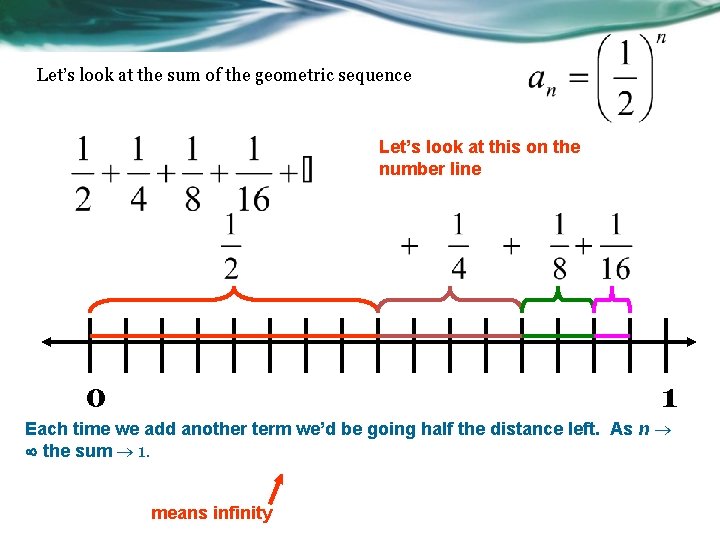
Let’s look at the sum of the geometric sequence Let’s look at this on the number line 0 1 Each time we add another term we’d be going half the distance left. As n the sum 1. means infinity

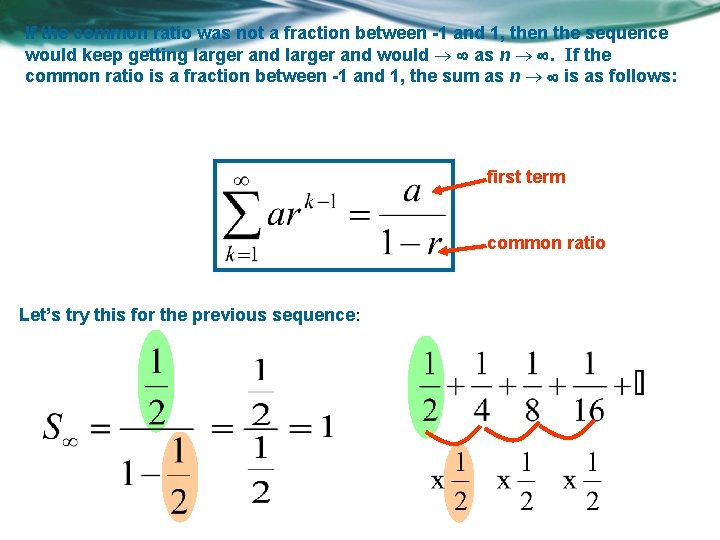
If the common ratio was not a fraction between -1 and 1, then the sequence would keep getting larger and would as n . If the common ratio is a fraction between -1 and 1, the sum as n is as follows: first term common ratio Let’s try this for the previous sequence:
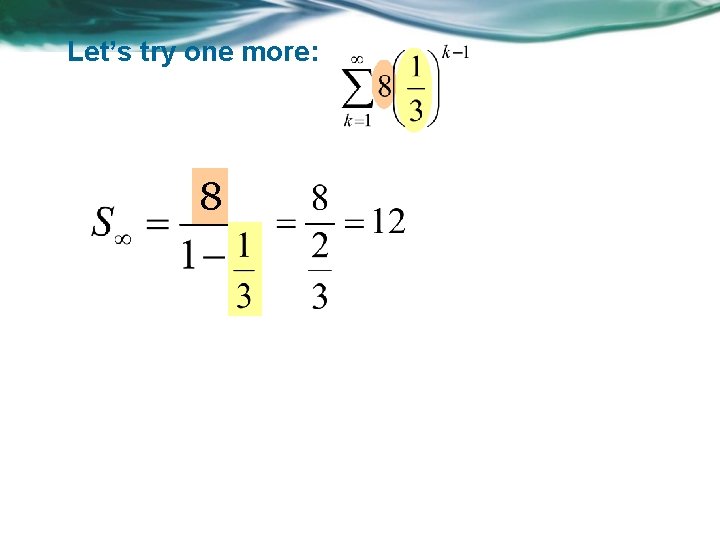
Let’s try one more: 8

Example 1

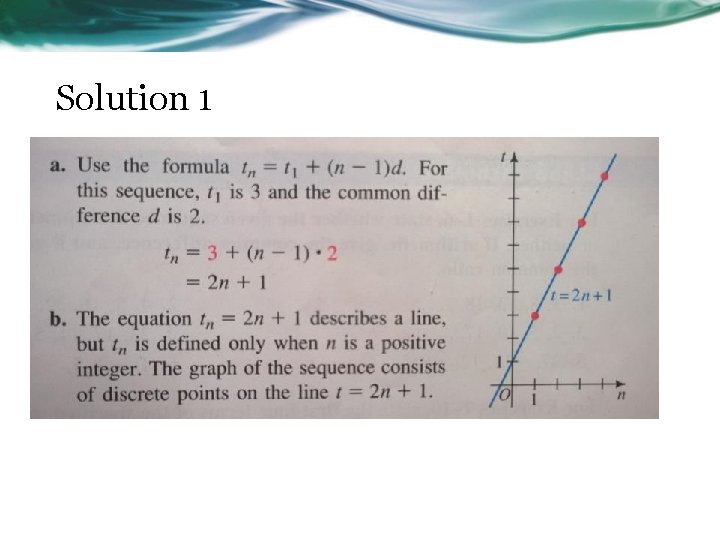
Solution 1

Example 2

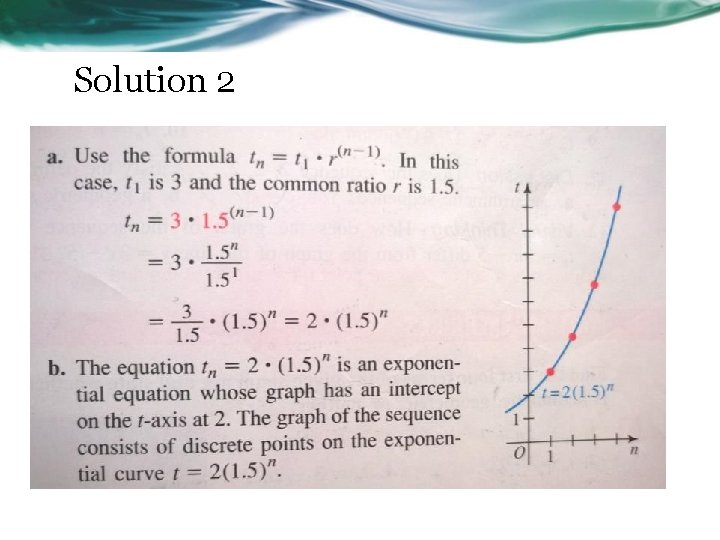
Solution 2

Example 3

Solution 3

Homework Written exercises on Page 476: