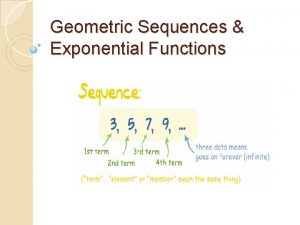
Arithmetic Sequences and Series Geometric Where do I

Arithmetic Sequences and Series Geometric Where do I belong? Pg. 607 #1 -32

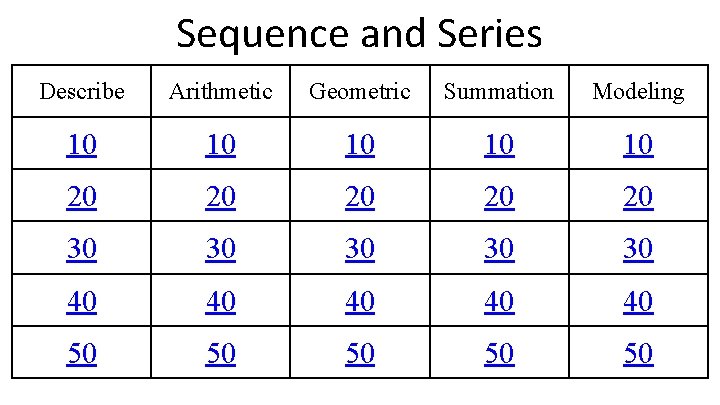
Sequence and Series Describe Arithmetic Geometric Summation Modeling 10 10 10 20 20 20 30 30 30 40 40 40 50 50 50

Describe each using: Sequence/Series; Arithmetic/Geometric; Finite/Infinite 2, 8, 14, 20, 26 Answer

Describe each using: Sequence/Series; Arithmetic/Geometric; Finite/Infinite 2, 8, 14, 20, 26 Finite Arithmetic Sequence

Describe each using: Sequence/Series; Arithmetic/Geometric; Finite/Infinite 2, 8, 32, 128, … Answer

Describe each using: Sequence/Series; Arithmetic/Geometric; Finite/Infinite 2, 8, 32, 128, … Infinite Geometric Sequence

Describe each using: Sequence/Series; Arithmetic/Geometric; Finite/Infinite 1 + 5 + 9 + ∙∙∙ Answer

Describe each using: Sequence/Series; Arithmetic/Geometric; Finite/Infinite 1 + 5 + 9 + ∙∙∙ Infinite Arithmetic Series

Describe each using: Sequence/Series; Arithmetic/Geometric; Finite/Infinite 16 + 8 + 4 + 2 + 1 Answer

Describe each using: Sequence/Series; Arithmetic/Geometric; Finite/Infinite 16 + 8 + 4 + 2 + 1 Finite Geometric Series

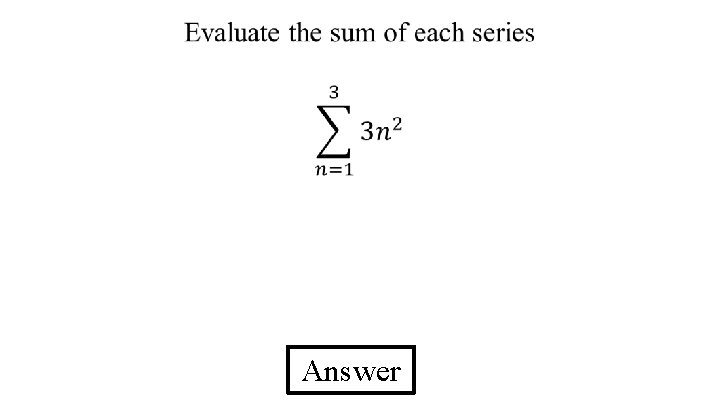
Answer

Infinite Geometric Series

Answer

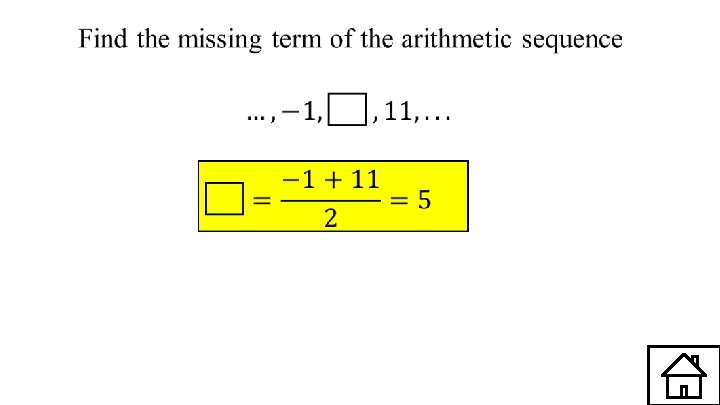
Write a recursive definition, explicit formula and find the 15 term for the sequence: 12, 21, 30, 39, . . . Answer

Write a recursive definition, explicit formula and find the 15 term for the sequence: 12, 21, 30, 39, . . .

Write a recursive definition, explicit formula and find the 18 term for the sequence: 45, 37, 29, 21, . . . Answer

Write a recursive definition, explicit formula and find the 18 term for the sequence: 45, 37, 29, 21, . . .

Answer

Answer

Answer

Answer

Answer

Answer

Answer

Answer

Answer

Answer

Answer

Answer

The number of toy rockets made by an assembly line for 8 hours forms an arithmetic sequence. If the line produced 40 rockets in hour one and 43 rockets in hour two, how many rockets will be produced in hour seven? How many rockets will be produced in one 8 hour day? Answer

The number of toy rockets made by an assembly line for 8 hours forms an arithmetic sequence. If the line produced 40 rockets in hour one and 43 rockets in hour two, how many rockets will be produced in hour seven? How many rockets will be produced in one 8 hour day?

You invested money in a fund and each month you receive a payment for your investment. Over the first four months, you received $50, $57, $64, $71. If this pattern continues, how much will you receive in the 12 th month and who much will you receive for the entire year? Write an explicit equation to model the problem. Answer

You invested money in a fund and each month you receive a payment for your investment. Over the first four months, you received $50, $57, $64, $71. If this pattern continues, how much will you receive in the 12 th month and who much will you receive for the entire year? Write an explicit equation to model the problem.

You are trying to save $1500. You begin with $5 and save $3 more than the previous week for 30 weeks. Will you meet your goal? • Write an explicit formula to model this problem • What is the amount you will save in week 30? • What is the total amount you will save over 30 weeks? Answer

You are trying to save $1500. You begin with $5 and save $3 more than the previous week for 30 weeks. Will you meet your goal? No • Write an explicit formula to model this problem • What is the amount you will save in week 30? • What is the total amount you will save over 30 weeks?

You saved $500 this year. Each year you plan to save 5% more than the previous year. Write an explicit formula to model this situation. How much will you save in the 8 year? How much will you have saved totally over years, assume you do not spend anything? Answer

You saved $500 this year. Each year you plan to save 5% more than the previous year. Write an explicit formula to model this situation. How much will you save in the 8 year? How much will you have saved totally over years, assume you do not spend anything?

You drop a ball from a staircase that is 36 feet high. By the time you get down the stairs to measure the height of the bounce, the ball has bounced four times and has a height of 2. 25 feet after its fourth bounce. How high did the ball bounce after it first hit the floor? (hint the bouncing ball creates a geometric sequence) Answer

You drop a ball from a staircase that is 36 feet high. By the time you get down the stairs to measure the height of the bounce, the ball has bounced four times and has a height of 2. 25 feet after its fourth bounce. How high did the ball bounce after it first hit the floor?