LESSON 10 2 Arithmetic Sequences and Series FiveMinute

LESSON 10– 2 Arithmetic Sequences and Series

Five-Minute Check (over Lesson 10 -1) TEKS Then/Now New Vocabulary Example 1: Arithmetic Sequences Key Concept: The nth Term of an Arithmetic Sequence Example 2: Explicit and Recursive Formulas Example 3: nth Terms Example 4: Arithmetic Means Example 5: Second Differences Key Concept: Sum of a Finite Arithmetic Series Example 6: Sums of Arithmetic Series Example 7: Real-World Example: Sum of an Arithmetic Series Example 8: Real-World Example: Sum of an Arithmetic Series

Over Lesson 10 -1 Find the next four terms of the sequence 2, 5, 8, 11, …. A. 13, 15, 17, 19 B. 14, 17, 20, 23 C. 15, 19, 23, 27 D. 15, 20, 26, 33

Over Lesson 10 -1 Find the next four terms of the sequence 3, − 9, 27, − 81, …. A. 162, – 324, 648, – 1296 B. 243, – 729, 2187, – 6561 C. 243, 729, 2187, 6561 D. 324, – 1296, 5184, – 20, 736

Over Lesson 10 -1 Find the third term of the sequence a 1 = 10, an = – 2 an– 1 + 4. A. a 3 = – 68 B. a 3 = – 16 C. a 3 = 36 D. a 3 = 76

Over Lesson 10 -1 Find the sixth term of the sequence an = A. a 6 = B. a 6 = C. a 6 = D. a 6 = 3 .

Over Lesson 10 -1 Find A. 8 B. 23 C. 50 D. 90 .

Over Lesson 10 -1 Which of the following sequences is divergent? A. 3, 11, 15, 17, … B. 9, 7, 5, 3, … C. 20, − 5, 1. 25, – 0. 3125, … D. 32, 16, 8, 4, …

Targeted TEKS P. 5(C) Calculate the n th term and the n th partial sum of an arithmetic series in mathematical and realworld problems. P. 5(D) Represent arithmetic series and geometric series using sigma notation. Also addresses P. 5(A) and P. 5(B). Mathematical Processes P. 1(B), P. 1(G)

You found terms of sequences and sums of series. (Lesson 10 -1) • Find nth terms and arithmetic means of arithmetic sequences. • Find sums of n terms of arithmetic series.

• arithmetic sequence • common difference • arithmetic means • first difference • second difference • arithmetic series

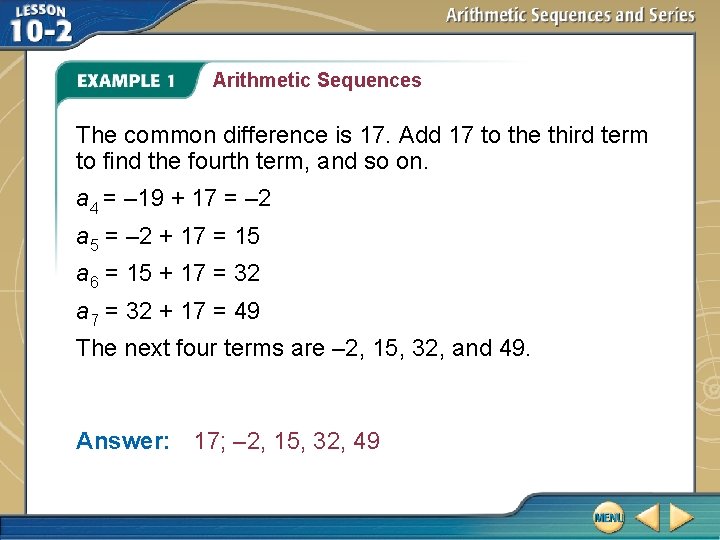
Arithmetic Sequences Determine the common difference and the next four terms of the arithmetic sequence – 53, – 36, – 19, …. First, find the common difference. a 2 a 1 = – 36 – (– 53) or 17 a 3 a 2 = – 19 – (– 36) or 17 Find the difference between pairs of consecutive terms to determine the common difference.

Arithmetic Sequences The common difference is 17. Add 17 to the third term to find the fourth term, and so on. a 4 = – 19 + 17 = – 2 a 5 = – 2 + 17 = 15 a 6 = 15 + 17 = 32 a 7 = 32 + 17 = 49 The next four terms are – 2, 15, 32, and 49. Answer: 17; – 2, 15, 32, 49

Determine the common difference and find the next four terms of the arithmetic sequence 74, 68, 62, 56, …. A. – 6; 50, 44, 38, 32 B. – 5; 51, 46, 41, 36 C. – 4; 52, 48, 44, 40 D. 6; 62, 68, 74, 80

Explicit and Recursive Formulas Find both an explicit formula and a recursive formula for the nth term of the arithmetic sequence 14, 3, – 8, …. First, find the common difference. a 2 a 1 = 3 14 or 11 a 3 a 2 = 8 3 or 11 Find the difference between pairs of consecutive terms to determine the common difference.

Explicit and Recursive Formulas For an explicit formula, substitute a 1 = 14 and d = – 11 in the formula for the nth term of an arithmetic sequence. an = a 1 + (n 1)d nth term of an arithmetic sequence = 14 + (n 1)( 11) a 1 =14 and d = – 11 = 14 + ( 11)(n 1) or – 11 n + 25 Simplify.

Explicit and Recursive Formulas For a recursive formula, state the first term a 1 and then indicate that the next term is the sum of the previous term an 1 and d. a 1 = 14 an = an 1 + ( 11) or an = an 1 – 11 An explicit formula for the sequence is an = 14 + ( 11)(n 1) or an = – 11 n +25, and a recursive formula is a 1 = 14, an = an 1 – 11. Answer: an = 14 + (– 11)(n – 1) or an = – 11 n + 25; a 1 = 14, an = an – 11

Find both an explicit formula and a recursive formula for the nth term of the arithmetic sequence 15, 33, 51, …. A. an = 15 n; a 1 = 15, an = an – 1 + 18 B. an = 15 n; a 1 = 18, an = an – 1 + 15 C. an = 18 n – 3; a 1 = 15, an = an – 1 + 18 D. an = 18 n; a 1 = 15, an = an – 1 + 18

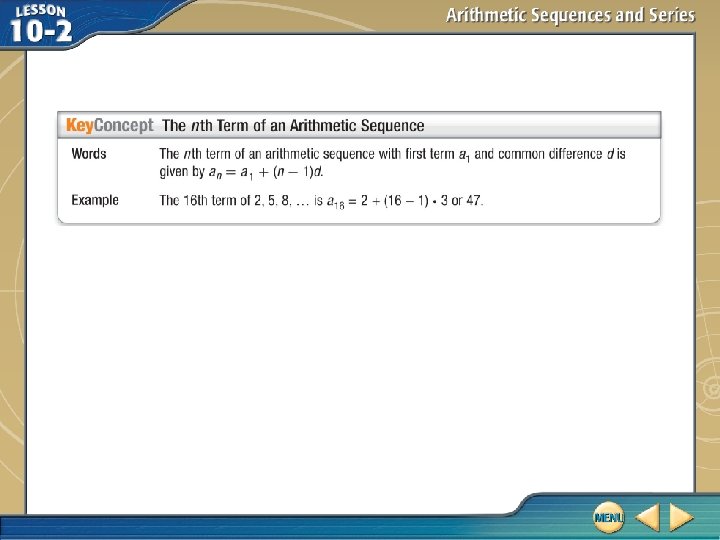
nth Terms A. Find the 41 st term of the arithmetic sequence 11, 4, – 3, – 10, …. First, find the common difference. a 2 – a 1 = 4 – 11 or – 7 a 3 – a 2 = – 3 – 4 or – 7 Find the difference between pairs of consecutive terms to determine the common difference.

nth Terms Use the formula for the nth term of an arithmetic sequence to find a 41. an = a 1 + (n – 1)d nth term of an arithmetic sequence a 41 = 11 + (41 – 1)(– 7) n = 41, a 1 = 11, and d = – 7 a 41 = – 269 Simplify. The 41 st term of the sequence is – 269. Answer: – 269

nth Terms B. Find the first term of the arithmetic sequence for which a 44 = 229 and d = 8. Use the formula for the nth term of an arithmetic sequence. an = a 1 + (n 1)d 229 = a 1 + (44 1)8 a 1 = – 115 nth term of an arithmetic sequence n = 44, an = 229, and d = 8 Simplify. The first term of the sequence is – 115. Answer: – 115

Find the 25 th term of the arithmetic sequence 49, 40, 31, …. A. – 176 B. – 167 C. – 158 D. 265

Arithmetic Means Write an arithmetic sequence that has five arithmetic means between 6. 2 and – 1. 6. ? , The sequence will resemble 6. 2, _____ ? , – 1. 6. Note that – 1. 6 is the 7 th ? , _____ term of the sequence or a 7. First, find the common difference using a 7 = – 1. 6, a 1 = 6. 2, and n = 7. an = a 1 + (n 1)d – 1. 6 = 6. 2 + (7 – 1)d nth term of an arithmetic sequence an = – 1. 6, a 1 = 6. 2, and n = 7

Arithmetic Means – 1. 6 = 6. 2 + 6 d d = – 1. 3 Simplify. Solve for d. Then determine the arithmetic means by using d = – 1. 3. a 2 = 6. 2 + (– 1. 3) or 4. 9 a 3 = 4. 9 + (– 1. 3) or 3. 6 a 4 = 3. 6 + (– 1. 3) or 2. 3 a 5 = 2. 3 + (– 1. 3) or 1 a 6 = 1 + (– 1. 3) or – 0. 3 The sequence is 6. 2, 4. 9, 3. 6, 2. 3, 1, – 0. 3, – 1. 6. Answer: 6. 2, 4. 9, 3. 6, 2. 3, 1, – 0. 3, – 1. 6

Write an arithmetic sequence that has five arithmetic means between 16. 2 and 14. 7. A. 16. 2, 15. 825, 15. 45, 15. 075, 14. 7 B. 16. 2, 16. 0, 15. 7, 15. 5, 15. 3, 15. 0, 14. 7 C. 16. 2, 15. 95, 15. 7, 15. 45, 15. 2, 14. 95, 14. 7 D. 16. 2, 16. 0, 15, 8, 15. 6, 15, 4, 15, 2, 15, 14. 7

Second Differences Find a quadratic model for the sequence 0, 5, 12, 21, 32, 45, …. The nth term can be represented by a quadratic equation of the form an = an 2 + bn + c. Substitute values for an and n into the equation. 0 = a(1)2 + b(1) + c an = 0 and n = 1 5 = a(2)2 + b(2) + c an = 5 and n = 2 12 = a(3)2 + b(3) + c an = 12 and n = 3 This yields a system of linear equations in three variables.

Second Differences 0 =a+b+c Simplified first equation 5 = 4 a + 2 b + c Simplified second equation 12 = 9 a + 3 b + c Simplified third equation Solving for a, b, and c, gives a = 1, b = 2, and c = – 3. Substituting these values in the equation for an, the model for the sequence is an = n 2 + 2 n – 3, as shown in the graph below.

Second Differences Answer: an = n 2 + 2 n – 3

Find a quadratic model for the sequence 10, 14, 22, 34, 50, …. A. an = n 2 – 2 n + 11 B. an = 2 n 2 – 2 n + 10 C. an = 4 n 2 – 2 n + 8 D. an = 10 n 2 + 10

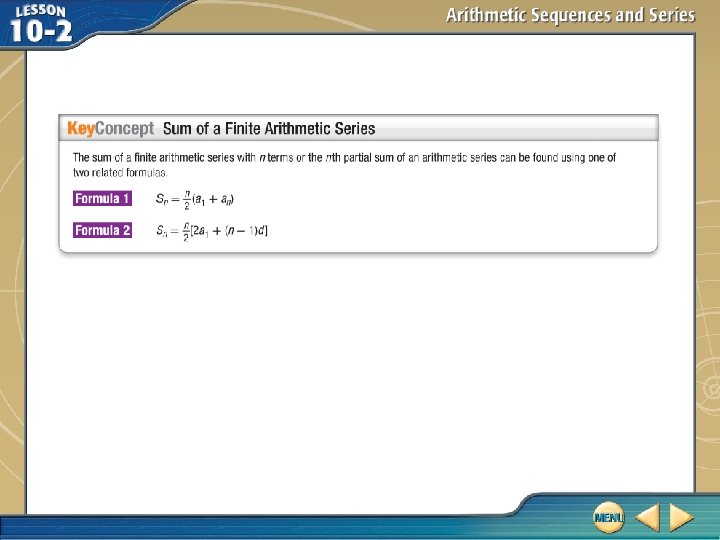
Sums of Arithmetic Series A. Find the sum of – 3 + 2 + 7 + 12 + … + 157. In this sequence, a 1 = – 3, an = 157, and d = 2 – (– 3) or 5. Use the nth term formula to find the number of terms in the sequence n. an = a 1 + (n – 1)d nth term of an arithmetic sequence 157 = – 3 + (n – 1)5 an = 157, a 1 = – 3, d = 5 33 = n Now use the formula the series. Simplify. to find the sum of

Sums of Arithmetic Series Sum of an arithmetic series formula 1. n = 33, a 1 = 3, an = 157 = 2541 Answer: 2541 Simplify.

Sums of Arithmetic Series B. Find the 17 th partial sum of the arithmetic series 53 + 31 + 9 + …. In this sequence, a 1 = 53 and d = 31 – 53 or – 22. Use Formula 2 to find the 17 th partial sum. Sum of an arithmetic series formula 2. n = 17, a 1 = 53, d = – 22 = – 2091 Answer: – 2091 Simplify.

Sums of Arithmetic Series C. = (10 + 6) + (11 + 6) + ··· + (32 + 6) = 16 + 17 + ··· + 38 The first term of this series is 16, and the last term is 38. The number of terms is equal to the upper bound minus the lower bound plus one, which is 32 – 10 + 1, or 23. Therefore, a 1 = 16, an = 38, and n = 23. Use Formula 1 to find the sum of the series.

Sums of Arithmetic Series Sum of an arithmetic series formula 1. n = 23, a 1 = 16, an = 38 = 621 Answer: 621 Simplify.

Find A. 2072 B. 2146 C. 4144 D. 4292 .

Sum of Arithmetic Series MUSIC An artist receives royalties for all CDs of his music that are sold. For the first 10, 000 CDs sold, the artist receives $10, 000. He receives $12, 500 for the next 10, 000 CDs, $15, 000 for the next 10, 000 CDs, and so on. How much money will he receive if 500, 000 of his CDs are sold? First, find the number of terms in the series. Since the artist is paid for every 10, 000 CDs, the number of terms is 500, 000 10, 000 = 50. In this sequence, a 1 = 10, 000 and d = 12, 500 – 10, 000 or 2500. Use Formula 2 to find the sum of the series.

Sum of Arithmetic Series Formula 2 n = 50, a 1 =10, 000, d = 2500 = 3, 562, 500 Simplify. He will receive $3, 562, 500 if 500, 000 of his CDs are sold. Answer: $3, 562, 500

PROFIT The profit a shoe manufacturer makes depends on how many pairs of shoes are sold. For the first 1000 pairs sold, the manufacturer makes $4000 in profit. His profit is $6000 for the next 1000 pairs, $8000 for the next 1000 pairs, and so on. How much profit will the manufacturer make if he sells 20, 000 pairs of shoes? A. $46, 000 B. $420, 000 C. $460, 000 D. $480, 000

Sum of an Arithmetic Series SALES Anna sells clothing in a store at a mall. Her commission on the sale of new seasonal merchandise is $3. 50 per item costing at least $25. To encourage an increase in sales, the store manager promises a $0. 05 increase in commission for each additional item sold. Thus, on the sale of the next item, Anna will earn $3. 55 in commission. On the sale of the third item, Anna will earn $3. 60, and so on. How many items worth $25 or more will Anna need to sell for her total commission on new merchandise to be at least $1000?

Sum of an Arithmetic Series Formula 2 Sn = 1000, a 1 =3. 50, d = 0. 05 Multiply each side by 2 and simplify. Distribute and subtract 2000 from each side. Divide each side by 0. 05.

Sum of an Arithmetic Series Use the Quadratic Formula. Simplify. Because items cannot be negative, Anna will need to sell at least 143 items worth $25 to receive at least $1000 in commission. Answer: At least 143 items

Sum of an Arithmetic Series CHECK $3. 50 + $3. 55 + $3. 60 + … + $10. 60 = = 1008. 15 After selling 143 items worth $25 or more, Anna will receive $1008. 15 in commission, which is more than $1000.

SALES A toy manufacturer wants to make a profit of $50, 000 the first year, $62, 000 the second year, $74, 000 the third year, and so on. His goal is to make a profit of at least $500, 000 per year selling toys. How many years will it take for the manufacturer to reach his goal? A. 6 B. 7 C. 10 D. 13

LESSON 10– 2 Arithmetic Sequences and Series