12 1 Arithmetic Sequences and Series An introduction

























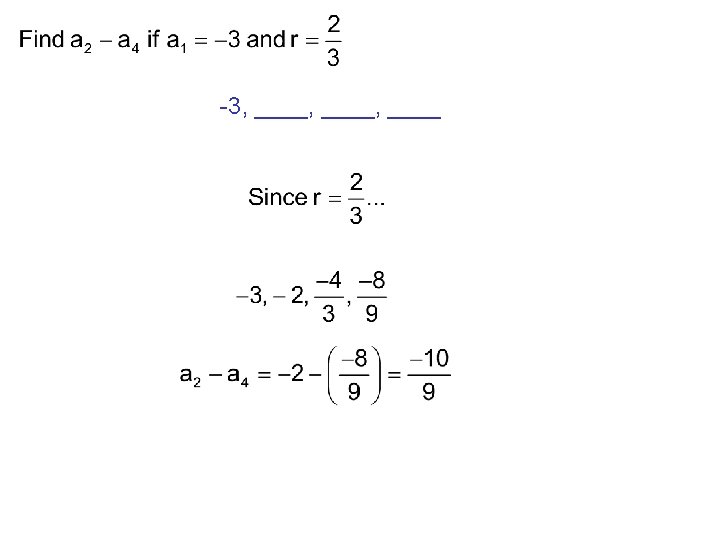












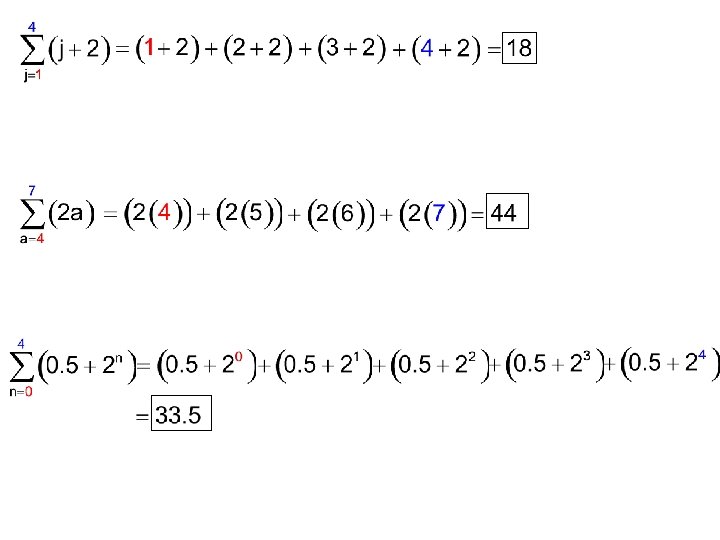
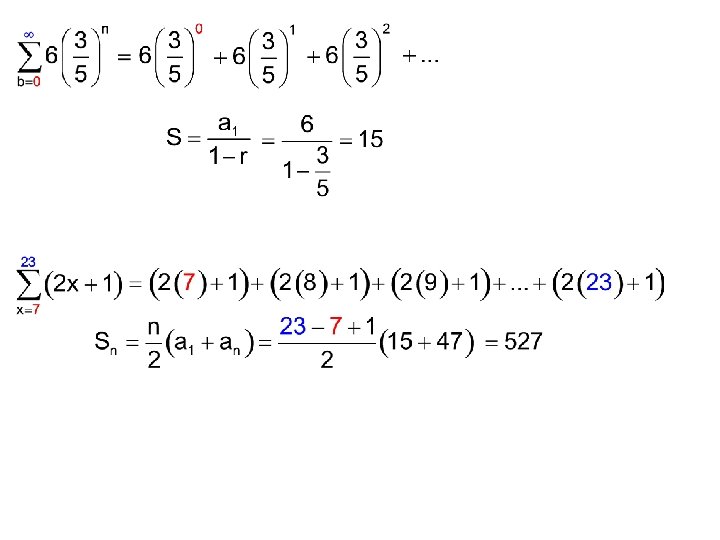





- Slides: 50

12. 1 – Arithmetic Sequences and Series

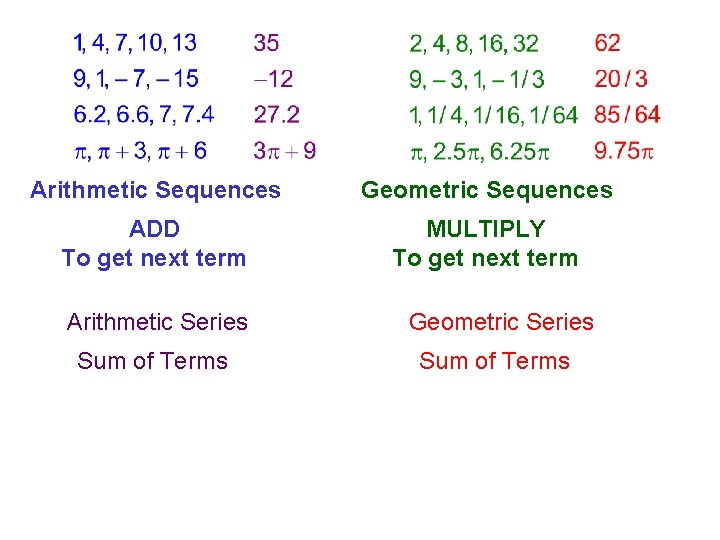
An introduction………… Arithmetic Sequences Geometric Sequences ADD To get next term MULTIPLY To get next term Arithmetic Series Geometric Series Sum of Terms

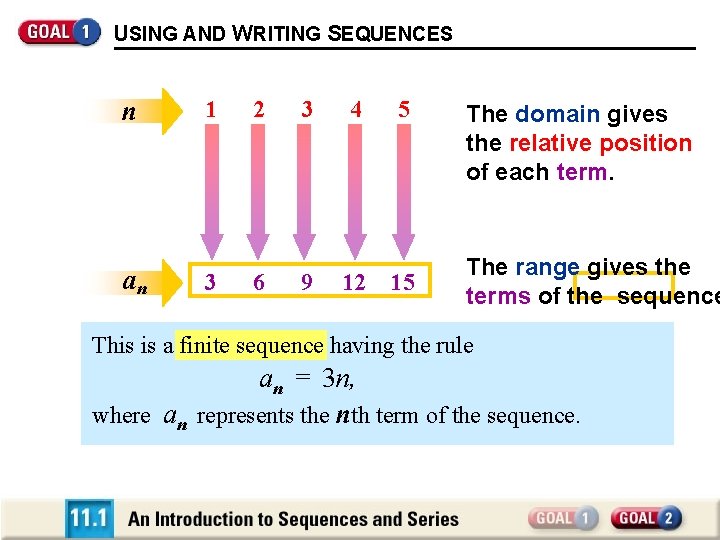
USING AND WRITING SEQUENCES The numbers in sequences are called terms. You can think of a sequence as a function whose domain is a set of consecutive integers. If a domain is not specified, it is understood that the domain starts with 1.

USING AND WRITING SEQUENCES DOMAIN: n an RANGE: 1 3 2 6 3 9 4 12 5 15 The domain gives the relative position of each term. The range gives the terms of the sequence This is a finite sequence having the rule an = 3 n, where an represents the nth term of the sequence.

Writing Terms of Sequences Write the first six terms of the sequence an = 2 n + 3. SOLUTION a 1 = 2(1) + 3 = 5 1 st term a 2 = 2(2) + 3 = 7 2 nd term a 3 = 2(3) + 3 = 9 3 rd term a 4 = 2(4) + 3 = 11 4 th term a 5 = 2(5) + 3 = 13 5 th term a 6 = 2(6) + 3 = 15 6 th term

Writing Terms of Sequences Write the first six terms of the sequence f (n) = (– 2) n – 1. SOLUTION f (1) = (– 2) 1 – 1 = 1 1 st term f (2) = (– 2) 2 – 1 = – 2 2 nd term f (3) = (– 2) 3 – 1 = 4 3 rd term f (4) = (– 2) 4 – 1 = – 8 4 th term f (5) = (– 2) 5 – 1 = 16 5 th term f (6) = (– 2) 6 – 1 = – 32 6 th term

Arithmetic Sequences How do I define an arithmetic sequence and how do I use the formula to find different terms of the sequence?

Arithmetic Sequences and Series Arithmetic Sequence: sequence whose consecutive terms have a common difference. Example: 3, 5, 7, 9, 11, 13, . . . The terms have a common difference of 2. The common difference is the number d. To find the common difference you use an+1 – an Example: Is the sequence arithmetic? – 45, – 30, – 15, 0, 15, 30 Yes, the common difference is 15 How do you find any term in this sequence? To find any term in an arithmetic sequence, use the formula an = a 1 + (n – 1)d where d is the common difference.

Find the 14 th term of the arithmetic sequence 4, 7, 10, 13, ……

In the arithmetic sequence 4, 7, 10, 13, …, which term has a value of 301?

Find the next four terms of – 9, -2, 5, … Arithmetic Sequence 7 is referred to as the common difference (d) Common Difference (d) – what we ADD to get next term Next four terms…… 12, 19, 26, 33

Find the next four terms of 0, 7, 14, … Arithmetic Sequence, d = 7 21, 28, 35, 42 Find the next four terms of x, 2 x, 3 x, … Arithmetic Sequence, d = x 4 x, 5 x, 6 x, 7 x Find the next four terms of 5 k, -7 k, … Arithmetic Sequence, d = -6 k -13 k, -19 k, -25 k, -32 k

Vocabulary of Sequences (Universal)

Given an arithmetic sequence with x 38 15 NA -3 X = 80

-19 353 ? ? 63 x 6

Try this one: 1. 5 x 16 NA 0. 5

9 633 x NA 24 X = 27

-6 20 29 NA x

Find two arithmetic means between – 4 and 5 -4, ____, 5 -4 5 4 NA x The two arithmetic means are – 1 and 2, since – 4, -1, 2, 5 forms an arithmetic sequence

Find three arithmetic means between 1 and 4 1, ____, 4 1 4 5 NA x The three arithmetic means are 7/4, 10/4, and 13/4 since 1, 7/4, 10/4, 13/4, 4 forms an arithmetic sequence

Find n for the series in which 5 y x 440 3 Graph on positive window X = 16

12. 2 – Geometric Sequences and Series

Arithmetic Sequences Geometric Sequences ADD To get next term MULTIPLY To get next term Arithmetic Series Geometric Series Sum of Terms

Vocabulary of Sequences (Universal)

Find the next three terms of 2, 3, 9/2, ___, ___ 3 – 2 vs. 9/2 – 3… not arithmetic

1/2 x 9 NA 2/3

Find two geometric means between – 2 and 54 -2, ____, 54 -2 54 4 NA x The two geometric means are 6 and -18, since – 2, 6, -18, 54 forms an geometric sequence
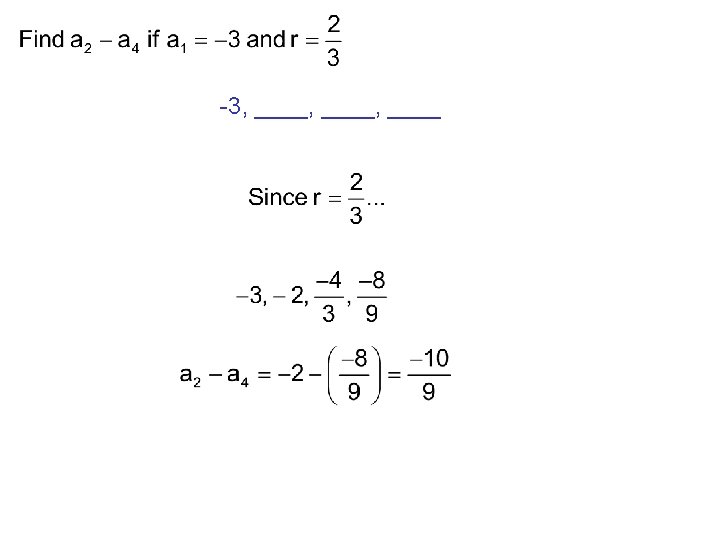

x 9 NA

x 5 NA

*** Insert one geometric mean between ¼ and 4*** denotes trick question 1/4 3 NA

1/2 7 x

Section 12. 3 – Infinite Series

1, 4, 7, 10, 13, …. Infinite Arithmetic 3, 7, 11, …, 51 Finite Arithmetic 1, 2, 4, …, 64 Finite Geometric 1, 2, 4, 8, … Infinite Geometric r>1 r < -1 Infinite Geometric -1 < r <1 No Sum

Find the sum, if possible:

Find the sum, if possible:

Find the sum, if possible:

Find the sum, if possible:

Find the sum, if possible:

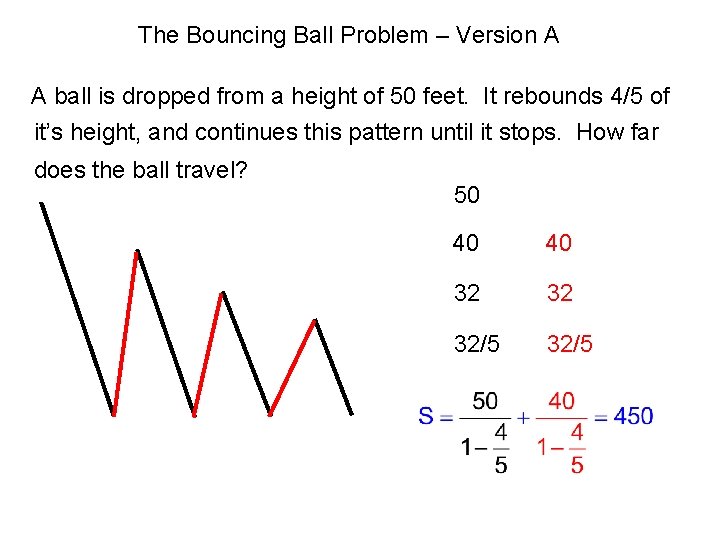
The Bouncing Ball Problem – Version A A ball is dropped from a height of 50 feet. It rebounds 4/5 of it’s height, and continues this pattern until it stops. How far does the ball travel? 50 40 40 32 32 32/5

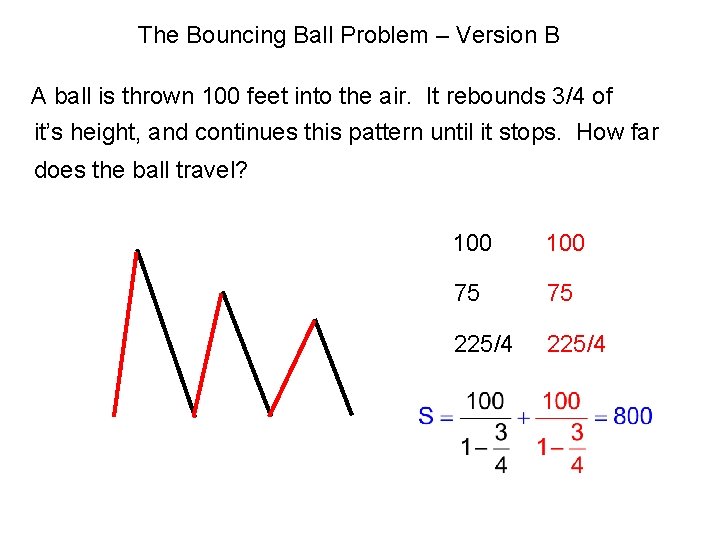
The Bouncing Ball Problem – Version B A ball is thrown 100 feet into the air. It rebounds 3/4 of it’s height, and continues this pattern until it stops. How far does the ball travel? 100 75 75 225/4

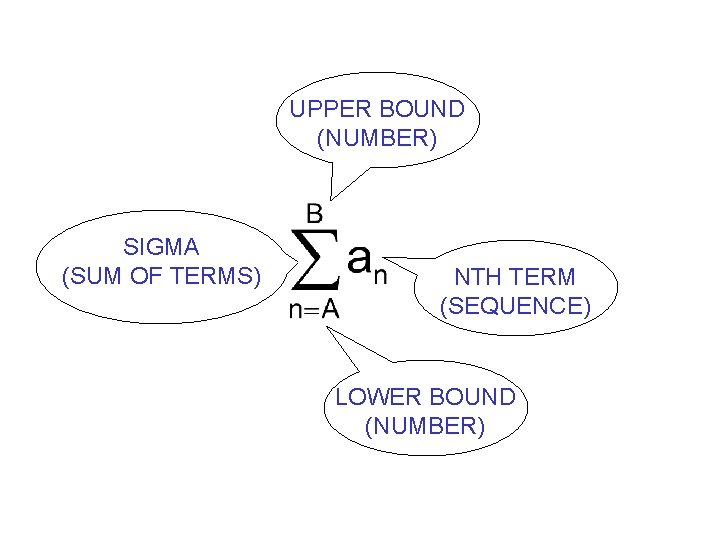
Sigma Notation

UPPER BOUND (NUMBER) SIGMA (SUM OF TERMS) NTH TERM (SEQUENCE) LOWER BOUND (NUMBER)
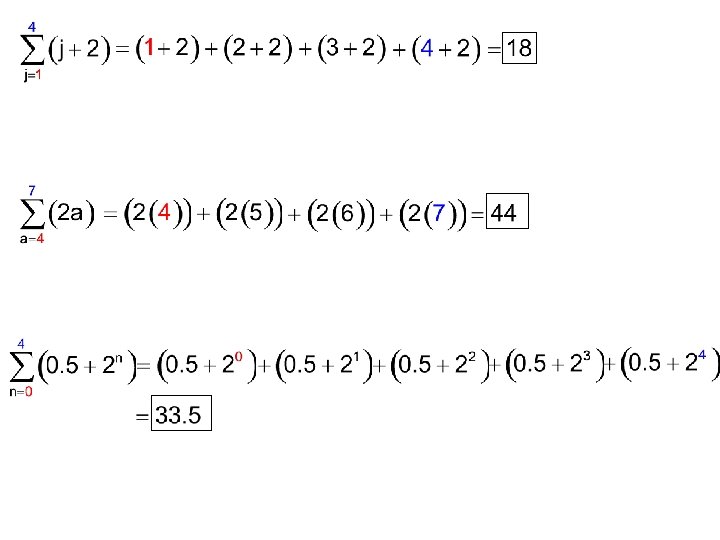
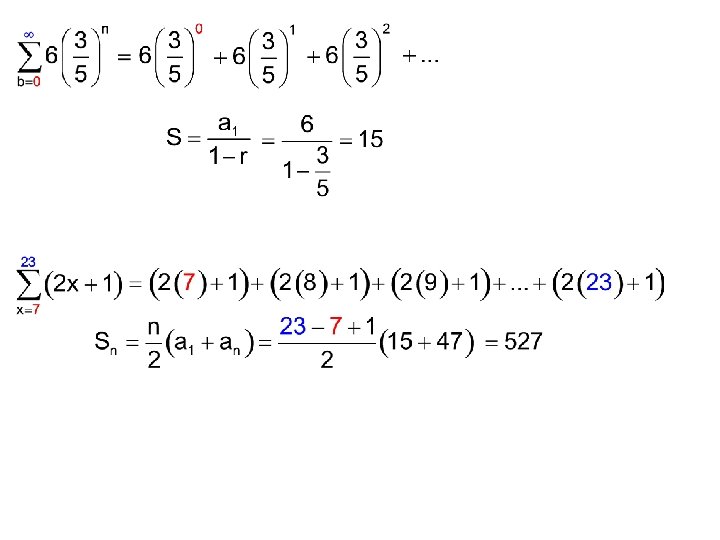


Rewrite using sigma notation: 3 + 6 + 9 + 12 Arithmetic, d= 3

Rewrite using sigma notation: 16 + 8 + 4 + 2 + 1 Geometric, r = ½

Rewrite using sigma notation: 19 + 18 + 16 + 12 + 4 Not Arithmetic, Not Geometric 19 + 18 + 16 + 12 + 4 -1 -2 -4 -8

Rewrite the following using sigma notation: Numerator is geometric, r = 3 Denominator is arithmetic d= 5 NUMERATOR: DENOMINATOR: SIGMA NOTATION:
 Arithmetic and geometric sequences and series
Arithmetic and geometric sequences and series 10-2 arithmetic sequences and series
10-2 arithmetic sequences and series 10-2 practice arithmetic sequences and series
10-2 practice arithmetic sequences and series Arithmetic sequences and series
Arithmetic sequences and series Sum of infinite arithmetic sequence
Sum of infinite arithmetic sequence Introduction to arithmetic sequences
Introduction to arithmetic sequences Arithmetic sequence sum formula
Arithmetic sequence sum formula Explicit formula
Explicit formula Geometric sequence formula
Geometric sequence formula Arithmetic and geometric sequences
Arithmetic and geometric sequences Geometric formula
Geometric formula Lesson 3: arithmetic and geometric sequences
Lesson 3: arithmetic and geometric sequences Geometric sequence formula
Geometric sequence formula Sum of geometric sequence
Sum of geometric sequence Arithmetic sequence
Arithmetic sequence Formula for geometric sequence
Formula for geometric sequence Write variable expressions for arithmetic sequences
Write variable expressions for arithmetic sequences Modeling with arithmetic sequences
Modeling with arithmetic sequences Recursive formula for arithmetic sequence
Recursive formula for arithmetic sequence Constructing arithmetic sequences
Constructing arithmetic sequences Find the nth term of the sequence 74, 67, 60, 53.
Find the nth term of the sequence 74, 67, 60, 53. Unit 10 sequences and series
Unit 10 sequences and series Chapter 12 sequences and series answers
Chapter 12 sequences and series answers 10-3 geometric sequences and series
10-3 geometric sequences and series Module 12 sequences and series answers
Module 12 sequences and series answers 10-3 practice geometric sequences and series
10-3 practice geometric sequences and series 10-1 sequences series and sigma notation
10-1 sequences series and sigma notation Sum of gp formula
Sum of gp formula Chapter 1 sequences and series
Chapter 1 sequences and series Chapter 1 sequences and series
Chapter 1 sequences and series Chapter 1 sequences and series
Chapter 1 sequences and series Sequence and series
Sequence and series Sequences and series math 20-1
Sequences and series math 20-1 Sequences and series games
Sequences and series games Sequences and series math 20-1
Sequences and series math 20-1 Recursive arithmetic formula
Recursive arithmetic formula Geometric sequence examples
Geometric sequence examples Rearranging formulae dr frost
Rearranging formulae dr frost Infinite series convergence
Infinite series convergence Difference between arithmetic series and sequence
Difference between arithmetic series and sequence Partial sum formula
Partial sum formula Differentiate finite sequence from an infinite sequence
Differentiate finite sequence from an infinite sequence Arithmetic sequence
Arithmetic sequence Arithmetic series formula
Arithmetic series formula Evaluating arithmetic series
Evaluating arithmetic series Geometric series formula
Geometric series formula S(n) formula
S(n) formula Lesson 4: arithmetic series
Lesson 4: arithmetic series Infinite arithmetic series
Infinite arithmetic series Series aiding and series opposing
Series aiding and series opposing Maclaurin series vs taylor series
Maclaurin series vs taylor series








































































