LESSON 10 1 Sequences Series and Sigma Notation























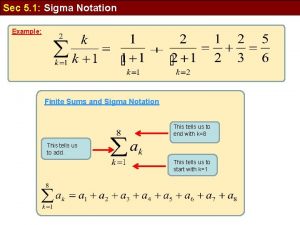
![Sums in Sigma Notation A. Find . = [(1)2 – 1] + [(2)2 – Sums in Sigma Notation A. Find . = [(1)2 – 1] + [(2)2 –](https://slidetodoc.com/presentation_image_h2/c1deec872a5fa03f24472909a4c754fe/image-33.jpg)


- Slides: 37

LESSON 10– 1 Sequences, Series, and Sigma Notation

Five-Minute Check (over Chapter 9) TEKS Then/Now New Vocabulary Example 1: Find Terms of Sequences Example 2: Recursively Defined Sequences Example 3: Real-World Example: Fibonacci Sequence Example 4: Convergent and Divergent Sequences Example 5: The nth Partial Sum Key Concept: Sigma Notation Example 6: Sums in Sigma Notation

Over Chapter 9 Find three different pairs of polar coordinates that name (– 3, A. B. C. D. ) if – 2π ≤ θ ≤ 2π.

Over Chapter 9 Determine the symmetry, zeros, and maximum r-values of r = 2 – 2 sin θ. Then use the information to graph the function. A. symmetric with respect to the line ; |r | = 4 when ; zeros for r when = ; C. symmetric with respect to the polar axis; |r | = 4 when = 0; zeros for r when = ; B. symmetric with respect to the line ; |r | = 4 when ; zeros for r when ; D. symmetric with respect to the polar axis; |r | = 4 when = 0; zeros for r when = ;

Over Chapter 9 Write r = A. x 2 = 4(y + 1) B. y 2 = 4(x + 1) C. x 2 = 4(y – 1) D. (x + 1) = y 2 in rectangular form.

Over Chapter 9 Which of the following represents 4 − 4 i in polar form? A. B. C. D.

Targeted TEKS P. 5(B) Represent arithmetic sequences and geometric sequences using recursive formulas. Mathematical Processes P. 1(A), P. 1(D)

You used functions to generate ordered pairs and used graphs to analyze end behavior. (Lesson 1 -1 and 1 -3) • Investigate several different types of sequences. • Use sigma notation to represent and calculate sums of series.

• sequence • diverge • term • series • finite sequence • finite series • infinite sequence • nth partial sum • recursive sequence • infinite series • explicit sequence • sigma notation • Fibonacci sequence • converge

Find Terms of Sequences A. Find the next four terms of the sequence 3, – 1, – 5, – 9, . . The nth term of this sequence is not given. One possible pattern is that each term is 4 less than the previous term. Therefore, a sample answer for the next four terms is 13, 17, 21, and 25. Answer: – 13, – 17, – 21, – 25

Find Terms of Sequences B. Find the next four terms of the sequence 18, 15, 10, 3, …. The nth term of this sequence is not given. If we subtract each term from the term that follows, we start to see a possible pattern. a 2 a 1 = 15 – 18 or – 3 a 3 a 2 = 10 – 15 = – 5 a 4 a 3 = 3 – 10 = – 7 It appears that each term is generated by subtracting the next successive odd number. Therefore, a sample answer for the next four terms is 6, – 17, – 30, and – 45. Answer: – 6, – 17, – 30, – 45

Find Terms of Sequences C. Find the first four terms of the sequence given by an = n 3 + 1. Use the explicit formula to find an for n = 1, 2, 3, and 4. a 1 = 13 + 1 or 2 n = 1 a 3 = 33 + 1 or 28 n=3 a 2 = 23 + 1 or 9 n = 2 a 4 = 43 + 1 or 65 n=4 The first four terms in the sequence are 2, 9, 28, and 65. Answer: 2, 9, 28, 65

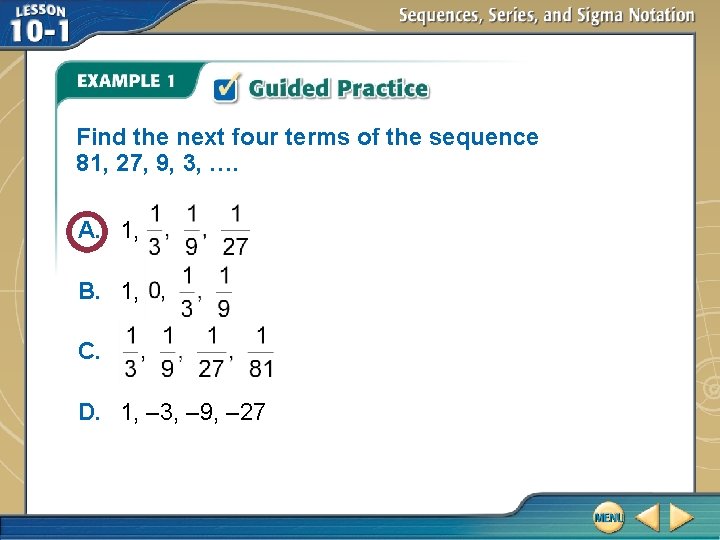
Find the next four terms of the sequence 81, 27, 9, 3, …. A. 1, B. 1, C. D. 1, – 3, – 9, – 27

Recursively Defined Sequences Find the fourth term of the recursively defined sequence a 1 = 3, an = 3 an – 1 n + 2, where n 2. Since the sequence is defined recursively, all the terms before the fourth term must be found first. Use the given first term, a 1 = 3, and the recursive formula for an. a 2 = 3 a 2 – 1 – 2 + 2 n=2 = 3 a 1 Simplify. = 3(3) or 9 a 1 = 3 a 3 = 3 a 3 – 1 – 3 + 2 = 3 a 2 – 1 or 26 n=3 a 2 = 9

Recursively Defined Sequences a 4 = 3 a 4 – 1 – 4 + 2 = 3 a 3 – 2 or 76 The fourth term is 76. Answer: 76 n=4 a 4 = 76

Find the fifth term of the recursively defined sequence a 1 = 28, an = A. B. C. D. an – 1 + 4, where n 2.

Fibonacci Sequence NATURE Suppose that a stem has to grow for two months before it is strong enough to support branches. At the end of the second month, it sprouts a new branch and continues to sprout one new branch each month. The new branches grow similarly. How many branches will a plant have after 18 months if no branches are removed? During the first two months, there will only be one branch, the stem. At the end of the second month, the stem will produce a new branch, making the total for the third month two branches. The new branch will grow and develop two months before producing a new branch of its own, but the original branch will now produce a new branch each month.

Fibonacci Sequence The table below shows the pattern. Each term is the sum of the previous two terms. This pattern can be written as the recursive formula a 1 = 1, a 2 = 1, an = an – 2 + an – 1 , where n ≥ 3. Therefore, to find the number of branches after 18 months, continue the table until you find the number of branches after 16 months and 17 months.

Fibonacci Sequence The number of branches are shown in the table below. If no branches are removed, a plant will have 2584 branches after 18 months. Answer: 2584 branches

NATURE Suppose that a stem has to grow for two months before it is strong enough to support branches. At the end of the second month, it sprouts a new branch and continues to sprout one new branch each month. The new branches grow similarly. How many branches will a plant have after 20 months if no branches are removed? A. 1597 B. 2584 C. 4181 D. 6765

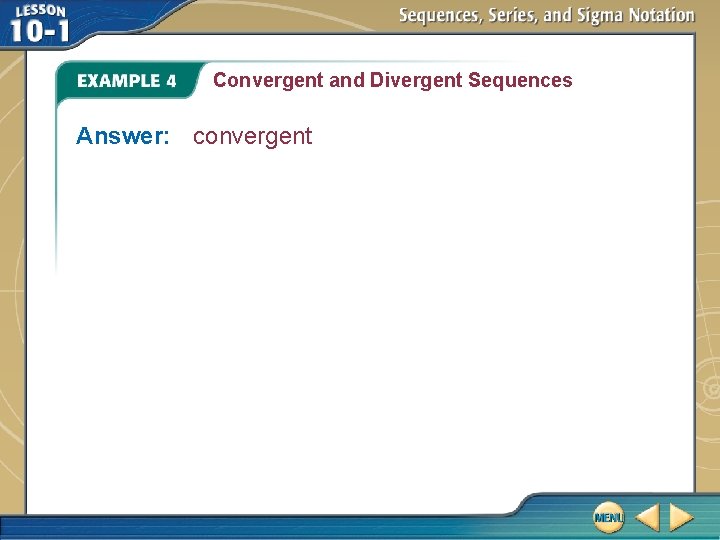
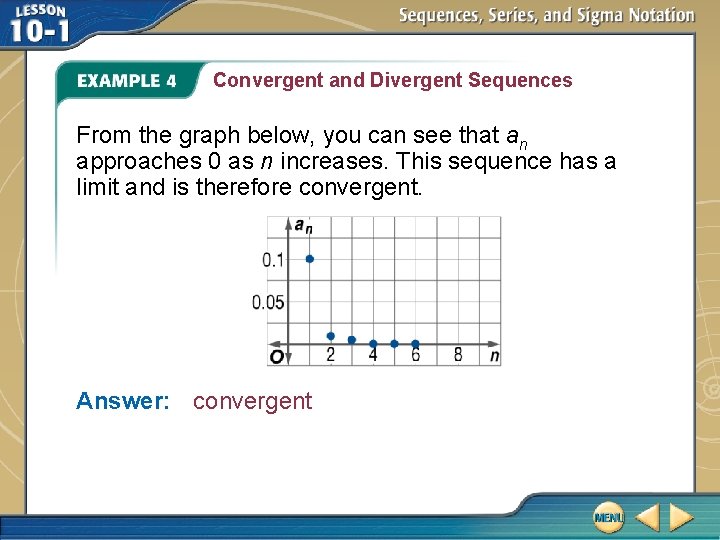
Convergent and Divergent Sequences A. Determine if the sequence is convergent or divergent. The first eight terms of this sequence are given or approximated below. a 1 = 1000 a 2 = 250 a 3 = 62. 5 a 4 = 15. 625 a 5 = 3. 90625 a 6 = 0. 97656 a 7 = 0. 24414 a 8 = 0. 06104 From the graph at the right, you can see that an approaches 0 as n increases. This sequence has a limit and is therefore convergent.

Convergent and Divergent Sequences Answer: convergent

Convergent and Divergent Sequences B. Determine if the sequence is convergent or divergent. The first eight terms of this sequence are – 1, 2, – 4, 8, – 16, 32, – 64, and 128. From the graph below, you can see that an does not approach a finite number. Therefore, this sequence is divergent.

Convergent and Divergent Sequences Answer: divergent

Convergent and Divergent Sequences C. Determine if the sequence is convergent or divergent. The first eight terms of this sequence are given or approximated below. a 1 = 0. 1 a 2 = 0. 00667 a 3 = 0. 0006 a 4 =0. 000057 a 5 = 0. 0000056 a 6 = 0. 00000055 a 7 = 0. 000000054 a 8 = 0. 000053

Convergent and Divergent Sequences From the graph below, you can see that an approaches 0 as n increases. This sequence has a limit and is therefore convergent. Answer: convergent

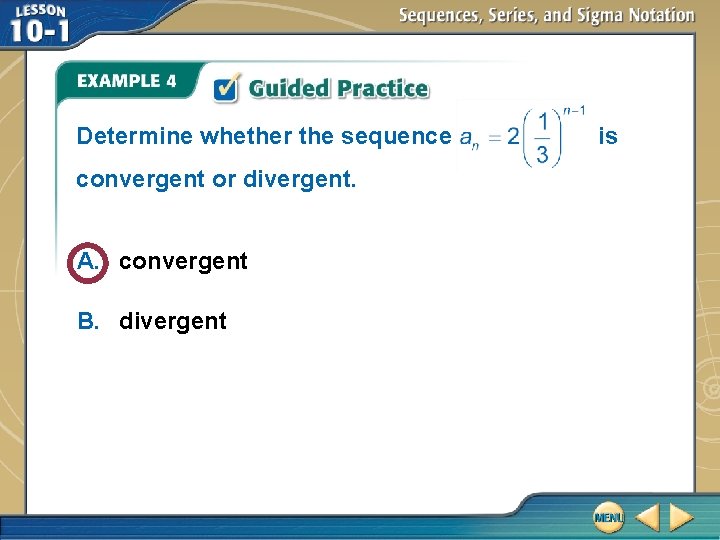
Determine whether the sequence convergent or divergent. A. convergent B. divergent is

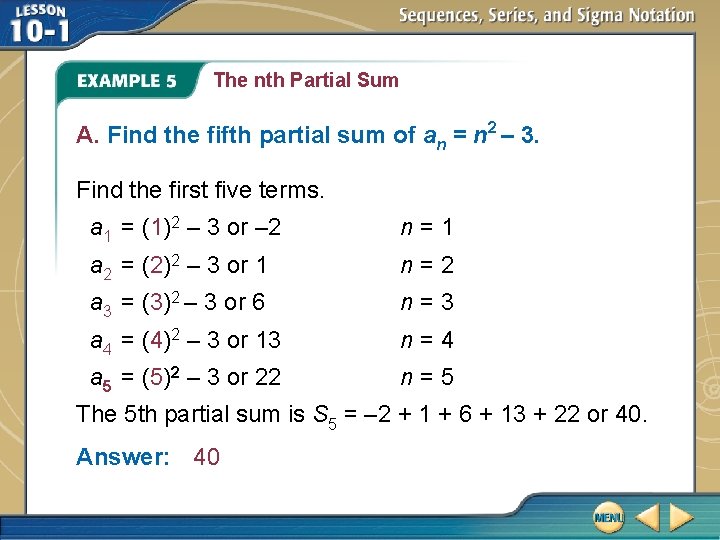
The nth Partial Sum A. Find the fifth partial sum of an = n 2 – 3. Find the first five terms. a 1 = (1)2 – 3 or – 2 n=1 a 2 = (2)2 – 3 or 1 n=2 a 3 = (3)2 – 3 or 6 n=3 a 4 = (4)2 – 3 or 13 n=4 a 5 = (5)2 – 3 or 22 n=5 The 5 th partial sum is S 5 = – 2 + 1 + 6 + 13 + 22 or 40. Answer: 40

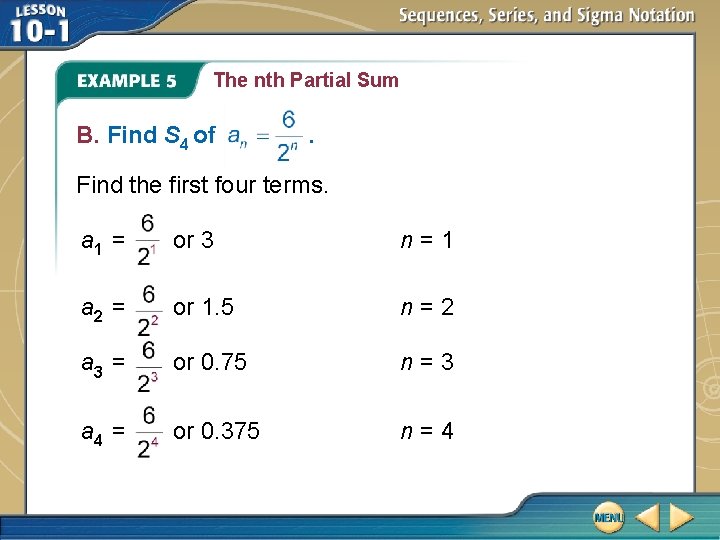
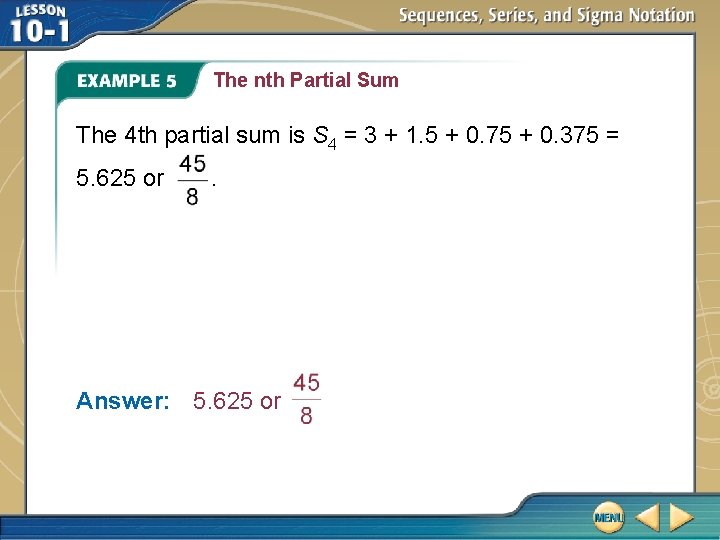
The nth Partial Sum B. Find S 4 of . Find the first four terms. a 1 = or 3 n=1 a 2 = or 1. 5 n=2 a 3 = or 0. 75 n=3 a 4 = or 0. 375 n=4

The nth Partial Sum The 4 th partial sum is S 4 = 3 + 1. 5 + 0. 75 + 0. 375 = 5. 625 or . Answer: 5. 625 or

Find the fifth partial sum of an = (– 3)n – 2. A. – 246 B. – 193 C. 365 D. 534

![Sums in Sigma Notation A Find 12 1 22 Sums in Sigma Notation A. Find . = [(1)2 – 1] + [(2)2 –](https://slidetodoc.com/presentation_image_h2/c1deec872a5fa03f24472909a4c754fe/image-33.jpg)
Sums in Sigma Notation A. Find . = [(1)2 – 1] + [(2)2 – 2] + [(3)2 – 3] + [(4)2 – 4] = 0 + 2 + 6 + 12 = 20 Answer: 20

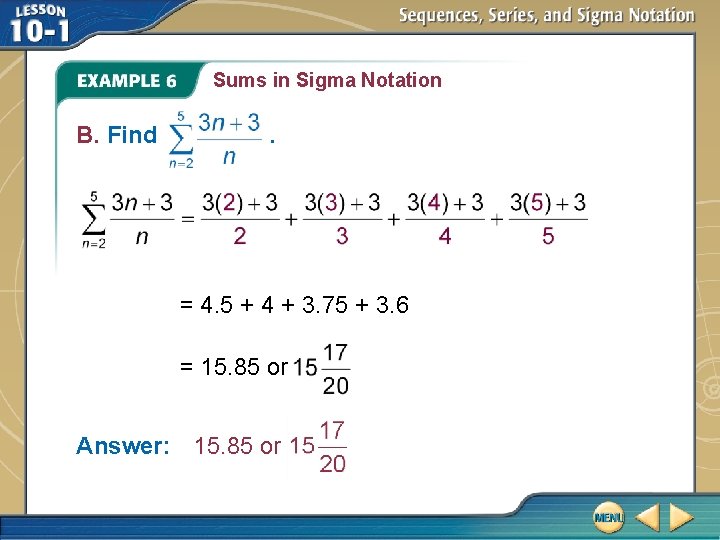
Sums in Sigma Notation B. Find . = 4. 5 + 4 + 3. 75 + 3. 6 = 15. 85 or Answer: 15. 85 or

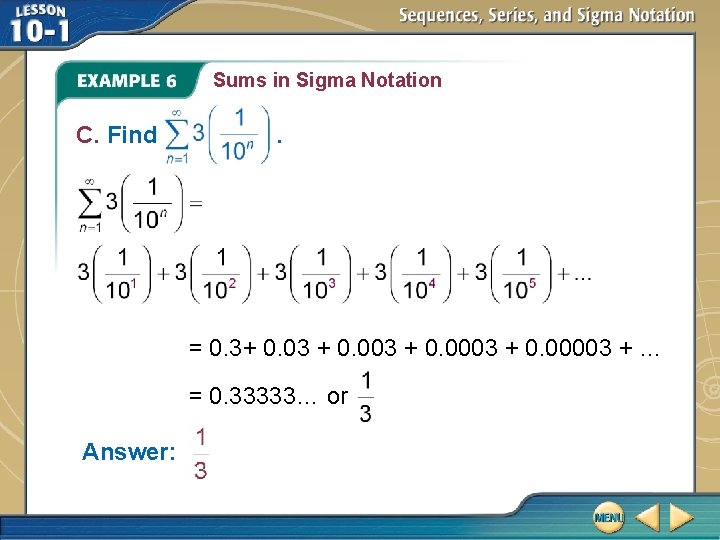
Sums in Sigma Notation C. Find . = 0. 3+ 0. 03 + 0. 0003 + 0. 00003 + … = 0. 33333… or Answer:

Find A. 92 B. 123 C. 215 D. 429 .

LESSON 10– 1 Sequences, Series, and Sigma Notation
 10-1 sequences series and sigma notation
10-1 sequences series and sigma notation Arithmetic sigma notation
Arithmetic sigma notation Sigma notation diagram
Sigma notation diagram Arithmetic and geometric sequences and series
Arithmetic and geometric sequences and series Unit 10 sequences and series homework 1 answers
Unit 10 sequences and series homework 1 answers Unit 10 sequences and series homework 1 answers
Unit 10 sequences and series homework 1 answers Chapter 12 sequences and series answers
Chapter 12 sequences and series answers 10-3 geometric sequences and series
10-3 geometric sequences and series Module 12 sequences and series answers
Module 12 sequences and series answers Recursive formula geometric
Recursive formula geometric 10-2 arithmetic sequences and series answer key
10-2 arithmetic sequences and series answer key 10-3 geometric sequences and series
10-3 geometric sequences and series Series math
Series math Chapter 1 sequences and series
Chapter 1 sequences and series Chapter 1 sequences and series
Chapter 1 sequences and series Sequences and series math 20-1
Sequences and series math 20-1 Pre calc sequences and series
Pre calc sequences and series Math 20-1 sequences and series
Math 20-1 sequences and series Sequences and series games
Sequences and series games Arithmetic
Arithmetic Sequences and series math 20-1
Sequences and series math 20-1 Sequences and series
Sequences and series Geometric sequence example
Geometric sequence example Dr frost sequences
Dr frost sequences 9 + 1 = 10
9 + 1 = 10 Discrete mathematics
Discrete mathematics Vcom white coat ceremony
Vcom white coat ceremony Sigma sigma phi vcom
Sigma sigma phi vcom Lesson 3: arithmetic and geometric sequences
Lesson 3: arithmetic and geometric sequences Pico engineering notation
Pico engineering notation Reverse polish notation
Reverse polish notation Polish notation examples
Polish notation examples Definite integrals as a limit of a sum
Definite integrals as a limit of a sum What is sigma notation
What is sigma notation Consider the infinite geometric series
Consider the infinite geometric series Summation math
Summation math Formula sigma
Formula sigma Differentiate finite from infinite sequence
Differentiate finite from infinite sequence