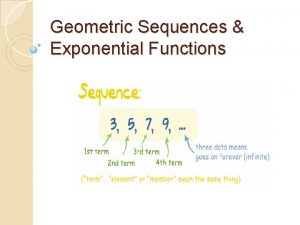
LESSON 10 3 Geometric Sequences and Series FiveMinute

LESSON 10– 3 Geometric Sequences and Series

Five-Minute Check (over Lesson 10 -2) TEKS Then/Now New Vocabulary Example 1: Geometric Sequences Key Concept: The nth Term of a Geometric Sequence Example 2: Explicit and Recursive Formulas Example 3: nth Terms Example 4: Real-World Example: nth Term of a Geometric Sequence Example 5: Geometric Means Key Concept: Sum of a Finite Geometric Series Example 6: Sums of Geometric Series Example 7: Geometric Sum in Sigma Notation Key Concept: The Sum of an Infinite Geometric Series Example 8: Real-World Example: Sums of Infinite Geometric Series

Over Lesson 10 -2 Determine the common difference and find the next four terms of the arithmetic sequence 5, – 1, – 7, – 13, …. A. d = – 6; – 19, – 25, – 31, – 37 B. d = – 5; – 18, – 23, – 28, – 33 C. d = – 5; – 19, – 25, – 31, – 37 D. d = 6; – 19, – 25, – 31, – 37

Over Lesson 10 -2 Write an explicit formula and a recursive formula for finding the nth term of the arithmetic sequence 2, 7, 12, 17, …. A. an = 5 n – 3; a 1 = 2, an = an – 1 + 5 B. an = 5 n; a 1 = 2, an = an – 1 + 5 C. an = 5 n + 2; a 1 = 7, an = an – 1 + 5 D. an = 7 n – 2; a 1 = 7, an = an – 1 + 5

Over Lesson 10 -2 Find a 1 for the arithmetic sequence for which a 25 = 42 and d = – 2. A. a 1 = 92 B. a 1 = 90 C. a 1 = 88 D. a 1 = – 8

Over Lesson 10 -2 Find n for the arithmetic sequence for which an = 127, a 1 = 83, and d = 4. A. n = 10 B. n = 11 C. n = 12 D. n = 13

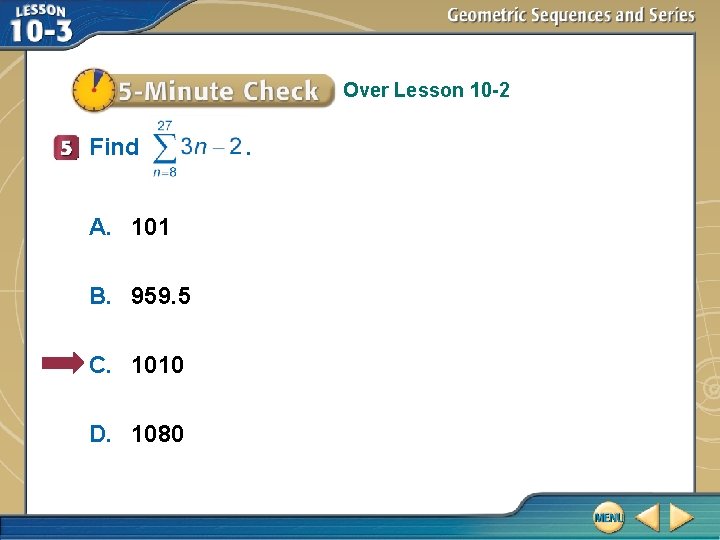
Over Lesson 10 -2 Find A. 101 B. 959. 5 C. 1010 D. 1080 .

Targeted TEKS P. 5(A) Evaluate finite sums and geometric series, when possible, written in sigma notation. P. 5(E) Calculate the n th term of a geometric series, the n th partial sum of a geometric series, and sum of an infinite geometric series when it exists. Also addresses P. 5(B) and P. 5(D). Mathematical Processes P. 1(D), P. 1(E)

You found terms and means of arithmetic sequences and sums of arithmetic series. (Lesson 10 -2) • Find nth terms and geometric means of geometric sequences. • Find sums of n terms of geometric series and sums of infinite geometric series.

• geometric sequence • common ratio • geometric means • geometric series

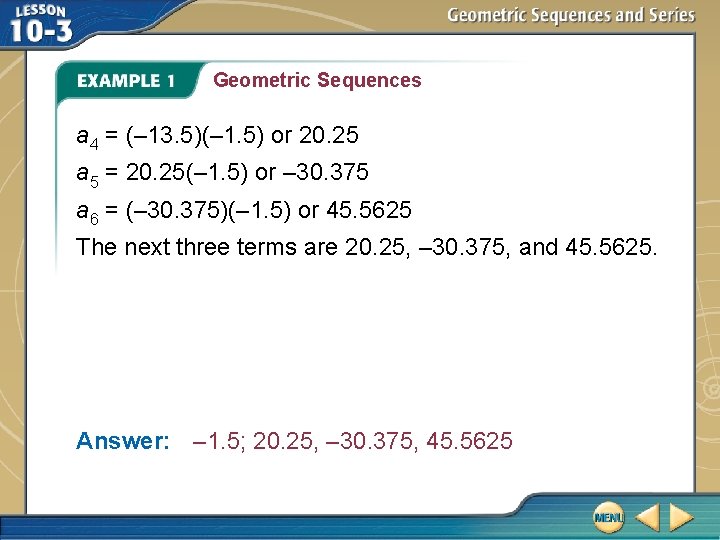
Geometric Sequences A. Determine the common ratio and find the next three terms of the geometric sequence – 6, 9, – 13. 5, …. First, find the common ratio. a 2 ÷ a 1 = 9 ÷ (– 6) or – 1. 5 Find the ratio between two pairs of consecutive terms to determine the common ratio. a 3 ÷ a 2 = – 13. 5 ÷ 9 or – 1. 5 The common ratio is – 1. 5. Multiply the third term by – 1. 5 to find the fourth term, and so on.

Geometric Sequences a 4 = (– 13. 5)(– 1. 5) or 20. 25 a 5 = 20. 25(– 1. 5) or – 30. 375 a 6 = (– 30. 375)(– 1. 5) or 45. 5625 The next three terms are 20. 25, – 30. 375, and 45. 5625. Answer: – 1. 5; 20. 25, – 30. 375, 45. 5625

Geometric Sequences B. Determine the common ratio and find the next three terms of the geometric sequence 243 n – 729, – 81 n + 243, 27 n – 81, …. First, find the common ratio. a 2 = – 81 n + 243 a 1 = 243 n – 729 Factor. Simplify.

Geometric Sequences a 3 = 27 n – 81 a 2 = – 81 n + 243 Factor. Simplify. The common ratio is . Multiply the third term by to find the fourth term, and so on.

Geometric Sequences The next three terms are – 9 n + 27, 3 n – 9, and –n + 3. Answer: ; – 9 n + 27, 3 n – 9, –n + 3

Determine the common ratio and find the next three terms of the geometric sequence 24, 84, 294, …. A. – 3; – 882, 2646, – 7938 B. 3. 5; 297. 5, 301, 304. 5 C. 3. 5; 1029, 3601. 5, 12, 605. 25 D. 60; 354, 414, 474

Explicit and Recursive Formulas Write an explicit formula and a recursive formula for finding the nth term in the sequence – 1, 2, – 4, …. First, find a common ratio. a 2 ÷ a 1 = 2 ÷ (– 1) or – 2 a 3 ÷ a 2 = – 4 ÷ 2 or – 2 The common ratio is – 2. Find the ratio between two pairs of consecutive terms to determine the common ratio.

Explicit and Recursive Formulas For an explicit formula, substitute a 1 = – 1 and r = – 2 in the nth term formula. an = a 1 r n – 1 nth term formula an = – 1(– 2)n – 1 a 1 = – 1 and r = – 2 The explicit formula is an = – 1(– 2) n – 1. For a recursive formula, state the first term a 1. Then indicate that the next term is the product of the previous term a n – 1 and r. a 1 = – 1; an = (– 2) an – 1 The recursive formula is a 1 = – 1; an = (– 2) an – 1. Answer: an = – 1(– 2)n – 1; a 1 = – 1; an = (– 2) an – 1

Find both an explicit formula and a recursive formula for the nth term of the geometric sequence 3, 16. 5, 90. 75, …. A. an = 3(5. 5)n – 1; a 1 = 3, an = 5. 5 an – 1 B. an = 5. 5(3)n – 1; a 1 = 3, an = 5. 5 an – 1 C. an = 3(5. 5)n – 1; a 1 = 3, an = 5 an – 1 D. an = – 2. 5 + 5. 5 n ; a 1 = 3, an = 5. 5 an – 1

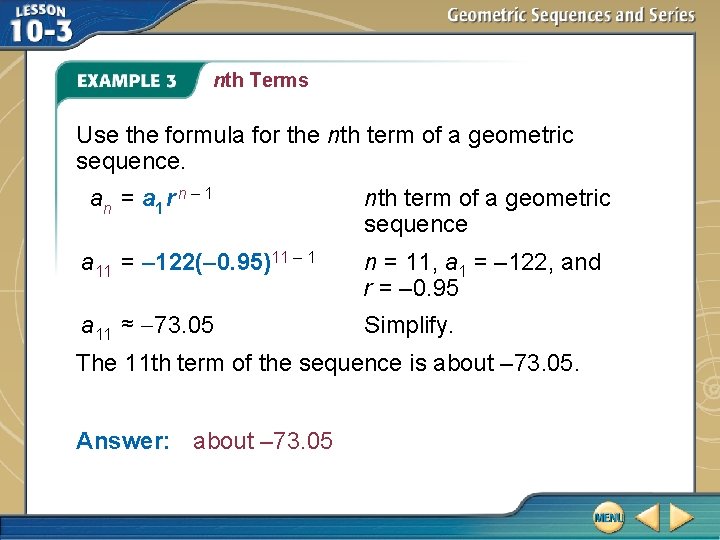
nth Terms Find the 11 th term of the geometric sequence – 122, 115. 9, – 110. 105, …. First, find the common ratio. a 2 ÷ a 1 = 115. 9 ÷ (– 122) or – 0. 95 a 3 ÷ a 2 = – 110. 105 ÷ 115. 9 or – 0. 95 Find the ratio between two pairs of consecutive terms to determine the common ratio.

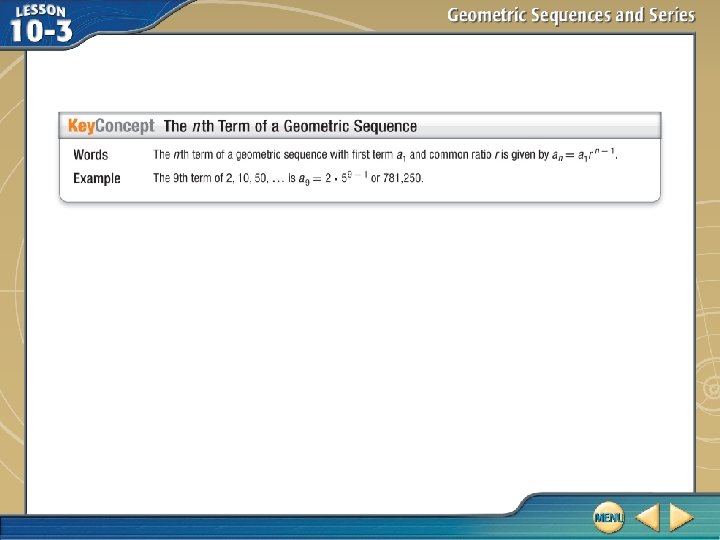
nth Terms Use the formula for the nth term of a geometric sequence. an = a 1 r n – 1 nth term of a geometric sequence a 11 = – 122(– 0. 95)11 – 1 n = 11, a 1 = – 122, and r = – 0. 95 a 11 ≈ 73. 05 Simplify. The 11 th term of the sequence is about – 73. 05. Answer: about – 73. 05

Find the 25 th term of the geometric sequence 324, 291. 6, 262. 44, …. A. about 20. 93 B. about 23. 26 C. about 25. 84 D. about 28. 72

nth Term of a Geometric Sequence A. REAL ESTATE A couple purchased a home for $225, 000. At the end of each year, the value of the home appreciates 3%. Write an explicit formula for finding the value of the home after n years. If the house’s value appreciates at a rate of 3% per year, it will have a value of 100% + 3% or 103% of its original value. Note that the original value given represents the a 0 and not the a 1 term, so we need to use an adjusted formula for the nth term of this geometric sequence.

nth Term of a Geometric Sequence first term a 1 = a 0 r second term a 2 = a 0 r 2 nth term a n = a 0 r n Use this adjusted formula to find an explicit formula for the value of the house after n years. an = a 0 r n Adjusted nth term of a geometric sequence an = 225, 000(1. 03)n a 0 = 225, 000, r = 1. 03

nth Term of a Geometric Sequence An explicit formula for the value of the home after n years is an = 225, 000(1. 03)n. Answer: an = 225, 000(1. 03)n

nth Term of a Geometric Sequence B. REAL ESTATE A couple purchased a home for $225, 000. At the end of each year, the value of the home appreciates 3%. What is the value of the home after the tenth year? Evaluate the formula you found in part A with n = 10. an = 225, 000(1. 03)n Original formula = 225, 000(1. 03)10 n = 10 ≈ 302, 381. 19 Simplify.

nth Term of a Geometric Sequence The value of the home after the tenth year is about $302, 381. 19. The value of the home at each year is shown as a point on the graph. The function connecting the points represents exponential growth. Answer: about $302, 381. 19

A. BOAT Jeremy purchased a boat for $12, 500. By the end of each year, the value of the boat depreciates 4%. Write an explicit formula for finding the value of the boat after n years. A. an = 12, 500(1. 04)n B. an = 12, 500(0. 96)n C. an = 12, 500(0. 96)n – 1 D. an = 12, 000(0. 96)n

B. BOAT Jeremy purchased a boat for $12, 500. At the end of each year, the value of the boat depreciates 4%. What is the value of the boat after 12 years? A. $20, 012. 90 B. $7658. 87 C. $7977. 99 D. $7352. 52

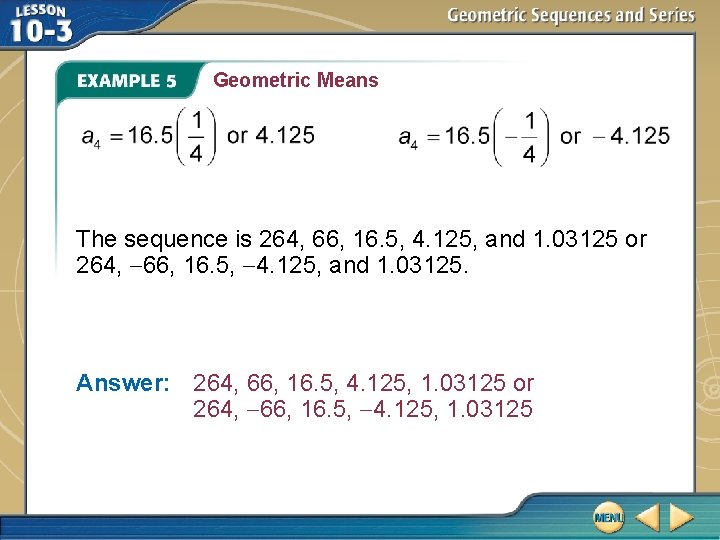
Geometric Means Write a sequence that has three geometric means between 264 and 1. 03125. ? ? The sequence will resemble 264, _____, 1. 03125. ? Note that a 1 = 264, n = 5, and a 5 = 1. 03125. Find the common ratio using the nth term for a geometric sequence formula. a 5 = a 1 r n – 1 1. 03125 = 264 r 5 – 1 nth term of a geometric sequence a 5 = 1. 03125, a 1 = 264, and n = 5

Geometric Means ± = r 4 Simplify and divide each side by 264. =r Take the fourth root of each side. The common ratio is ± means. . Use r to find the geometric

Geometric Means The sequence is 264, 66, 16. 5, 4. 125, and 1. 03125 or 264, 66, 16. 5, 4. 125, and 1. 03125. Answer: 264, 66, 16. 5, 4. 125, 1. 03125 or 264, 66, 16. 5, 4. 125, 1. 03125

Write a geometric sequence that has two geometric means between 20 and 8. 4375. A. 20, 15, 11. 25, 8. 4375 B. 20, 16. 15, 12. 296, 8. 4375 C. 20, 14. 2188, 8. 4375 D. 15, 11. 25

Sums of Geometric Series A. Find the sum of the first eleven terms of the geometric series 4, – 6, 9, …. First, find the common ratio. a 2 ÷ a 1 = – 6 ÷ 4 or – 1. 5 Find the ratio between two pairs of consecutive terms to determine the common ratio. a 3 ÷ a 2 = 9 ÷ (– 6) or – 1. 5 The common ratio is – 1. 5. Use Formula 1 to find the sum of the series.

Sums of Geometric Series Sum of a geometric series formula 1. n = 11, a 1 = 4, and r = – 1. 5 Simplify. The sum of the geometric series is about 140. Answer: about 140

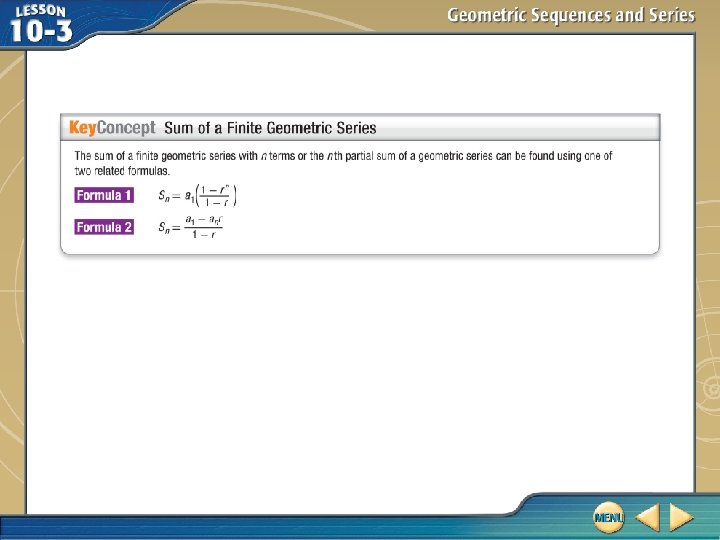
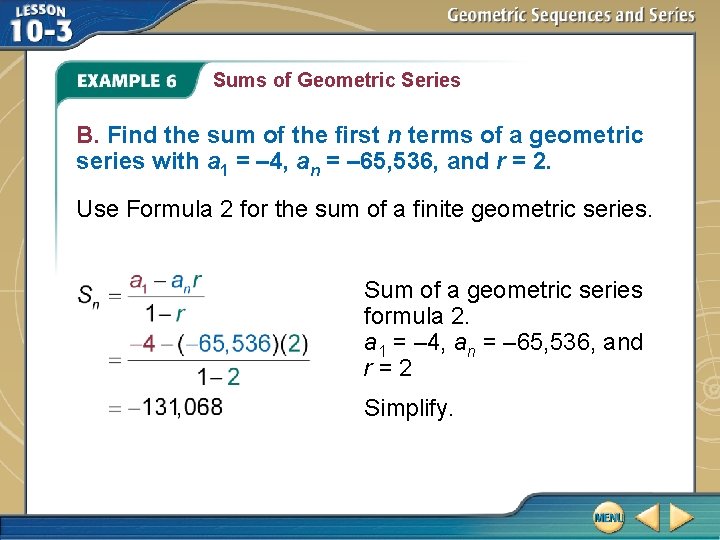
Sums of Geometric Series B. Find the sum of the first n terms of a geometric series with a 1 = – 4, an = – 65, 536, and r = 2. Use Formula 2 for the sum of a finite geometric series. Sum of a geometric series formula 2. a 1 = – 4, an = – 65, 536, and r=2 Simplify.

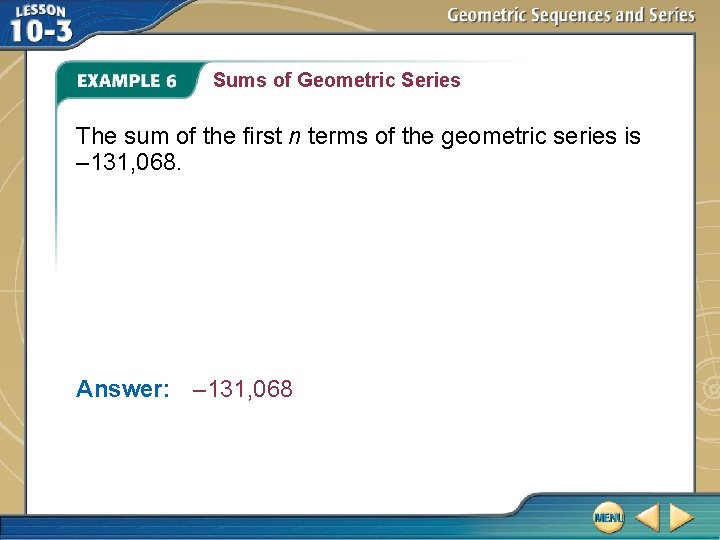
Sums of Geometric Series The sum of the first n terms of the geometric series is – 131, 068. Answer: – 131, 068

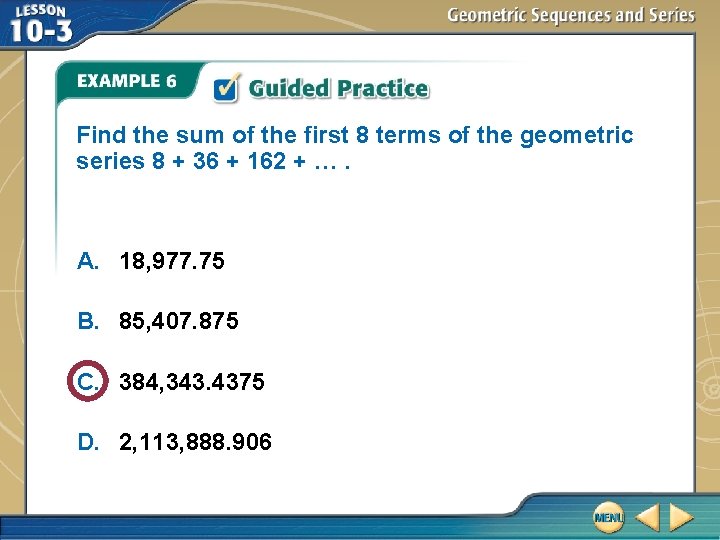
Find the sum of the first 8 terms of the geometric series 8 + 36 + 162 + …. A. 18, 977. 75 B. 85, 407. 875 C. 384, 343. 4375 D. 2, 113, 888. 906

Geometric Sum in Sigma Notation Find Method 1 . Use Formula 1. Find n, a 1, and r. n = 8 – 3 + 1 or 6 Upper bound minus lower bound plus 1 a 1 = – 2(– 2)3– 1 or – 8 n=3 r = – 2 r is the base of the exponential function. Substitute n = 6, a 1 = 8, and r = 2 into Formula 1.

Geometric Sum in Sigma Notation Formula 1 n = 6, a 1 = – 8, and r = – 2 Simplify. Method 2 Use Formula 2. Find an. a n = a 1 r n 1 nth term of a geometric sequence

Geometric Sum in Sigma Notation = – 8(– 2)6– 1 a 1 = 8, r = 2, and n = 6 = 256 Simplify. Substitute a 1 = 8, an = 256, and r = 2 into Formula 2 n = 6, a 1 = 8, an = 256, and r = 2 Simplify. Therefore, Answer: 168 = 168.

Find A. 10, 912 B. 32, 768 C. 43, 680 D. 174, 752 .

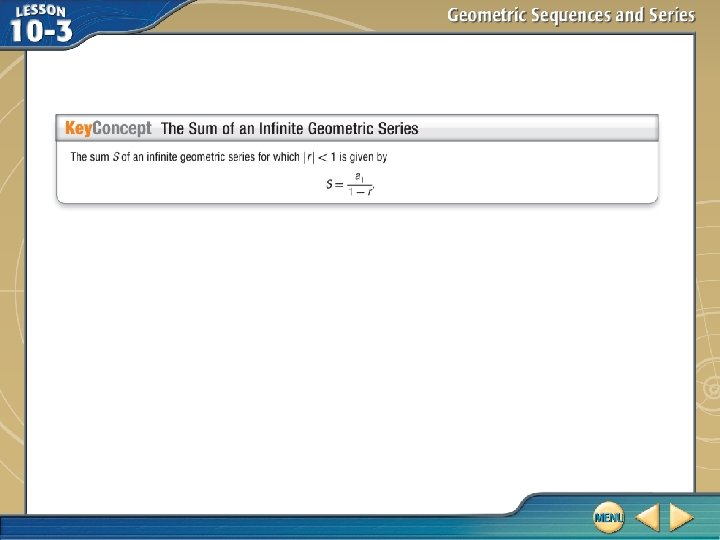
Sums of Infinite Geometric Series A. If possible, find the sum of the infinite geometric series 24 + 18 + 13. 5 + …. First, find the common ratio. a 2 ÷ a 1 = 18 ÷ 24 or . Find the ratio between two pairs of consecutive terms to determine the common ratio. a 3 ÷ a 2 = 13. 5 ÷ 18 or The common ratio r is , and . This infinite geometric series has a sum. Use the formula for the sum of an infinite geometric series.

Sums of Infinite Geometric Series Sum of an infinite geometric series formula a 1 = 9 and r = Simplify. The sum of the infinite series is 96. Answer: 96

Sums of Infinite Geometric Series B. If possible, find the sum of the infinite geometric series 0. 33 + 0. 66 + 1. 32 + …. First, find the common ratio. a 2 ÷ a 1 = 0. 66 ÷ 0. 33 or 2 Find the ratio between two pairs of consecutive terms to determine the common ratio. a 3 ÷ a 2 = 1. 32 ÷ 0. 66 or 2 The common ratio r is 2, and |2| > 1. Therefore, this infinite geometric series has no sum. Answer: does not exist

Sums of Infinite Geometric Series C. If possible, find . The common ratio r is 0. 65, and |0. 65| < 1. Therefore, this infinite geometric series has a sum. Find a 1 = 3(0. 65)2 – 1 Lower bound = 2 = 1. 95 Use the formula for the sum of an infinite geometric series to find the sum.

Sums of Infinite Geometric Series Sum of an infinite geometric series formula a 1 = 1. 95 and r = 0. 65 Simplify. Answer:

If possible, find the sum of the infinite geometric series . A. 1. 5 B. 7. 5 C. 30 D. does not exist

LESSON 10– 3 Geometric Sequences and Series