Relations are Not Sets of Ordered Pairs Ingvar

Relations are Not Sets of Ordered Pairs Ingvar Johansson, Institute for Formal Ontology and Medical Information Science, Saarbrücken 2004 -10 -09

The Importance of Relations • The question of relations is one of the most important that arise in philosophy, as most other issues turn on it: monism and pluralism; the question whether anything is wholly true except the whole of truth, or wholly real except the whole of reality; idealism and realism, in some of their forms; perhaps the very existence of philosophy as a subject distinct from science and possessing a method of its own. (Bertrand Russell, Logical Atomism, 1924. )

General Message • Features of representations must not be conflated with what is represented.

Specific Message • An internal relation can be represented by, but not be identical with an ordered pair or a set of ordered pairs.

Interesting Consequence • There are no anti-symmetrical internal relations in the language-independent world.

Identity and Representation • Circles are not identical with an equation. • Relations are not identical with sets of ordered pairs, • In both cases, it is merely a matter of representation. (x - a)2 + (y - b)2 = r 2 y b a x

Relations in Set Theory • relation, a two-or-more-place property (e. g. loves or between), or the extension of such a property. In set theory, a relation is any set of ordered pairs (or triples, etc. , but these are reducible to pairs). For simplicity, the formal exposition here uses the language of set theory, although an intensional (property -theoretic) view is later assumed. (The Cambridge Dictionary of Philosophy, 1999. )

Quotation • “Because relations are sets of ordered pairs, we can combine them using set of operations of union, intersection, and complement. These are called Boolean operations. ”

Relation Terminology • • • Relation – relations Relatum – relata Binary, ternary, …, n-ary Symbolism: Rab (=a. Rb), Rabcd, etc. Ordered pair: <a, b> Set of ordered pairs: <x, y>: such that … or <a, b>, <f, g>, . . .

Kinds of Ontological Relations • Relations of Existential dependence; relata are existentially dependent on each other, e. g. , perceived color and perceived spatial extension. • Intentional relations; can exist with only one relatum, e. g. , love. • External relations; independent of the qualities of the relata related, e. g. spatial distance. • Internal relations (comparative, grounded); dependent on the qualities of the relata related, e. g. larger than, lighter than, rounder than.

Internal Relations Between Quality Instances are Grounded in Universals T 1 : a T 2: b • The thing T 1 is larger than the thing T 2 because T 1 has an area-instance, a, that is larger than the area-instance of T 2, b. • Every area-instance that instantiates the same universal as a is larger than every area-instance that instantiates the same universal as b.

Internal Relations have Specific Features a b • Possibly, a exists but not b, or vice versa (compare existential dependence). • Necessarily: if both a and b exist, then the relation of “being larger than” is instantiated (compare external relations).

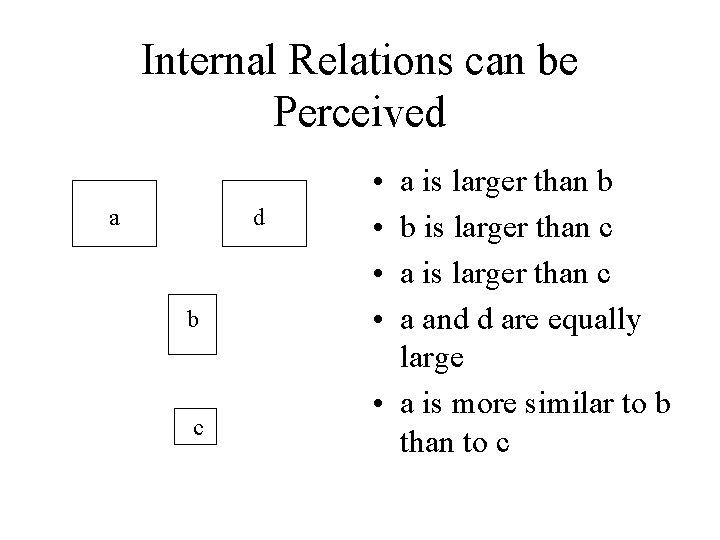
Internal Relations can be Perceived a d b c • • a is larger than b b is larger than c a and d are equally large • a is more similar to b than to c

Internal Relations require a Determinable a d b c • a is larger than b • a and d are equally large • a is more similar to b than to c • a, b, c, and d are different determinate instances of the same determinable.

Internal Relations require a Determinable • Statements describing internal relations: “a is smaller than b”, “a is heavier than b”, “a is more electrically charged than b”, “a has greater intensity than b”, etc. • These internal relations have different relata of the same kind. • Resemblance (both exact and non-exact) is always resemblance in a certain respect. • A determinate-determinable distinction (W. E. Johnson) has to be made explicit.

Exact Resemblance • When two things are equally large there is a relation of exact resemblance between the two quality instances in question. • But there is only one universal. • When two particulars are qualitatively identical there is necessarily a relation of exact resemblance between them.

Non-Exact Resemblance • When two things have different areas there is a relation of non-exact resemblance between the two area instances in question. • There are then two universals. • Between these universals there is an internal relation, a determinate kind of resemblance. • When the universals are instantiated there is also an internal relation between the corresponding instances.

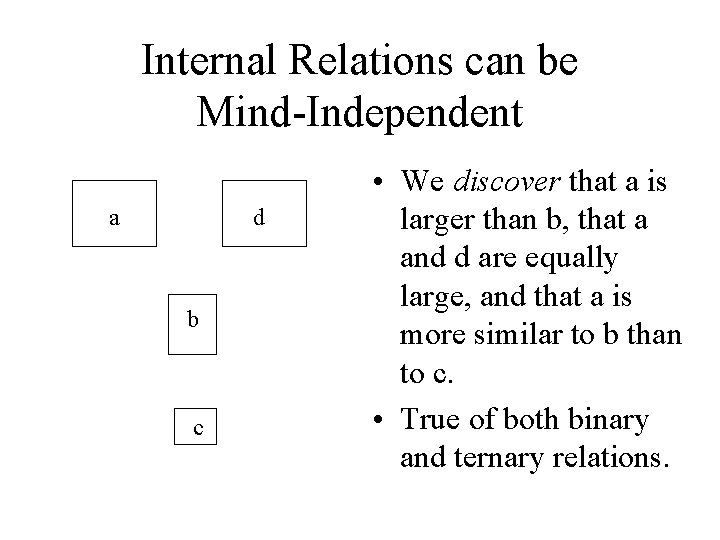
Internal Relations can be Mind-Independent a d b c • We discover that a is larger than b, that a and d are equally large, and that a is more similar to b than to c. • True of both binary and ternary relations.

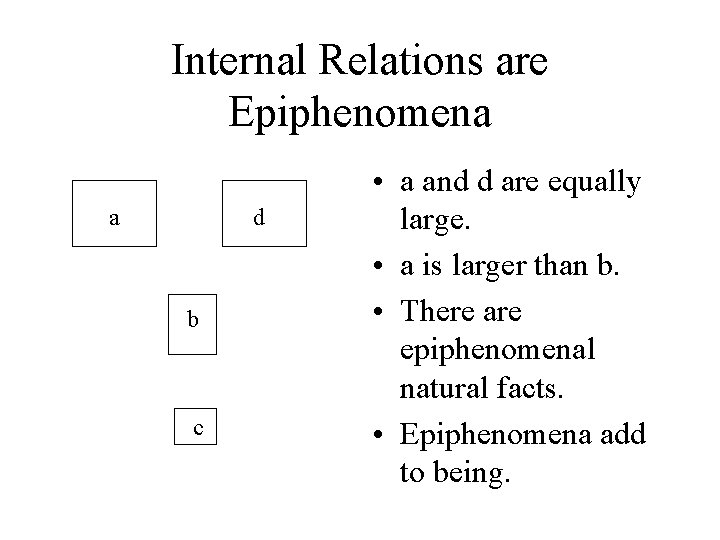
Internal Relations are Epiphenomena a d b c • a and d are equally large. • a is larger than b. • There are epiphenomenal natural facts. • Epiphenomena add to being.

Language Lumps Together blue green y red • What is true of the ordinary language terms, are true of “larger than”, too. • But not of “ 2. 13 times as large as”.

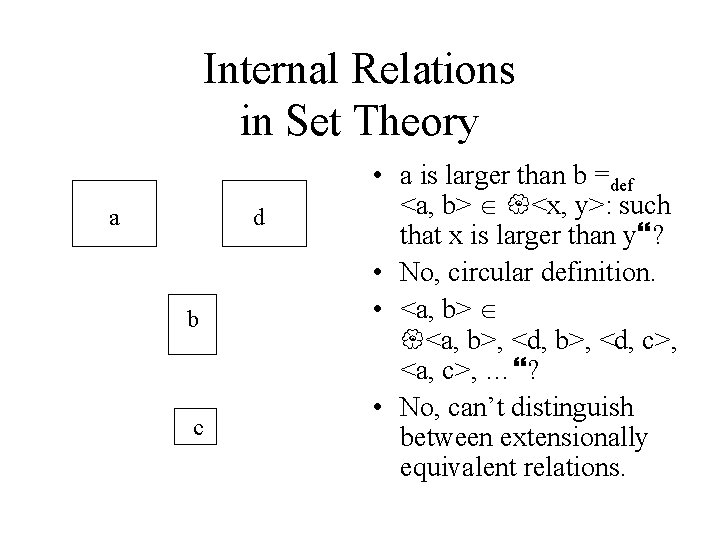
Internal Relations in Set Theory a d b c • a is larger than b =def <a, b> <x, y>: such that x is larger than y ? • No, circular definition. • <a, b>, <d, c>, <a, c>, … ? • No, can’t distinguish between extensionally equivalent relations.

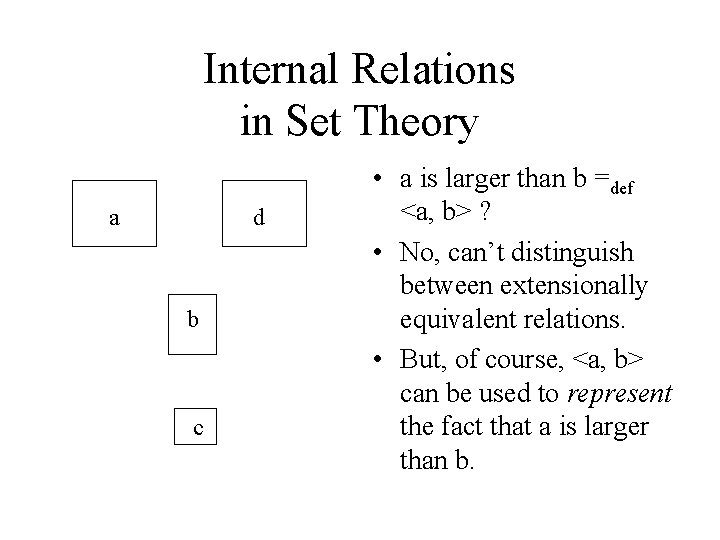
Internal Relations in Set Theory a d b c • a is larger than b =def <a, b> ? • No, can’t distinguish between extensionally equivalent relations. • But, of course, <a, b> can be used to represent the fact that a is larger than b.

Properties of Internal Relations a d b c • ‘larger than’ (L) is asymmetric: xy (Lxy ¬Lyx) • Lab & ¬Lba • ‘equally large’ (E) is symmetric: xy (Exy Eyx) • Ead & Eda

Anti-Symmetrical Relations a d b c • ‘larger than or equal to’ is anti -symmetric: xy (x ≥ y) & (y ≥ x) x = y. • (a ≥ d) & (d ≥ a) & (a = d). • In the individual case there is only symmetry. • (a ≥ b) & ¬(b ≥ a) • In the individual case there is only asymmetry. • No case is anti-symmetric.

Anti-Symmetrical Relations and their Relata • Anti-symmetry: (a ≥ d & d ≥ a) (a = d). • If a and d are numbers, then ‘=’ means numerical identity. • If a and d are quality instances, then ‘=’ means qualitative identity. • If a and d are universals, then ‘=’ means numerical identity.

Representations and Represented: Possible Mistake • There are no anti-symmetrical internal relational universals. • Predicates ( ≥ ) can be anti-symmetric. • Sets of ordered pairs can be anti-symmetric. • Representations of internal relations can be anti -symmetric but internal relations cannot.

Representations and Represented: Logical Constants and the World The spot is red or green • The statement “The spot is red or green” contains a disjunction. • The language-independent world contains no corresponding disjunctive fact.

Can’t Disjunctions be Truthmakers even for Categorical Assertions? • “The spot is red or green. ” • “The spot is red. ” • Isn’t in both cases a disjunction a truthmaker? • v v v. • Answer: In the latter case, we talk as if there is in the world only one property. Language lumps together.

Representations and Represented: Scales and Quantities 0 1 2 3 4 5 6 7 8 9 10 meter ‘ 1 m’ represents the standard meter. ‘ 7 m’ represents all things that are seven times as long as the standard meter. ‘ 0 m’ represents nothing at all, but it is part of the scale.

The End • There are in the language-independent world no disjunctive facts. • There are in the language-independent world no zero quantities. • There are in the language-independent world no anti-symmetrical relations. • In language, there are disjunctions, zero quantities, as well as anti-symmetrical relations.