Probability Sets First we will revise sets Sets
Probability

Sets First we will revise sets
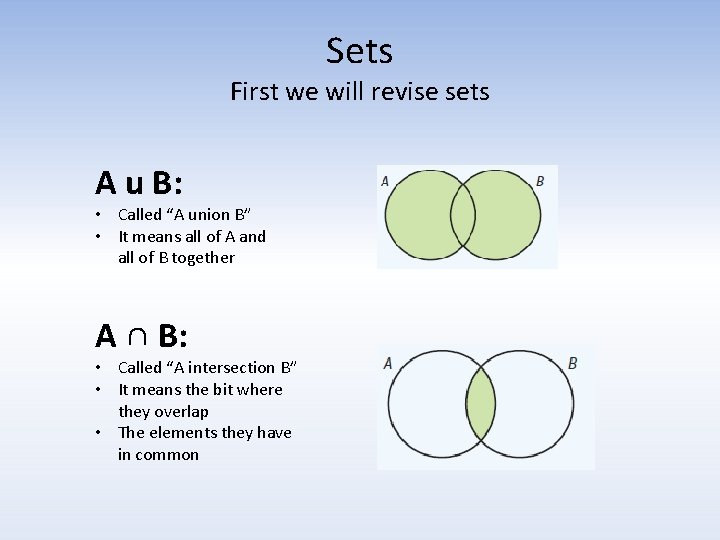
Sets First we will revise sets A u B: • Called “A union B” • It means all of A and all of B together A ∩ B: • Called “A intersection B” • It means the bit where they overlap • The elements they have in common
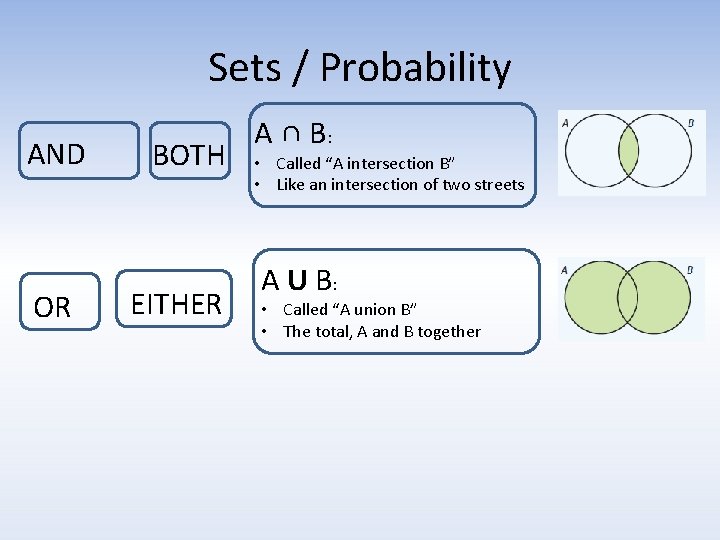
Sets / Probability AND OR BOTH EITHER A ∩ B: • Called “A intersection B” • Like an intersection of two streets A U B: • Called “A union B” • The total, A and B together
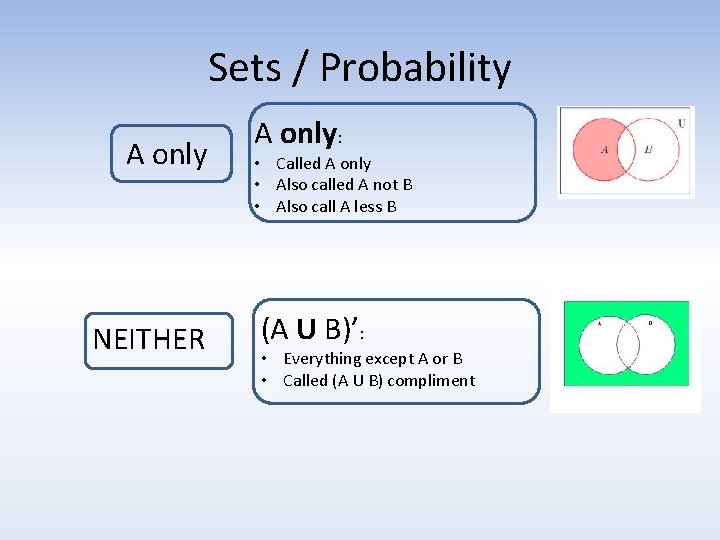
Sets / Probability A only NEITHER A only: • Called A only • Also called A not B • Also call A less B (A U B)’: • Everything except A or B • Called (A U B) compliment

Mutually Exclusive

Mutually Exclusive • They can NOT happen at the same time!!! • The two events have nothing in common • No overlap in the diagram A∩B=0 for mutually exclusive events
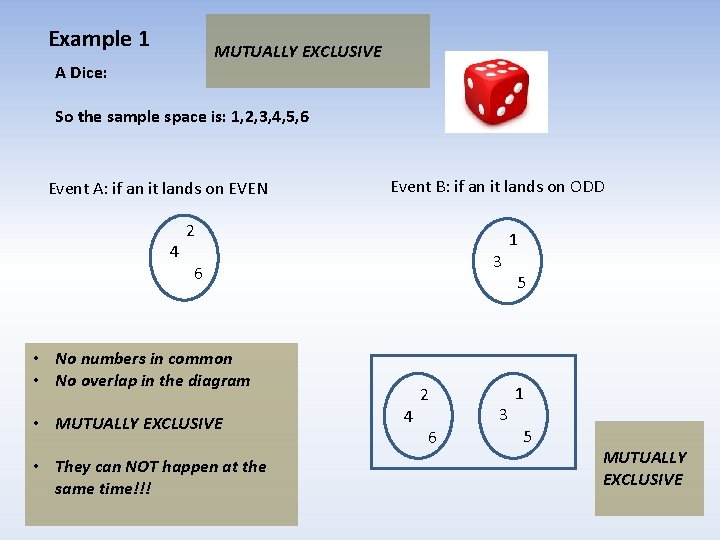
Example 1 MUTUALLY EXCLUSIVE A Dice: So the sample space is: 1, 2, 3, 4, 5, 6 Event A: if an it lands on EVEN 4 Event B: if an it lands on ODD 2 3 6 • No numbers in common • No overlap in the diagram • MUTUALLY EXCLUSIVE • They can NOT happen at the same time!!! 4 2 6 3 1 5 MUTUALLY EXCLUSIVE
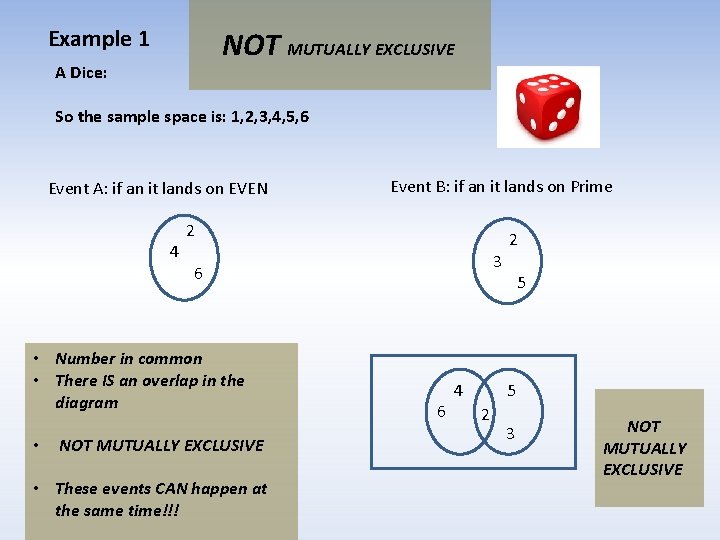
Example 1 NOT MUTUALLY EXCLUSIVE A Dice: So the sample space is: 1, 2, 3, 4, 5, 6 Event A: if an it lands on EVEN 4 2 3 6 • Number in common • There IS an overlap in the diagram • Event B: if an it lands on Prime NOT MUTUALLY EXCLUSIVE • These events CAN happen at the same time!!! 6 4 2 5 5 2 3 NOT MUTUALLY EXCLUSIVE

Conditional Probability

Conditional Probability P(A ∩ B) P(A I B ) = P(B) What does it mean? ? ? • Probability of A given B • Given that it is B, what is the probability of A What is the Probability of Art given that they do business P(A I B ) = P(A ∩ B) P(B) = Art 6 2 7 5 2 Business

Independent events

Independent events • Two events are independent if…… the outcome of one event does not effect the outcome of the other Check for independence: P(A) x P(B) = P(A ∩ B)

Independent events Check for independence: P(A) x P(B) = P(A ∩ B) Where does the above formula come from? ? Think back to our formula for conditional probability P(A I B ) = P(A ∩ B) P(B) For independence we want P (A I B) to be equal to the P(A). In other words we don’t want B to have an affect on the outcome of A So we want P (A I B) = P(A) P(A ∩ B) → P(B) = P(A) Cross multiply gives: P(A) x P(B) = P(A ∩ B)
- Slides: 14