Sets Sets Sets Sets Sets Sets Sets The

Sets

Sets

Sets

Sets

Sets

Sets

Sets The Universal & Complement Sets Let the Universal Set be U U = { 1, 2, 3, 4, 5, 6, 7, 8, 9} and a set A = { 2, 3, 4, 5, 6}. Then, the complement of A is denoted by Ac or A'. Ac = {1, 7, 8, 9}. We can show this with the help of Venn diagram

Sets The Empty Set The Empty set is also called the null set, it is the set that contains no elements, and is represented by { } or � Notice that { } and �have the same meaning and should not be combined An empty set should no be written as {�}

Sets The set of all lowercase letters of the English Alphabet is rather long when represented by the Roster Method. If L is chosen as a name for this set, then we can shorten the listing in set L by writing L = {a, b, c, d, …, z} The three dots after the element “d” inticate that the elements in the set continue in the same manner up to tand including the last element “z”

Sets The Notations ∈ and ∉ The symbol ∈ is used to indicate that an object is an element of a set. The symbol ∈ is used to replace the words “is an element of ” The symbol ∉ is used to indicate that an object is not an element of a set. The symbol ∉ is used to replace the words “is not an element of ”

Sets The Set of Natural Numbers N = {1, 2, 3, 4, 5, 6, …} The three dots after the 6 indicate that there is no final element as the list goes on forever

Sets A Set’s Cardinal Number The Cardinal Number of a set A, represented by n(A) is read “n of A” is the number of elements in set A Given the sets a) M = {7, 9, 11, 13}, b) N = {0}, c) O = {13, 14, 15, …, 22, 23} & d) P = a) n(m) = 4 b) n(N) = 1 c) n(O) = 11 d) n(P)=0 [There are no elements in the Null set] �

Sets A Finite vs an Infinite Set A set A is a finite set if n(a) = 0 or n(A) is a natural number. A set that is not finite is called an Infinite set

Sets Equality of Sets Set A is equal to set B means that A and B contain exactly the same elements, regardless of order or possible repetition of elements. We symbolize the equality of sets using the statement A=B

Sets Equivalence of Sets Set A is equivalent to set B means that A and B contain the same number of elements. For equivalence of sets n(A) = n(B)

Sets

Sets Q-1: Value of set U = {2, 4, 6, 7, 8, 9, 10} and A = {7, 8, 9, 10} and B = {8, 9, 10}. Find the complement of A, complement of B, complement of A union B. Solution: Step 1: Given U = {2, 4, 6, 7, 8, 9, 10} A = {7, 8, 9, 10} B = {8, 9, 10} Step 2: The element of set U is {2, 4, 6, 7, 8, 9, 10}. The element that does not belong to A is {2, 4, 6}. Complement of A is {2, 4, 6}. Step 3: Complement of B is {2, 4, 6, 7} Step 4: Complement of AB is {2, 4, 6, 8, 9, 10}.

Sets Q-2: Values of set U = {3, 5, 7, 8, 9, 10, 12} and A = {8, 9, 10, 12}. Find the compliment of A. Solution Step 1: Given. U = {3, 5, 7, 8, 9, 10, 12} A = {8, 9, 10, 12} Step 2: The element of set U is {3, 5, 7, 8, 9, 10, 12}. Elements {3, 5, 7} does not belong to the set A. So, A’ = {3, 5, 7} Step 3: Complement of A is {3, 5, 7}

Sets Q-3: Values of set U = {1, 4, 6, 7, 8, 10} and A = {6, 7, 8}. Find the complement of A Solution Step 1: Given U = {1, 4, 6, 7, 8, 10} A = {6, 7, 8} Step 2: The element of set U is {1, 4, 6, 7, 8, 10}. Elements {1, 4, 10} does not belong to the set A. A’ is {1, 4, 10}. Step 3: Complement of A is {1, 4, 10}.

Sets & Venn Diagrams

Sets & Venn Diagrams

Sets & Venn Diagrams

Sets & Venn Diagrams

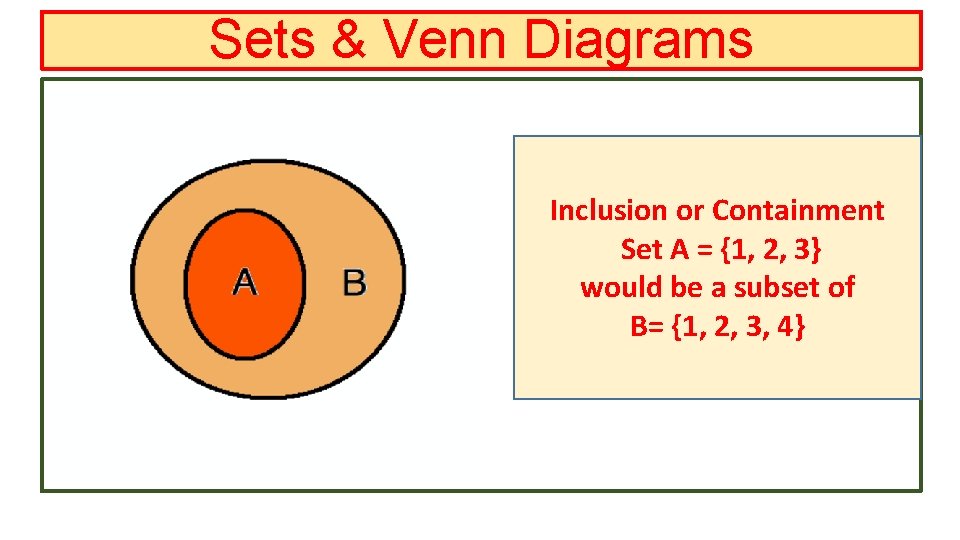
Sets & Venn Diagrams Inclusion or Containment Set A = {1, 2, 3} would be a subset of B= {1, 2, 3, 4}

Sets

Sets & Venn Diagrams

Sets

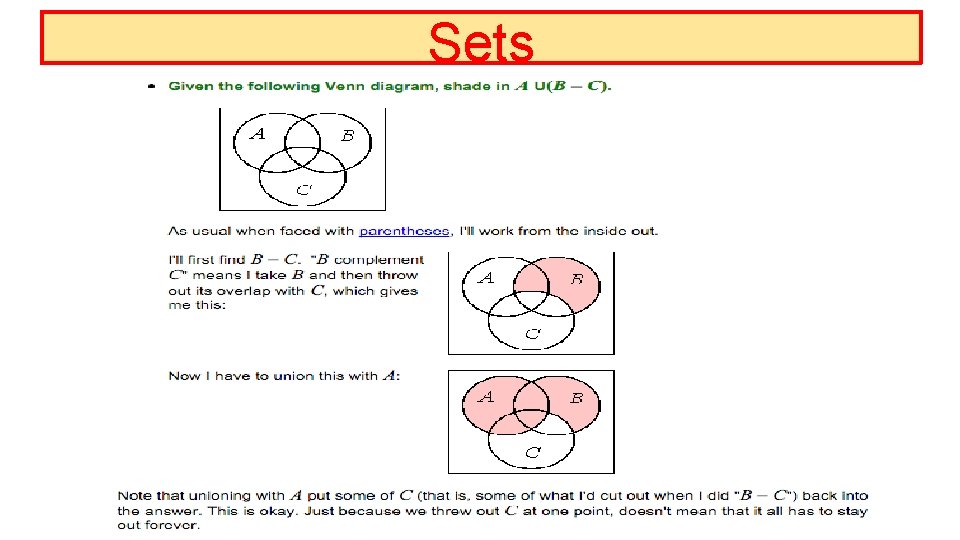
Sets Given the following Venn Diagram, shade in [(B U C) - A] Work from the inside out, do the (B U C) Then do the complement A part by cutting out the overlap with A

Sets Given the following Venn Diagram, shade in ~ [(B U C) - A] Work from the inside out, do the (B U C) Then do the complement A part by cutting out the overlap with A The tilde, in this context, says that I now want to find the complement of what I've shaded. There are two kinds of complement in this problem. The set-subtraction complement in the previous step throws out any overlap between two given sets. But the kind of complement we see in this step, the "not" complement, means "throw out everything you have now and take everything else in the universe".

Sets

Sets

Sets

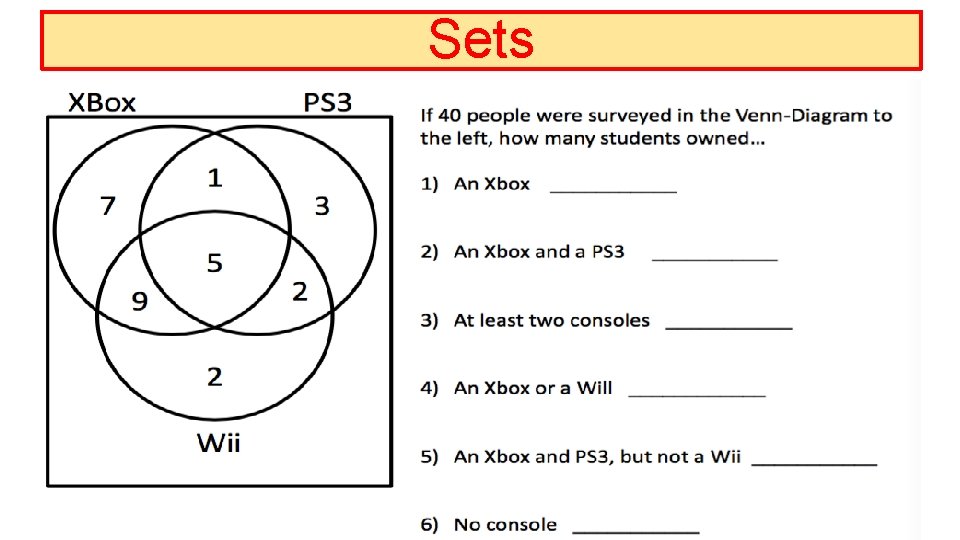
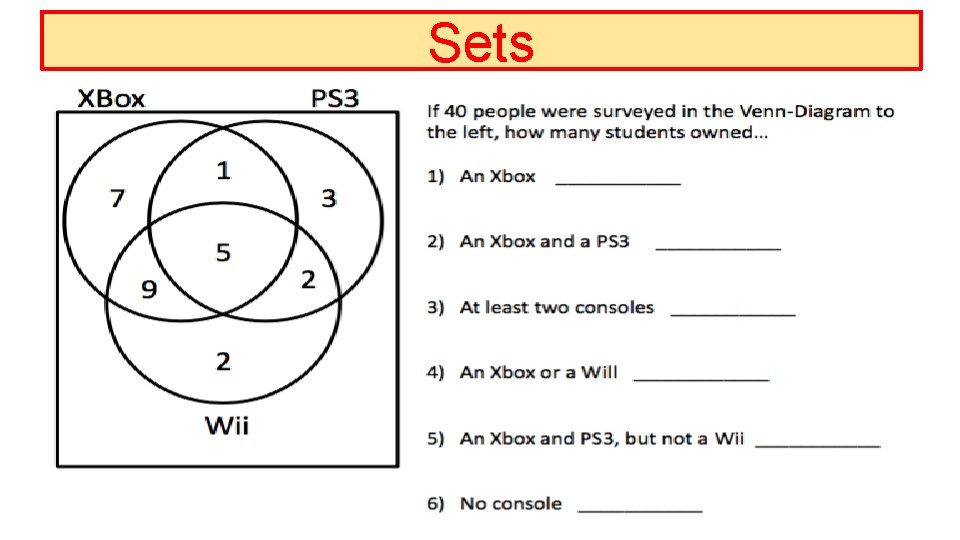
Sets & Venn Diagrams Out of 19 students surveyed, 2 did not own an Xbox or PS 3, 6 students owned a PS 3 and an Xbox, and 14 students owned a PS 3. How many Students owned an Xbox? _______ Only a PS 3? ____ Both Consoles? _______

Sets

Sets

Sets

Sets

Sets

Sets

Sets

Sets

Sets

Sets

Sets

Sets

Sets

Sets

Sets

Sets

Sets

Sets

Sets

Sets

Sets

Sets

Sets

Sets

Sets Natural Numbers: