USING SETS IN LINGO What Are Sets Sets












- Slides: 24

USING SETS IN LINGO What Are Sets? Sets are simply groups of related objects. A set might be a list of products, trucks, or employees. Each member in the set may have one or more characteristics. For example, each product in a set of products might have a price attribute; each truck in a set of trucks might have a capacity attribute; and each employee in a set of employees might have a salary attribute.

Why Use Sets? LINGO’s language allows you to express your largest models very quickly and easily. Types of Sets LINGO recognizes two kinds of sets: primitive and derived sets. Primitive Sets: A primitive set is a set composed only of objects that can’t be reduced. To define a primitive set , you specify: • The name of the set. • Optionally, its members (objects contained in the set). • Optionally, any attributes the members of the set may have.

A primitive set has the following syntax: SETS: setname / member_list / : attribute_list; ENDSETS The set name : is a name you choose to designate the set. A member list : is a list of the members that represent the set. If the set members are included in the set definition, they may be listed either explicitly or implicitly. When listing members explicitly, you enter a unique name for each member for example we could have used an explicit member list to define the set WAREHOUSES in the sets section as follows: SETS: WAREHOUSES / WH 1 WH 2 WH 3 WH 4 WH 5 WH 6/: CAPACITY; ENDSETS

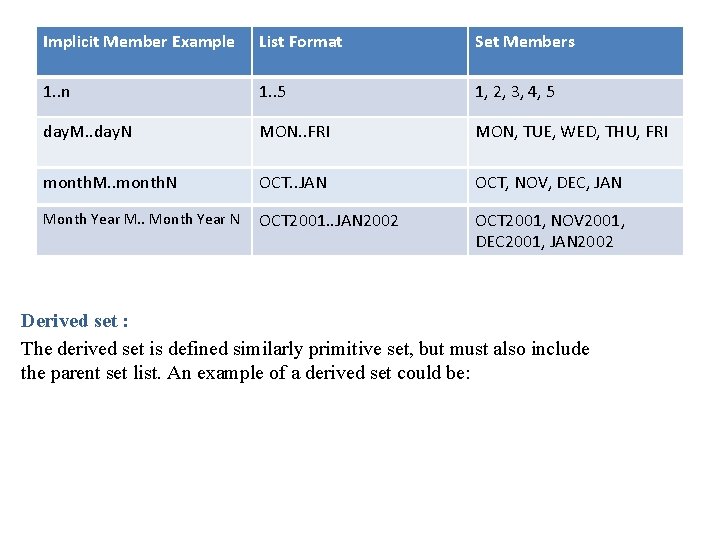
Implicit Member Example List Format Set Members 1. . n 1. . 5 1, 2, 3, 4, 5 day. M. . day. N MON. . FRI MON, TUE, WED, THU, FRI month. M. . month. N OCT. . JAN OCT, NOV, DEC, JAN Month Year M. . Month Year N OCT 2001. . JAN 2002 OCT 2001, NOV 2001, DEC 2001, JAN 2002 Derived set : The derived set is defined similarly primitive set, but must also include the parent set list. An example of a derived set could be:

SETS: PRODUCT / A B/; MACHINE / M N/; WEEK / 1 2/; ALLOWED (PRODUCT, MACHINE, WEEK) ; ENDSETS Sets PRODUCT, MACHINE, and WEEK are primitive sets, while ALLOWED is derived from parent sets, PRODUCT, MACHINE, and WEEK. Taking all the combinations of members from the three parent sets, we come up with the following members in the ALLOWED set:

USING DATA IN LINGO: LINGO provides a separate section called the DATA section in which values can be defined for different variables. The DATA section begins with the tag DATA: and ends with the tag ENDDATA. Statements within the DATA section follow the syntax: object_list = value_list; Example 1: SETS: WAREHOUSES / 1. . NUMBER_OF_WH/: CAPACITY; ENDSETS DATA: NUMBER_OF_WH = 6; ENDDATA

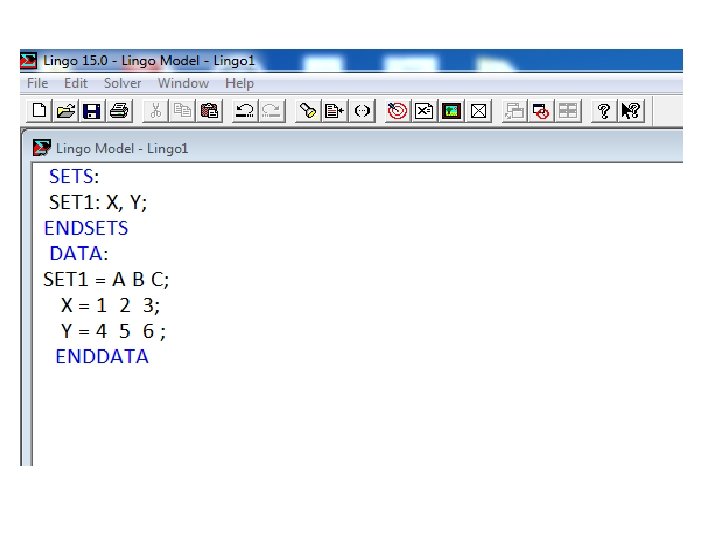
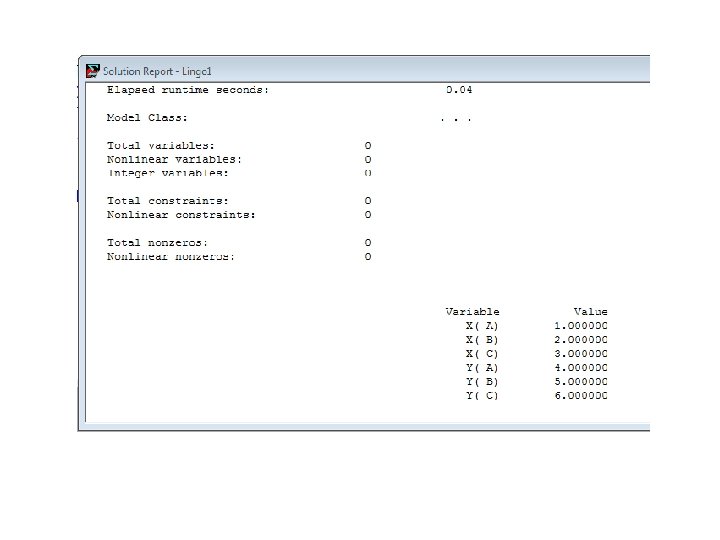
EXAMPLE 2: consider the following model: SETS: SET 1: X, Y; ENDSETS DATA: SET 1 = A B C; X = 1 2 3; Y=4 5 6; DATA END We have two attributes X and Y defined on the set SET 1. The three values of X are set to 1, 2, and 3, while Y is set to 4, 5, and 6.



Set Looping Functions There are currently four set looping functions in LINGO. The syntax for a set looping function is: @function(setname [ (set_index_list) [|conditional_qualifier]] : expression_list); The names of the functions and their uses are: @FOR Used to generate constraints over members of a set. @SUM Computes the sum of an expression over all members of a set. @MIN Computes the minimum of an expression over all members of a set. @MAX Computes the maximum of an expression over all members of a set.

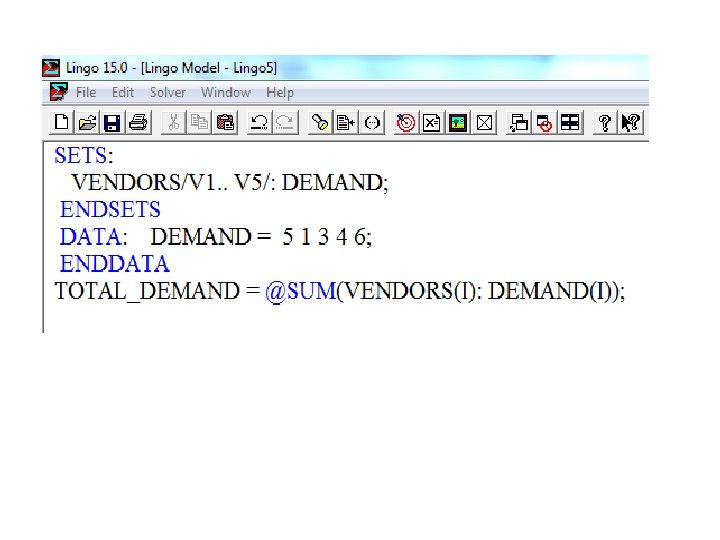
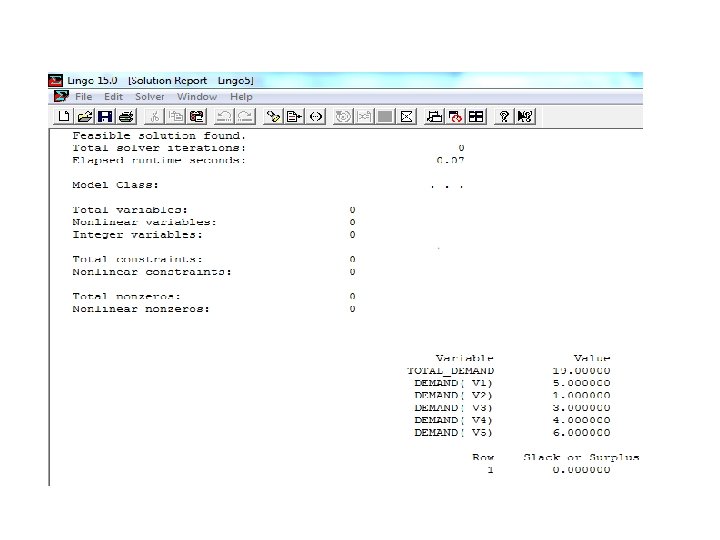
@SUM Set Looping Function Example 3: Consider the model: MODEL: SETS: VENDORS/V 1. . V 5/: DEMAND; ENDSETS DATA: DEMAND = 5 1 3 4 6; ENDDATA TOTAL_DEMAND = @SUM(VENDORS(J): DEMAND(J)); Note that: LINGO evaluates the @SUM function by first initializing an internal accumulator to zero. LINGO then begins looping over the members in the VENDORS set. The set index variable, J, is set to the first member of VENDORS (i. e. , V 1) and DEMAND (V 1) is then added to the accumulator. This process continues until all DEMAND values have been added to the accumulator. The value of the sum is then stored in the TOTAL_DEMAND variable.



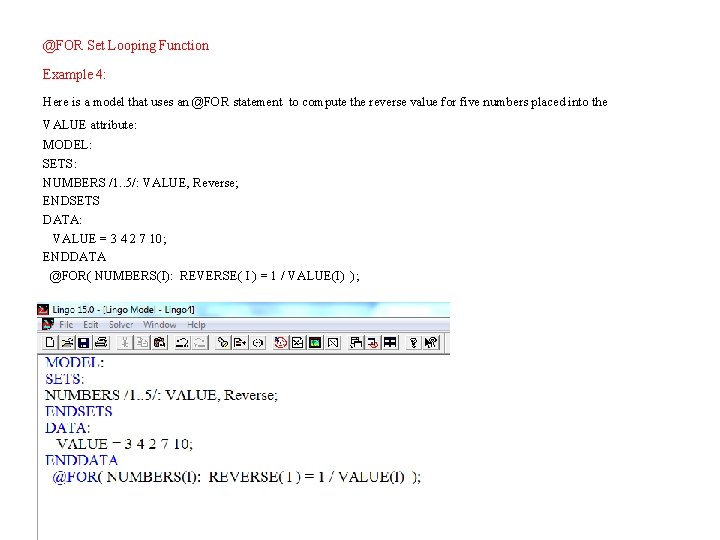
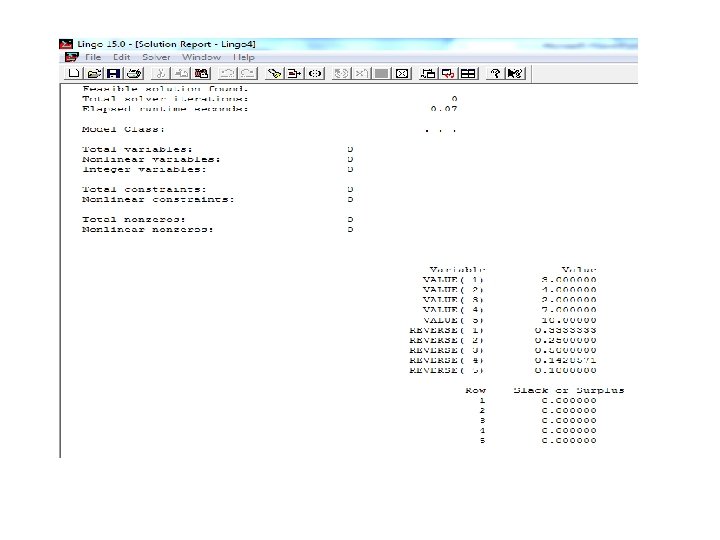
@FOR Set Looping Function Example 4: Here is a model that uses an @FOR statement to compute the reverse value for five numbers placed into the VALUE attribute: MODEL: SETS: NUMBERS /1. . 5/: VALUE, Reverse; ENDSETS DATA: VALUE = 3 4 2 7 10; ENDDATA @FOR( NUMBERS(I): REVERSE( I ) = 1 / VALUE(I) );


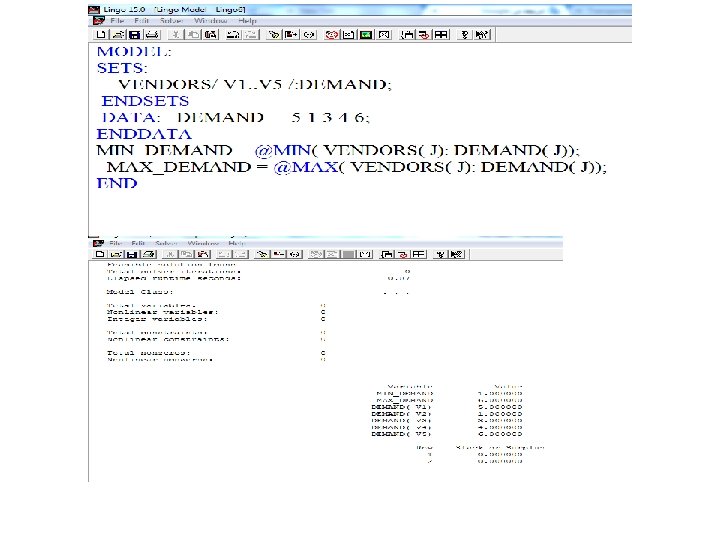
@MIN and @MAX Set Looping Functions Again, consider the Example 3: SETS: VENDORS/ V 1. . V 5 /: DEMAND; ENDSETS DATA: DEMAND = 5 1 3 4 6; ENDDATA MIN_DEMAND = @MIN( VENDORS( J): DEMAND( J)); MAX_DEMAND = @MAX( VENDORS( J): DEMAND( J)); END We can write above example by this method SETS: VENDORS: DEMAND; ENDSETS DATA: VENDORS, DEMAND = V 1, 5 V 2, 1 V 3, 3 V 4, 4 V 5, 6; ENDDATA MIN_DEMAND = @MIN( VENDORS( J): DEMAND( J)); MAX_DEMAND = @MAX( VENDORS( J): DEMAND( J)); END


Using Variable Domain Functions These variable domain functions are: @GIN –any positive integer value @BIN –a binary value ( 0 or 1) @FREE –any positive or negative real value @BND –any value within the specified bounds

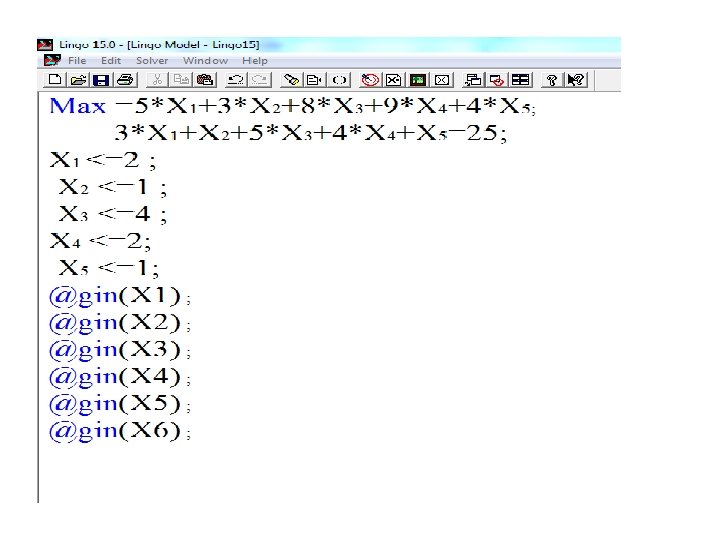
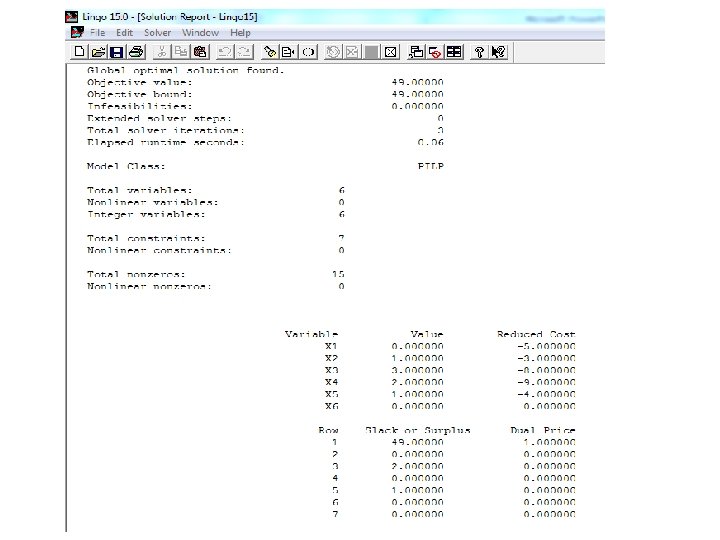
Example : Solve the following knapsack problem by using lingo software : Max 5 X 1+3 X 2+8 X 3+9 X 4+4 X 5 3 X 1+X 2+5 X 3+4 X 4+X 5=25 0≤X 1 ≤ 2 , 0 ≤X 2 ≤ 1 , 0 ≤X 3 ≤ 4 , 0 ≤X 4 ≤ 2, 0 ≤X 5 ≤ 1 X 1, X 2, X 3, X 4, and X 5 are integer.



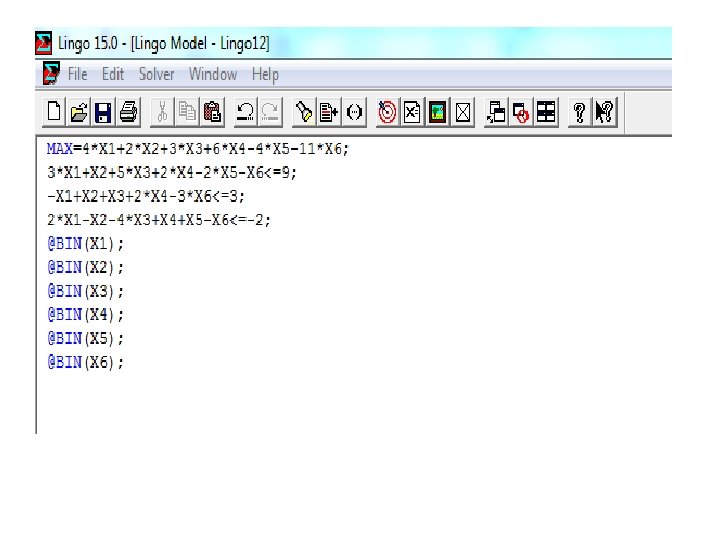
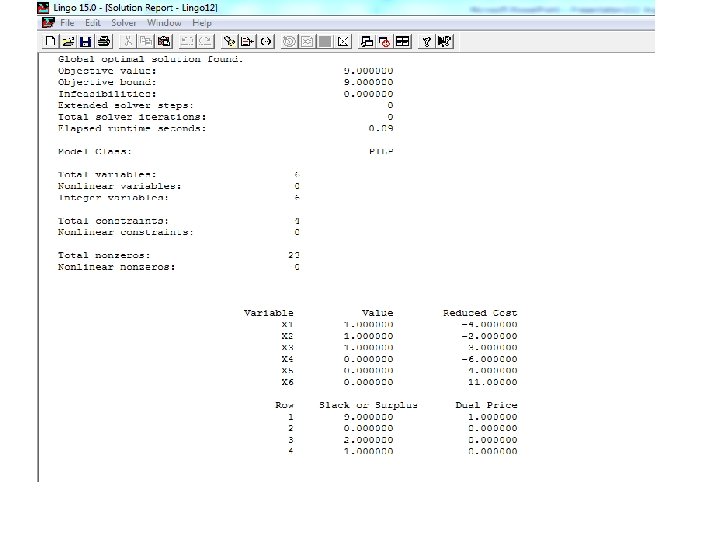
Example : Solve the following LP problem MAX 4 X 1+2 X 2+3 X 3+6 X 4 -4 X 5 -11 X 6 3 X 1+X 2+5 X 3+2 X 4 -2 X 5 -X 6 ≤ 9 -X 1+X 2+X 3+2 X 4 -3 X 6 ≤ 3 2 X 1 -X 2 -4 X 3+X 4+X 5 -X 6 ≤ -2 X 1, X 2, X 3, X 4, X 5 and X 6 are binary variables

