11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND




















































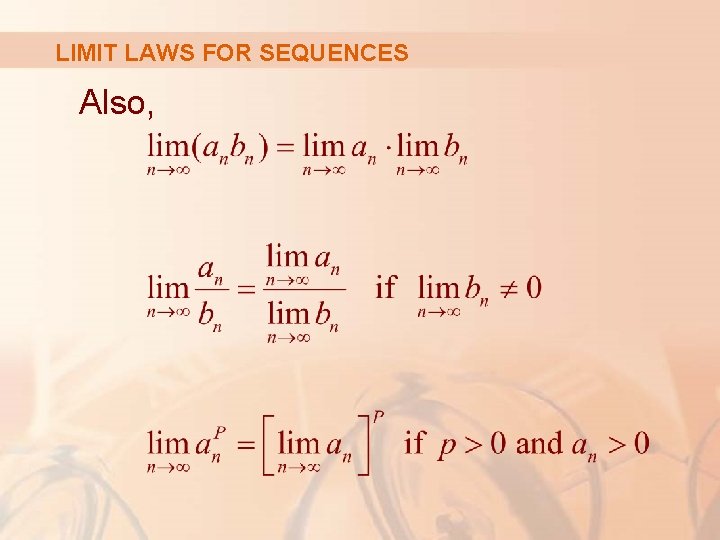



































































- Slides: 126

11 INFINITE SEQUENCES AND SERIES

INFINITE SEQUENCES AND SERIES Infinite sequences and series were introduced briefly in A Preview of Calculus in connection with Zeno’s paradoxes and the decimal representation of numbers.

INFINITE SEQUENCES AND SERIES Their importance in calculus stems from Newton’s idea of representing functions as sums of infinite series. § For instance, in finding areas, he often integrated a function by first expressing it as a series and then integrating each term of the series.

INFINITE SEQUENCES AND SERIES We will pursue his idea in Section 11. 10 in order to integrate such functions as § Recall that we have previously been unable to do this. 2 -x e.

INFINITE SEQUENCES AND SERIES Many of the functions that arise in mathematical physics and chemistry, such as Bessel functions, are defined as sums of series. § It is important to be familiar with the basic concepts of convergence of infinite sequences and series.

INFINITE SEQUENCES AND SERIES Physicists also use series in another way, as we will see in Section 11. 11 § In studying fields as diverse as optics, special relativity, and electromagnetism, they analyze phenomena by replacing a function with the first few terms in the series that represents it.

INFINITE SEQUENCES AND SERIES 11. 1 Sequences In this section, we will learn about: Various concepts related to sequences.

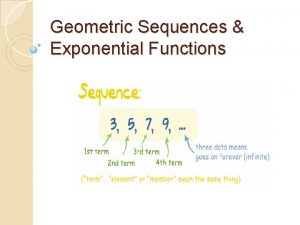
SEQUENCE A sequence can be thought of as a list of numbers written in a definite order: a 1, a 2, a 3, a 4, …, an, … § The number a 1 is called the first term, a 2 is the second term, and in general an is the nth term.

SEQUENCES We will deal exclusively with infinite sequences. § So, each term an will have a successor an+1.

SEQUENCES Notice that, for every positive integer n, there is a corresponding number an. So, a sequence can be defined as: § A function whose domain is the set of positive integers

SEQUENCES However, we usually write an instead of the function notation f(n) for the value of the function at the number n.

SEQUENCES Notation The sequence { a 1, a 2, a 3, . . . } is also denoted by:

SEQUENCES Example 1 Some sequences can be defined by giving a formula for the nth term.

SEQUENCES Example 1 In the following examples, we give three descriptions of the sequence: 1. Using the preceding notation 2. Using the defining formula 3. Writing out the terms of the sequence

Example 1 a SEQUENCES Preceding Defining Notation Formula Terms of Sequence § In this and the subsequent examples, notice that n doesn’t have to start at 1.

Example 1 b SEQUENCES Preceding Defining Terms of Notation Formula Sequence

Example 1 c SEQUENCES Preceding Defining Notation Formula Terms of Sequence

Example 1 d SEQUENCES Preceding Defining Notation Formula Terms of Sequence

SEQUENCES Example 2 Find a formula for the general term an of the sequence assuming the pattern of the first few terms continues.

SEQUENCES We are given that: Example 2

SEQUENCES Example 2 Notice that the numerators of these fractions start with 3 and increase by 1 whenever we go to the next term. § The second term has numerator 4 and the third term has numerator 5. § In general, the nth term will have numerator n+2.

Example 2 SEQUENCES The denominators are the powers of 5. n § Thus, an has denominator 5.

SEQUENCES Example 2 The signs of the terms are alternately positive and negative. § Hence, we need to multiply by a power of – 1.

SEQUENCES Example 2 In Example 1 b, the factor (– 1)n meant we started with a negative term. Here, we want to start with a positive term.

SEQUENCES Example 2 Thus, we use (– 1)n– 1 or (– 1)n+1. § Therefore,

SEQUENCES Example 3 We now look at some sequences that don’t have a simple defining equation.

SEQUENCES Example 3 a The sequence {pn}, where pn is the population of the world as of January 1 in the year n

SEQUENCES Example 3 b If we let an be the digit in the nth decimal place of the number e, then {an} is a welldefined sequence whose first few terms are: {7, 1, 8, 2, 8, 4, 5, …}

FIBONACCI SEQUENCE Example 3 c The Fibonacci sequence {fn} is defined recursively by the conditions f 1 = 1 f 2 = 1 fn = fn– 1 + fn– 2 § Each is the sum of the two preceding terms. § The first few terms are: {1, 1, 2, 3, 5, 8, 13, 21, …} n≥ 3

FIBONACCI SEQUENCE Example 3 This sequence arose when the 13 th-century Italian mathematician Fibonacci solved a problem concerning the breeding of rabbits. § See Exercise 71.

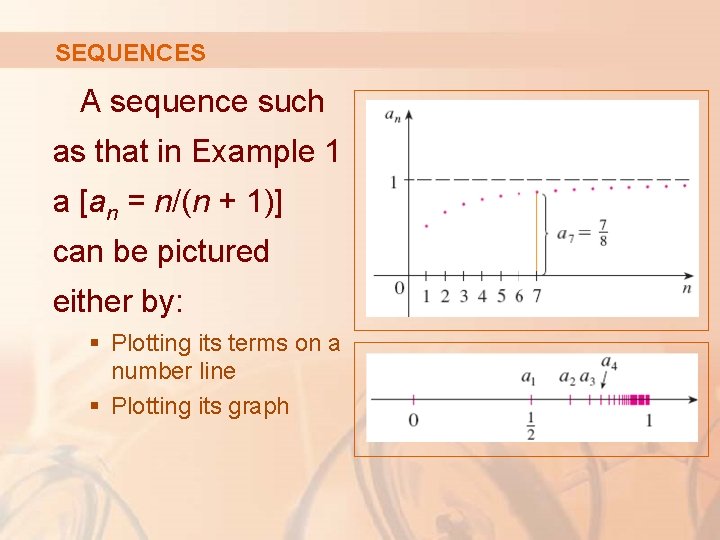
SEQUENCES A sequence such as that in Example 1 a [an = n/(n + 1)] can be pictured either by: § Plotting its terms on a number line § Plotting its graph

SEQUENCES Note that, since a sequence is a function whose domain is the set of positive integers, its graph consists of isolated points with coordinates (1, a 1) (2, a 2) (3, a 3) … (n, an) …

SEQUENCES From either figure, it appears that the terms of the sequence an = n/(n + 1) are approaching 1 as n becomes large.

SEQUENCES In fact, the difference can be made as small as we like by taking n sufficiently large. § We indicate this by writing

SEQUENCES In general, the notation means that the terms of the sequence {an} approach L as n becomes large.

SEQUENCES Notice that the following definition of the limit of a sequence is very similar to the definition of a limit of a function at infinity given in Section 2. 6

LIMIT OF A SEQUENCE Definition 1 A sequence {an} has the limit L, and we write if we can make the terms an as close to L as we like, by taking n sufficiently large. § If exists, the sequence converges (or is convergent). § Otherwise, it diverges (or is divergent).

LIMIT OF A SEQUENCE Here, Definition 1 is illustrated by showing the graphs of two sequences that have the limit L.

LIMIT OF A SEQUENCE A more precise version of Definition 1 is as follows.

Definition 2 LIMIT OF A SEQUENCE A sequence {an} has the limit L, and we write if for every ε > 0 there is a corresponding integer N such that: if n>N then |an – L| < ε

LIMIT OF A SEQUENCE Definition 2 is illustrated by the figure, in which the terms a 1, a 2, a 3, . . . are plotted on a number line.

LIMIT OF A SEQUENCE No matter how small an interval (L – ε, L + ε) is chosen, there exists an N such that all terms of the sequence from a. N+1 onward must lie in that interval.

LIMIT OF A SEQUENCE Another illustration of Definition 2 is given here. § The points on the graph of {an} must lie between the horizontal lines y = L + ε and y = L – ε if n > N.

LIMIT OF A SEQUENCE This picture must be valid no matter how small ε is chosen. § Usually, however, a smaller ε requires a larger N.

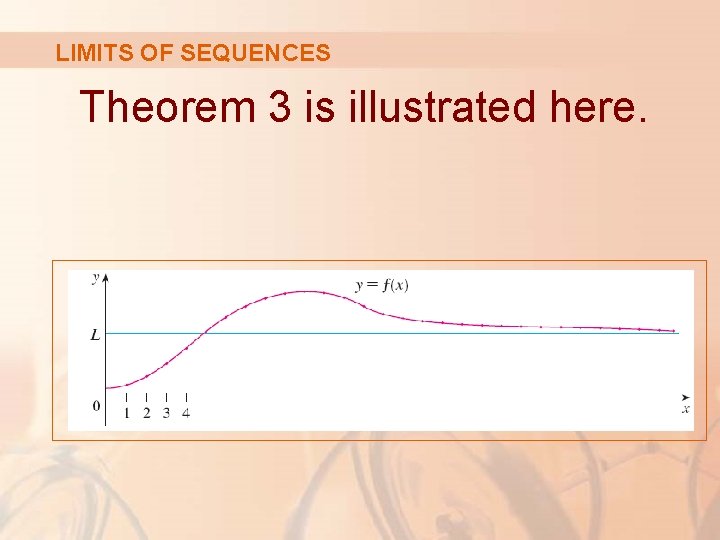
LIMITS OF SEQUENCES If you compare Definition 2 with Definition 7 in Section 2. 6, you will see that the only difference between and is that n is required to be an integer. § Thus, we have the following theorem.

LIMITS OF SEQUENCES If Theorem 3 and f(n) = an when n is an integer, then

LIMITS OF SEQUENCES Theorem 3 is illustrated here.

Equation 4 LIMITS OF SEQUENCES In particular, since we know that when r > 0 (Theorem 5 in Section 2. 6), we have:

LIMITS OF SEQUENCES If an becomes large as n becomes large, we use the notation § The following precise definition is similar to Definition 9 in Section 2. 6

Definition 5 LIMIT OF A SEQUENCE means that, for every positive number M, there is an integer N such that if n>N then an > M

LIMITS OF SEQUENCES If , then the sequence {an} is divergent, but in a special way. § We say that {an} diverges to ∞.

LIMITS OF SEQUENCES The Limit Laws given in Section 2. 3 also hold for the limits of sequences and their proofs are similar.

LIMIT LAWS FOR SEQUENCES Suppose {an} and {bn} are convergent sequences and c is a constant.

LIMIT LAWS FOR SEQUENCES Then,
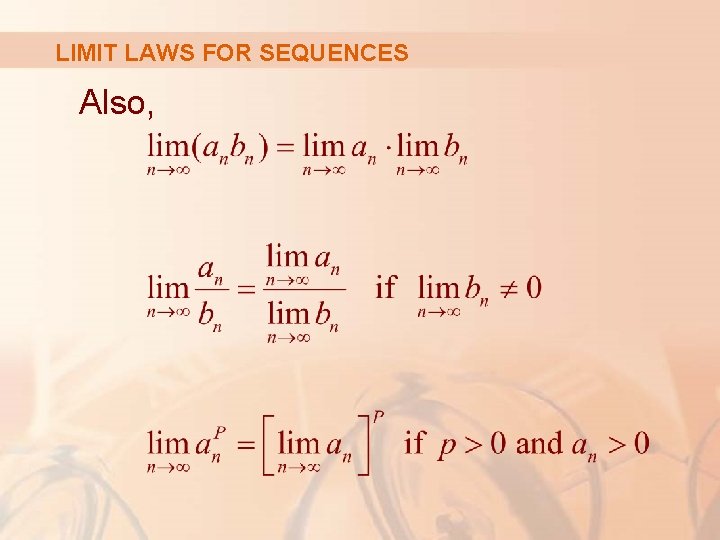
LIMIT LAWS FOR SEQUENCES Also,

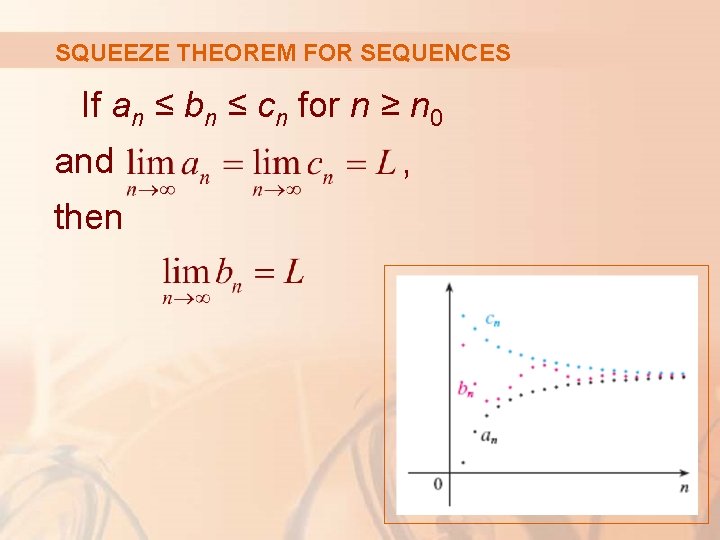
LIMITS OF SEQUENCES The Squeeze Theorem can also be adapted for sequences, as follows.

SQUEEZE THEOREM FOR SEQUENCES If an ≤ bn ≤ cn for n ≥ n 0 and then ,

LIMITS OF SEQUENCES Another useful fact about limits of sequences is given by the following theorem. § The proof is left as Exercise 75.

LIMITS OF SEQUENCES If then Theorem 6

LIMITS OF SEQUENCES Example 4 Find § The method is similar to the one we used in Section 2. 6 § We divide the numerator and denominator by the highest power of n and then use the Limit Laws.

LIMITS OF SEQUENCES Example 4 Thus, § Here, we used Equation 4 with r = 1.

LIMITS OF SEQUENCES Example 5 Calculate § Notice that both the numerator and denominator approach infinity as n → ∞.

LIMITS OF SEQUENCES Example 5 Here, we can’t apply l’Hospital’s Rule directly. § It applies not to sequences but to functions of a real variable.

LIMITS OF SEQUENCES Example 5 However, we can apply l’Hospital’s Rule to the related function f(x) = (ln x)/x and obtain:

LIMITS OF SEQUENCES Example 5 Therefore, by Theorem 3, we have:

LIMITS OF SEQUENCES Example 6 Determine whether the sequence an = (– 1)n is convergent or divergent.

LIMITS OF SEQUENCES Example 6 If we write out the terms of the sequence, we obtain: {– 1, 1, – 1, …}

LIMITS OF SEQUENCES Example 6 The graph of the sequence is shown. § The terms oscillate between 1 and – 1 infinitely often. § Thus, an does not approach any number.

LIMITS OF SEQUENCES Thus, Example 6 does not exist. That is, the sequence {(– 1)n} is divergent.

LIMITS OF SEQUENCES Evaluate § § Thus, by Theorem 6, Example 7 if it exists.

LIMITS OF SEQUENCES The following theorem says that, if we apply a continuous function to the terms of a convergent sequence, the result is also convergent.

LIMITS OF SEQUENCES If Theorem 7 and the function f is continuous at L, then § The proof is left as Exercise 76.

LIMITS OF SEQUENCES Example 8 Find § The sine function is continuous at 0. § Thus, Theorem 7 enables us to write:

LIMITS OF SEQUENCES Example 9 Discuss the convergence of the sequence an = n!/nn, where n! = 1. 2. 3. …. n

LIMITS OF SEQUENCES Example 9 Both the numerator and denominator approach infinity as n → ∞. However, here, we have no corresponding function for use with l’Hospital’s Rule. § x! is not defined when x is not an integer.

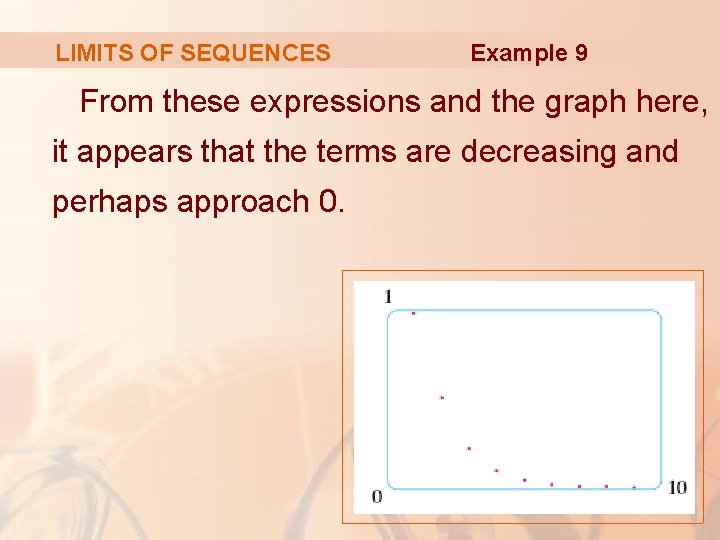
LIMITS OF SEQUENCES Example 9 Let’s write out a few terms to get a feeling for what happens to an as n gets large:

LIMITS OF SEQUENCES Therefore, E. g. 9—Equation 8

LIMITS OF SEQUENCES Example 9 From these expressions and the graph here, it appears that the terms are decreasing and perhaps approach 0.

LIMITS OF SEQUENCES Example 9 To confirm this, observe from Equation 8 that § Notice that the expression in parentheses is at most 1 because the numerator is less than (or equal to) the denominator.

LIMITS OF SEQUENCES Example 9 Thus, 0 < an ≤ § We know that 1/n → 0 as n → ∞. § Therefore an → 0 as n → ∞ by the Squeeze Theorem.

LIMITS OF SEQUENCES Example 10 For what values of r is the sequence {r n} convergent? § From Section 2. 6 and the graphs of the exponential functions in Section 1. 5, we know that for a > 1 and for 0 < a < 1.

LIMITS OF SEQUENCES Example 10 Thus, putting a = r and using Theorem 3, we have: § It is obvious that

LIMITS OF SEQUENCES Example 10 If – 1 < r < 0, then 0 < |r | < 1. § Thus, § Therefore, by Theorem 6,

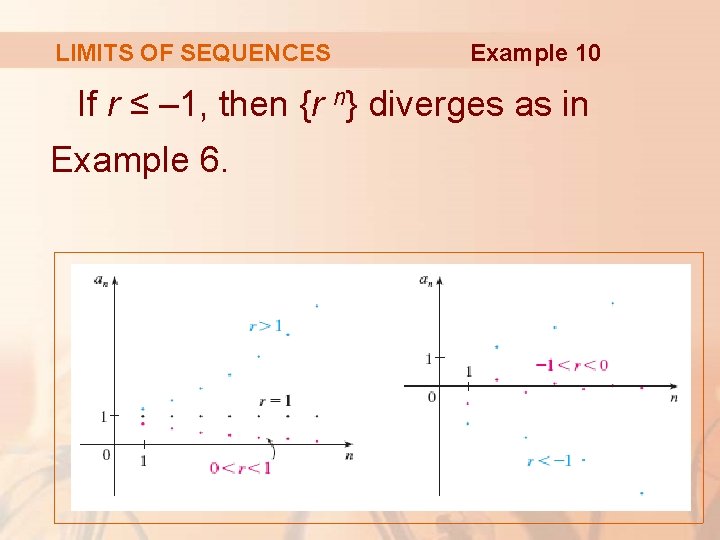
LIMITS OF SEQUENCES Example 10 If r ≤ – 1, then {r n} diverges as in Example 6.

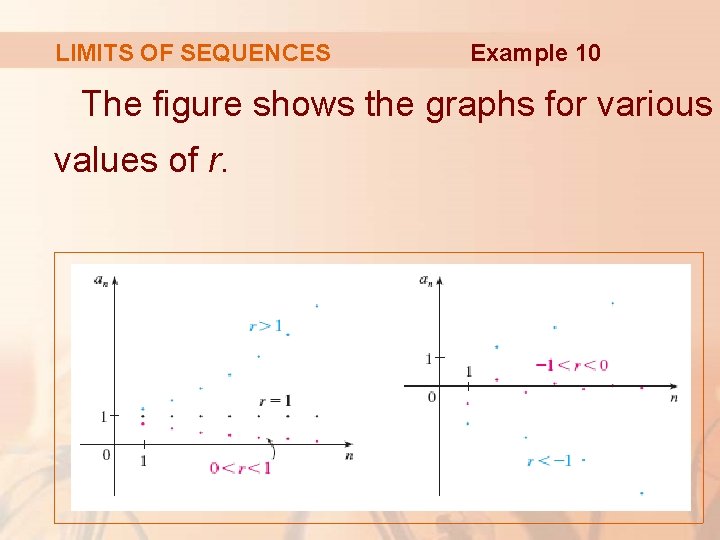
LIMITS OF SEQUENCES Example 10 The figure shows the graphs for various values of r.

LIMITS OF SEQUENCES Example 10 The case r = – 1 was shown earlier.

LIMITS OF SEQUENCES The results of Example 10 are summarized for future use, as follows.

LIMITS OF SEQUENCES Equation 9 The sequence {r n} is convergent if – 1 < r ≤ 1 and divergent for all other values of r.

LIMITS OF SEQUENCES Definition 10 A sequence {an} is called: § Increasing, if an < an+1 for all n ≥ 1, that is, a 1 < a 2 < a 3 < · · · § Decreasing, if an > an+1 for all n ≥ 1 § Monotonic, if it is either increasing or decreasing

DECREASING SEQUENCES The sequence Example 11 is decreasing because and so an > an+1 for all n ≥ 1.

DECREASING SEQUENCES Show that the sequence is decreasing. Example 12

DECREASING SEQUENCES E. g. 12—Solution 1 We must show that an+1 < an, that is,

DECREASING SEQUENCES E. g. 12—Solution 1 This inequality is equivalent to the one we get by cross-multiplication:

DECREASING SEQUENCES E. g. 12—Solution 1 Since n ≥ 1, we know that the inequality n 2 + n > 1 is true. § Therefore, an+1 < an. § Hence, {an} is decreasing.

DECREASING SEQUENCES Consider the function E. g. 12—Solution 2

DECREASING SEQUENCES E. g. 12—Solution 2 Thus, f is decreasing on (1, ∞). § Hence, f(n) > f(n + 1). § Therefore, {an} is decreasing.

BOUNDED SEQUENCES Definition 11 A sequence {an} is bounded: § Above, if there is a number M such that an ≤ M for all n ≥ 1 § Below, if there is a number m such that m ≤ an for all n ≥ 1 § If it is bounded above and below

BOUNDED SEQUENCES For instance, § The sequence an = n is bounded below (an > 0) but not above. § The sequence an = n/(n+1) is bounded because 0 < an < 1 for all n.

BOUNDED SEQUENCES We know that not every bounded sequence is convergent. § For instance, the sequence an = (– 1)n satisfies – 1 ≤ an ≤ 1 but is divergent from Example 6.

BOUNDED SEQUENCES Similarly, not every monotonic sequence is convergent (an = n → ∞).

BOUNDED SEQUENCES However, if a sequence is both bounded and monotonic, then it must be convergent. § This fact is proved as Theorem 12. § However, intuitively, you can understand why it is true by looking at the following figure.

BOUNDED SEQUENCES If {an} is increasing and an ≤ M for all n, then the terms are forced to crowd together and approach some number L.

BOUNDED SEQUENCES The proof of Theorem 12 is based on the Completeness Axiom for the set of real numbers. § This states that, if S is a nonempty set of real numbers that has an upper bound M (x ≤ M for all x in S), then S has a least upper bound b.

BOUNDED SEQUENCES This means: § b is an upper bound for S. § However, if M is any other upper bound, then b ≤ M.

BOUNDED SEQUENCES The Completeness Axiom is an expression of the fact that there is no gap or hole in the real number line.

MONOTONIC SEQ. THEOREM Theorem 12 Every bounded, monotonic sequence is convergent.

MONOTONIC SEQ. THEOREM Theorem 12—Proof Suppose {an} is an increasing sequence. § Since {an} is bounded, the set S = {an|n ≥ 1} has an upper bound. § By the Completeness Axiom, it has a least upper bound L.

MONOTONIC SEQ. THEOREM Theorem 12—Proof Given ε > 0, L – ε is not an upper bound for S (since L is the least upper bound). § Therefore, a. N > L – ε for some integer N

MONOTONIC SEQ. THEOREM Theorem 12—Proof However, the sequence is increasing. So, an ≥ a. N for every n > N. § Thus, if n > N, we have an > L – ε § Since an ≤ L, thus 0 ≤ L – an < ε

MONOTONIC SEQ. THEOREM Theorem 12—Proof Thus, |L – an| < ε Therefore, whenever n > N

MONOTONIC SEQ. THEOREM Theorem 12—Proof A similar proof (using the greatest lower bound) works if {an} is decreasing.

MONOTONIC SEQ. THEOREM The proof of Theorem 12 shows that a sequence that is increasing and bounded above is convergent. § Likewise, a decreasing sequence that is bounded below is convergent.

MONOTONIC SEQ. THEOREM This fact is used many times in dealing with infinite series.

MONOTONIC SEQ. THEOREM Example 13 Investigate the sequence {an} defined by the recurrence relation

MONOTONIC SEQ. THEOREM Example 13 We begin by computing the first several terms: § These initial terms suggest the sequence is increasing and the terms are approaching 6.

MONOTONIC SEQ. THEOREM Example 13 To confirm that the sequence is increasing, we use mathematical induction to show that an+1 > an for all n ≥ 1. § Mathematical induction is often used in dealing with recursive sequences.

MONOTONIC SEQ. THEOREM Example 13 That is true for n = 1 because a 2 = 4 > a 1.

MONOTONIC SEQ. THEOREM Example 13 If we assume that it is true for n = k, we have: § Hence, and § Thus,

MONOTONIC SEQ. THEOREM Example 13 We have deduced that an+1 > an is true for n = k + 1. Therefore, the inequality is true for all n by induction.

MONOTONIC SEQ. THEOREM Example 13 Next, we verify that {an} is bounded by showing that an < 6 for all n. § Since the sequence is increasing, we already know that it has a lower bound: an ≥ a 1 = 2 for all n

MONOTONIC SEQ. THEOREM Example 13 We know that a 1 < 6. So, the assertion is true for n = 1.

MONOTONIC SEQ. THEOREM Example 13 Suppose it is true for n = k. § Then, § Thus, and § Hence,

MONOTONIC SEQ. THEOREM Example 13 This shows, by mathematical induction, that an < 6 for all n.

MONOTONIC SEQ. THEOREM Example 13 Since the sequence {an} is increasing and bounded, Theorem 12 guarantees that it has a limit. § However, theorem doesn’t tell us what the value of the limit is.

MONOTONIC SEQ. THEOREM Example 13 Nevertheless, now that we know exists, we can use the recurrence relation to write:

MONOTONIC SEQ. THEOREM Example 13 Since an → L, it follows that an+1 → L, too (as n → ∞, n + 1 → ∞ too). § Thus, we have: § Solving this equation for L, we get L = 6, as predicted.
 Maclaurin polynomial
Maclaurin polynomial Infinite diversity in infinite combinations
Infinite diversity in infinite combinations Arithmetic and geometric sequences and series
Arithmetic and geometric sequences and series Differentiate finite sequence from an infinite sequence
Differentiate finite sequence from an infinite sequence 10-2 practice arithmetic sequences and series
10-2 practice arithmetic sequences and series Unit 10 sequences and series homework 1 answers
Unit 10 sequences and series homework 1 answers Chapter 12 sequences and series answers
Chapter 12 sequences and series answers 10-3 geometric sequences and series
10-3 geometric sequences and series Module 12 sequences and series
Module 12 sequences and series 10-3 practice geometric sequences and series answer key
10-3 practice geometric sequences and series answer key 10-2 practice arithmetic sequences and series
10-2 practice arithmetic sequences and series 10-1 sequences series and sigma notation
10-1 sequences series and sigma notation 10-3 geometric sequences and series
10-3 geometric sequences and series Sequence and series formulas pdf
Sequence and series formulas pdf Sequences and series math 20-1
Sequences and series math 20-1 Chapter 1 sequences and series
Chapter 1 sequences and series Sequences and series math 20-1
Sequences and series math 20-1 Sequences and series
Sequences and series Sequences and series math 20-1
Sequences and series math 20-1 Sequences and series games
Sequences and series games Sum formula for arithmetic sequence
Sum formula for arithmetic sequence Sequences and series math 20-1
Sequences and series math 20-1 Sequence and series
Sequence and series The nth term of a geometric sequence has the form
The nth term of a geometric sequence has the form Dr frost sequences
Dr frost sequences Infinite vs finite geometric series
Infinite vs finite geometric series Sum of gp
Sum of gp Formula for infinite geometric series
Formula for infinite geometric series Sum of gp formula
Sum of gp formula L'hopital's rule
L'hopital's rule Ramanujan infinite series
Ramanujan infinite series Arithmetic series formula
Arithmetic series formula Formula of nth term of geometric sequence
Formula of nth term of geometric sequence Sum of infinite arithmetic progression
Sum of infinite arithmetic progression Arithmetic sequence sigma notation
Arithmetic sequence sigma notation Partial sum of arithmetic sequence
Partial sum of arithmetic sequence Series aiding and series opposing
Series aiding and series opposing Maclaurin series vs taylor series
Maclaurin series vs taylor series Heisenberg 1925 paper
Heisenberg 1925 paper Taylor series of composite functions
Taylor series of composite functions Taylor frederick
Taylor frederick Ibm p series
Ibm p series Series-series feedback amplifier
Series-series feedback amplifier Subset text
Subset text Infinite limits and limits at infinity
Infinite limits and limits at infinity Explicet formula
Explicet formula Geometric and arithmetic sequences formulas
Geometric and arithmetic sequences formulas Arithmetic explicit formula
Arithmetic explicit formula Patterns and sequences module 4
Patterns and sequences module 4 Exponential sequence formula
Exponential sequence formula Sequences and sets
Sequences and sets How to calculate nth term
How to calculate nth term Lesson 3: arithmetic and geometric sequences
Lesson 3: arithmetic and geometric sequences Patterns and sequences module quiz b
Patterns and sequences module quiz b How to write a geometric sequence
How to write a geometric sequence Un=u1rn-1
Un=u1rn-1 Arithmetic and geometric sequences formulas
Arithmetic and geometric sequences formulas Icwpcsd
Icwpcsd Uncountable infinity symbol
Uncountable infinity symbol Lyons township grading scale
Lyons township grading scale Bonnie tyler reaching for the infinite heart
Bonnie tyler reaching for the infinite heart Infinite set example
Infinite set example Infinitive vs prepositional phrase
Infinitive vs prepositional phrase Infinite regress
Infinite regress Generalist practice definition
Generalist practice definition Koch snowflake square
Koch snowflake square What is finite loading
What is finite loading Electric field of infinite line
Electric field of infinite line Sheet of charge electric field
Sheet of charge electric field Dimension of a vector space
Dimension of a vector space Proper subset
Proper subset What is a set?
What is a set? Berea infinite campus
Berea infinite campus Oscillating discontinuity definition
Oscillating discontinuity definition What is a infinite set
What is a infinite set Duchamp fountain
Duchamp fountain Management of waiting lines
Management of waiting lines Sigma notation infinite
Sigma notation infinite Sd27j infinite campus
Sd27j infinite campus ออโตมาตา
ออโตมาตา Potential well in quantum mechanics
Potential well in quantum mechanics Infinite potential barrier
Infinite potential barrier Limits at infinity definition
Limits at infinity definition Determine infinite limit
Determine infinite limit Infinite campus pittsford
Infinite campus pittsford Infinite campus pittsford
Infinite campus pittsford Infinite campus mtsd
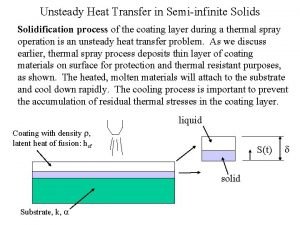
Infinite campus mtsd Semi-infinite solid
Semi-infinite solid Aunt alexandra tries to scold atticus for allowing
Aunt alexandra tries to scold atticus for allowing Machinery
Machinery How to find cardinal number of a set
How to find cardinal number of a set Future perfect and perfect infinitive
Future perfect and perfect infinitive Infinitive phrase?
Infinitive phrase? The infinity concept
The infinity concept Thin lens vergence equation
Thin lens vergence equation Luella high school dress code
Luella high school dress code Infinite data structures
Infinite data structures Tre enti fondamentali della geometria
Tre enti fondamentali della geometria Infinite
Infinite Complicated math
Complicated math Infinite imaging
Infinite imaging Willmar infinite campus
Willmar infinite campus Infinite campus cbsd
Infinite campus cbsd Prairie view high school basketball
Prairie view high school basketball Infinite regress
Infinite regress Infinite campus perth amboy
Infinite campus perth amboy To be present simple
To be present simple Infinite sequence
Infinite sequence Periodic pattern meaning
Periodic pattern meaning Infinite energy center parking
Infinite energy center parking Infinite cardinal
Infinite cardinal What is infinite loop in java
What is infinite loop in java Noun gerund
Noun gerund Law of gearing
Law of gearing Electric field infinite plate
Electric field infinite plate Einstein chaplin frase
Einstein chaplin frase Cusd80 infinite campus
Cusd80 infinite campus Infinite computing
Infinite computing Scos skyward
Scos skyward Imacros infinite loop
Imacros infinite loop Infinite campus coweta
Infinite campus coweta Infinite campus laurel mt
Infinite campus laurel mt Infinite energy incorporated srl
Infinite energy incorporated srl Dvhs infinite campus
Dvhs infinite campus Henry clay high school graduation 2021
Henry clay high school graduation 2021 Enti primitivi
Enti primitivi Rancho pico infinite campus
Rancho pico infinite campus