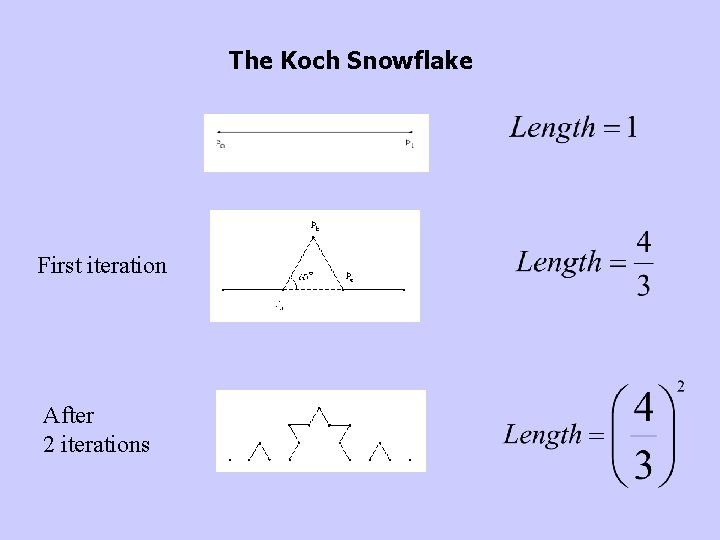
Fractals The Koch Snowflake First iteration After 2











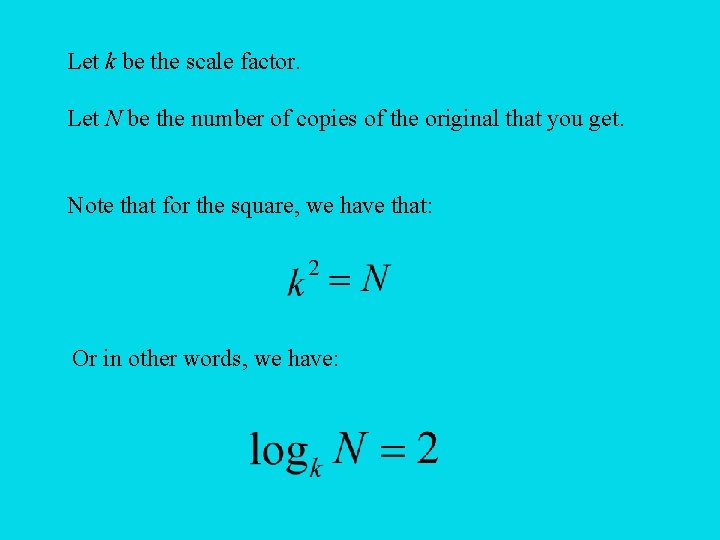
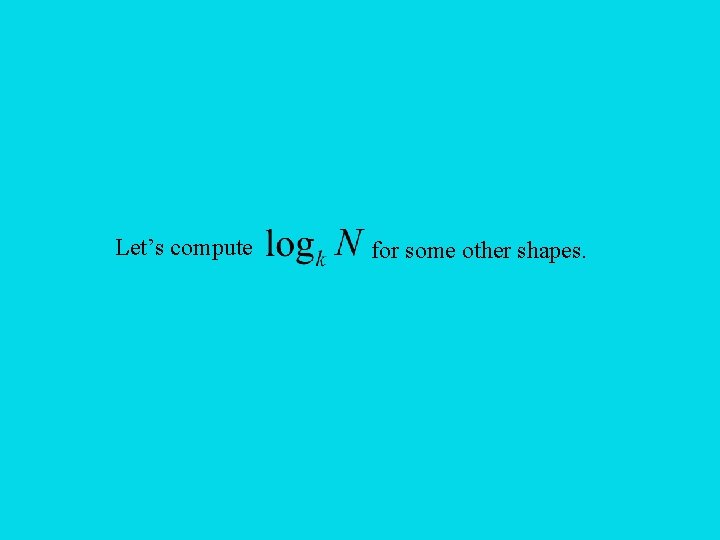




















- Slides: 44

Fractals

The Koch Snowflake First iteration After 2 iterations

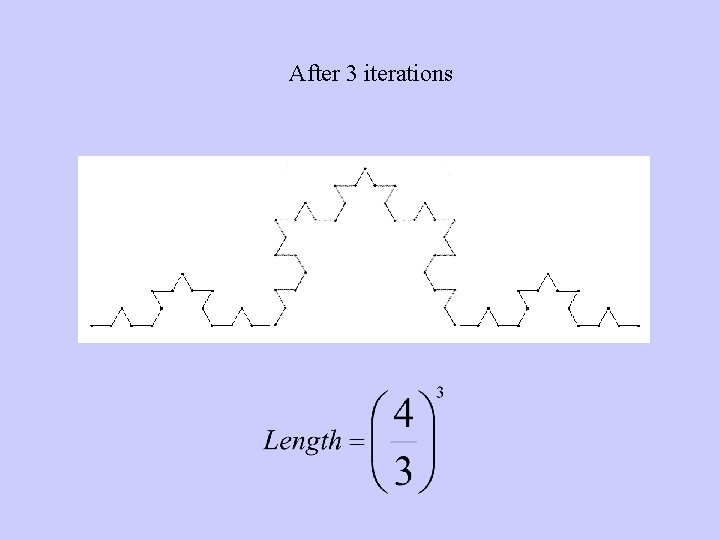
After 3 iterations

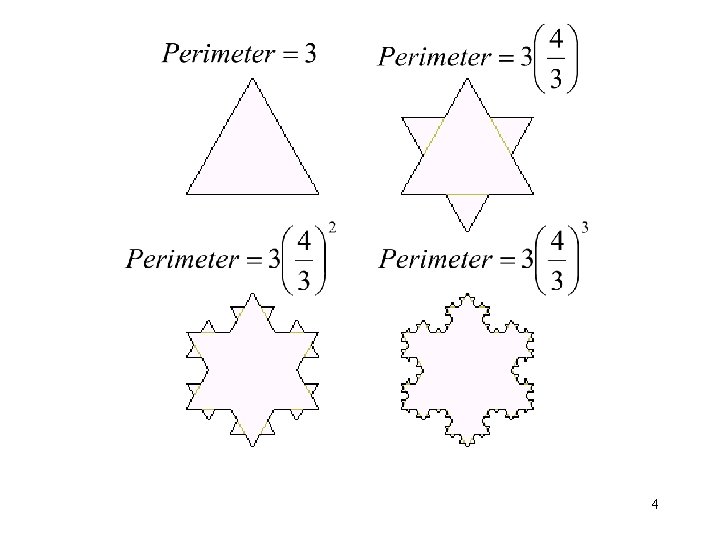
4

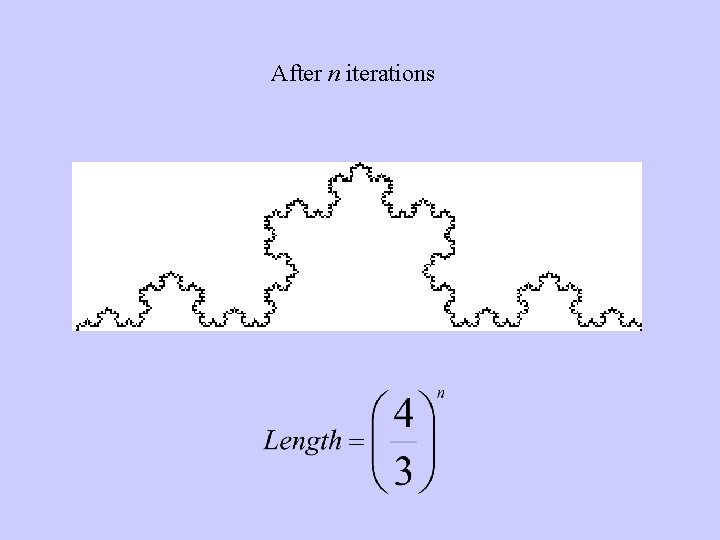
After n iterations

After iterations (work with me here, people)

The Koch snowflake is six of these put together to form. . . well, a snowflake.

Notice that the perimeter of the Koch snowflake is infinite. . . but that the area it bounds is finite (indeed, it is contained in the white square).

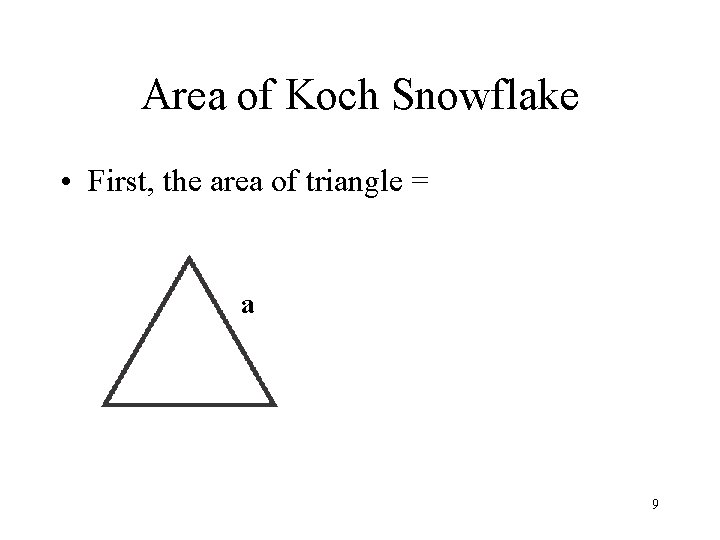
Area of Koch Snowflake • First, the area of triangle = a 9

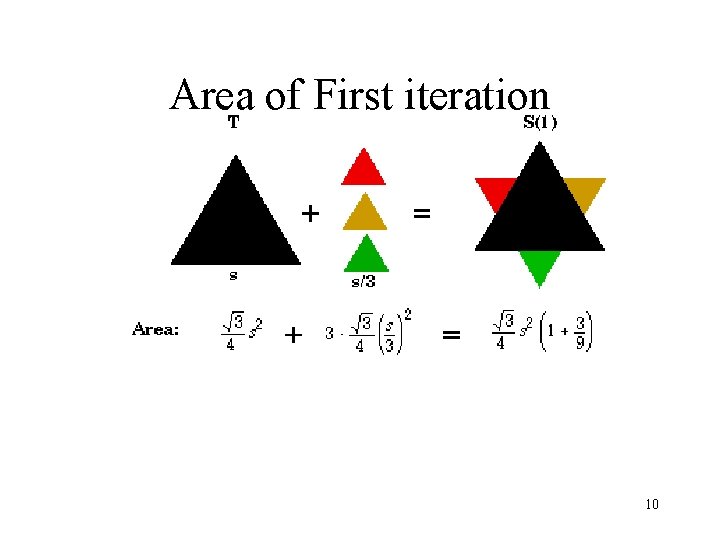
Area of First iteration 10

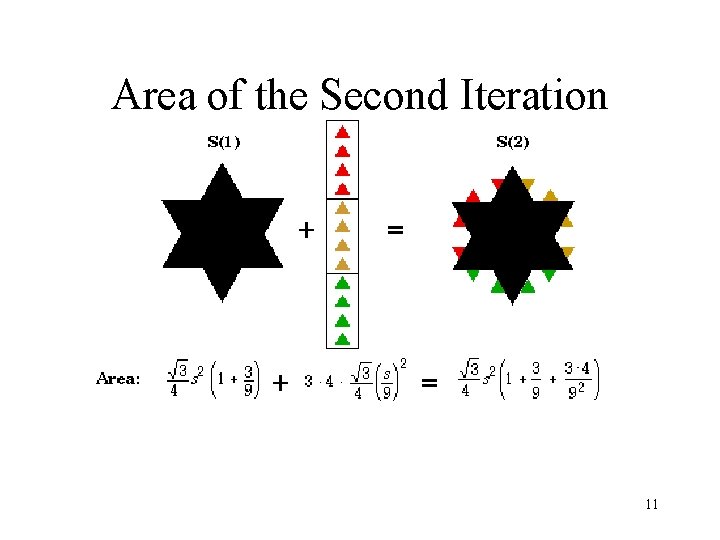
Area of the Second Iteration 11

Area of the Third iteration 12

Formula for area of Koch Snowflake 13


Each of the six sides of the Koch snowflake is self-similar: If you take a small copy of it. . . then dilate by a factor of 3. . . you get four copies of the original.

But self-similarity is not what makes the Koch snowflake a fractal! (Contrary to a common misconception. ) After all, many common geometric objects exhibit self-similarity. Consider, for example, the humble square.

If you take a small square. . . and dilate by a factor of 2. . . then you get 4 copies of the original. A square is self-similar, but it most certainly is not a fractal.

If you take a small square. . . and dilate by a factor of 3. . . then you get 9 copies of the original.
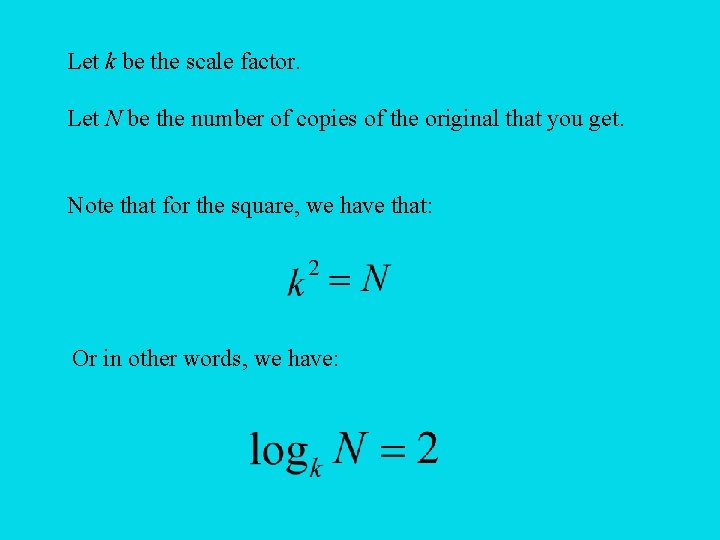
Let k be the scale factor. Let N be the number of copies of the original that you get. Note that for the square, we have that: Or in other words, we have:
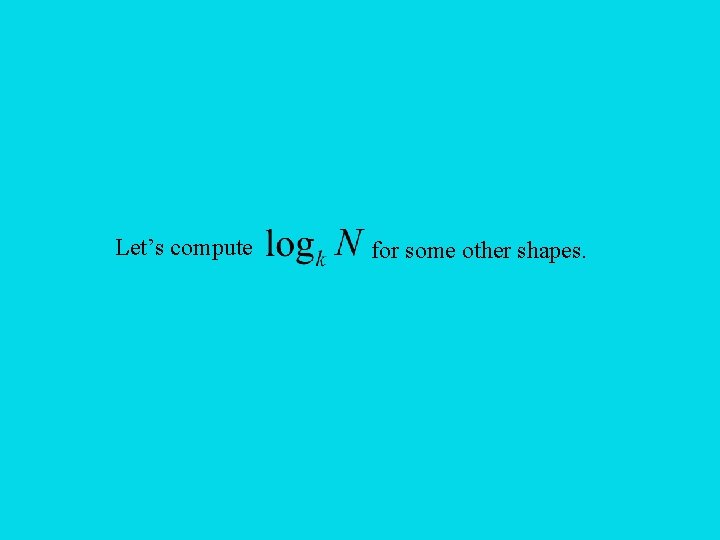
Let’s compute for some other shapes.

Line segment Original Dilated k = scale factor = 2 N = number of copies of original = 2

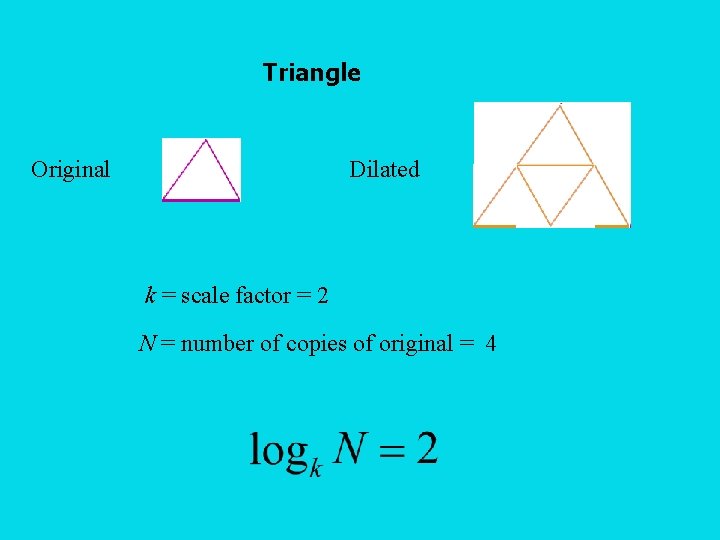
Triangle Original Dilated k = scale factor = 2 N = number of copies of original = 4

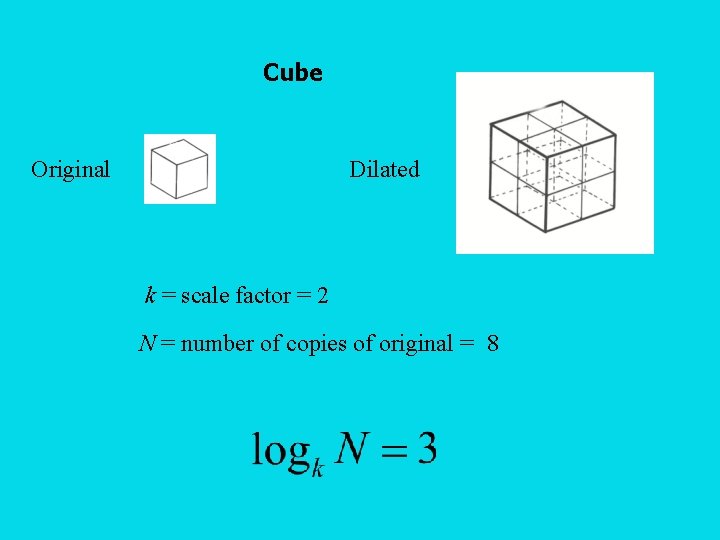
Cube Original Dilated k = scale factor = 2 N = number of copies of original = 8


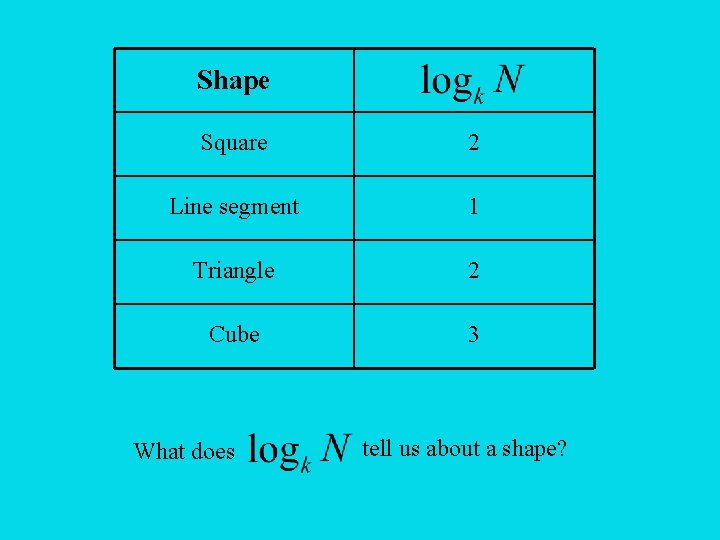
Shape Square 2 Line segment 1 Triangle 2 Cube 3 What does tell us about a shape?

That’s right: tells us the dimension of the shape. (Note that for this to make sense, the shape has to be self-similar. ) So for a self-similar shape, we can take to be the definition of its dimension. (It turns out that this definition coincides with a much more general definition of dimension called the fractal dimension. )
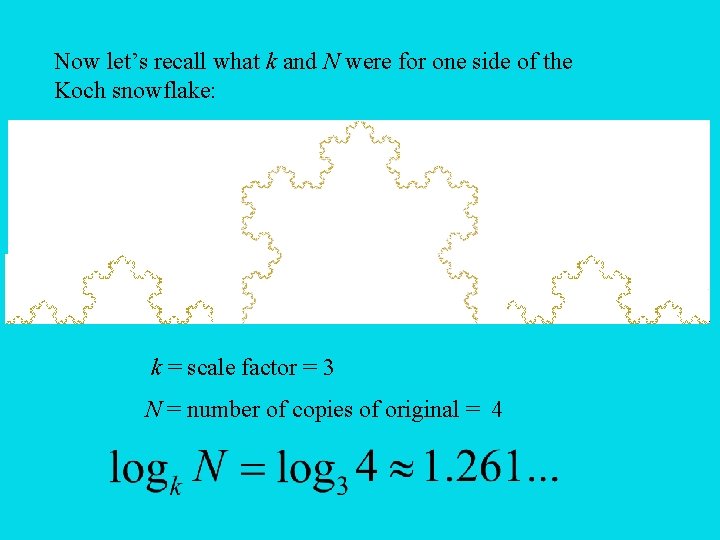
Now let’s recall what k and N were for one side of the Koch snowflake: k = scale factor = 3 N = number of copies of original = 4

So each side of the Koch snowflake is approximately 1. 261 -dimensional. That’s what makes the Koch snowflake a fractal – the fact that its dimension is not an integer. Even shapes which are not self-similar can be fractals. The most famous of these is the Mandelbrot set.

The Sierpinski Carpet

perimeter = 4(3) + 4(1) area = Start with a square of side length 3, with a square of side length 1 removed from its center.

perimeter = area = Think of this shape as consisting of eight small squares, each of side length 1. From each small square, remove its central square.

Iterate.

perimeter = area = Iterate.

perimeter = area = Iterate.

perimeter = area = Iterate.

perimeter = area = Iterate.

The Sierpinski carpet is what’s left after you’re finished removing everything. In other words, it’s the intersection of all the previous sets.

perimeter =

area = =0

So the Sierpinski carpet has an infinite perimeter – but it bounds a region with an area of zero! Weird

Your turn: compute the fractal dimension of the Sierpinski carpet.

The Sierpinski carpet has a 3 -dimensional analogue called the Menger sponge.

Its surface area is infinite, yet it bounds a region of zero volume.

The fractal dimension of the Menger sponge is: