Chapter 2 Introduction to Logic and Sets Copyright

2 -2 Describing Sets Students will be able to understand explain • Set language

Describing Sets In the years from 1871 through 1884, Georg Cantor created set theory

The Language of Sets § A set is any group or collection of objects.

The Language of Sets § Each element of a set is listed only once.

Methods of Describing Sets Listing Method (Roster Method) C = {red, green, yellow, blue}

Methods of Describing Sets Set-Builder Notation the set of all elements x such that

Example Write the following sets using set-builder notation. a. {2, 4, 6, 8, 10,

Example a. Write the set A = {2 k + 1 | k =

Example b. Write the set B = {x|x is a positive even natural number

Definition Two sets are equal if, and only if, they contain the same elements.

Definition One-to-One Correspondence If the elements of sets P and S can be paired

One-to-One Correspondence Set {1, 2, 3} can be placed in a one-to-one correspondence with

One-to-One Correspondence One way to illustrate all possible one-to-one correspondences is to use a

How can we determine the number of one-toone correspondences between two sets? § In

Fundamental Counting Principle If event M can occur in m ways and, after it

Equivalent Sets Two sets A and B are equivalent, written A ~ B, if

Example Let A = {p, q, r, s}, B = {a, b, c}, C

Definition The cardinal number of a set S, denoted n(S), indicates the number of

Finite Sets vs. Infinite Sets A set is finite if its cardinality is zero

Finite Sets vs. Infinite Sets An infinite set is a set that is not

More About Sets The universal set U is defined as that set consisting of

Universal Set Suppose the universal set is defined as: U = {x | x

Universal Set U Copyright © 2016, 2013, 2010 Pearson Education, Inc. Venn Diagram Slide

Universal Set Consider the members of the universal set, U, who are females. Since

Complement of a Set Consider the members of the universal set, U, who are

Definition The complement of a set A, written is the set of all elements

Example a. If U = {a, b, c, d} and B = {c, d},

Example (continued) c. If U = N, E = {2, 4, 6, 8, …},

Definition Set B is a subset of set A, written if and only if

Subset vs. Equality of Sets The definition allows for B to be equal to

Proper Subsets Suppose set B is a subset of set A, and B is

Example Given A = {1, 2, 3, 4, 5}, B = {1, 3}, P

Example (continued) Given A = {1, 2, 3, 4, 5}, B = {1, 3},

Inequalities: An Application of Set Concepts Suppose A and B are finite sets. If

Suppose A and B are infinite sets. Let N = {1, 2, 3, 4,

Number of Subsets of a Finite Set 1. If P = {a}, then P

Slides: 37

Download presentation

2 -2 Describing Sets Students will be able to understand explain • Set language and structure as applied to elementary mathematics. • Connections between finite sets and whole numbers. • Uses of one-to-one correspondence. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 2

Describing Sets In the years from 1871 through 1884, Georg Cantor created set theory which has a profound effect on research and mathematical teaching. Sets, and relations between sets, are a basis for teaching children the concept of a whole number and the concept of “less than” as well as addition, subtraction, and multiplication of whole numbers. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 3

The Language of Sets § A set is any group or collection of objects. § The objects that belong to a set are the elements, or members, of the set. § One method of denoting a set is to simply list the elements inside braces and label the set with a capital letter. A = {1, 2, 3, 4, 5} Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 4

The Language of Sets § Each element of a set is listed only once. § The order of the elements is unimportant. § We symbolize that an element belongs to a set using the symbol , and we use to indicate that an element does not belong to a set. § A set must be well-defined. We must be able to tell whether or not an object belongs to the set. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 5

Methods of Describing Sets Listing Method (Roster Method) C = {red, green, yellow, blue} N = {1, 2, 3, 4, … } natural numbers Ellipsis – continues in the same manner L = {a, b, c, d, …} lower case letters Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 6

Methods of Describing Sets Set-Builder Notation the set of all elements x such that x is an element of the set of natural numbers Copyright © 2016, 2013, 2010 Pearson Education, Inc. and x is less than 11 Slide 7

Example Write the following sets using set-builder notation. a. {2, 4, 6, 8, 10, …} b. {1, 3, 5, 7, …} a. {x | x is an even natural number} or {x | x = 2 n, n N} b. {x | x is an odd natural number} or {x | x = 2 n − 1, n N} Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 8

Definition Two sets are equal if, and only if, they contain the same elements. § The order of the elements makes no difference. § If set A is equal to set B, we write A = B. § If A = B, then every element of set A is contained in set B, and every element of set B is contained in set A. § If A ≠ B , then there is at least one element that is not contained in both sets A and B. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 11

Definition One-to-One Correspondence If the elements of sets P and S can be paired so that for each element of P there is exactly one element of S and for each element of S there is exactly one element of P, then the two sets P and S are said to be in a one-to-one correspondence. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 12

One-to-One Correspondence Set {1, 2, 3} can be placed in a one-to-one correspondence with set {a, b, c} by establishing either of the following pairings: These are not the only possible pairs to establish a one-to-one correspondence. We would like to list all the possibilities. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 13

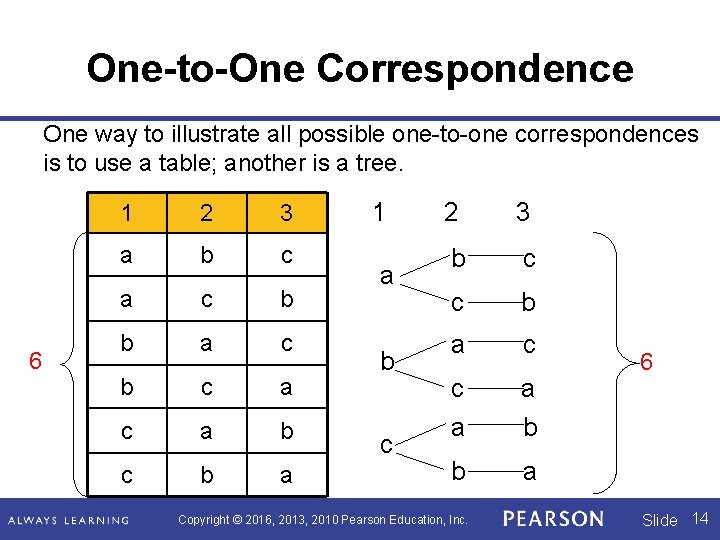
One-to-One Correspondence One way to illustrate all possible one-to-one correspondences is to use a table; another is a tree. 6 1 2 3 a b c a c b b a c b c a b c b a 1 a b c 2 3 b c c b a c c a a b b a Copyright © 2016, 2013, 2010 Pearson Education, Inc. 6 Slide 14

How can we determine the number of one-toone correspondences between two sets? § In our example, given the element 1 in the first set, there are three possible elements in the second set which can be paired with the 1, namely a, b, or c. § Once we have paired an element with 1, that leaves two elements in the second set to pair with the number 2. § Once we have paired an element in the second set with 1 and with 2, there will be one element left in the second set to pair with 3. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 15

Fundamental Counting Principle If event M can occur in m ways and, after it has occurred, event N can occur in n ways, then event M followed by event N can occur in m • n ways. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 16

Equivalent Sets Two sets A and B are equivalent, written A ~ B, if there exists a one-to-one correspondence between the sets. § Recall if two sets are equal, they have the same elements. § Equal sets are equivalent, but equivalent sets are not necessarily equal. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 17

Example Let A = {p, q, r, s}, B = {a, b, c}, C = {x, y, z}, and D = {b, a, c}. Compare the sets, using the terms equal and equivalent. Each set is both equivalent and equal to itself. Sets A and B are not equivalent and not equal. Sets A and C are not equivalent and not equal. Sets A and D are not equivalent and not equal. Sets B and C are equivalent but not equal. Sets B and D are equivalent and equal. Sets C and D are equivalent but not equal. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 18

Definition The cardinal number of a set S, denoted n(S), indicates the number of elements in the set S. What is the cardinality of each of the following? K = {3, 5, 8, 0, 11} n(K) = 5 L = {0} n(L) = 1 X = {x | x is a real number and x = x + 1} n(X) = 0 Y=Ø n(Y) = 0 Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 19

Finite Sets vs. Infinite Sets A set is finite if its cardinality is zero or a natural number. Examples The set of presidents of the United States. n(P) = 45 The set of planets in our solar system. n(P) = ____ Then, name all 9 of the planets. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 20

Finite Sets vs. Infinite Sets An infinite set is a set that is not finite. Examples The set of whole numbers = { 0, 1, 2, 3, …}. The set of solutions to the equation x + 1 = x + 1. This equation works for all real numbers. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 21

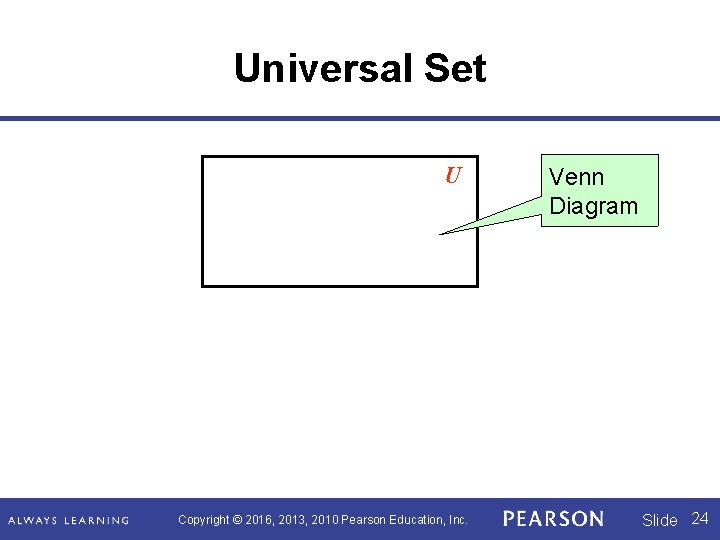
More About Sets The universal set U is defined as that set consisting of all elements under consideration. We usually denote the universal set with a capital U. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 22

Universal Set Suppose the universal set is defined as: U = {x | x is a member of the U. S. Senate} n(U) = 2 per state × 50 states = _____ Denote the universal set with a large rectangle, and particular sets are indicated by geometric figures inside the rectangle. In this case, only members of the U. S. Senate are included in the rectangle. This pictorial representation is a Venn diagram. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 23

Universal Set Consider the members of the universal set, U, who are females. Since this set is wholly contained in U but does not contain all the members of U, we denote this set with a circle as follows: F = {x | x is a female U. S. senator} U F Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 25

Complement of a Set Consider the members of the universal set, U, who are not females. This is the set of all members of the set, U, that are not in set F. We refer to this set as the complement of set F and denote it by the shaded region in the figure below. F = {x | x is a female U. S. senator} U F Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 26

Example a. If U = {a, b, c, d} and B = {c, d}, find b. If U = {x | x is an animal in the zoo} and S = {x | x is a snake in the zoo}, describe = {x | x is a zoo animal that is not a snake} Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 28

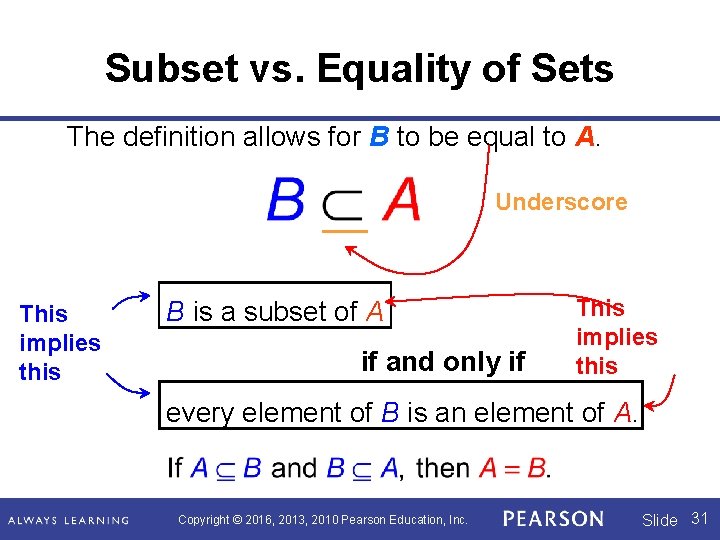
Definition Set B is a subset of set A, written if and only if every element of B is an element of A. When a set A is not a subset of another set B, we write Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 30

Subset vs. Equality of Sets The definition allows for B to be equal to A. Underscore This implies this B is a subset of A if and only if This implies this every element of B is an element of A. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 31

Proper Subsets Suppose set B is a subset of set A, and B is not equal to A. A U B Then there must be at least one element of A that is not in B. We say that B is a proper subset of A, written Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 32

Example Given A = {1, 2, 3, 4, 5}, B = {1, 3}, P = {x | x = 2 n − 1, where n N}. a. Identify all the subset relationships that occur among these sets. Because 21 − 1 = 1, 22 − 1 = 3, 23 − 1 = 7, 24 − 1 = 15, and so on, P = {1, 3, 7, 15, …}. So, Also Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 33

Example (continued) Given A = {1, 2, 3, 4, 5}, B = {1, 3}, P = {x | x = 2 n − 1, where n N}. b. Identify all the proper subset relatiohships that occur among these sets. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 34

Inequalities: An Application of Set Concepts Suppose A and B are finite sets. If A = B, then n(A) = n(B), and A and B are equivalent. It is possible to establish a one-to-one correspondence between A and B. If A is a proper subset of B, then n(A) < n(B), and it is not possible to establish a one-to-one correspondence between A and B. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 35

Suppose A and B are infinite sets. Let N = {1, 2, 3, 4, 5, …, n, …} and W = {0, 1, 2, 3, 4, …, n – 1, n, …}. Clearly, N W. But it is still possible to establish a one-toone correspondence between the sets by letting each element in N correspond to a number in W that is one smaller. Thus, N ~ W. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 36

Number of Subsets of a Finite Set 1. If P = {a}, then P has two subsets, Ø and {a}. 2. If Q = {a, b}, then Q has four subsets, Ø, {a}, {b}, and {a, b}. 3. If R = {a, b, c}, then R has eight subsets, Ø, {a}, {b}, {c}, {a, b}, {a, c}, {b, c} and {a, b, c}. In general, if there are n elements in a set, then 2 n subsets can be formed. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 37