Why Study Solid State Physics Ideal Crystal An
















































- Slides: 71

Why Study Solid State Physics?

Ideal Crystal • An ideal crystal is a periodic array of structural units, such as atoms or molecules. • It can be constructed by the infinite repetition of these identical structural units in space. • Structure can be described in terms of a lattice, with a group of atoms attached to each lattice point. The group of atoms is the basis.

Bravais Lattice • An infinite array of discrete points with an arrangement and orientation that appears exactly the same, from any of the points the array is viewed from. • A three dimensional Bravais lattice consists of all points with position vectors R that can be written as a linear combination of primitive vectors. The expansion coefficients must be integers.

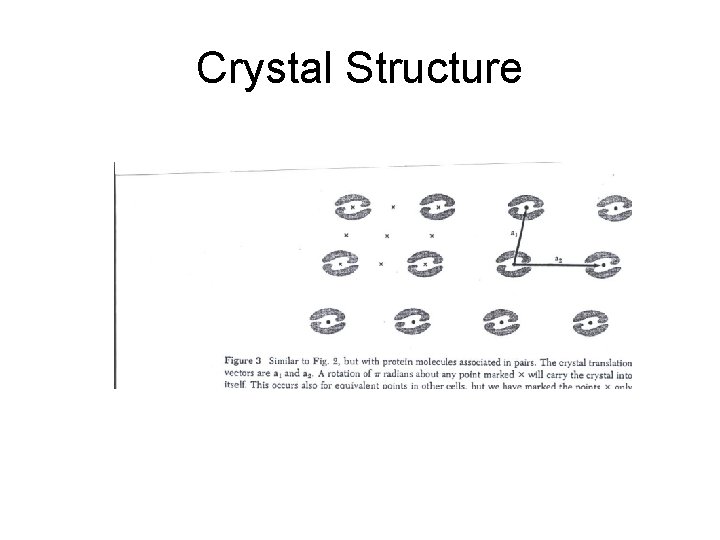
Crystal lattice: Proteins

Crystal Structure

Honeycomb: NOT Bravais

Honeycomb net: Bravais lattice with two point basis

Crystal structure: basis

Translation Vector T

Translation(a 1, a 2), Nontranslation Vectors(a 1’’’, a 2’’’)

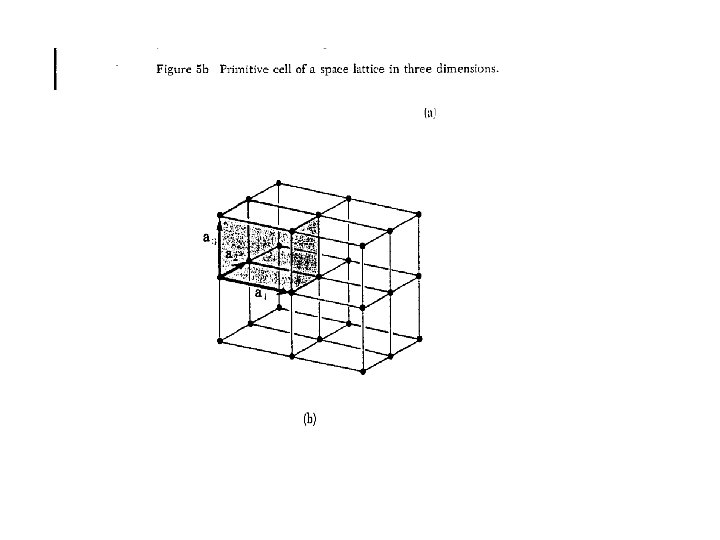
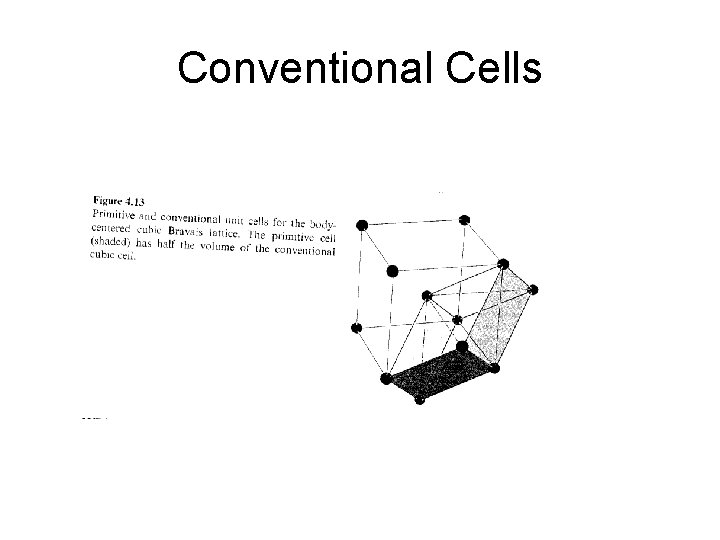
Primitive Unit Cell • A primitive cell or primitive unit cell is a volume of space that when translated through all the vectors in a Bravais lattice just fills all of space without either overlapping itself or leaving voids. • A primitive cell must contain precisely one lattice point.


Fundamental Types of Lattices • Crystal lattices can be mapped into themselves by the lattice translations T and by various other symmetry operations. • A typical symmetry operation is that of rotation about an axis that passes through a lattice point. Allowed rotations of : 2 π, 2π/2, 2π/3, 2π/4, 2π/6 • (Note: lattices do not have rotation axes for 1/5, 1/7 …) times 2π

Five fold axis of symmetry cannot exist

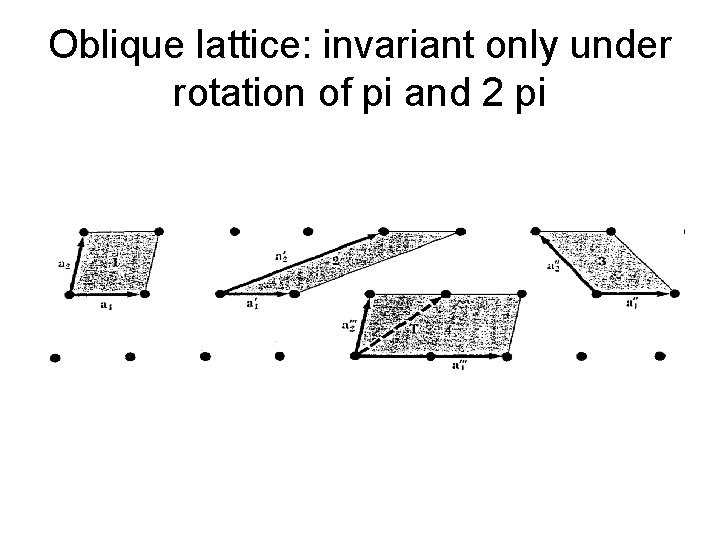
Two Dimensional Lattices • There is an unlimited number of possible lattices, since there is no restriction on the lengths of the lattice translation vectors or on the angle between them. An oblique lattice has arbitrary a 1 and a 2 and is invariant only under rotation of π and 2 π about any lattice point.

Oblique lattice: invariant only under rotation of pi and 2 pi

Two Dimensional Lattices

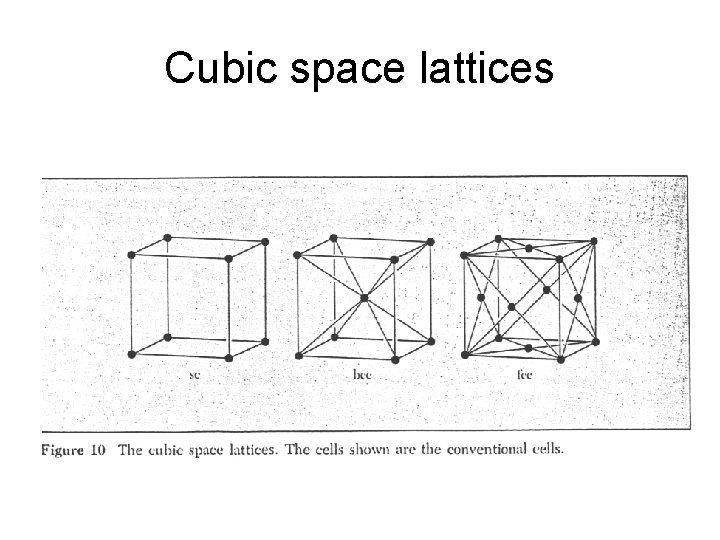
Three Dimensional Lattice Types

Wigner-Seitz Primitive Cell: Full symmetry of Bravais Lattice

Conventional Cells

Cubic space lattices

Cubic lattices

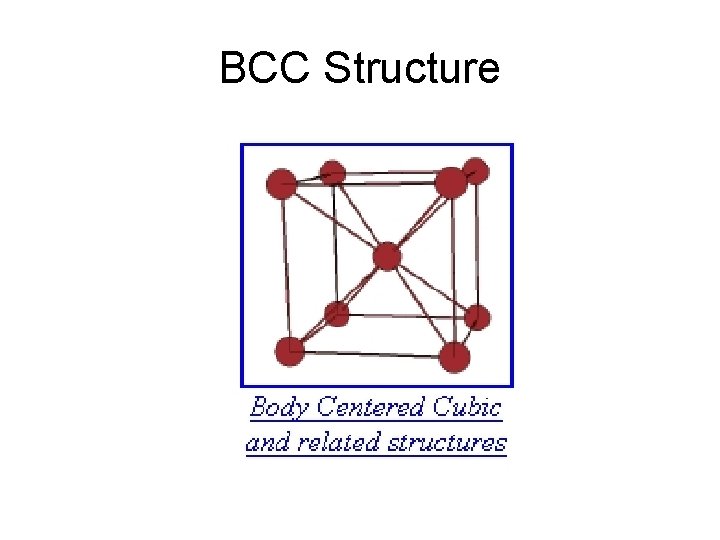
BCC Structure

BCC Crystal

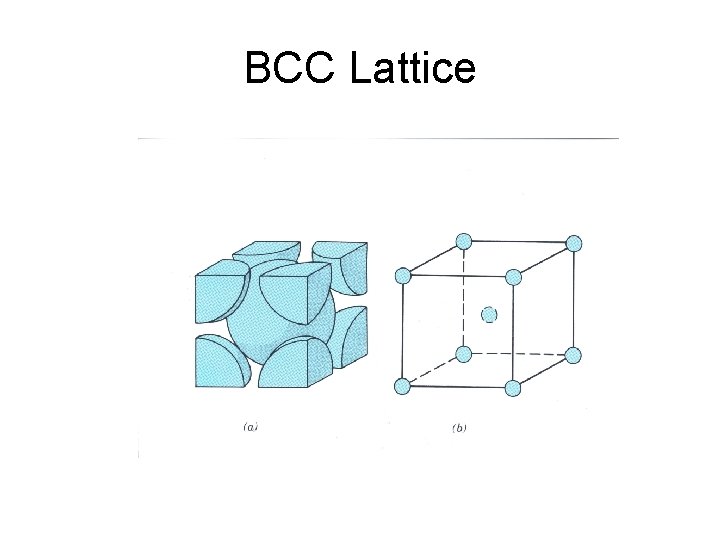
BCC Lattice

Primitive vectors BCC

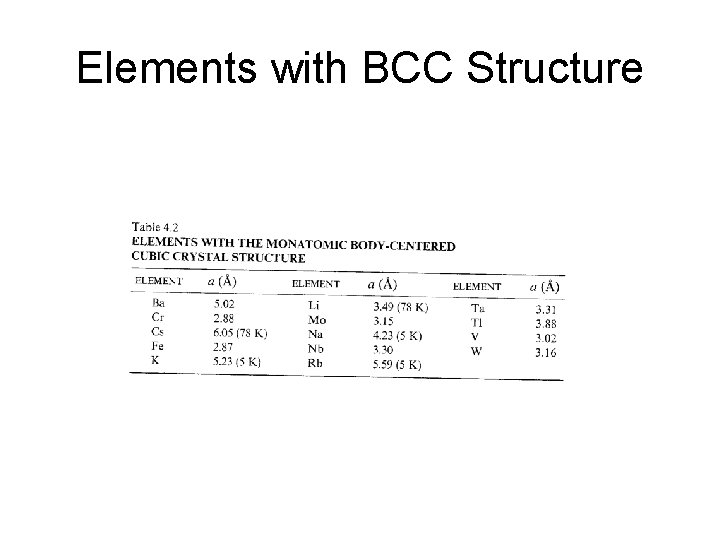
Elements with BCC Structure

Summary: Bravais Lattices (Nets) in Two Dimensions

Escher loved two dimensional structures too

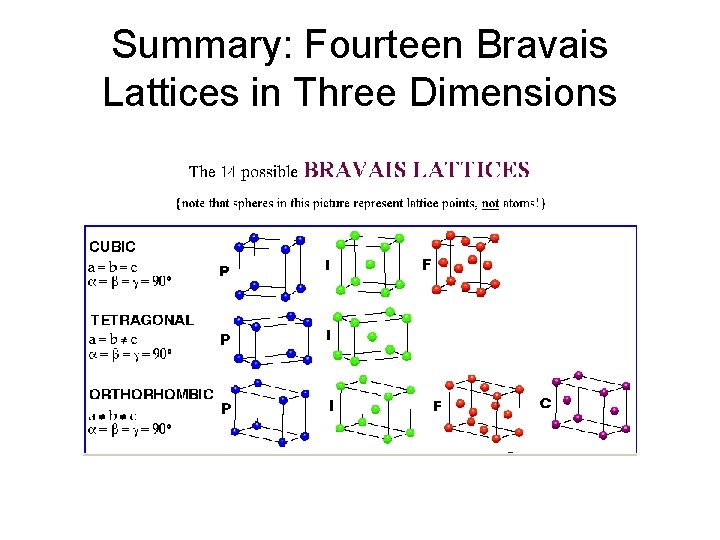
Summary: Fourteen Bravais Lattices in Three Dimensions

Fourteen Bravais Lattices …

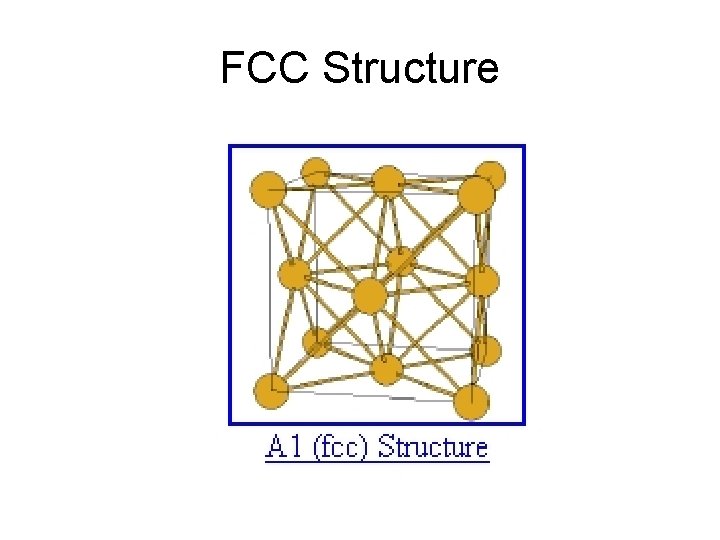
FCC Structure

FCC lattice

Primitive Cell: FCC Lattice

FCC: Conventional Cell With Basis • We can also view the FCC lattice in terms of a conventional unit cell with a four point basis. • Similarly, we can view the BCC lattice in terms of a conventional unit cell with a two point basis.

Elements That Have FCC Structure

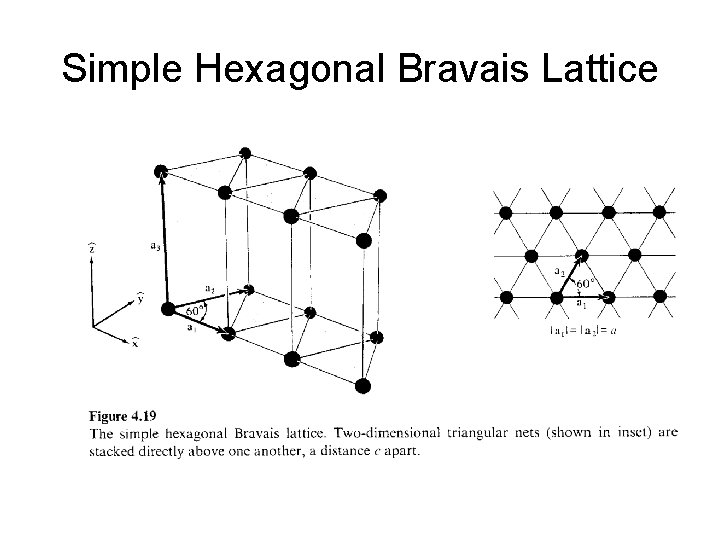
Simple Hexagonal Bravais Lattice

Primitive Cell: Hexagonal System

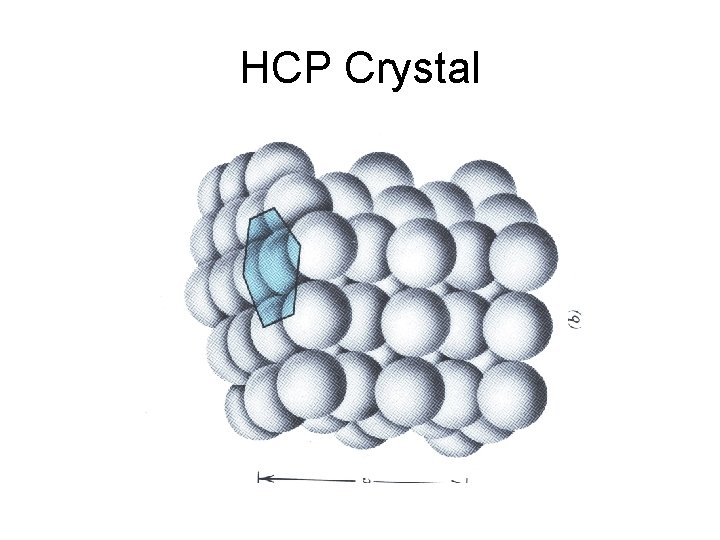
HCP Crystal

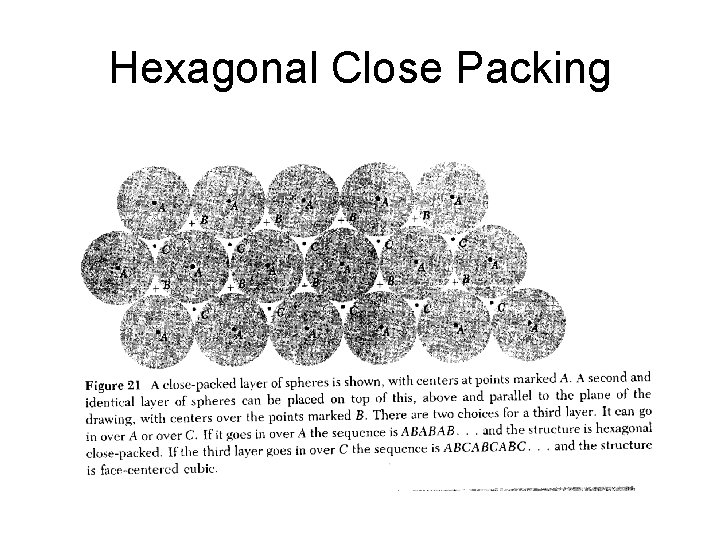
Hexagonal Close Packing

Hexagonal. Close. Packed HCP lattice is not a Bravais lattice, because orientation of the environment Of a point varies from layer to layer along the c-axis.

HCP: Simple Hexagonal Bravais With Basis of Two Atoms Per Point

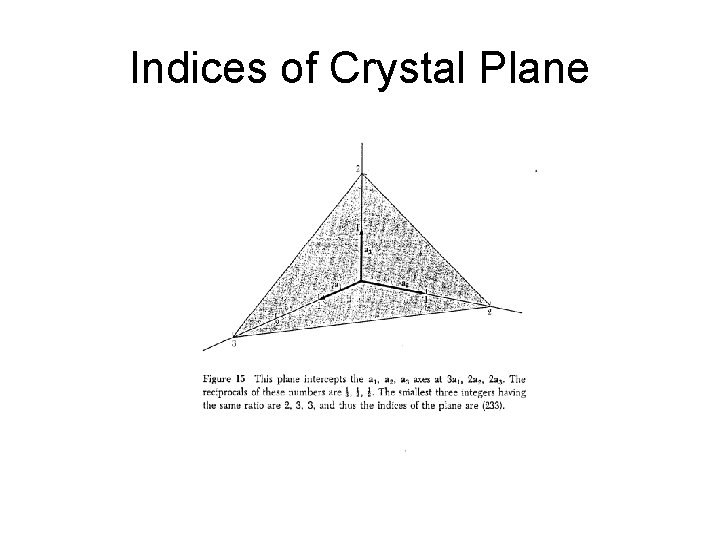
Miller indices of lattice plane • The indices of a crystal plane (h, k, l) are defined to be a set of integers with no common factors, inversely proportional to the intercepts of the crystal plane along the crystal axes:

Indices of Crystal Plane

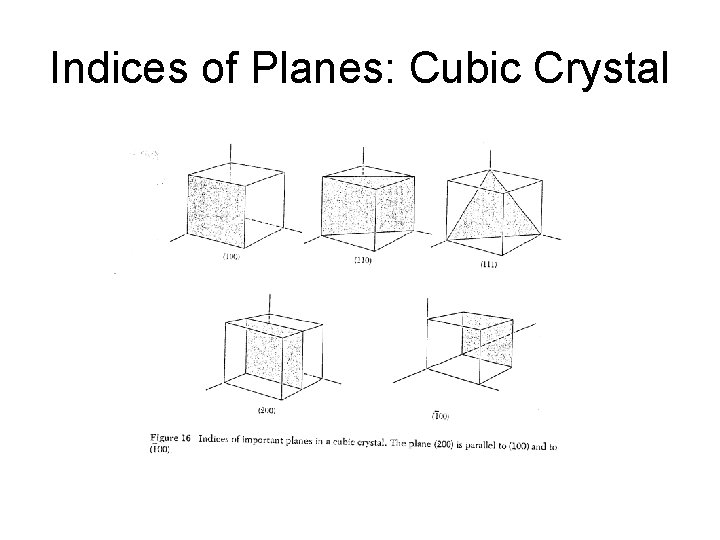
Indices of Planes: Cubic Crystal

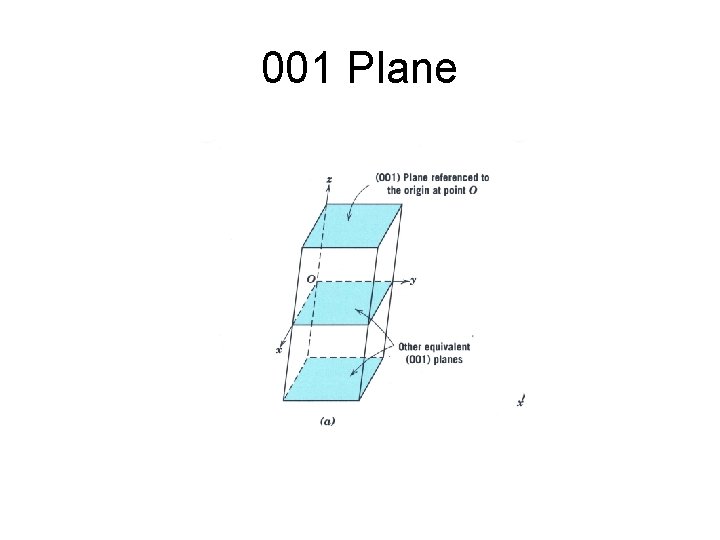
001 Plane

110 Planes

111 Planes

Simple Crystal Structures • There are several crystal structures of common interest: sodium chloride, cesium chloride, hexagonal close-packed, diamond and cubic zinc sulfide. • Each of these structures have many different realizations.

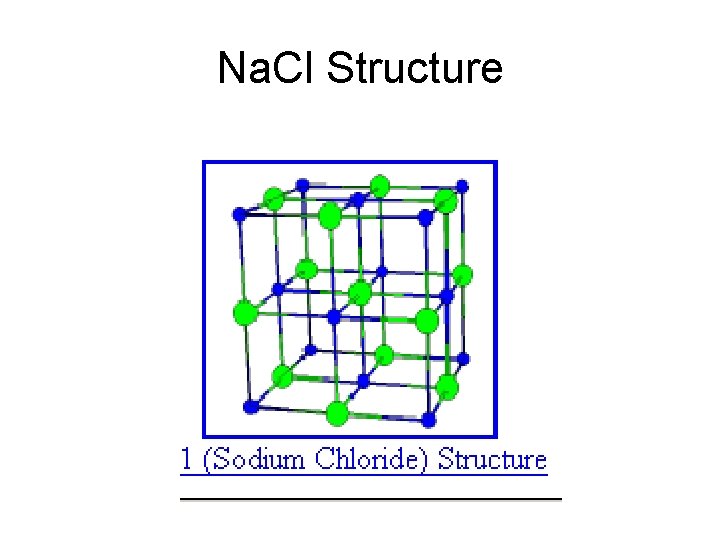
Na. Cl Structure

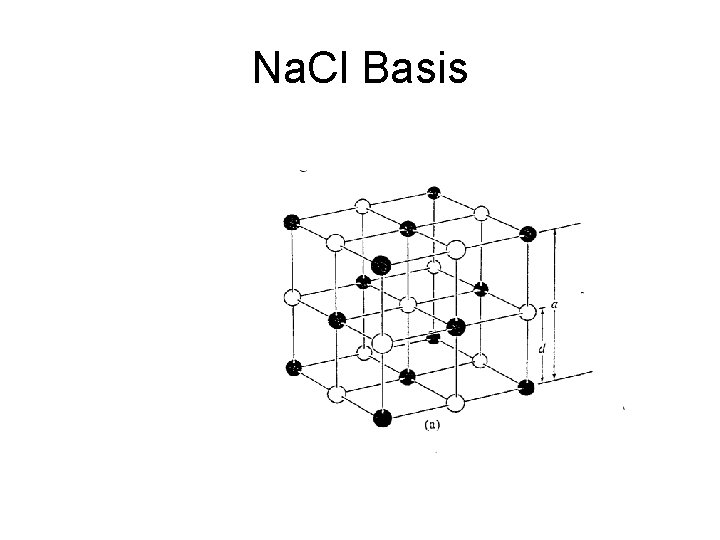
Na. Cl Basis

Na. Cl Type Elements

Cs. Cl Structure

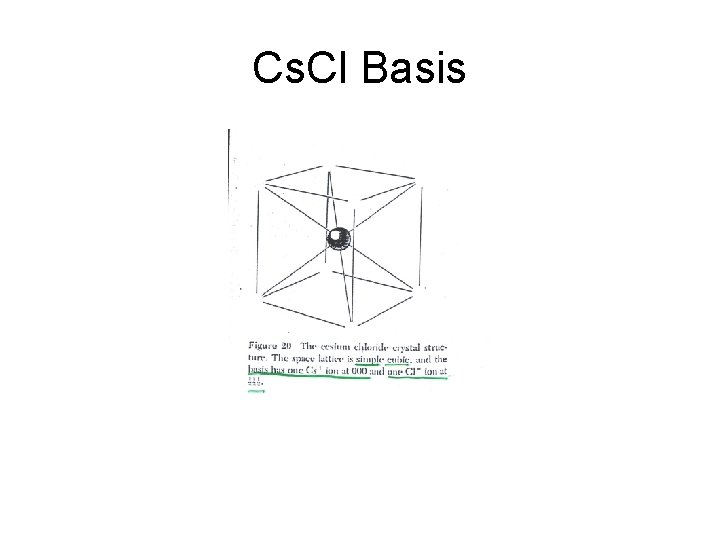
Cs. Cl Basis

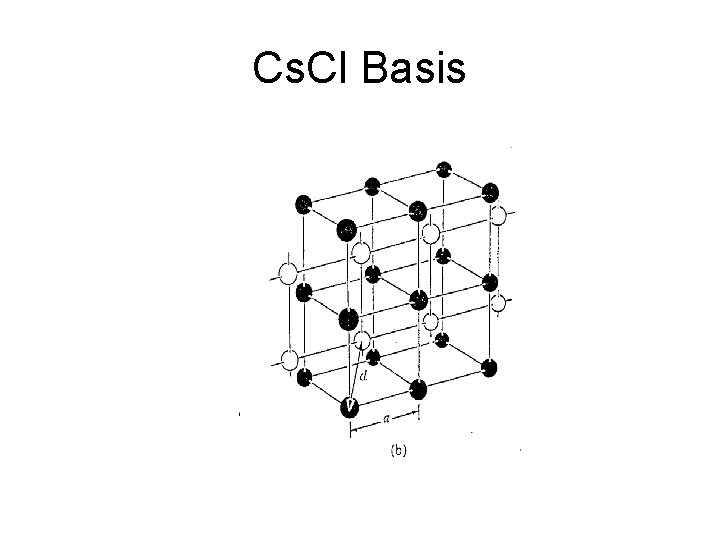
Cs. Cl Basis

Ce. Cl Crystals

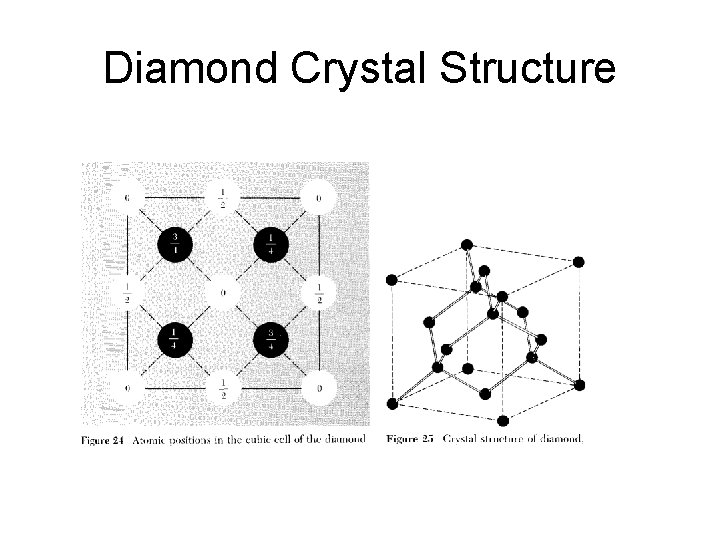
Diamond Crystal Structure

Zinc. Blende structure

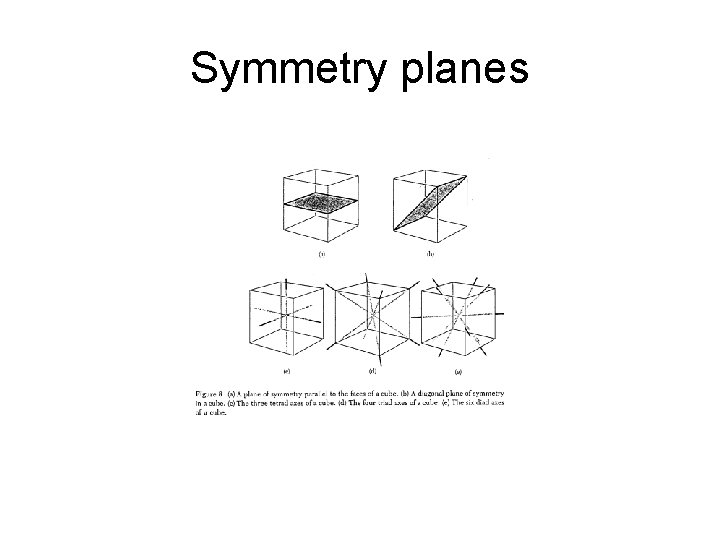
Symmetry planes

The End: Chapter 1


Bravais Lattice: Two Definitions The expansion coefficients n 1, n 2, n 3 must be integers. The vectors a 1, a 2, a 3 are primitive vectors and span the lattice.

HCP Close Packing

HCP Close Packing

Close Packing 2

Close Packing 3

Close Packing 4

Close Packing 5

Na. Cl Basis

Close Packing of Spheres

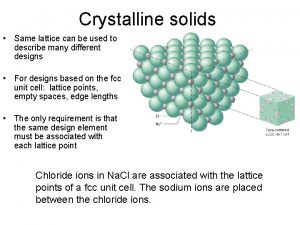
 Crystalline solid
Crystalline solid Pictures
Pictures Define solid state physics
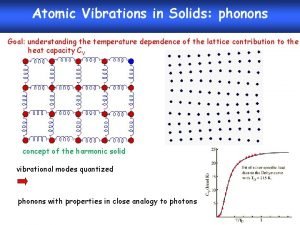
Define solid state physics Magnetism in solid state physics
Magnetism in solid state physics Philip hofmann solid state physics
Philip hofmann solid state physics Philip hofmann solid state physics
Philip hofmann solid state physics Scope of solid state physics
Scope of solid state physics Polycrystalline solids
Polycrystalline solids Solid state physics
Solid state physics Solid state physics
Solid state physics Drude model solid state physics
Drude model solid state physics Solid state physics
Solid state physics Physics
Physics Simulations for solid state physics
Simulations for solid state physics Understanding solid state physics
Understanding solid state physics Philip hofmann solid state physics
Philip hofmann solid state physics Nonliving solid with crystal like properties
Nonliving solid with crystal like properties Structure of nacl
Structure of nacl Crystal state
Crystal state Amorphous vs crystalline
Amorphous vs crystalline Sample of solution
Sample of solution Covalent molecular and covalent network
Covalent molecular and covalent network Crystalline vs non crystalline
Crystalline vs non crystalline Crystalline solid and amorphous solid
Crystalline solid and amorphous solid Anisotropic meaning in chemistry
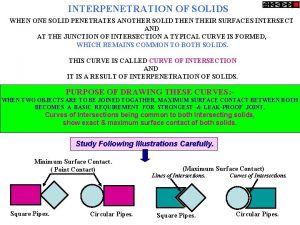
Anisotropic meaning in chemistry When a solid completely penetrates another solid
When a solid completely penetrates another solid When a solid completely penetrates another solid
When a solid completely penetrates another solid Sifting mixture
Sifting mixture Dont ask why why why
Dont ask why why why Partial vapour pressure
Partial vapour pressure From solid state to biophysics
From solid state to biophysics Difference between submerged and solid state fermentation
Difference between submerged and solid state fermentation Solid state rectifier circuit diagram
Solid state rectifier circuit diagram Solid state electronic devices 7th solution chapter 4
Solid state electronic devices 7th solution chapter 4 Te has preguntado alguna vez quién eres tu
Te has preguntado alguna vez quién eres tu Characteristics of solid state
Characteristics of solid state Solid state reduction powder metallurgy
Solid state reduction powder metallurgy Solid state electronic devices ppt
Solid state electronic devices ppt Passive diathermy electrode
Passive diathermy electrode Solid state diode definition
Solid state diode definition Solid state marx generator
Solid state marx generator 4 quadrant operation of induction motor
4 quadrant operation of induction motor Solid state power amplifier definition
Solid state power amplifier definition Ruhestromrelais
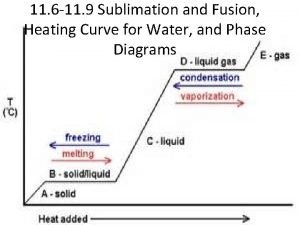
Ruhestromrelais Sublimation fusion
Sublimation fusion Solid state power amplifier definition
Solid state power amplifier definition Solid state recorder side car asic
Solid state recorder side car asic Msc ssl
Msc ssl Solid state welding wikipedia
Solid state welding wikipedia Why does it happen
Why does it happen University physics with modern physics fifteenth edition
University physics with modern physics fifteenth edition Hl physics ia ideas
Hl physics ia ideas Ideal gas equation
Ideal gas equation R constant ideal gas law
R constant ideal gas law Emf equation of transformer
Emf equation of transformer Why are gases easy to compress?
Why are gases easy to compress? Why is heat energy needed to melt a solid
Why is heat energy needed to melt a solid Vce physics study design
Vce physics study design Physics chapter 21 study guide answers
Physics chapter 21 study guide answers Chapter 7 study guide physics
Chapter 7 study guide physics Chapter 11 energy and its conservation answers
Chapter 11 energy and its conservation answers Physics semester 1 final exam study guide answers
Physics semester 1 final exam study guide answers Chapter 4 assessment physics
Chapter 4 assessment physics Webassign ttu
Webassign ttu Representing motion physics answers chapter 2
Representing motion physics answers chapter 2 Physics study group
Physics study group Vce physics practical investigation ideas
Vce physics practical investigation ideas State hooke's law in physics
State hooke's law in physics Igcse hooke's law
Igcse hooke's law Michigan state physics
Michigan state physics Hooke's law statement
Hooke's law statement Hooke's law
Hooke's law