Crystal physics Crystal physics Materials differ from one

Crystal physics

Crystal physics • Materials differ from one another in their properties • The behaviour of material are closely related to their crystal structure. Material Crystalline Non- crystalline or amorphous

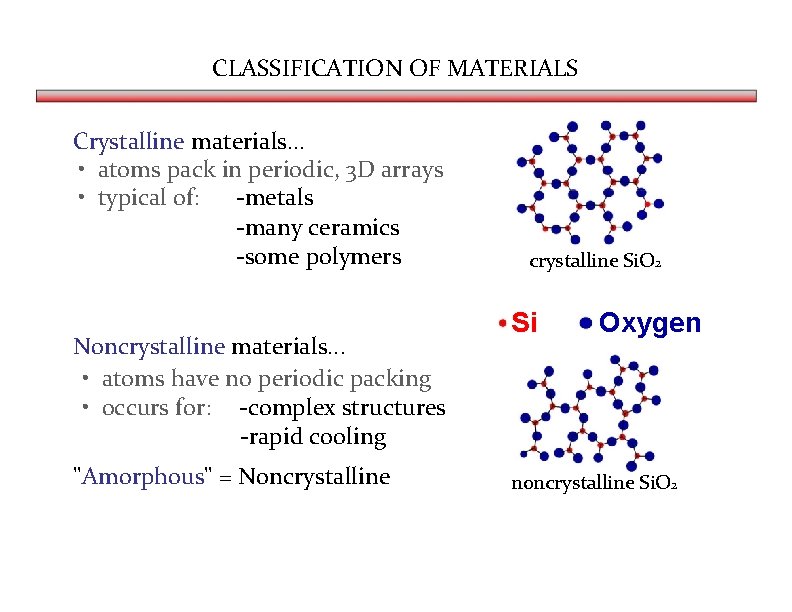
CLASSIFICATION OF MATERIALS Crystalline materials. . . • atoms pack in periodic, 3 D arrays • typical of: -metals -many ceramics -some polymers Noncrystalline materials. . . • atoms have no periodic packing • occurs for: -complex structures -rapid cooling "Amorphous" = Noncrystalline Si. O 2 Si Oxygen noncrystalline Si. O 2

Important Crystalline material - Atoms are arranged in systematic or regular pattern Non-crystalline material - Atoms are arranged randomly Crystal- 3 D solid which consists of periodic arrangement of atoms Crystal structure - The arrangement of atoms in crystal Space lattice - The representation of atoms in the crystal in 3 D is known as space lattice. Defined as It is an array of point in space such that each point in space has an identical sorroundings to that of every other point in array.

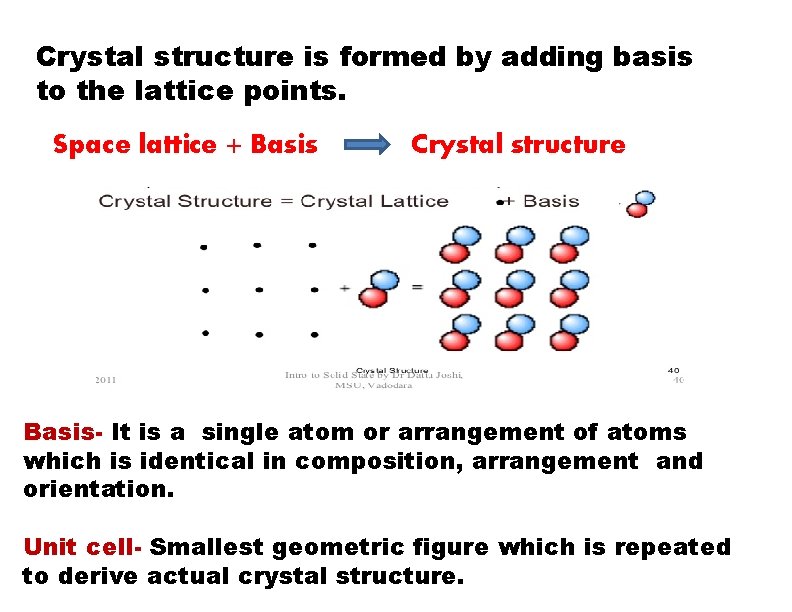
Crystal structure is formed by adding basis to the lattice points. Space lattice + Basis Crystal structure Basis- It is a single atom or arrangement of atoms which is identical in composition, arrangement and orientation. Unit cell- Smallest geometric figure which is repeated to derive actual crystal structure.

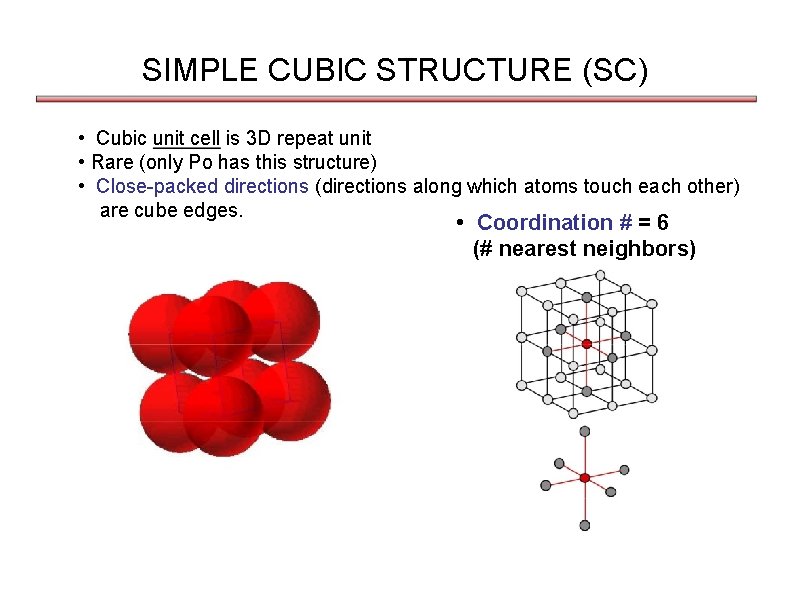
SIMPLE CUBIC STRUCTURE (SC) • Cubic unit cell is 3 D repeat unit • Rare (only Po has this structure) • Close-packed directions (directions along which atoms touch each other) are cube edges. • Coordination # = 6 (# nearest neighbors)

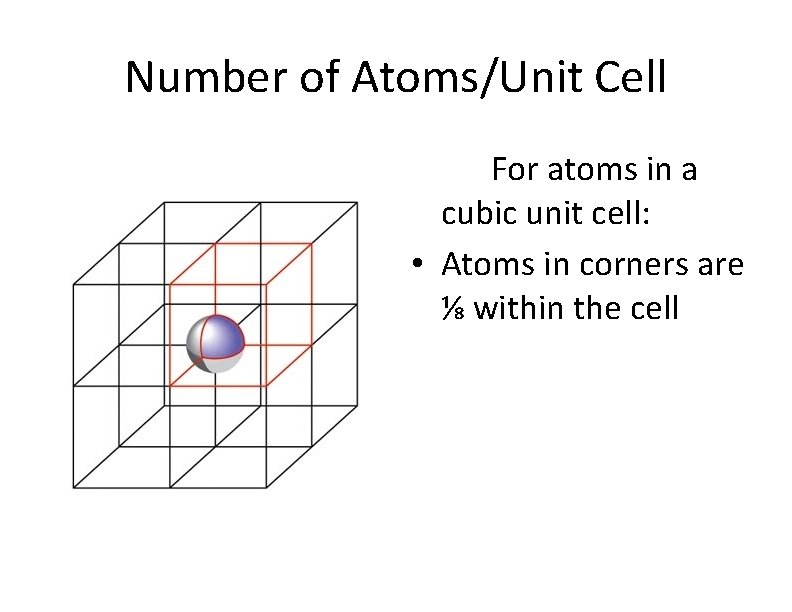
Number of Atoms/Unit Cell For atoms in a cubic unit cell: • Atoms in corners are ⅛ within the cell

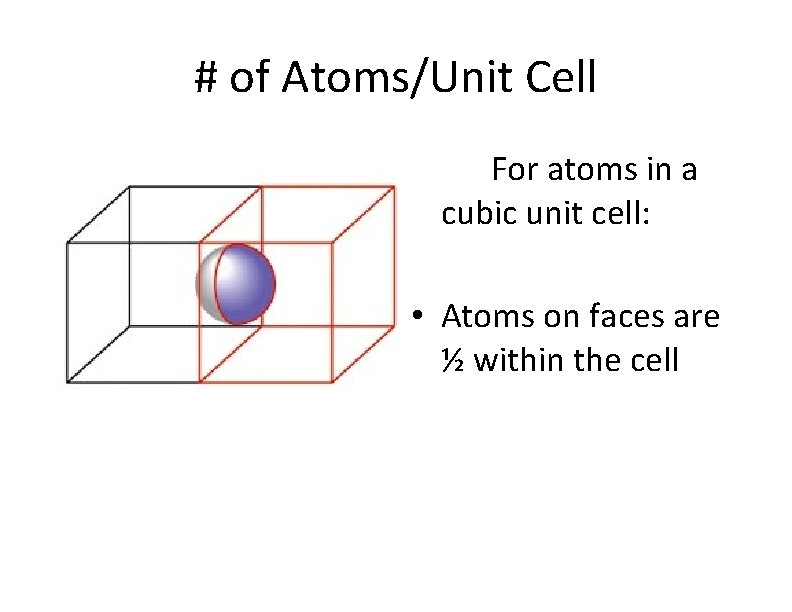
# of Atoms/Unit Cell For atoms in a cubic unit cell: • Atoms on faces are ½ within the cell

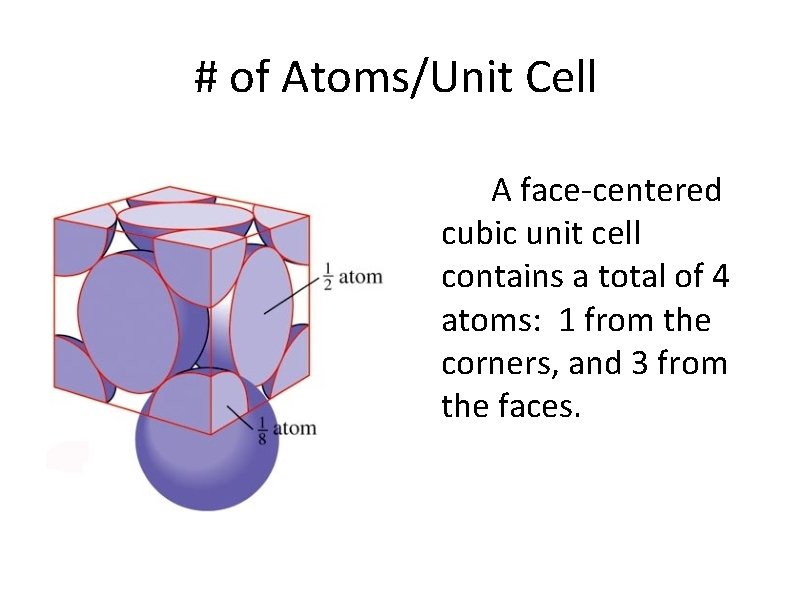
# of Atoms/Unit Cell A face-centered cubic unit cell contains a total of 4 atoms: 1 from the corners, and 3 from the faces.

# of Atoms/Unit Cell For atoms in a cubic unit cell: • Atoms in corners are ⅛ within the cell • Atoms on faces are ½ within the cell • Atoms on edges are ¼ within the cell

ATOMIC PACKING FACTOR • Fill a box with hard spheres - Packing factor = total volume of spheres in box / volume of box - Question: what is the maximum packing factor you can expect? • In crystalline materials: - Atomic packing factor = total volume of atoms in unit cell / volume of unit cell - (as unit cell repeats in space)

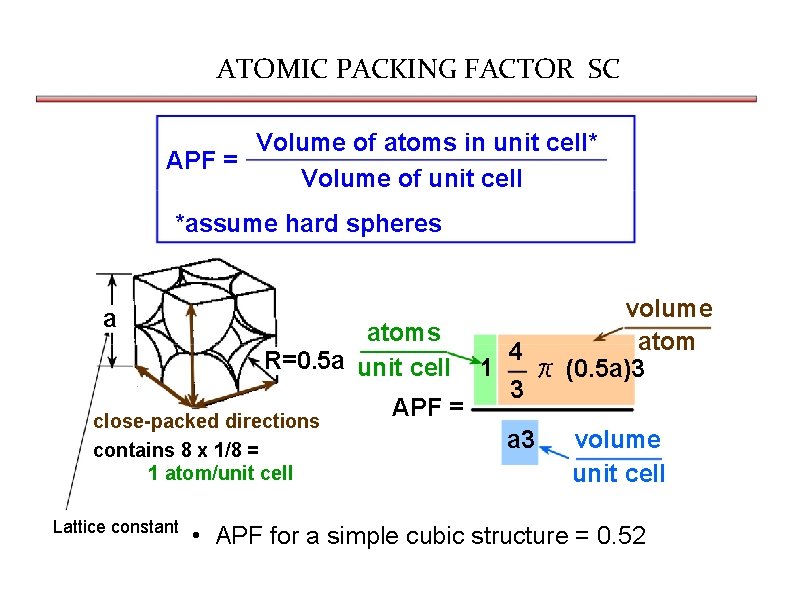
ATOMIC PACKING FACTOR SC Volume of atoms in unit cell* APF = Volume of unit cell *assume hard spheres a atoms R=0. 5 a unit cell close-packed directions contains 8 x 1/8 = 1 atom/unit cell Lattice constant APF = volume atom 4 1 π (0. 5 a)3 3 a 3 volume unit cell • APF for a simple cubic structure = 0. 52

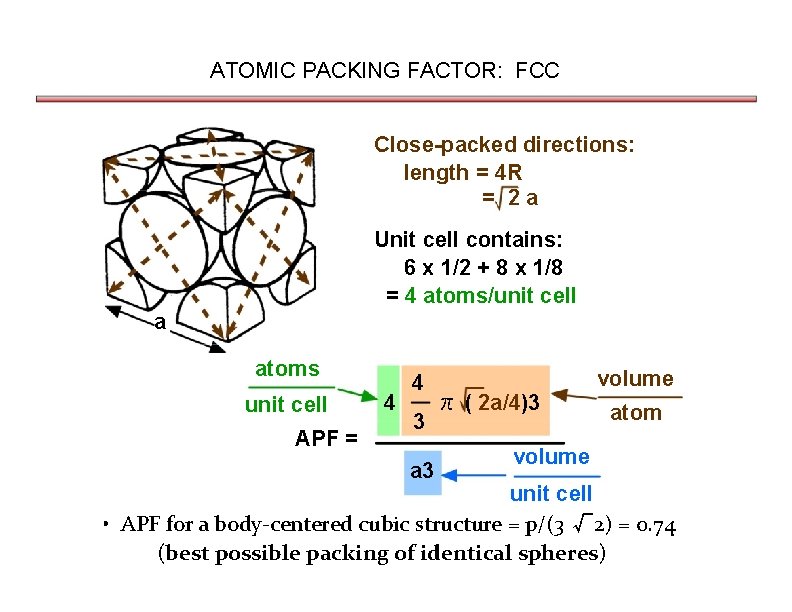
ATOMIC PACKING FACTOR: FCC Close-packed directions: length = 4 R = 2 a Unit cell contains: 6 x 1/2 + 8 x 1/8 = 4 atoms/unit cell a atoms unit cell APF = 4 4 3 a 3 π ( 2 a/4)3 volume atom volume unit cell • APF for a body-centered cubic structure = p/(3 √ 2) = 0. 74 (best possible packing of identical spheres)

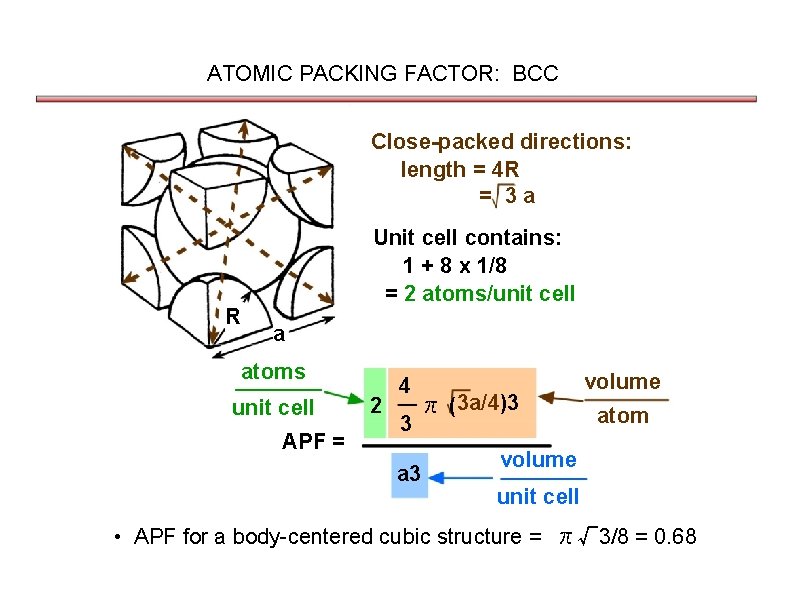
ATOMIC PACKING FACTOR: BCC Close-packed directions: length = 4 R = 3 a R Unit cell contains: 1 + 8 x 1/8 = 2 atoms/unit cell a atoms unit cell APF = 2 4 3 π ( 3 a/4)3 a 3 volume atom volume unit cell • APF for a body-centered cubic structure = π√ 3/8 = 0. 68

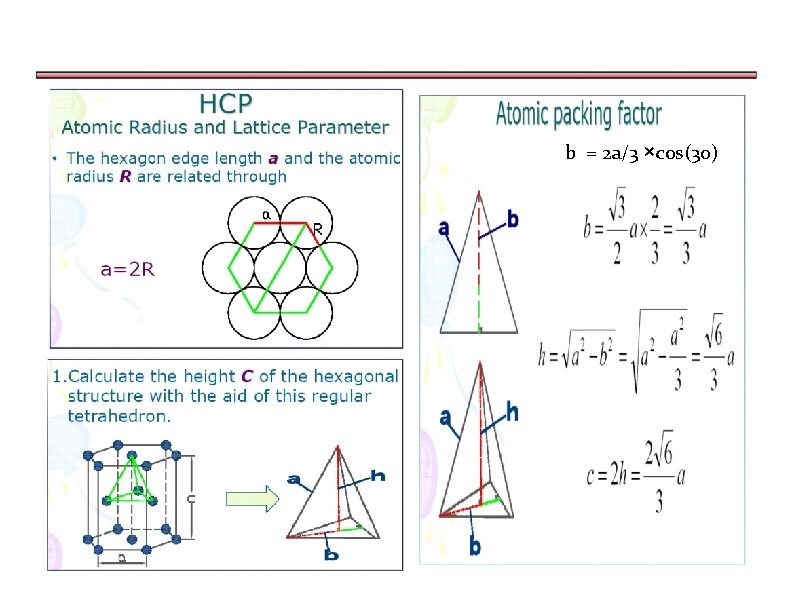
a)Calculating APF for Hexagonally closed packing structure

• Assumptions: To discuss crystalline structures it is useful to consider atoms as being hard spheres with well-defined radii. In this hard-sphere model, the shortest distance between two like atoms is one diameter of the hard sphere.

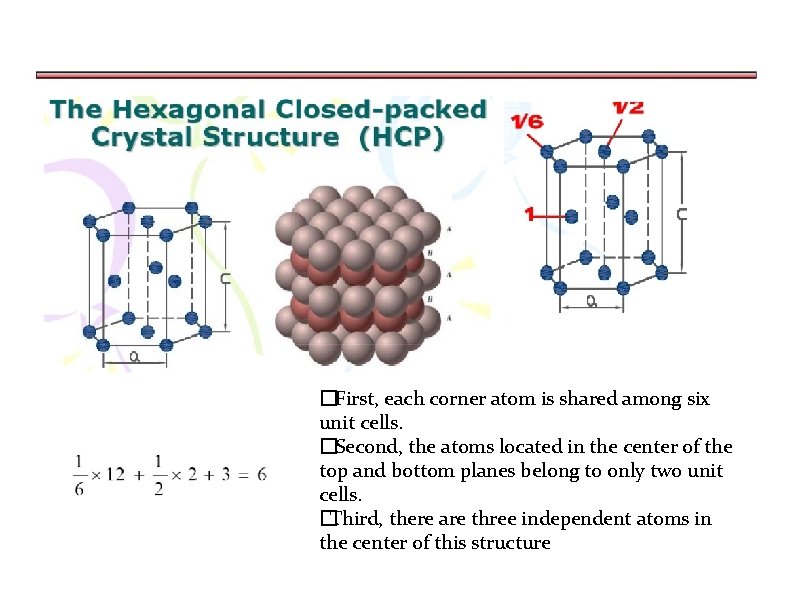
�First, each corner atom is shared among six unit cells. �Second, the atoms located in the center of the top and bottom planes belong to only two unit cells. �Third, there are three independent atoms in the center of this structure

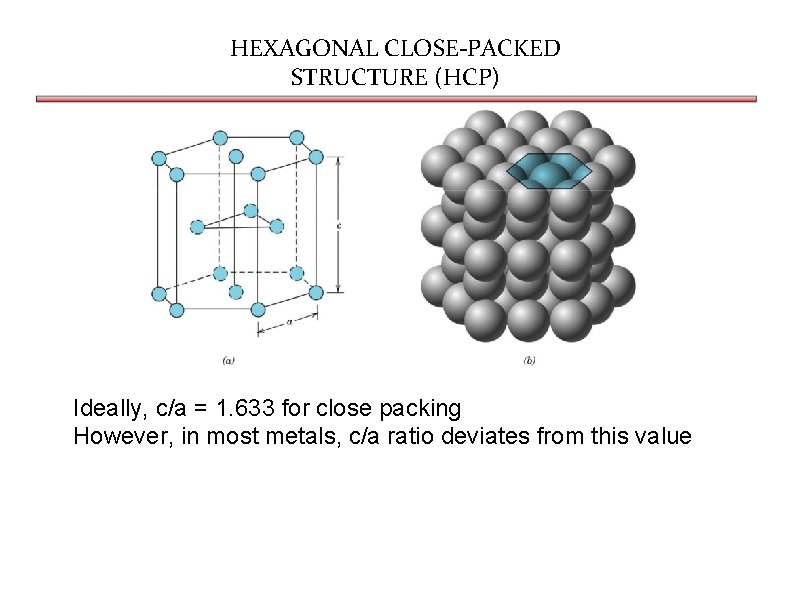
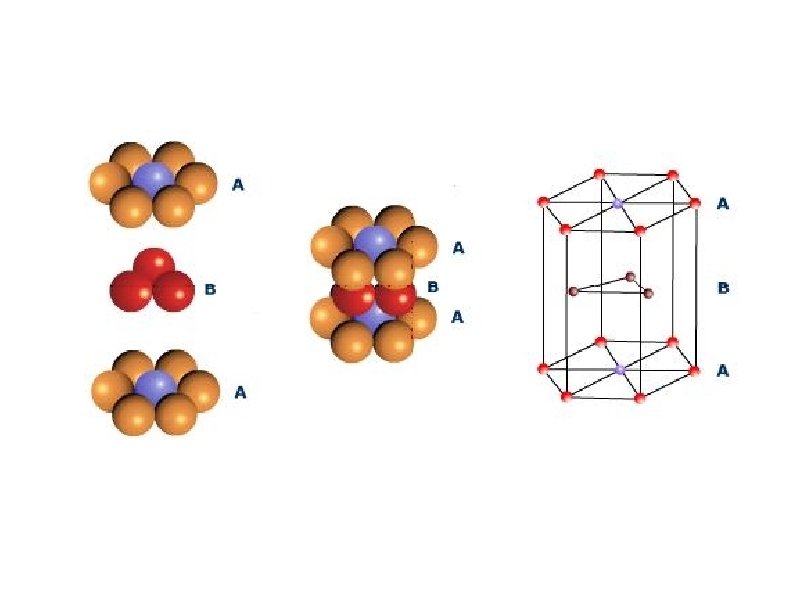
HEXAGONAL CLOSE-PACKED STRUCTURE (HCP) Ideally, c/a = 1. 633 for close packing However, in most metals, c/a ratio deviates from this value

b = 2 a/3 ×cos(30)

b)Calculating APF for Diamond structure

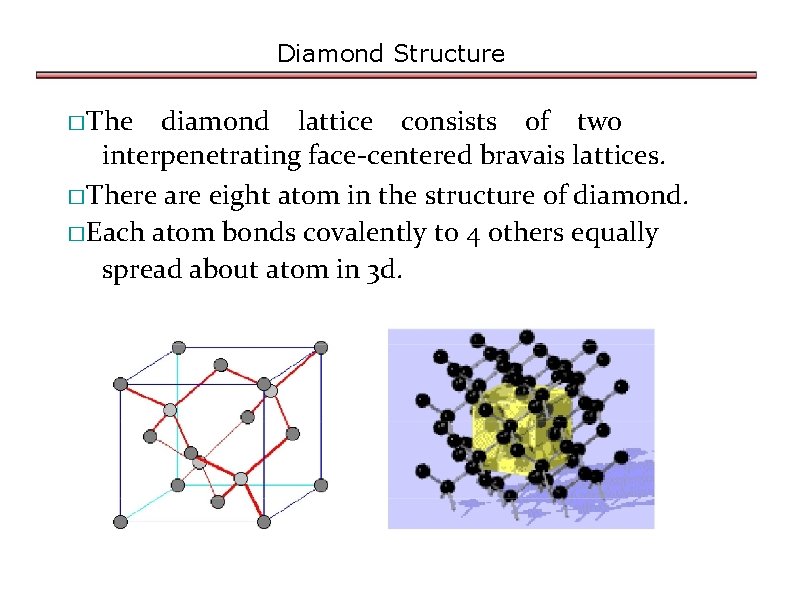
Diamond Structure �The diamond lattice consists of two interpenetrating face-centered bravais lattices. �There are eight atom in the structure of diamond. �Each atom bonds covalently to 4 others equally spread about atom in 3 d.

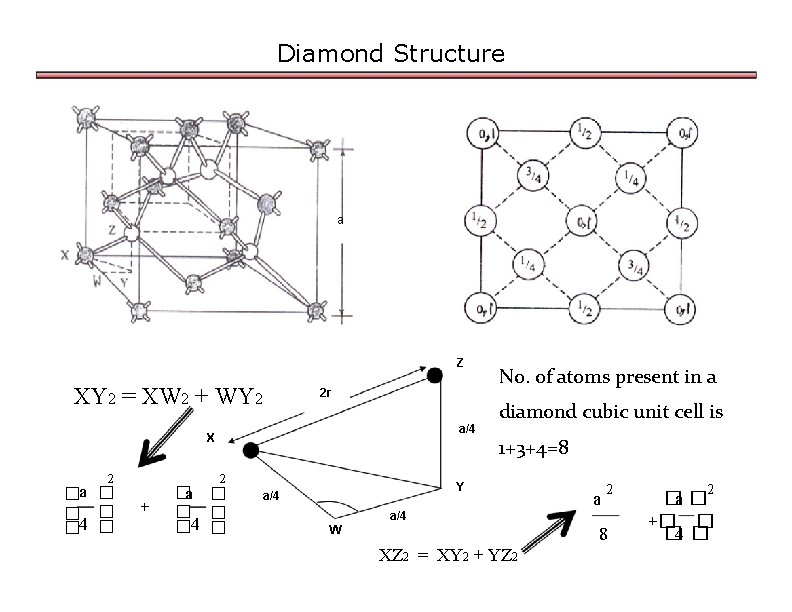
Some features � It is formed by carbon atoms � Every carbon atom is surrounded by four other carbon atoms (CN - 04) � situated at the corners of regular tetrahedral by the covalent linkages. � The diamond cubic structure is a combination of two interpenetrating FCC sub lattices displaced along the body diagonal of the cubic cell by 1/4 th length of that diagonal. � Thus the origins of two FCC sub lattices lie at (0, 0, 0) and (1/4, 1/4) �In diamond cubic unit cell there are 8 corner atoms, 6 face centered atoms and four other atoms

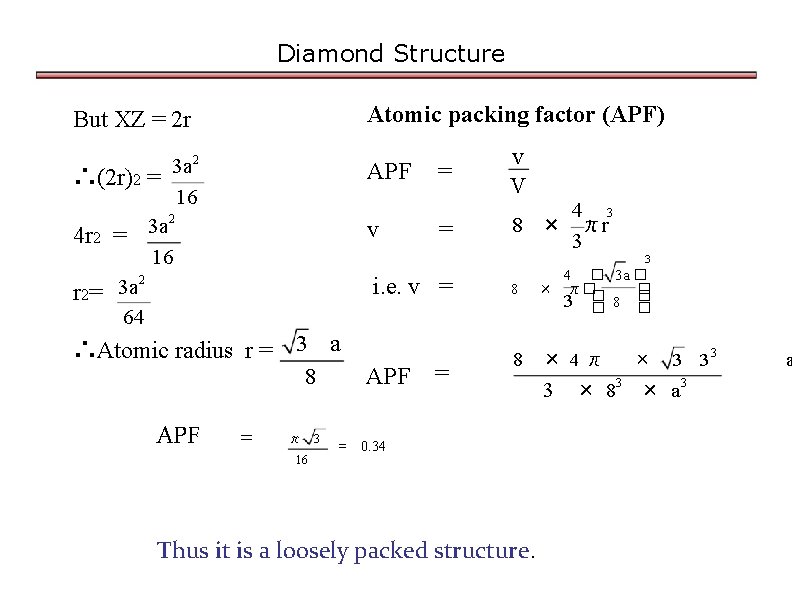
Diamond Structure a Z XY 2 = XW 2 + WY 2 2 r a/4 X 2 �a � � 4 � 2 + �a � � 4 � No. of atoms present in a diamond cubic unit cell is 1+3+4=8 Y a/4 a 2 a/4 W 8 XZ 2 = XY 2 + YZ 2 2 �a � +� � � 4 �

Diamond Structure But XZ = 2 r Atomic packing factor (APF) 3 a 2 ∴(2 r)2 = 16 2 3 a 4 r 2 = 16 2 3 a r 2= 64 APF v v V = 4 3 8 × πr 3 3 i. e. v = ∴Atomic radius r = 3 a 8 APF = = π 16 3 = APF = 8 4 � 3 a � × π�� � 3 � 8 � � 8 × 4π 0. 34 Thus it is a loosely packed structure. 3 × 8 3 33 × a 3 a

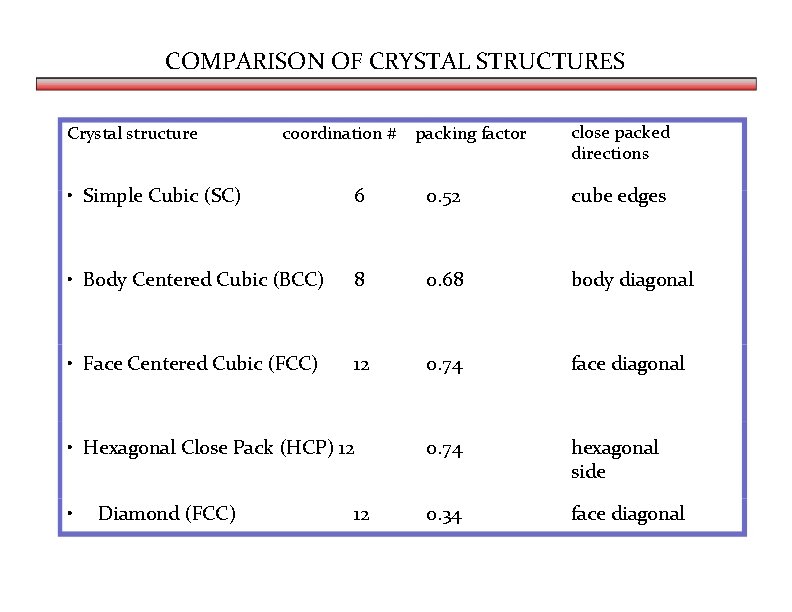
COMPARISON OF CRYSTAL STRUCTURES Crystal structure coordination # packing factor close packed directions • Simple Cubic (SC) 6 0. 52 cube edges • Body Centered Cubic (BCC) 8 0. 68 body diagonal • Face Centered Cubic (FCC) 12 0. 74 face diagonal • Hexagonal Close Pack (HCP) 12 0. 74 hexagonal side • 0. 34 face diagonal Diamond (FCC) 12

Lattice parameter of unit cell A unit cell can be constructed when we know distance between the two lattice points along three direction and angle between them The intercept made by edges of the unit cell along x, y and Z direction and interfacial angles are the lattice parameter of unit cell In this figure, a, b c and the angle α, β and γ is termed as lattice parameter Simple cube is a primitive cell as No. of atoms per unit cell is one BCC and FCC are non primitive. No. of atoms per unit cell is 2 and 4 respectively.

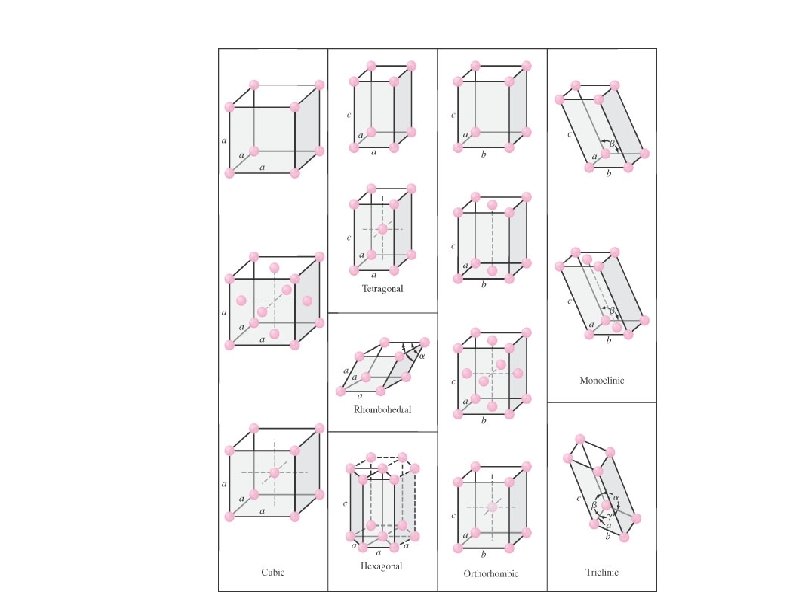
CRYSTAL SYSTEMS AND BRAVAIS LATTICES Seven crystal systems are each described by the shape of the unit cell which can be translated to fill space. Bravais lattices -- fourteen simple and complex lattices within the seven crystal systems.

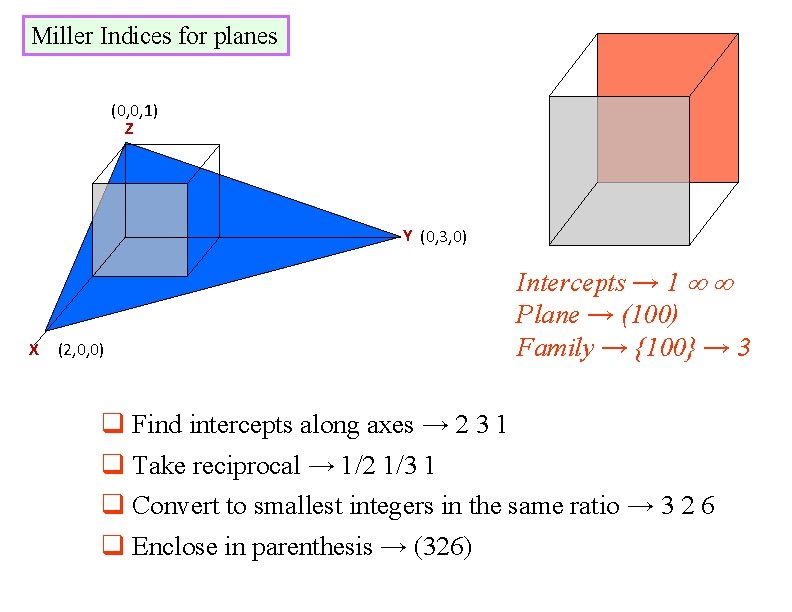
MILLER INDICES FOR CRYSTALLOGRAPHIC PLANES Definition: Miller Indices are the reciprocals of the fractional intercepts (with fractions cleared) which the plane makes with the crystallographic x, y, z axes of the three nonparallel edges of the cubic unit cell.

Miller Indices for planes (0, 0, 1) Z Y (0, 3, 0) X (2, 0, 0) Intercepts → 1 Plane → (100) Family → {100} → 3 q Find intercepts along axes → 2 3 1 q Take reciprocal → 1/2 1/3 1 q Convert to smallest integers in the same ratio → 3 2 6 q Enclose in parenthesis → (326)

D) Imperfections in solids

Ideal crystal- the atomic arrangement is perfectly regular and continous. But in real crystal due to some reason the arrangements of atom is disturbed along a point or along a line or in a region. The disturbance occured in the regular orientation of atoms is called a deffect Defects or imperfections thermodynamically • Defects in crystals cause distortion in the arrangement of atoms and subsequently can have tremendous effects on properties. are favoured

Dimensional Ranges for Different Classes of Defects a. Point defects (zero-dimensional) b. Line defects (single dimensional) c. Surface defects (two dimensional) d. Volume defects (three dimensional)

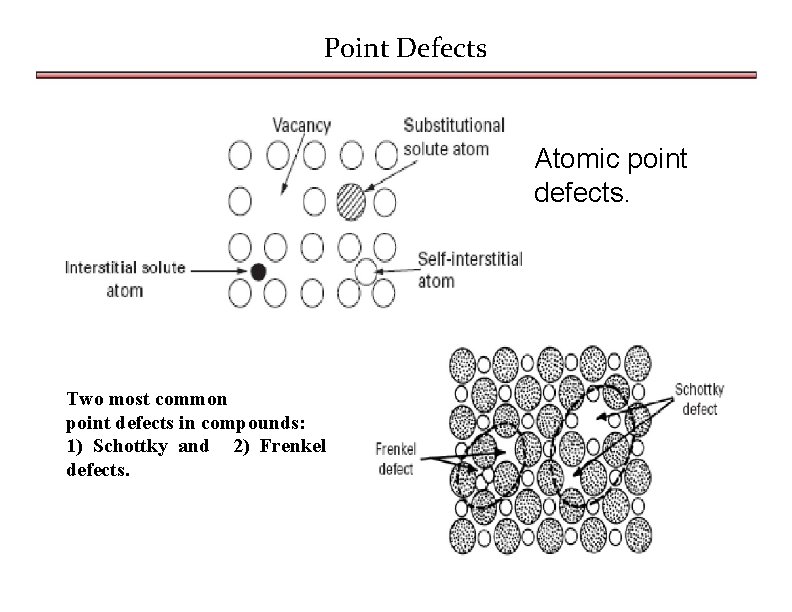
Point Defects Atomic point defects. Two most common point defects in compounds: 1) Schottky and 2) Frenkel defects.

Schematic depiction of various point defects -when an ion displaced from a regular position to an interstitial position creating a vacancy, the pair of vacancy-interstitial is called Frenkel defect. Cations are usually smaller and thus displaced easily than anions. Closed packed structures have fewer interstitials and displaced ions than vacancies because additional energy is required to force the atoms into the interstitial positions. - a pair of one cation and one anion can be missing from an ionic crystal, without violating the condition of charge neutrality when the valency of ions is equal. The pair of vacant sites, thus formed, is called Schottky defect. This type of point defect is dominant in alkali halides. These ion-pair vacancies, like single vacancies, facilitate atomic diffusion.

LINE IMPERFECTIONS (1 D defects) �The defects, which take place due to dislocation or distortion of atoms along a line, in some direction are called as ‘line defects ’. �Line defects are also called dislocations. In the geometric sense, they may be called as‘one dimensional defects’ �It may be ruptured at any place � Responsible for plastic deformations (slip). Two examples of line defects in nature: -A corn -Lines in a zebra

A comparison b/w regular and defect crystal

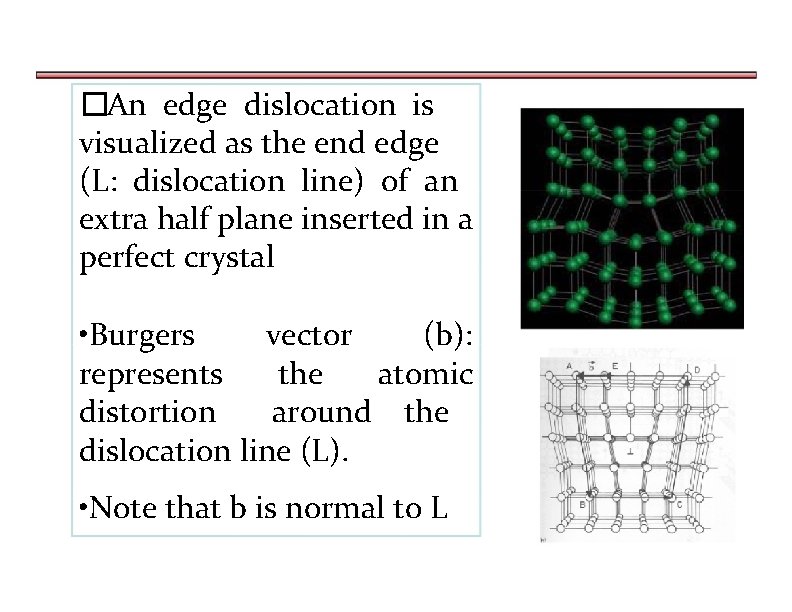
�An edge dislocation is visualized as the end edge (L: dislocation line) of an extra half plane inserted in a perfect crystal • Burgers vector (b): represents the atomic distortion around the dislocation line (L). • Note that b is normal to L

Burgers Vector • Burgers vector (b) defines the slip vector (slip magnitude and slip direction) • • To find Burgers vector, draw burgers circuit around a dislocation. • • The BV is the same along a dislocation line.

Screw dislocations -displacement of atoms in one part of crystal relative to rest. There is a line of atoms about which the crystals planes are twisted to give effect similar to thread Dislocation line

SURFACE IMPERFECTIONS The defects on the surface of material are called surface defects or plane defects Øgrain boundaries. Øtilt boundaries, Øtwin boundaries Østacking faults

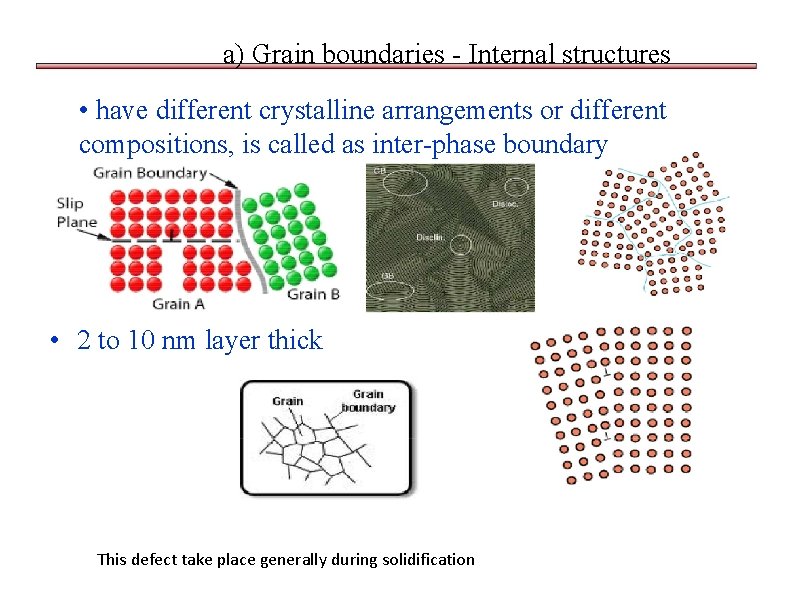
a) Grain boundaries - Internal structures • have different crystalline arrangements or different compositions, is called as inter-phase boundary • 2 to 10 nm layer thick This defect take place generally during solidification

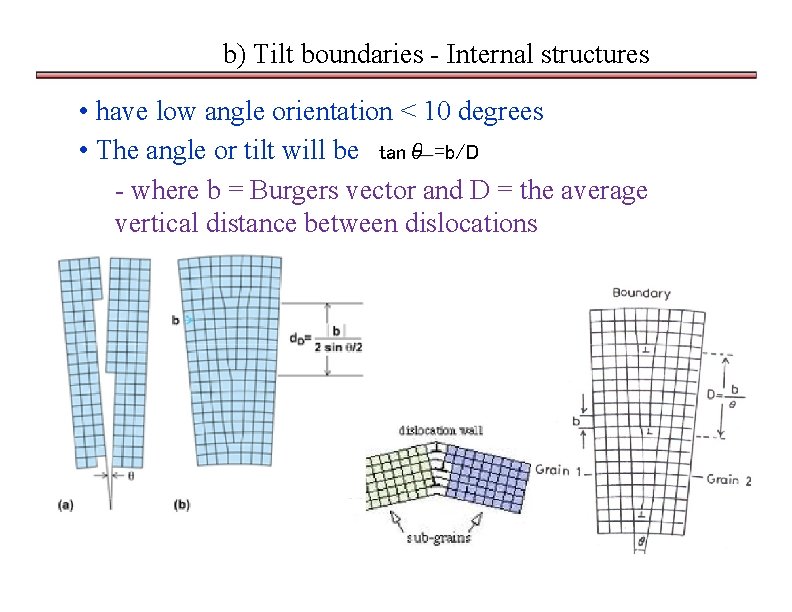
b) Tilt boundaries - Internal structures • have low angle orientation < 10 degrees • The angle or tilt will be tanθ =b/D - where b = Burgers vector and D = the average vertical distance between dislocations

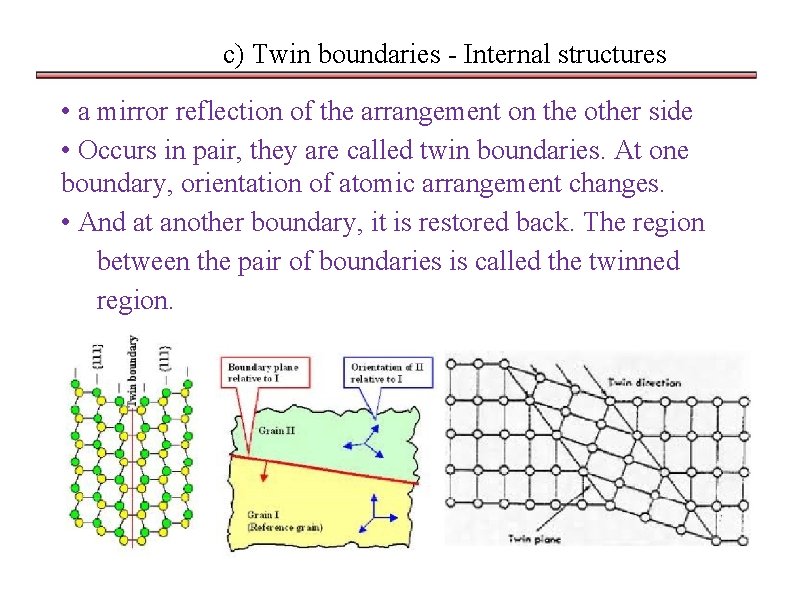
c) Twin boundaries - Internal structures • a mirror reflection of the arrangement on the other side • Occurs in pair, they are called twin boundaries. At one boundary, orientation of atomic arrangement changes. • And at another boundary, it is restored back. The region between the pair of boundaries is called the twinned region.

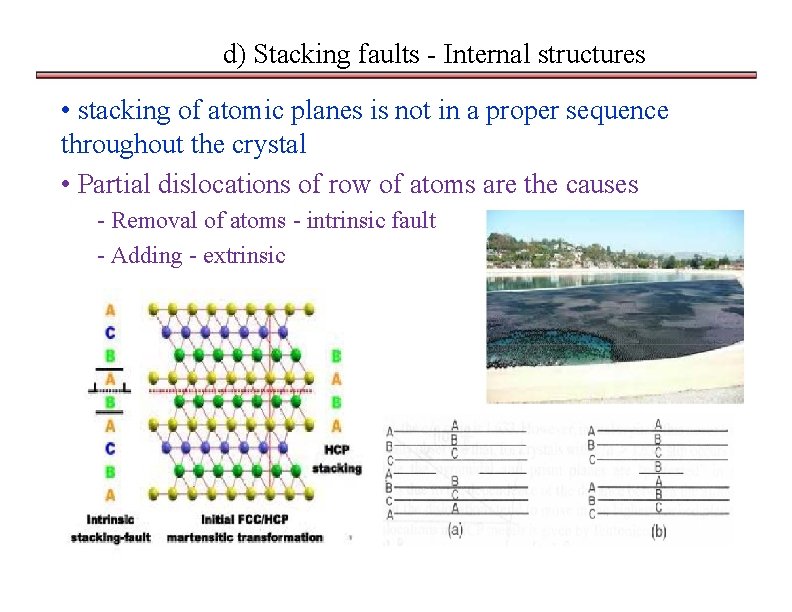
d) Stacking faults - Internal structures • stacking of atomic planes is not in a proper sequence throughout the crystal • Partial dislocations of row of atoms are the causes - Removal of atoms - intrinsic fault - Adding - extrinsic

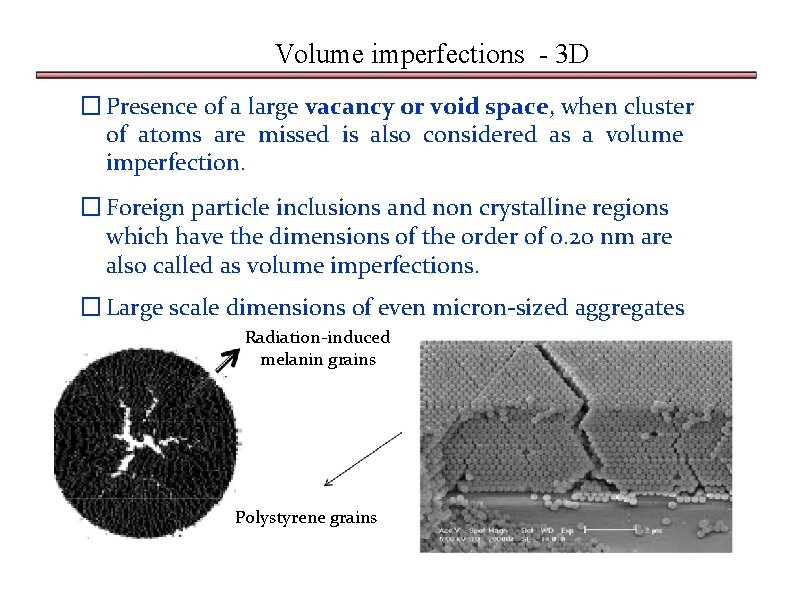
Volume imperfections - 3 D � Presence of a large vacancy or void space, when cluster of atoms are missed is also considered as a volume imperfection. � Foreign particle inclusions and non crystalline regions which have the dimensions of the order of 0. 20 nm are also called as volume imperfections. � Large scale dimensions of even micron-sized aggregates Radiation-induced melanin grains Polystyrene grains

C) Symmetry operations �Refers to internal atomic arrangement, �inherent property of crystals

ELEMENTS OF SYMMETRY Crystals have inherent symmetry- ordered arrangement of faces and edges Seven crystal System are characterised by 3 symmetry Elements v. Centre of Symmetry-Line drawn through it will meet surface of crystal at equal distance on either side. The point at body centre v. Plane of symmetry- When divided by imaginary plane into two halves such that one is mirror image of another v. Axis of symmetry-When crystal is rotated through it, the crystal remains invariant. The axis is called n fold axis if angle of rotation is 360/n.

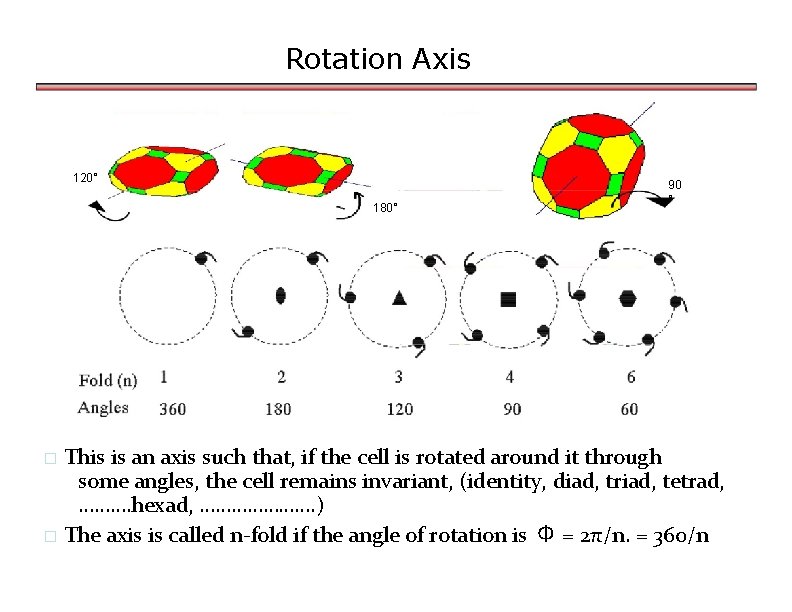
Rotation Axis 120° 180° 90 ° This is an axis such that, if the cell is rotated around it through some angles, the cell remains invariant, (identity, diad, triad, tetrad, ………. hexad, …………………. ) � The axis is called n-fold if the angle of rotation is Φ = 2π/n. = 360/n �

Cubic crystal does not possess any hexad axis. Crytsalline solid does not Show 5 -fold axis of symmetry. Quasicrystal ü ordered and no periodic arrangement. üIt forms pattern that fill the space but lack translational symmetry. üwhich means that shifted copy will not match its original

Rotation Symmetry We can not find a lattice that goes into itself under other rotations • A single molecule can have any degree of rotational symmetry, but an infinite periodic lattice - can not. Crystal Structure 38

Lattice goes into itself through Symmetry without translation Operation Element Inversion Point Reflection Plane Rotation Axis Rotoinversion Axes

Spacing between planes in a cubic crystal where dhkl = inter-planar spacing between planes with Miller indices h, k, and l. a = lattice constant (edge of the cube) h, k, l = Miller indices of cubic planes being considered.

Reciprocal lattice • If we assume a lattice with basis vector a, b and c • A new set of vector volume of unit cell = ῼ =a(bxc) v So, a*, b*, c* forms basis of new vector given by Gn= n 1 a*+n 2 b*+n 3 c* n 1, n 2 and n 3 are set of integers, a*, b*c* is reciprocal lattice and vector formed is called reciprocal basis vector Ø Important mathematical relation • a. a*=2π, a*. c= 0, a. *b=0

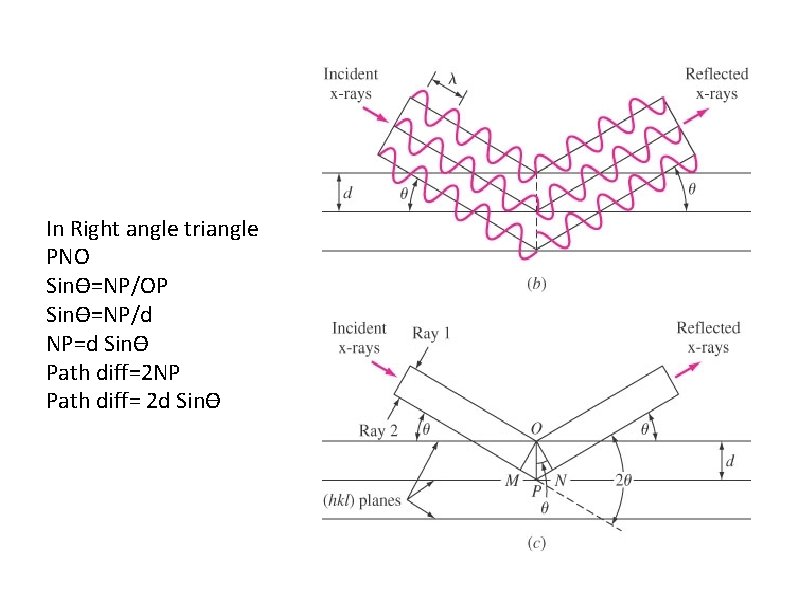
XRD • Bragg‘s law • Monochromatic X-ray Metal crystal Each atom acts as a source of scattering radiation of same wavelength and crystal acts as a series of paralled reflecting plane Intensity of relected beam is maximum when path diff between two reflected waves from different plane is an integral multiple of λ

In Right angle triangle PNO Sinϴ=NP/OP Sinϴ=NP/d NP=d Sinϴ Path diff=2 NP Path diff= 2 d Sinϴ

X-ray Diffraction and Braggs Law n = order of reflection, whole number of reflections λ = x-ray wavelength dhkl = spacing between planes with indices (hkl) θ = angle between incident x-ray beam and crystal planes (hkl)

For cubic crystals

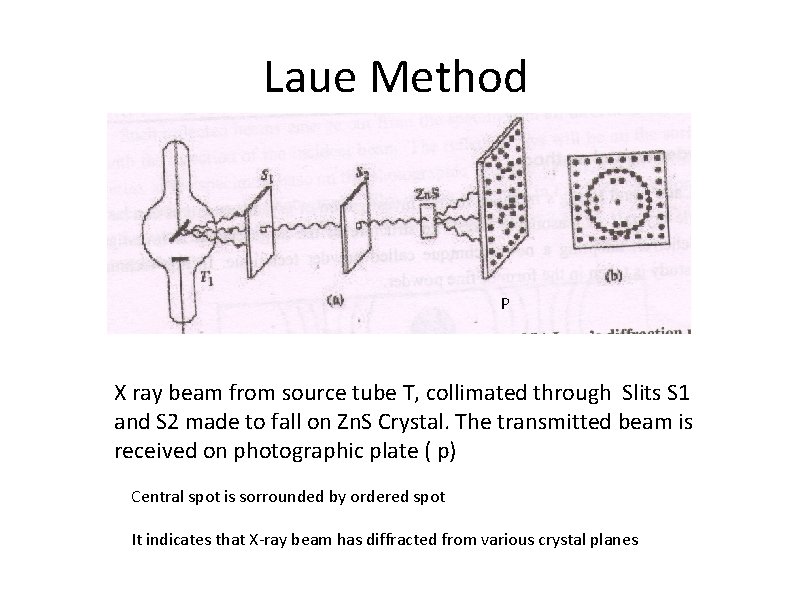
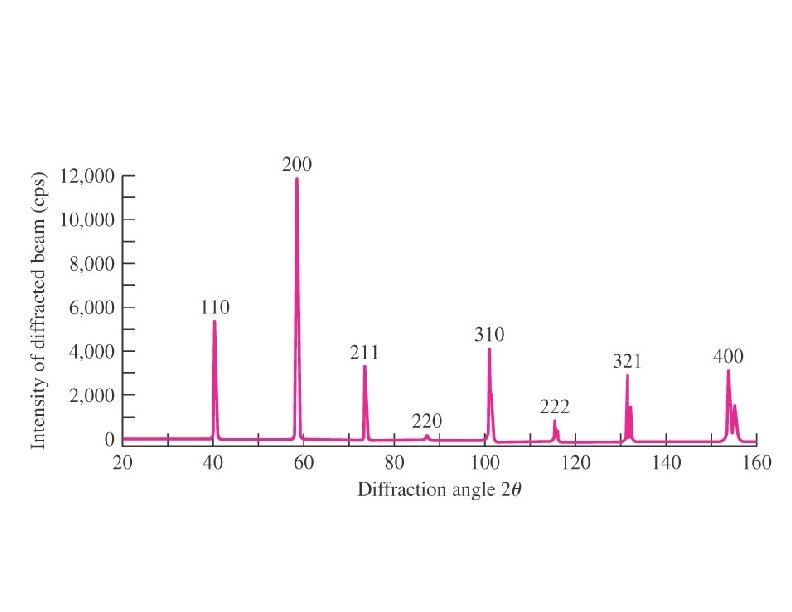
Laue Method P X ray beam from source tube T, collimated through Slits S 1 and S 2 made to fall on Zn. S Crystal. The transmitted beam is received on photographic plate ( p) Central spot is sorrounded by ordered spot It indicates that X-ray beam has diffracted from various crystal planes

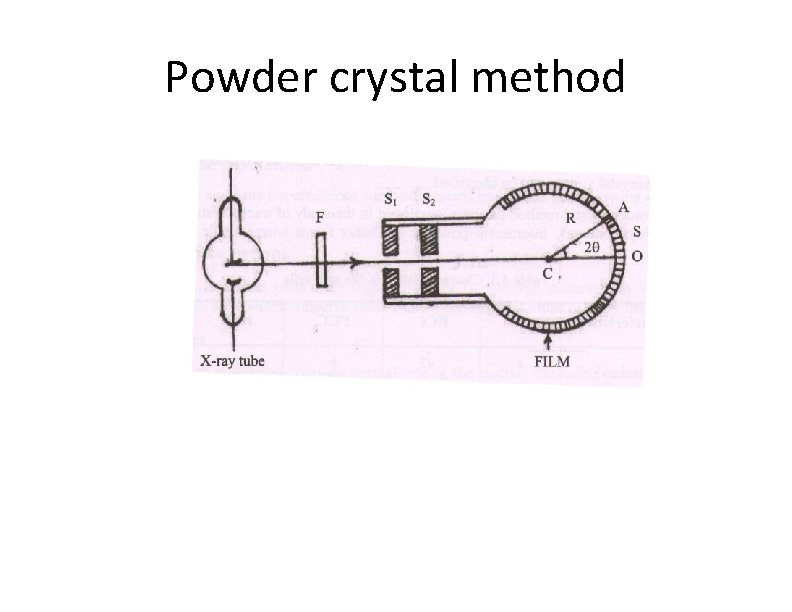
Powder crystal method