HOOKES LAW HOOKES LAW In the 1600 s

HOOKE’S LAW

HOOKE’S LAW In the 1600 s, a scientist called Robert Hooke discovered a law for elastic materials. Hooke's achievements were extraordinary - he made the first powerful microscope and wrote the first scientific best-seller, Micrographia. He even coined the word ‘Cell’.

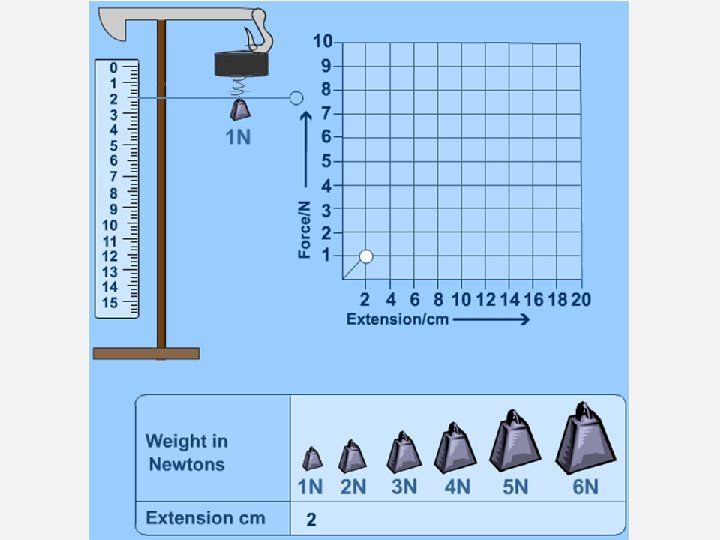
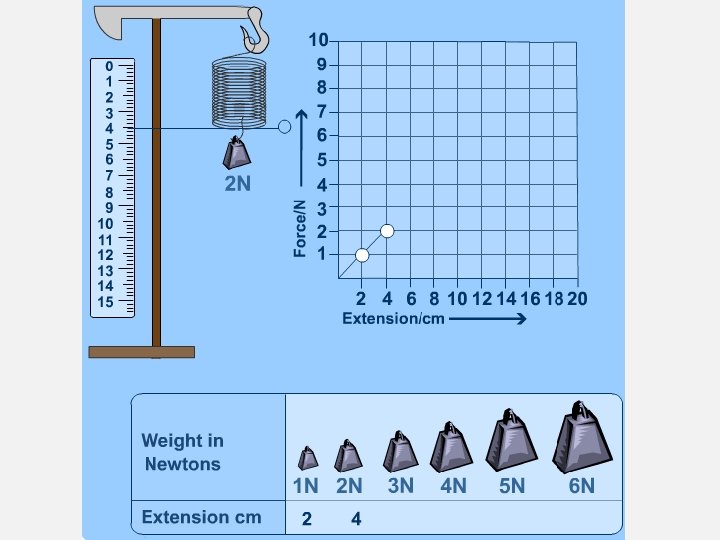
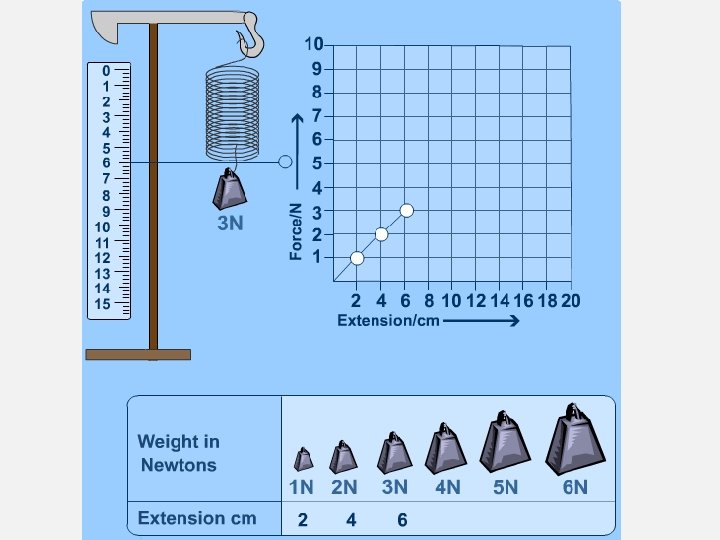
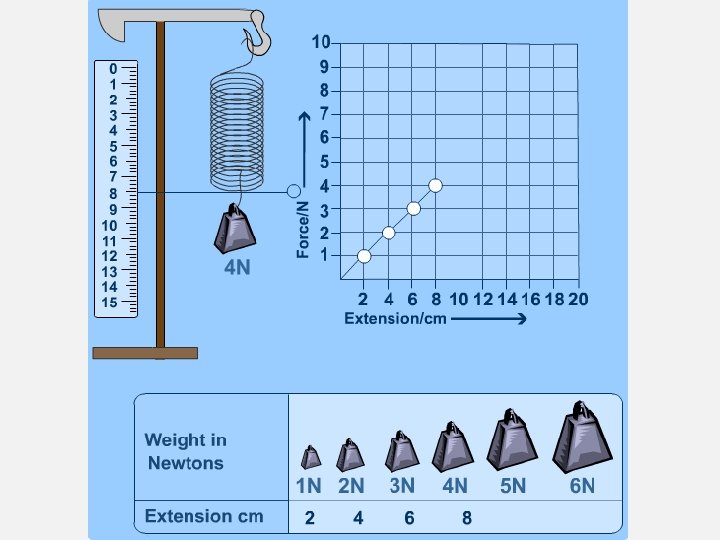
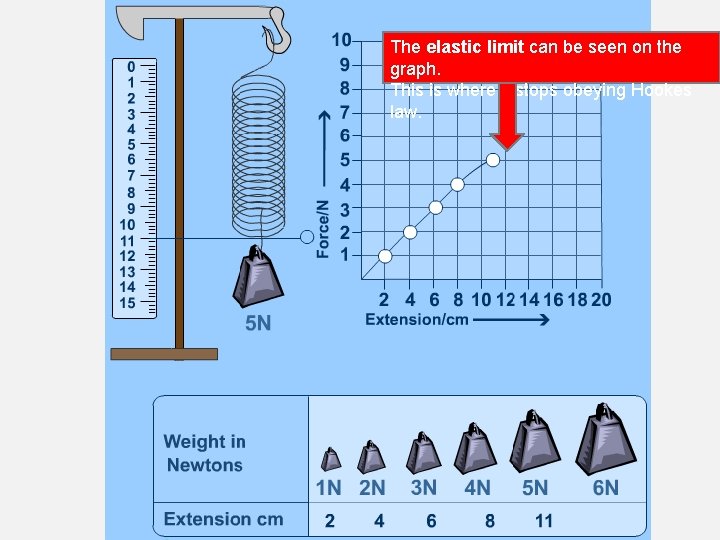
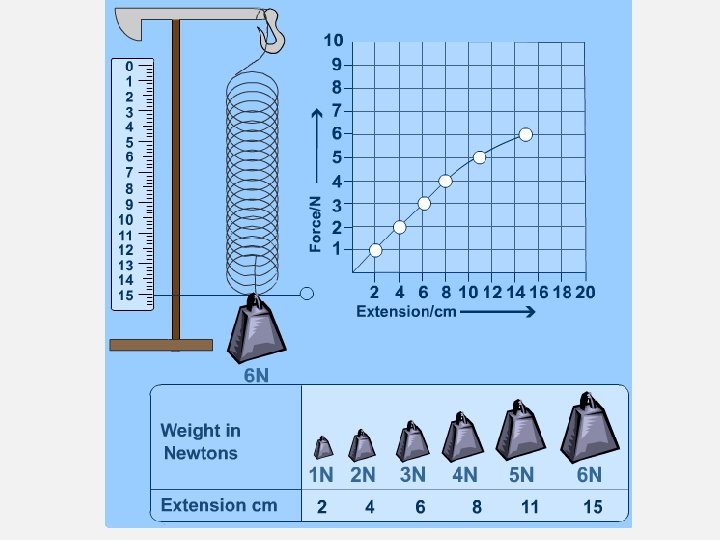
HOOKE'S LAW, ELASTIC AND PLASTIC BEHAVIOUR • If a material returns to its original size and shape when you remove the forces stretching or deforming it (reversible deformation), we say that the material is demonstrating elastic behaviour. • example is a spring • A plastic (or inelastic) material is one that stays deformed after you have taken the force away. If deformation remains (irreversible deformation) after the forces are removed then it is a sign of plastic behaviour. • example, crumpled paper • If you apply too big a force a material will lose its elasticity. • example, stretch a spring to far, break a hockey stick. • Hooke discovered that the amount a spring stretches is proportional to the amount of force applied to it. This means if you double the force its extension will double if you triple the force the extension will triple and so on.

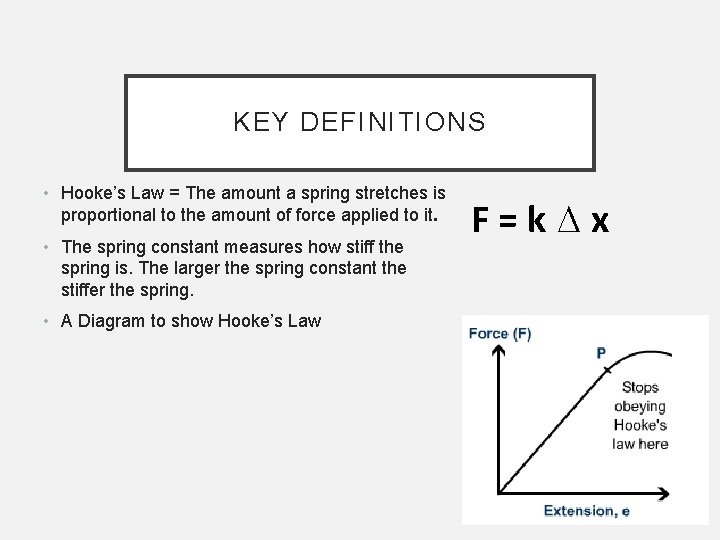
The elastic limit can be seen on the graph. This is where it stops obeying Hookes law.

HOOKE’S LAW Hooke's law: is a principle of physics that states that the force (F) needed to extend or compress a spring by some distance. F = k ∆ x Where: • F is the applied force (in newtons, N), • x is the extension (in metres, m) and • k is the spring constant (in N/m). • Recall ∆ is final change minus initial change.

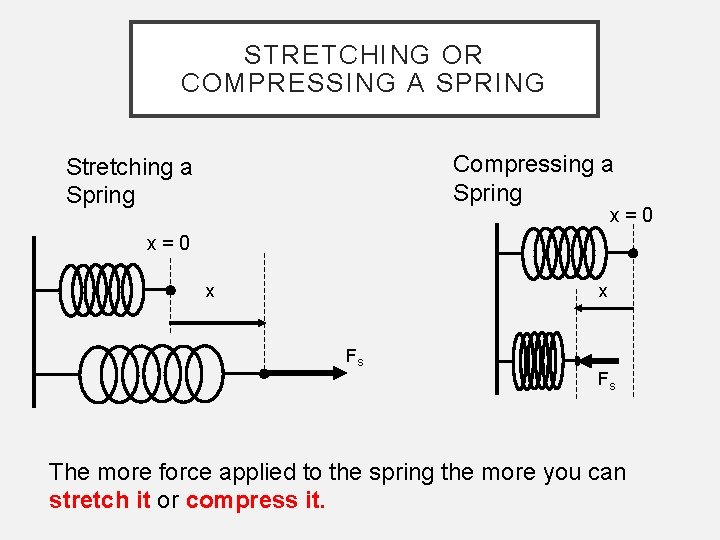
STRETCHING OR COMPRESSING A SPRING Compressing a Spring Stretching a Spring x = 0 x x Fs Fs The more force applied to the spring the more you can stretch it or compress it.

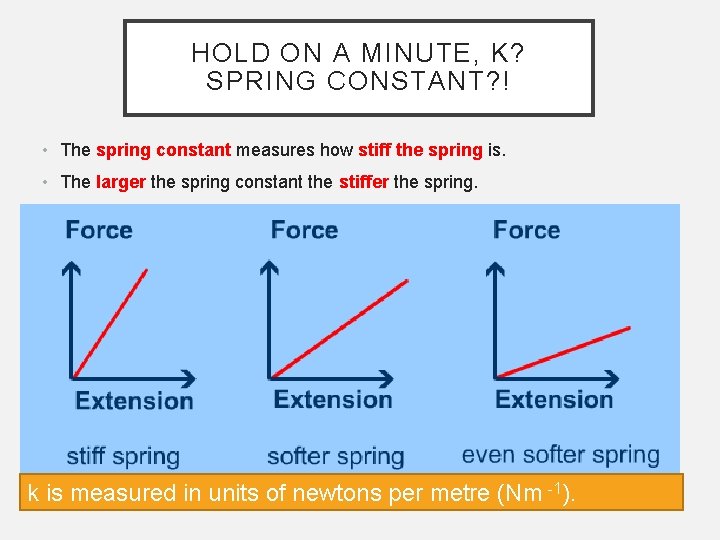
HOLD ON A MINUTE, K? SPRING CONSTANT? ! • The spring constant measures how stiff the spring is. • The larger the spring constant the stiffer the spring. k is measured in units of newtons per metre (Nm -1).

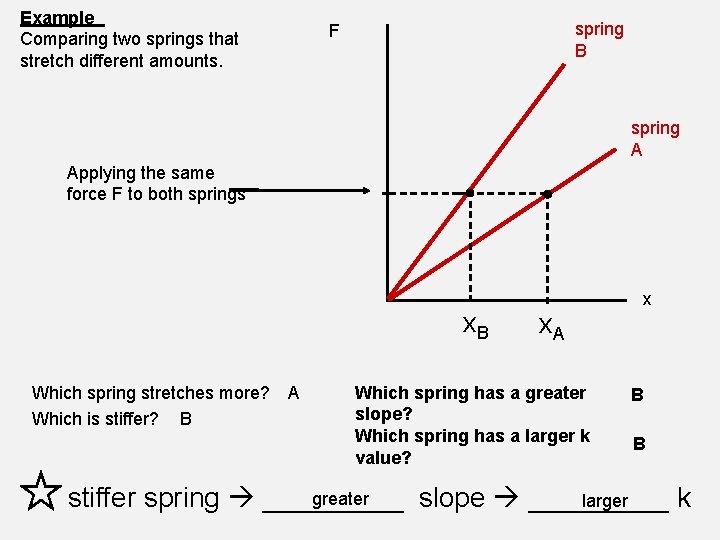
Example Comparing two springs that stretch different amounts. spring B F spring A Applying the same force F to both springs x. B Which spring stretches more? A Which is stiffer? B x. A Which spring has a greater slope? Which spring has a larger k value? x B B greater larger stiffer spring _____ slope _____ k

EXAMPLE #1 • A sack of potatoes is hanging from a spring. The potatoes weigh 56 N and their weight causes the spring to stretch 18 cm. What is the spring constant? • Known: 18 cm = 0. 18 m, and weight is 56 N • F=kx • 56=k(0. 18) • k= 311 N/m

EXAMPLE #2 • How much force is needed to stretch a spring 0. 25 m when it’s constant is 95 N/m? • F= 95 x 0. 25 = 23. 75 N (negative depending on the direction) • What is the spring constant when a 15 kg ham is hung on a spring that goes 20 cm? • Note: We had mass not weight!!! So 15 x 9. 8 = 147 N • 147=k(0. 2) so divide each side by 0. 2 and we get 735 N/m

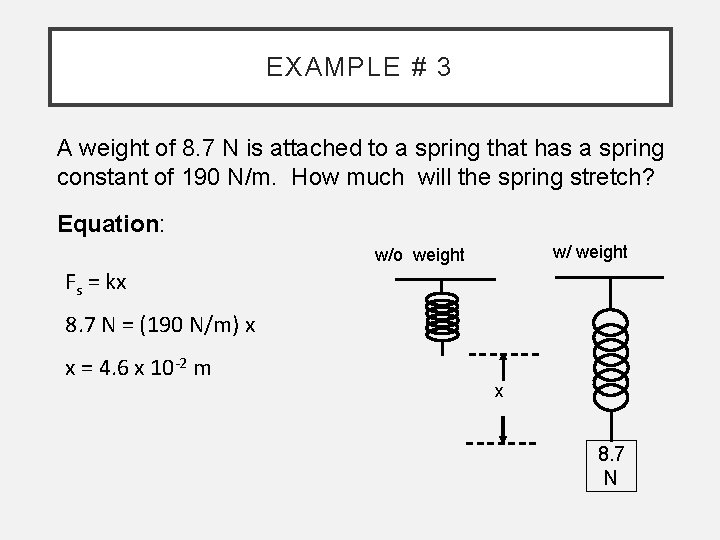
EXAMPLE # 3 A weight of 8. 7 N is attached to a spring that has a spring constant of 190 N/m. How much will the spring stretch? Equation: w/ weight w/o weight Fs = kx 8. 7 N = (190 N/m) x x = 4. 6 x 10 -2 m x 8. 7 N

EXAMPLE #4 • A spring is 0. 38 m long. When it is pulled by a force of 2. 0 N, it stretches to 0. 42 m. What is the spring constant? Assume the spring behaves elastically. Extension, ∆x = Stretched length – Original length = 0. 42 m – 0. 38 m = 0. 04 m F=k∆x 2. 0 N = k x 0. 04 m So, k = 2. 0 N 0. 04 m = 50 N m-1

EXAMPLE #5 Ex: A student stretches an elastic band with a spring constant of 50. 0 N/m by 15 cm. How much force are they applying?

EXAMPLE #6 • Ex: Al Mc. Innis uses a wooden stick with a spring constant of 850 N/m. What is the distortion on the stick if he exerts 525 N while taking a slapshot?

EXAMPLE #7 • A 65 kg girl sits in a human sling shot that has a spring constant of 10. 5 N/m. If the sling is stretched by 45 m, what is her initial acceleration when released?

KEY DEFINITIONS • Hooke’s Law = The amount a spring stretches is proportional to the amount of force applied to it. • The spring constant measures how stiff the spring is. The larger the spring constant the stiffer the spring. • A Diagram to show Hooke’s Law F=k∆x