Springs and Hookes Law Physics 11 Springs A

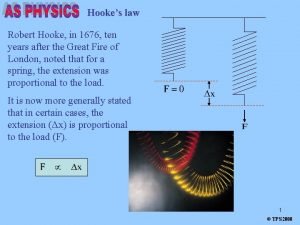
Springs and Hooke’s Law Physics 11

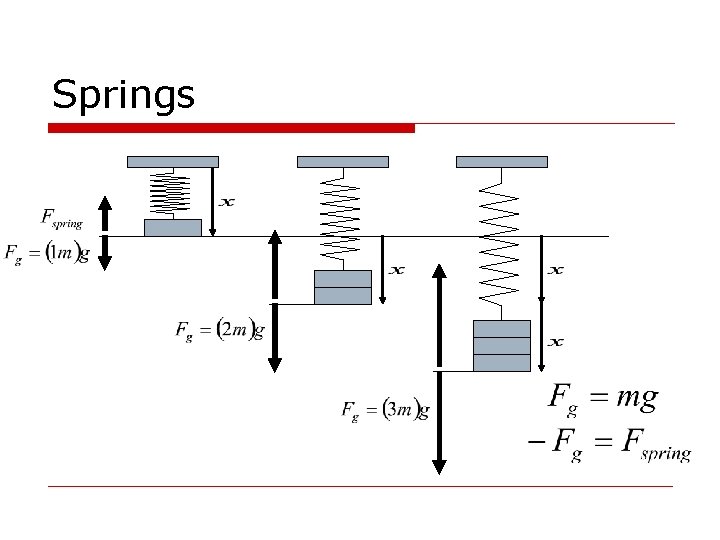
Springs A mass-spring system is given below. As mass is added to the end of the spring, how would you expect the spring to stretch?

Springs

Springs o o 2 times the mass results in a 2 times of the displacement from the equilibrium point… 3 time the mass… 3 times the displacement…

What kind of energy is this? o Potential Energy n Elastic Potential Energy to be exact!

What else besides springs has elastic potential energy? o o o Diving boards Bows (bow and arrows) Bungee cord

Hooke’s Law Fspring: Applied force X : displacement of the spring from the equilibrium position (units: m) K: the spring constant (units: N/m)

Hooke’s Law o the restoring force is opposite the applied force. (negative sign) n Gravity applied in the negative direction, the restoring force is in the positive direction

Example o An archery bow requires a force of 133 N to hold an arrow at “full draw” (pulled back 71 cm). Assuming that the bow obeys Hooke’s Law, what is its spring constant?

o o F = kx 133 = k(0. 71) k = 133/0. 71 k = 187. 32 N/m 190 N/m

Restoring Force o o The restoring force is the force that is needed to put the spring back to equilibrium. Example: If you stretch a spring by 0. 5 m and you had to use 150 N of force, the restoring force is -150 N.

Example 2: o A 70. kg person bungee jumps off a 50. m bridge with his ankles attached to a 15 m long bungee cord. Assume the person stops at the edge of the water and he is 2. 0 m tall, what is the force constant of the bungee cord?